基于ADAMS 的某客車動力總成懸置解耦設計

徐燚 龔光軍 陸昌年 魯磊

安徽職業技術學院 安徽省合肥市 230011

1 引言

現今路面條件已經得到了很大改善，而隨著各種汽車技術的發展和進步，汽車設計也正向著輕量化方向發展，汽車中最大振源因此成了發動機，這使得動力總成懸置隔振系統的性能設計顯得尤為重要。因此在其中的設計中，需要盡量追求懸置系統能夠具有較高的模態解耦程度，同時希望將其固有頻率盡量安排在較為合理的范圍內，這樣才能夠有效避免其以為有可能接近整車的其它模態頻率而產生共振現象。

2 動力總成懸置系統動力學模型建立

本文所研究的某客車使用了2.0T 渦輪增壓發動機及六擋手動變速器的動力總成，如圖1 所示。整個懸置系統的布置形式如圖2中所呈現的。本文研究的主要內容是動力總成懸置系統設計的一個重要方面，即實現Z軸的垂直振動以及繞X 軸振動模態的解耦。

圖1 動力總成示意圖

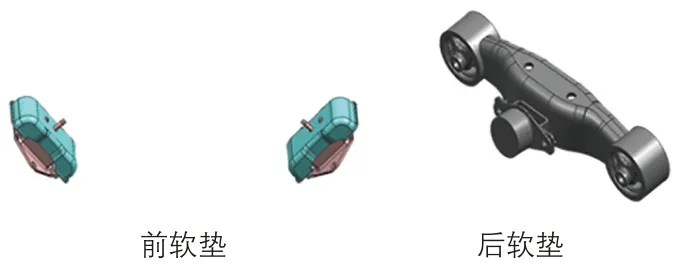
圖2 前后懸置模型示意圖

同時，本文中下面主要采用的部分解耦設計方法主要包括能量解耦法以及撞擊中心定理。

2.1 發動機總成動力學模型

相對發動機來說，我們認為橡膠軟墊因為彈性大所以是非常“軟”的，以此為前提可以把發動機動力總成簡化成剛體，同時，需要設置質量、質心、轉動慣量三個重要的參數，在本文中，動力總成質量參數已給定如下表所示：

2.2 懸置軟墊的動力學模型

在ADAMS 中建立模型時，橡膠墊是發動機和車架（“大地”）的連接，可以采用Bushing 建模，三個方向上的扭轉剛度為零，本文所采用的橡膠軟墊剛度標準參數已經給定如下：橡膠懸置X、Y、Z 方向的剛度分別為：后左：[44、111.4、292.8]；后右：[44、111.4、292.8]；左：[52.1、63.4、380.1]；右：[52.1、63.4、380.1]，單位N/mm。

2.3 在ADAMS 中建立懸置系統模型

在ADAMS 模型中建立懸置系統模型時需要始終按照一些方法和技巧來進行。由于本文中的該ADAMS 模型的要素主要是包括剛體、連接、激勵這三項，所以下面對這些要素相關的要點進行簡要敘述:

表1 動力總成質量參數

1）剛體：這里主要指的是發動機動力總成，它的繪制可以在ADAMS/View 中直接進行，同時認為它是一個具有6 個自由度的空間自由剛體。另外，客車的車架也是一個需要進行研究的對象，在這里，由于與整車相對比，發動機總成的質量是較小的，故而整個懸置系統可以直接拿出來進行單獨的討論和分析，同時可以用質量無限大的“大地”來代替車架；

2）連接：在本文中，該懸置系統采用了前二后一的布置形式（為了計算分析方便，將后懸置分解成兩個Bushing）。其中，前懸置的安裝角度為48°，后懸置的安裝角度為0°。懸置軟墊采用Bushing 建模，各方向的剛度前面已經給出；

3）激勵：分析懸置系統的固有特性時，可以暫時不必考慮激勵。

最終在ADAMS 中建立的動力總成懸置模型如圖3 所示：

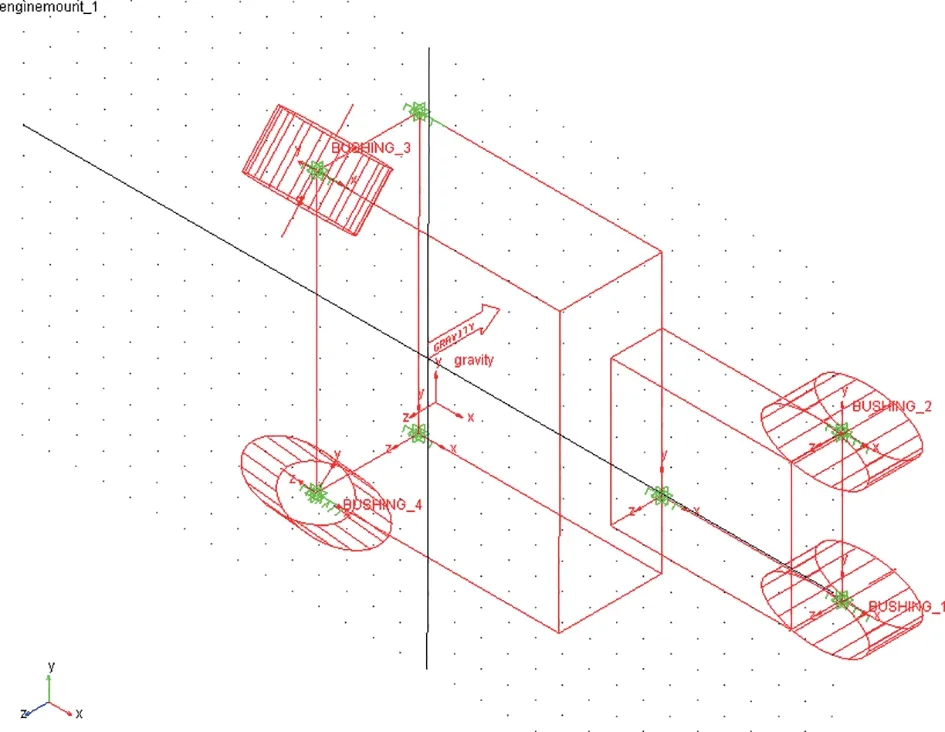
圖3 動力總成懸置系統的ADAMS 模型

3 懸置系統的固有特性分析

為了隔離發動機這個最大振源所產生的車體振動，經過分析得知，必須使得動力總成懸置系統具有優良的固有特性才能盡量減少這個影響。

3.1 固有特性的計算機仿真分析

在ADAMS/View 中 加 載 可 選 模塊ADAMS/Vibration， 菜 單 欄 中 出 現Vibration 菜單。在仿真計算時，為比較阻尼大小對系統固有特性的影響，故分兩種情況進行仿真計算，即有阻尼和無阻尼。

在經過ADAMS 仿真計算后，得出的計算結果，即主要包含動力總成懸置系統的無阻尼固有頻率如表2 所示：

表2 動力總成各階模態無阻尼固有頻率

各階主振型計算結果如圖4 所示：

在圖4 中，RX、RY、RZ 分別代表自由度α，β，γ，PART_3 為動力總成在ADAMS 中的實體名稱。

圖4 動力總成無阻尼主振型計算結果

得到各階振動的固有頻率以及主振型之后，可以計算出現有懸置系統在無阻尼的情況下各自由度的能量占系統總能量的比例，如表3 所示：

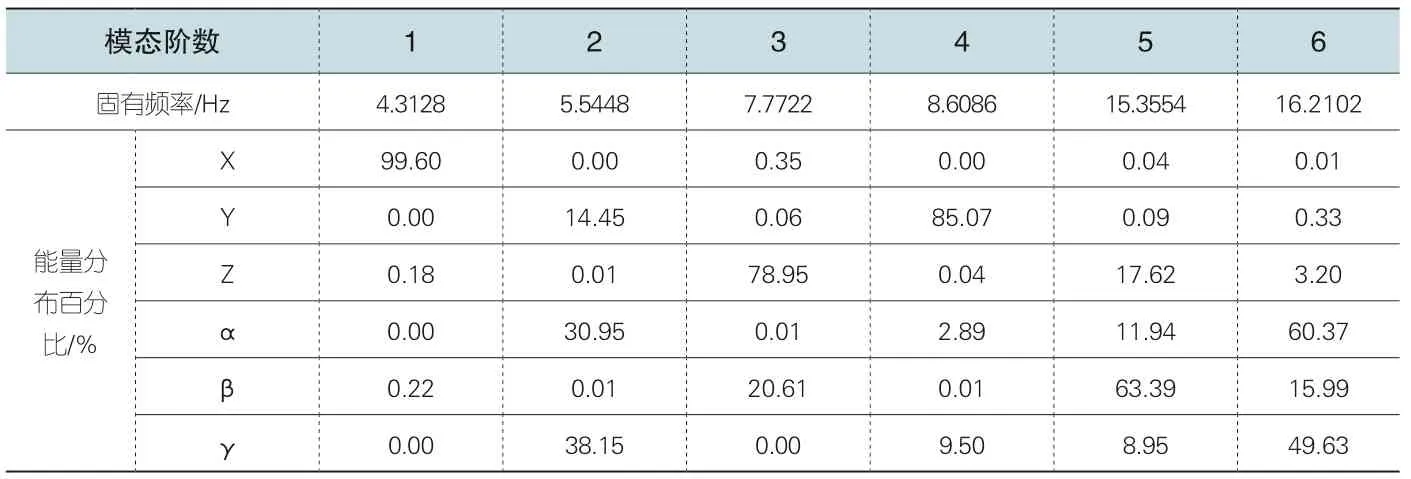
表3 無阻尼時各自由度能量分布

由于橡膠懸置阻尼很小，在未給定阻尼具體數值的情況下，將四個Bushing 的X、Y、Z 方向上的阻尼均設置為0.02N.s/mm 的小阻尼，對仿真計算的準確程度影響可以忽略。

在經過ADAMS 仿真計算后，得出的計算結果，即主要包含動力總成懸置系統的有阻尼固有頻率如表4 所示：

表4 動力總成各階模態有阻尼固有頻率

各階主振型計算結果如圖5 所示：

圖5 動力總成有阻尼主振型計算結果

在上圖中，RX、RY、RZ 分別代表自由度α，β，γ，PART_3 為動力總成在ADAMS 中的實體名稱。

得到各階振動的固有頻率以及主振型之后，可以計算出現有懸置系統在有阻尼的情況下各自由度的能量占系統總能量的比例，如表5 所示：

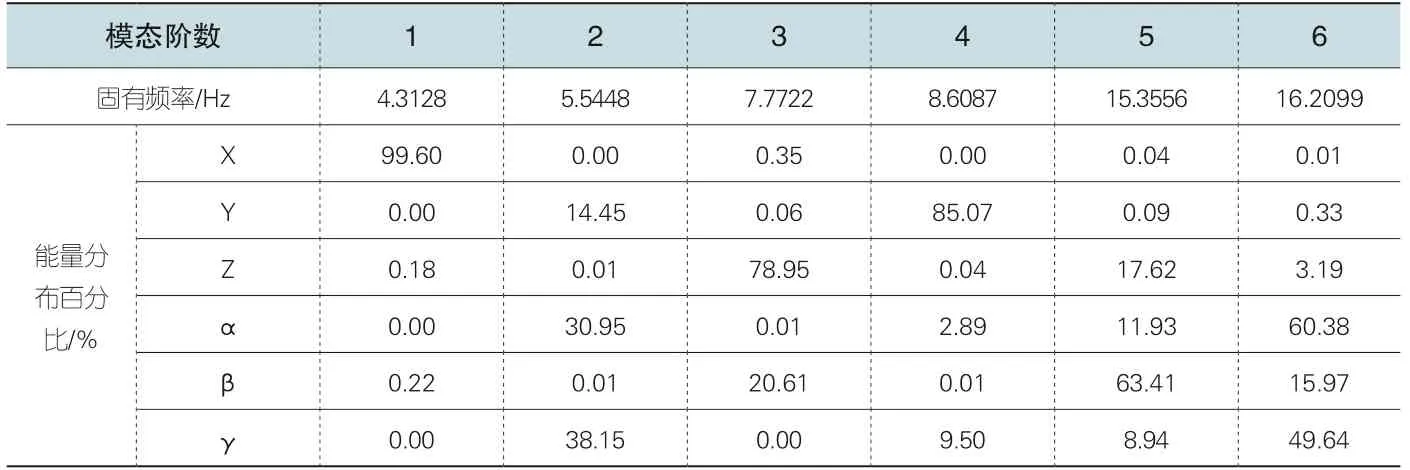
表5 有阻尼時各自由度能量分布

從以上的計算結果可以看出，各階模態均有一個比較突出的能量占優自由度；在無阻尼以及有阻尼的情況下均有二階模態、六階模態的振動耦合程度較高，其中尤其以二階模態為甚。該階模態的α、γ 自由度的振動能量分配僅相差7.2%，故需要進行解耦；而六階模態同樣也是α、γ 自由度的振動能量比較接近，相差10.74%，同樣也需要進行解耦。五階模態是一個非常復雜的耦合振動，雖然有明顯的振動占優方向，但是沿Z 軸上下平移的振動能量分配比例較大，而發動機激勵很容易引起Z 軸方向的垂直振動，故也需進行解耦，使β 自由度所占的能量盡可能比例擴大，已達到比較好的隔振效果。

對2.1.2、2.1.3 兩個小節所得出的分析結果進行比較可以知道，阻尼的大小對整個固有特性分析的結果影響很小，僅在高階振動時候對固有頻率和陣型有很小的影響，因此可以說明，懸置元件在簡化建模時可以簡化成無阻尼的三個正交彈簧即可。

4 懸置系統的解耦設計

在優化設計時，不改動原有懸置系統的布置形式。為了敘述方便，仍采用全文統一的參考坐標。

4.1 使用撞擊中心定理進行解耦設計

利用撞擊中心定理可以計算出前后懸置之間的距離，以判斷現有懸置系統是否符合撞擊中心定理的要求。根據前文所給出的動力總成質量參數的原始數據，動力總成的總質量為M=258.24kg，繞Y 軸的轉動慣量I=25.97kg·m，發動機前懸置到動力總成質心的距離L=650.99m,按撞擊中心定理計算，前后懸置之間的距離應為805.47mm，而現有懸置的前后距離為784.58mm，實際前后懸置的距離與根據撞擊中心定理計算得出的前后懸置距離僅相差20.89mm，可見，前后懸置之間的距離已經符合要求不需要再進行改動。

4.2 使用能量解耦法進行解耦設計

下面將對動力總成懸置系統虛擬樣機模型進行相應的參數化分析，分析中需要采用到的具體方法為ADAMS/View 中Optimization （優化分析）模塊。

可以設定DV_1 到DV_6 是四個懸置軟墊三個彈性主軸上的剛度變量；同理可得，可以設定只有兩個懸置安裝角度變量，即DV_7 和DV_8。綜上所述，模型中總共設定了DV_1 到DV_8 這8 個優化變量。

根據前面所得結論，本文中的優化目標主要是進行系統在沿Z與α方向上的能量解耦。

根據要求，采用無約束優化方法進行優化設計，因此不設定約束函數。

經過ADAMS 的優化計算，最終確定的優化結果如下：（1）四個懸置軟墊三個彈性主軸上的剛度分別為：左：[41.79 50.74 304.06]；右：[41.79 50.74 304.06]； 后 左：[35.2 89.15 234.19]；后右：[35.2 89.15 234.19]；（2）安裝角度為：前60°；后40°。

固有頻率如表6 所示：

表6 解耦設計后固有頻率

根據表中的數據，可以得出以下結論：在進行解耦優化設計后，系統的一至五階固有頻率降低明顯，這有助于進行隔振。值得注意的是，六階固有頻率有所上升，振型占優方向由α 變為γ，但發動機激勵主要集中在α 以及Z 方向，對方γ 向振動激勵并不是很大，因此，對整個系統的隔振影響不大。

解耦設計后各自由度的能量分布如表7所示：

根據表中的數據，可以得出以下結論：在進行解耦優化設計后，六階模態的振動耦合程度有所降低，振動占優方向的能量分布百分比有所增長；五階模態中，Z 方向的能量占有比例有所降低，對隔振有利；而二階模態仍舊耦合程度較高，盡管α 方向的能量占有率比原來有所降低，但是過寬的頻帶依舊容易引起共振，對隔振有所不利。

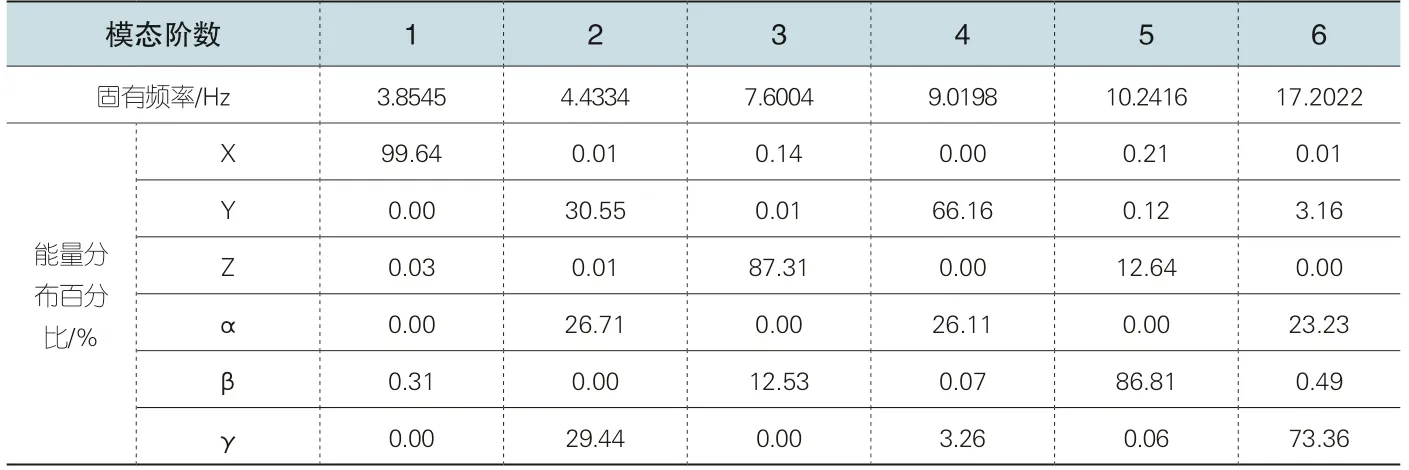
表7 解耦設計后各自由度能量分布

5 結論

在進行解耦優化設計后，系統的一至五階固有頻率降低明顯，這有助于進行隔振。同時，六階模態的振動耦合程度有所降低，振動占優方向的能量分布百分比有所增長；五階模態中，Z方向的能量占有比例有所降低，對隔振有利。