基于節約里程法的維修器材配送路徑設計
王金幗,王亞彬,王 帥,岳 帥
(陸軍工程大學石家莊校區,河北 石家莊 050003)
0 引言
維修器材保障是裝備保障工作的重要組成部分,近年來,日常訓練任務越來越重,裝備的使用消耗越來越大,損壞程度也越來越高,及時將維修器材配送到任務位置,可以保障裝備完好率。通過提高保障能力水平,能夠更好地發揮裝備的性能。器材配送運輸路徑的選擇是保障過程的一個關鍵性問題,運輸路徑選擇的優劣直接關乎到保障能力的好壞。因此只有選擇出合適的配送線路,才能使維修器材在最短的時間內,以最快的速度完成保障任務,使保障效益達到最大化。本文以尋求最短路徑為目標,通過最優維修器材配送路徑規劃,為維修器材配送提供可靠理論支撐。
1 模型構建
1.1 確定決策變量與建立模型。以某任務物資器材配送中心為例,如圖1 所示,配送中心為V,需要向8 個單位后方倉庫運送維修器材,分別記為V、V、V、V、V、V、V、V,構成配送網絡,其兩個節點分別記為i,j,其中決策變量是需要被選擇的節點之間 L(i=0,1,2,…,i;j=0,1,2,…,j)。配送中心現有載重量分別為50 噸、30 噸、10 噸的車輛各一輛可供使用,8 個后方倉庫V、V、V、V、V、V、V、V的需求量分別為:5、5、8、8、18、10、12、12 噸。

圖1 節約里程法示意圖
1.2 確定目標函數。假設從配送中心V出發,將維修器材運送到所有后方倉庫的道路為n 條,保證能夠滿足每個倉庫物資需求的同時,配送總里程為Dkm,求解最短里程minD。
1.3 尋找約束條件。維修器材需要配送到所有后方倉庫并滿足其需求量,在配送過程中,目的是能夠在現有條件下以最快的速度最短的距離將物資送達需求方,完成配送任務。此時不考慮道路情況以及載重對行車速度的影響。
2 模型的求解
通過對模型的分析,運用節約里程法對此模型的目標函數進行求解,步驟如下:

運用Dijkstra 算法,試探標號T 和永久標號P 和追蹤標號R。設V處為P(V)=0,其余節點均給T 標號,P(V)=+∞,比較所有具有T 標號的節點,把最小者改為P 標號,直到全部節點均為P 標號,則停止。根據圖1 匯總得出表1 各節點間最短距離表。

表1 各節點間最短距離 單位:公里
此時可以確定V到各個節點的最短路徑V、V、V、V、V、V、V、V分別為:VV—VV、VV—VV、VV—VV、VV—VV、VVV—VVV、VVV—VVV、VVV—VVV、VVVV—VVVV。
2.2 確定初始配送方案。根據表1 以及尋找到的由配送中心到各個后方倉庫的最短路徑可以得到配送的總里程數為:2×(22+24+24+36+47+46+48+61)=616km。共有8 條往返的配送路徑VV—VV、VV—VV、VV—VV、VV—VV、VVV—VVV、VVV—VVV、VVV—VVV、VVVV—VVVV。
2.3 計算節約里程。設兩節點分別為i,j,配送點之間節約的里程量為S,因此S=(V+V)-(ij)。根據表1,計算出節點的節約里程,結果如表2 所示。

表2 各節點節約里程 單位:公里
2.4 節約里程排序。根據表2,將節約里程按從大到小順序排列,如表3 所示。

表3 節約里程降序表 單位:公里
2.5 合并回路。節點VV節約里程最多,因此優先考慮VV兩點,構成一條回路:VVVVVVV,節約里程為:S(VV)=(VVVV+VVV)-ωVV=92km。共需運輸維修器材:47 噸,需要1 輛載重量為50 噸的車。此時配送節點中只剩V、V、V三個點,再由節約里程表中可得出V、V兩點可構成一條回路:VVVVV,節約里程為:S(VV)=(VV+VVV)-ωVV=34km。共需運輸維修器材:28 噸,需要1 輛載重量為30 噸的車。此時節點中只剩V節點,故VV節約里程0 公里。節約里程為:S(VV)=2VV-ωVV=0km。共需運輸維修器材:8 噸,需要1 輛載重量為10 噸的車。共節約里程126km。
2.6 重復合并。考慮節約里程第二的兩個節點VV,重復上述步驟,再次進行優化,以此類推,直到結果無變化,得到最終方案。
2.7 確定優化方案。經過上述分析,得出最終的方案可分為3條路線。路線1:VVVVVVV,總計里程136km;路線2:VVVVV,總計里程104km;路線3:VVV,總計里程72km。最終配送路線如圖2 所示。

圖2 最終配送路線
2.8 效率優化分析。根據圖2 得出最終配送路線優化方案,如表4 所示。
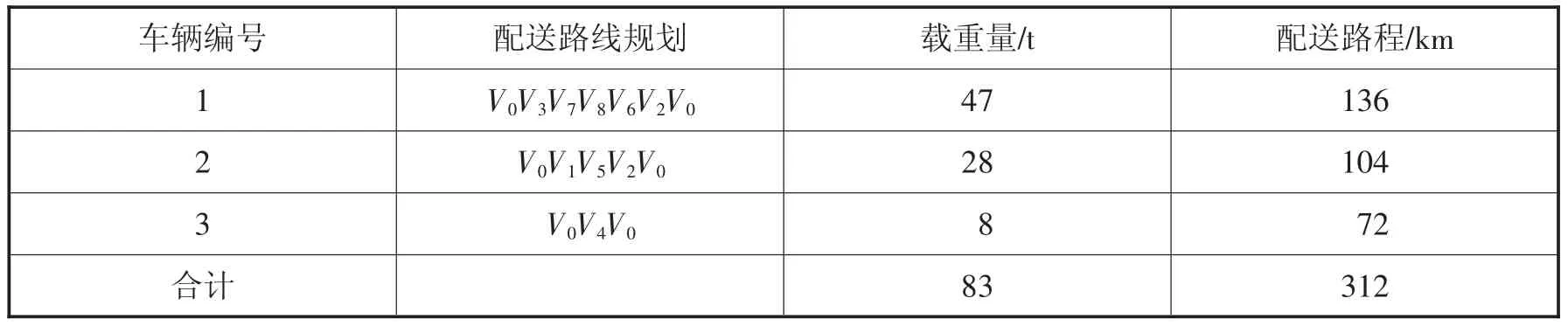
表4 最終配送方案
配送路程優化前,任務物資器材配送中心V到各個單位后方倉庫都采取一對一的配送方式,總配送里程為616km;而運用節約里程法在滿足載重量約束的前提下,優化后的總配送里程為312km,與最初配送方案相比共節約616-312=314km。優化后的配送路徑可以大大減少運輸所需成本,提高物資器材的配送效率,為后勤保障提供了有力支撐。
3 結束語
本文基于裝備保障背景,構造了一類維修器材配送數學模型。通過節約里程法,在滿足裝載約束的條件下最大程度縮減了運輸總距離,使配送距離最短的同時時間也達到最少,成本最低,計算出了最佳的配送路徑,達到了高效率配送效果。本文可為其他類似任務活動提供借鑒參考。
同時也存在一些不足,沒有考慮具體情況下的環境對道路的影響以及載重量不同對行車速度的影響等情況。下步的研究中將會重點考慮這些因素,不斷對模型進行優化,為特殊情況下提供更加可行的維修器材配送方案。

