多目標考慮下高超聲速進氣道唇口角參數化設計與分析

王翼，徐尚成，周蕓帆，范曉檣，王振國

國防科技大學 空天科學學院，長沙 410073

以超燃沖壓發動機為動力裝置的高超聲速飛行器近年來受到越來越廣泛的關注。作為沖壓發動機重要供氣部件，進氣道需在一定工作范圍內為燃燒室提供足量的高品質氣流。進氣道氣動性能和可靠性直接決定發動機性能和工作范圍，甚至關系到飛行器飛行速域。同時在一體化設計的要求下，進氣道產生的阻力應盡可能小。可以認為進氣道設計是在強幾何約束和氣動約束條件下的多目標優化設計問題。

典型高超聲速進氣道往往利用多級楔面或等熵壓縮曲面對氣流進行壓縮，然后通過唇罩將氣流捕獲進入內收縮段，并利用唇罩與壓縮側型面構成的收縮通道對氣流進行進一步壓縮。已有研究表明，唇罩形狀對進氣道性能有重要影響。常見的唇罩設計大致可分為2種思想：最小外阻思想和多級轉折思想。最小外阻思想設計下外罩與來流保持平行，唇罩通過單級壓縮將氣流轉為水平。這種設計可盡可能減小外罩阻力，在總轉角較小的進氣道構型中有明顯優勢。當外壓縮總轉角較大時，單級壓縮將形成過強的唇口激波，造成嚴重總壓損失。此時唇罩采用多級轉折思想設計，通過多道激波或一道唇口激波后接一系列壓縮波降低流動損失。Smart對具有多級楔角壓縮的二元超聲速進氣道展開研究。結果表明將唇罩由單級轉折變為二級轉折可有效減弱唇口激波強度，進而提高進氣道總壓恢復系數。張曉嘉等對典型二元高超聲速進氣道展開設計和分析，其唇罩采用單級壓縮。分析認為增大唇罩內型面角度可減弱唇口激波強度，從而減小內收縮段流動損失，但唇罩角度過大會產生較強烈唇口外激波，不利于飛行器減阻。綜合考慮，文中給出唇罩內角一般不大于4°。岳連捷等以發動機凈推力為主要優化目標對進氣道展開氣動優化。結果表明使凈推力最大的唇口角度對應的總壓恢復性能并非最佳。分析認為，盡管唇口角的設計使總壓恢復系數稍有下降，但唇罩阻力大幅減小，發動機性能反而得到提高。這些研究表明，唇口角設計中需綜合考慮進氣道氣動性能，才能提升發動機整體工作能力。

此外起動問題直接關系到進氣道穩定工作范圍，是進氣道設計中必須考慮的因素。Kantrowitz和Donaldson假設內收縮段入口處存在一道正激波，通過一維等熵流動計算得到進氣道臨界自起動的內收縮比(CR)。根據Kantrowitz準則，進氣道起動性能由內收縮比和來流馬赫數決定。然而大量數值仿真和實驗結果表明內收縮比大于Kantrowitz準則的進氣道也可實現起動。這主要是因為Kantrowitz假設進氣道入口處存在一道正激波，而實際進氣道入口處通過唇罩的設計產生斜激波，造成的流動損失偏小。Van Wie等在研究中發現唇罩長度、高度以及唇口角等幾何參數均對進氣道起動的臨界內收縮比有影響。Yue等通過風洞實驗開展唇口角對進氣道起動的影響及作用機理研究，發現唇口激波強度是決定進氣道起動性能的關鍵。基于此提出唇罩分級壓縮概念。Liu等基于簡化的二元高超聲速進氣道研究了唇口角對起動性能的影響，結果表明唇口角對進氣道性能有重要影響，使起動性能最佳的唇口角出現在4°。此外還發現不同唇口角下進氣道起動過程并不相同，其流動機理還有待深入研究。

高超聲速進氣道內收縮段設計狀態下包含多種激波波系、激波/邊界層干擾等流場結構，起動過程中還具有大尺度分離區結構。唇口角對設計條件下流場結構及進氣道起動過程有直接影響，但相關影響規律和流動機理還有待進一步開展。另外，從已有研究來看，唇口角對進氣道捕獲氣流品質、氣動力特性及工作范圍等均有重要影響。但目前對唇口角的研究大多只針對單一性能，未見有公開發表的文獻同時考慮包括總壓恢復性能、阻力特性和起動性能的唇口角設計相關研究工作。然而進氣道實際工作中需兼顧多種氣動性能，有必要開展多目標考慮下的唇口角設計工作。

本文以二維軸對稱高超聲速進氣道為研究對象，采用B樣條曲線對唇罩型線進行參數化設計。然后基于內收縮比為1.7的進氣道分別研究唇口角對進氣道總壓恢復性能、阻力性能和起動性能的影響規律，并從流動層面解釋其原因。接著研究不同內收縮比下唇口角對進氣道性能的影響規律，并在此基礎上綜合考慮總壓恢復性能、阻力特性和起動性能，探討多目標考慮下最優唇口角設計問題。

1 進氣道構型參數化設計方法

1.1 研究模型

圖1為高超聲速二維軸對稱進氣道構型，其中為軸向，為徑向，段為前體壁面，段為進氣道壓縮壁面。基于載荷考慮，該構型前體型面較長。在一體化設計要求下，前體壁面形狀保持不變，壓縮壁面在點處光滑過渡，并在喉部處保持水平。唇罩設計為環形，安裝于機身中部。進氣道總收縮比為6。考慮到真實條件下唇罩具有結構厚度，唇罩形狀由內型線和外型線確定。根據飛行器任務需求和發動機工作需要，設計狀態下進氣道以馬赫數()為5.4、攻 角為0°的狀態在高度為25 km高空(靜壓=2 511.02 Pa，靜溫=221.65 K)工作。

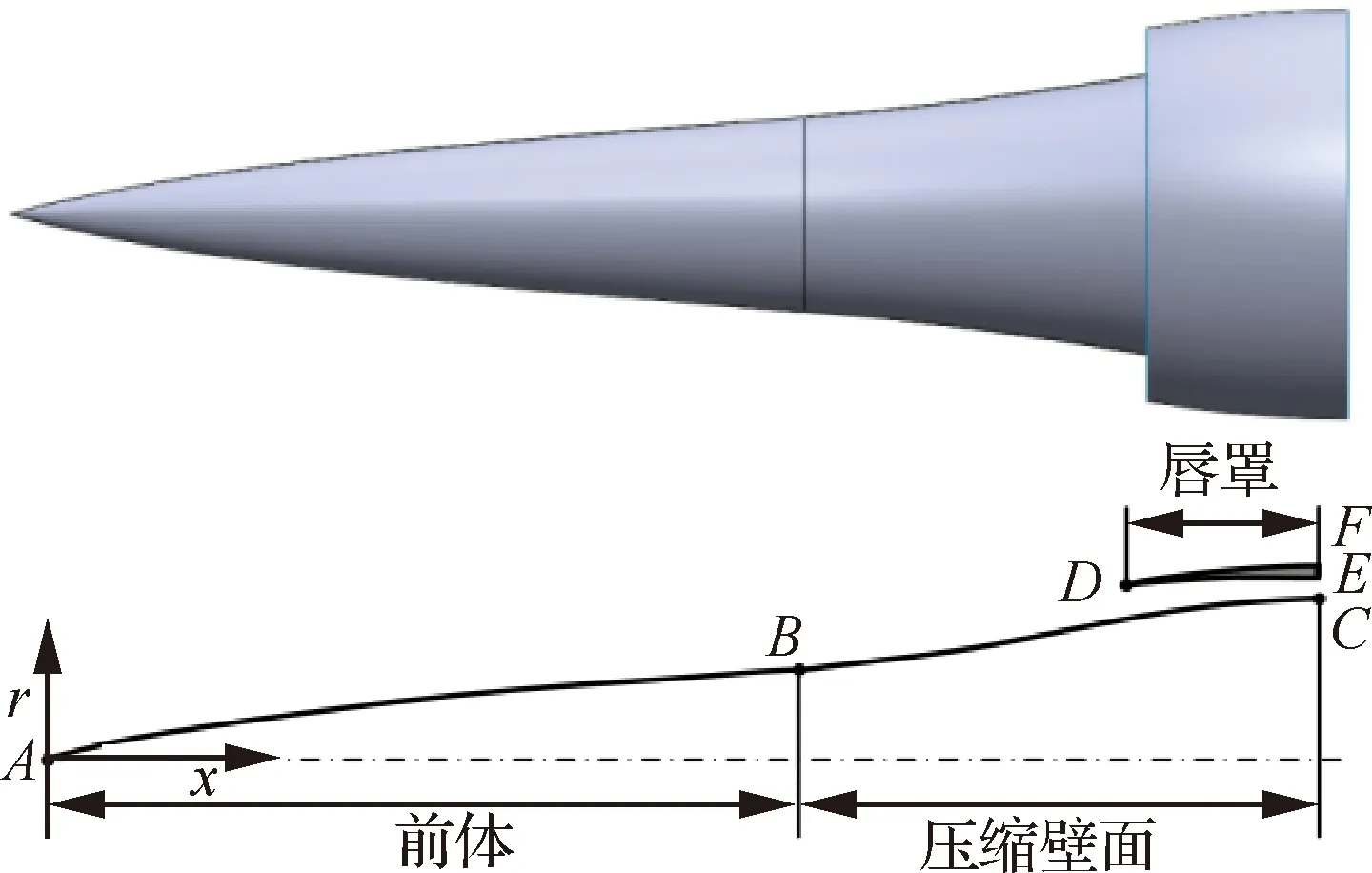
圖1 高超聲速二維軸對稱進氣道Fig.1 Two-dimensional axisymmetric hypersonic inlet

1.2 進氣道參數化設計

采用三階準均勻B樣條分別對唇罩內外型線展開參數化設計。B樣條曲線可通過調整控制點實現對曲線的局部控制，具有良好的靈活性。此外，B樣條方法生成的曲線起點和終點就是控制多邊形的起點和終點，并在起始和終止位置與控制多邊形相切。這些特點可使B樣條曲線在滿足一定幾何約束條件下實現對進氣道的幾何造型。

為滿足一體化設計需求，唇罩參數化設計需在一定的約束下進行。為保證流量捕獲需求，參數化設計中需保持唇口點位置不變。為實現進氣道與下游隔離段型面光滑過渡，需保證喉部位置和形狀不變，且唇罩內外型線在喉部處始終保持水平。基于結構和防熱考慮，唇口前緣處唇罩內外角之差取4°，唇罩在喉部處達到最大厚度。

圖2為唇罩內型線參數化設計示意圖。型線由4個點控制，其中為唇口前緣點，位于喉部，2點均為固定點，由此保證參數化設計中唇口前緣點和喉部位置始終不變。可沿與水平線呈角度的方向移動。與等高，可沿水平方向移動，從而使唇罩型線在喉部位置始終保持水平。4個控制點及其連線共同構成了控制多邊形。文中記至的距離為，至的距離為。由準均勻B樣條特點可知，曲線端點處角度與控制多邊形角度相同，因此在參數化設計中就是唇罩內角。通過調整、、的數值，可生成多種形狀的唇罩內型線。為簡化研究，取=200 mm，=100 mm，僅研究唇口角度對進氣道性能的影響。采用同樣的參數化方法可生成唇罩外型線構型，并保證喉部處唇罩厚度不變，唇罩內外角之差為4°。除特殊說明外，本文中所述唇口角均指唇罩內角。

圖2 唇罩內型線參數化設計方法示意圖Fig.2 Diagrams of parameterization method for inside cowl design

圖3為參數化設計得到的不同唇口角下唇罩

圖3 不同唇口角下進氣道唇罩型線對比Fig.3 Comparison of cowl configurations with different cowl lip angles

內外型線示意圖。可以看出唇口角對唇罩起始位置處的形狀有很大影響，曲線中部也有相應的變化。具體來說，唇口角越大，唇罩起始位置向外偏轉程度越大，唇罩型線整體向外凸起越多，但在流道后半部分唇罩內型線向下偏轉，流道快速收縮。唇口角較小時，唇罩在起始位置較平，而后緩慢向外偏轉。

圖4給出內收縮比為1.7、唇口角為4°時進氣道在設計條件下流場馬赫數云圖。氣流流經機體時，首先經過頭錐激波壓縮。由于前體型面較長，前體激波位于進氣道外側。而后氣流在前體壁面產生一系列膨脹波，流經壓縮壁面后氣流重新進行等熵壓縮。可以看出外壓縮壁面產生的第一道壓縮波打在唇口處，下游一系列壓縮波進入內收縮段，從而保證捕獲流量不受壓縮型面影響。最后氣流被唇罩捕獲至內收縮段進行進一步壓縮。

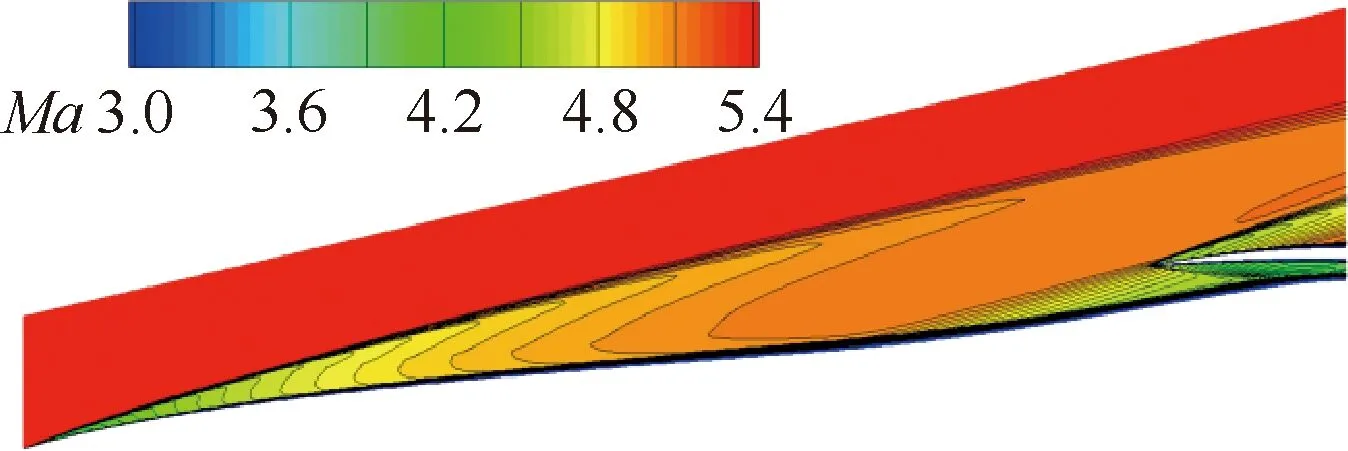
圖4 進氣道流場馬赫數云圖Fig.4 Mach number contour of inlet flow field

2 數值模型

2.1 計算方法

采用數值計算方法對本文研究的進氣道在設計點下的流場及加速自起動過程進行計算。采用有限體積法對Navier-Stokes方程進行空間離散，通量格式選擇AUSM (Advection Upstream Splitting Method)，對流項采用二階迎風格式進行求解。考慮到進氣道流場中有激波/邊界層干擾引起的分離流動，選擇對分離流有較好模擬能力的SST(Shear Stress Transport)-湍流模型。黏性流體采用Surtherland公式進行計算。

2.2 網格無關性分析和算例驗證

圖5為計算域網格劃分示意圖。由于模型具有二維軸對稱性，因此只計算二維流向流場。計算域入口設置為壓力遠場邊界條件。前體、壓縮壁面及內外唇罩均為無滑移壁面條件。計算域出口設置為壓力出口條件。網格設置中保證相鄰網格之間光滑過渡，盡可能保證網格正交，對氣流擾動較大的錐尖、唇口、進氣道內流道等位置進行加密。設置邊界層網格以盡可能準確模擬近壁低速流動，保證壁面大部分區域的在1以下。為保證計算結果精度的同時減小網格量，開展網格無關性研究。共設計3種網格規模，分別為疏網格(240×120)、中等網格(480×180)和密網格(720×240)。圖6為3種網格尺度下計算得到的壁面壓比分布，其中壓比采用自由來流靜壓無量綱化得到。3種網格設置均能準確計算流場中激波、激波/邊界層干擾等復雜流場結構引起的壓力變化。計算結果表明粗網格下進氣道總壓恢復系數與密網格相差2.85%，而中等網格下總壓恢復系數與密網格僅相差0.21%。此外，采用粗網格計算得到進氣道阻力系數為0.105 3，而中等網格和密網格下阻力系數分別為0.104 2、0.104 0。這表明隨著網格量的增加，進氣道氣動參數逐漸收斂。最終考慮到計算量和計算精度，選擇中等網格展開后續數值計算。

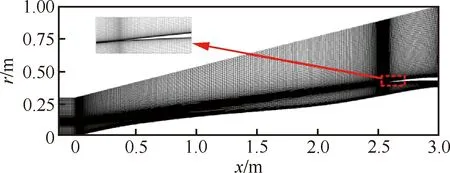
圖5 計算域及網格劃分示意圖Fig.5 Diagrams of computational domain and grids

圖6 不同網格下進氣道壁面沿程壓力對比Fig.6 Comparison of wall pressure with different grid scales

為驗證本文數值計算方法對進氣道內流場結構模擬的準確性，采用文獻[21]的進氣道試驗結果進行算例驗證。圖7為實驗紋影圖像和采用本文網格劃分策略、數值計算方法得到的數值紋影結果。圖8為實驗和數值計算下壁面壓力分布對比圖，其中為風洞噴管出口靜壓。由圖7和圖8可知數值仿真得到的流場結構及壁面壓力分布與實驗結果基本相同。這表明本文采用的計算方法可較好地捕捉進氣道流場內部波系結構，保證了本文數值方法對計算進氣道內流動的可靠性。

圖7 進氣道實驗和數值計算下流場紋影對比Fig.7 Comparison of schlierens between current simulation and experimental data

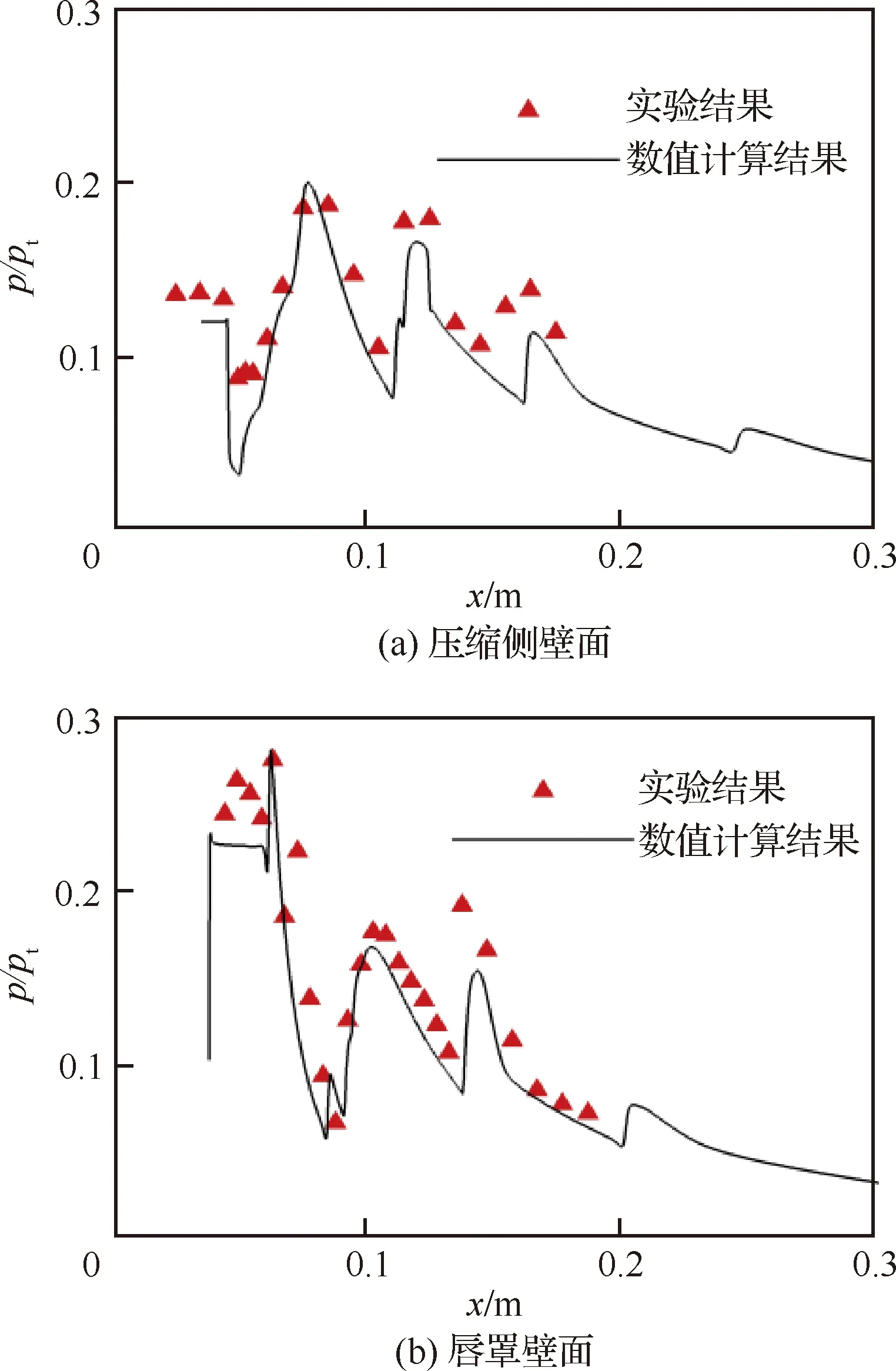
圖8 實驗和數值計算下壁面壓力分布對比Fig.8 Comparison of wall pressure distributions between current simulation and experimental data

3 分析與討論

基于數值仿真方法對進氣道流場展開計算。首先以CR=1.7的進氣道為對象，研究唇口角對進氣道設計條件下總壓恢復性能、阻力性能以及加速自起動過程中進氣道起動性能的影響。接著研究不同內收縮比下唇口角對進氣道綜合性能的影響規律。在本文計算方案中唇口角變化范圍為0°～8°。為細致捕捉最佳唇口角，在設計條件下進氣道流場計算中唇口角間隔取0.1°，加速自起動過程中唇口角最小間隔取1°。

3.1 唇口角對總壓恢復性能的影響

圖9為進氣道總壓恢復系數隨唇口角的變化規律。從圖中可以看出存在一個最佳唇口角使總壓恢復系數最大，將該唇口角記為opt, ，而當唇口角過大或過小時進氣道總壓恢復性能均下降。例如，當唇口角為0°、8°時，進氣道總壓恢復系數分別為0.732 9、0.745 4，而當唇口角取至opt, =4.3°時，總壓恢復系數達到0.764 0，分別提高了4.24%、2.50%。這表明合理設計唇口角可顯著提高進氣道總壓恢復性能。

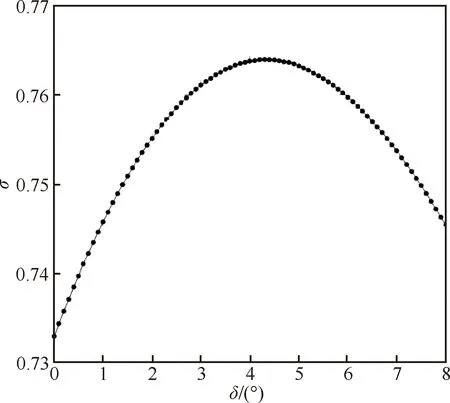
圖9 進氣道總壓恢復系數隨唇口角的變化規律Fig.9 Distribution of total pressure recovery coefficients with cowl lip angle increase

圖10給出唇口角分別為0°、4.3°、8°時流場馬赫云圖和總壓恢復系數分布。可以看出進氣道外壓縮段對氣流進行等熵壓縮，基本沒有造成流動損失。由于超聲速流動中位于下游的唇罩并不影響上游流場，因此3種唇口角下進氣道外壓縮段流場結構完全相同。當氣流進入內壓縮段時，流場表現出明顯差異。唇口角為0°時，唇罩型線與入口處氣流形成較大對沖角，由此產生一道強烈的唇口激波，唇口激波經壁面反射形成反射激波，氣流經過唇口激波及其反射激波后流動速度顯著降低，總壓恢復系數也明顯下降。唇口角為4.3°時，由于唇罩壁面與入口氣流的對沖角減小，唇口激波強度大大減弱。從總壓恢復系數分布來看，此時進氣道入口處只有輕微總壓損失。而當唇口角增加至8°，唇罩型線在起始位置處向外偏轉，氣流經過唇口時產生局部膨脹，流動速度增加。而后唇罩型線迅速向內偏轉，對氣流產生強烈壓縮作用，唇罩側壁面產生的一系列壓縮波在流道內匯聚成激波，文中稱這道激波為匯聚激波。氣流經過匯聚激波后速度明顯降低，流動損失增加。這一結果表明，對于總/內收縮比一定的進氣道，并非唇口角越大越有利于提升總壓恢復性能，而應當通過唇口角設計盡量避免內收縮段形成過強的激波結構。

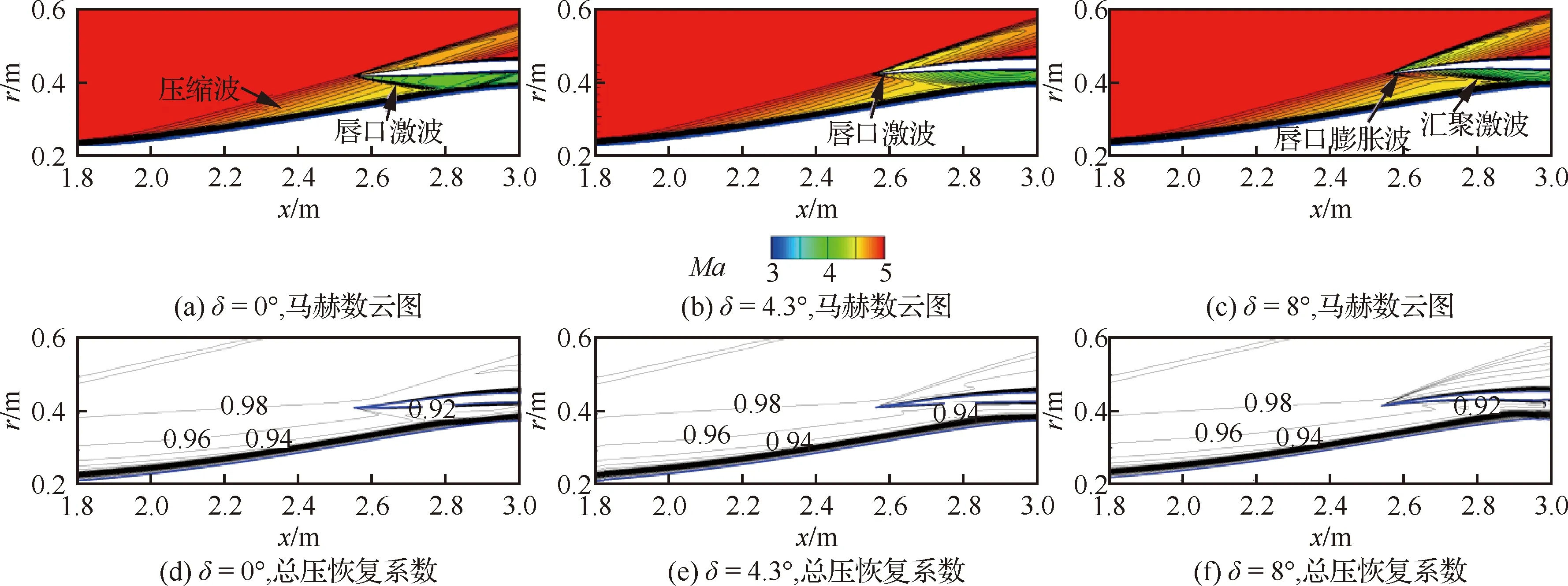
圖10 不同唇口角下進氣道流場馬赫云圖和總壓恢復系數分布Fig.10 Mach contours and total pressure recovery distributions of inlet with different cowl lip angles

圖11對比了不同唇口角下壓縮側壁面壓力分布。壓力曲線躍升起始點為唇口激波/邊界層干擾位置。當唇口角較小時，流場中形成強烈的唇口激波，唇口激波與壁面邊界層相互作用使壁面壓力迅速上升。隨著唇口角增加，激波/邊界層干擾位置后移，干擾強度減弱，壁面壓力躍升幅度減小。當唇口角增大至4.3°，壓力曲線峰值最小。隨著唇口角進一步增加，壓力峰值又開始增大。這是因為過大的唇口角使內收縮段形成匯聚激波，匯聚激波與壁面邊界層發生干擾造成壁面壓力再次大幅提升。結合流場結構和壁面壓力分布特點發現，當唇口角為4.3°時，進氣道唇口激波強度已經減弱，而匯聚激波還未完全形成，此時流場中流動損失最小，因此總壓恢復性能最佳。

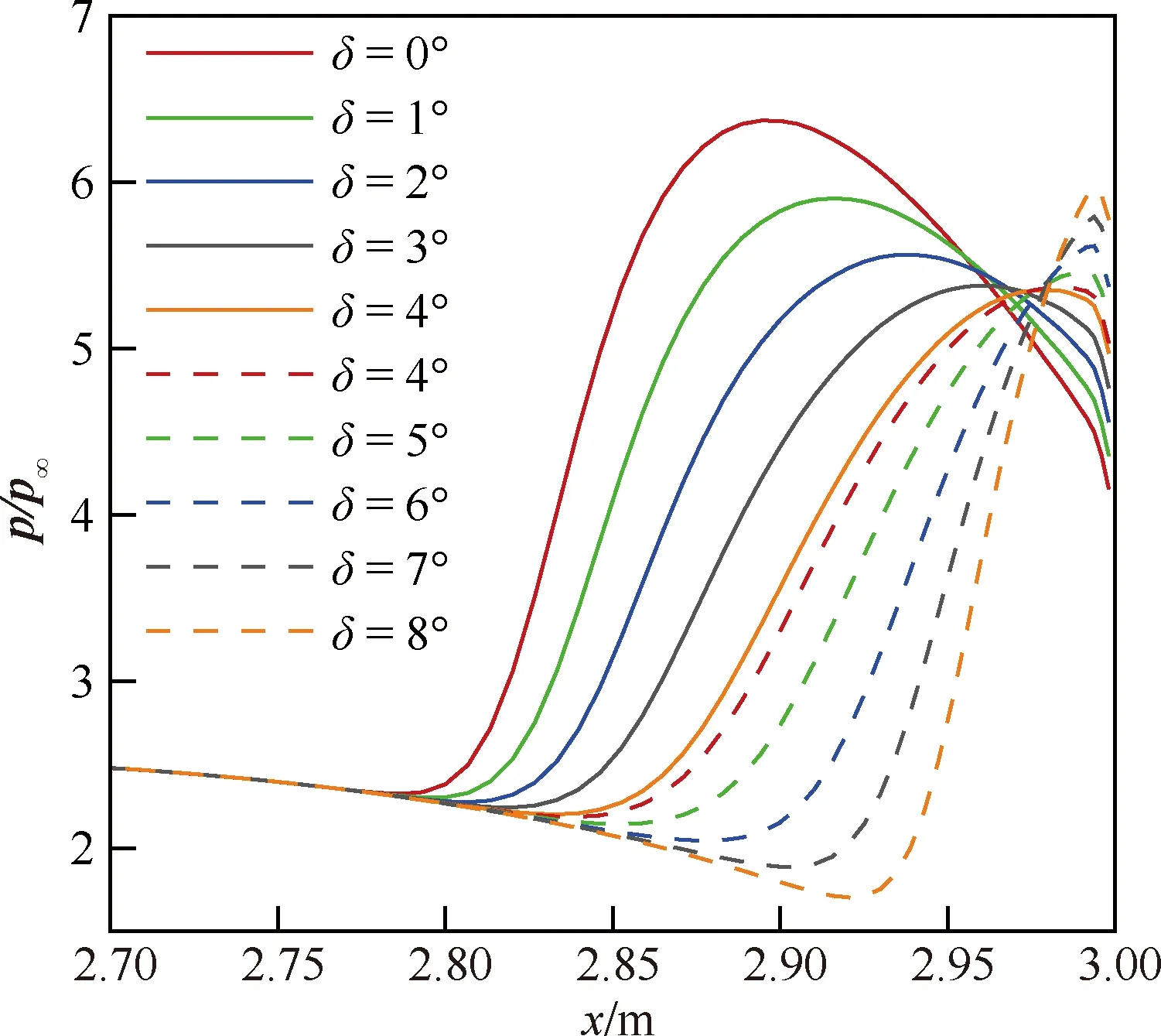
圖11 不同唇口角下壓縮側壁面壓升對比Fig.11 Wall pressure distributions of inlet with different cowl lip angles

3.2 唇口角對阻力性能的影響

圖12給出進氣道阻力系數隨唇口角的變化規律，此處進氣道阻力指由前體、進氣道壓縮壁面和內外唇罩阻力的總和。本文采用來流動壓對進氣道阻力進行無量綱化得到阻力系數(，參考面積選擇模型底面積。隨著唇口角的增大，進氣道壓差阻力系數表現出先減小后增大的趨勢，而摩阻系數幾乎不變，從而使總阻力系數表現出先減小后增大的趨勢。也就是說存在一個最佳唇口角使總阻力系數最小，記該唇口角為opt，。當唇口角取opt，=3.5°時，進氣道阻力系數為0.103 4， 而當唇口角分別取0°、8°時，阻力系數達到了0.106 7、0.109 0， 分別增大了3.09%、5.14%。這表明通過合理設計唇口角可有效減小進氣道阻力。

圖12 進氣道阻力系數隨唇口角的變化規律Fig.12 Distributions of drag coefficients with cowl lip angle increase

從阻力來源來看，模型總阻力不能只關注唇罩的影響，而應該綜合考慮唇罩內外側壁面和壓縮側壁面的影響。圖13給出了各部分阻力系數(壓差阻力與摩阻之和)隨唇口角的變化規律，其中壓縮側壁面阻力特指前體和進氣道壓縮型面阻力的總和。當唇口角較小時，唇口內激波使唇罩內側壁面壓力上升，唇罩內側阻力為負值。隨著唇口角增大，唇口激波逐漸減弱，直至變為膨脹波，此時唇罩內側阻力變為正值并不斷增大。同時，隨唇口角增大，唇口外激波不斷增強，唇罩外型面波阻顯著升高。因此，唇罩內外側阻力均隨唇口角的增大而增加。另一方面，由圖13可知，隨唇口角增大，壓縮側壁面壓力值先減小后增大。然而由于高壓區逐漸后移，壁面壓力沿水平方向的分量減小，使壓縮側壁面阻力隨唇口角增加呈減小的趨勢。最終在內外唇罩阻力和壓縮側壁面阻力的共同影響下，進氣道總阻力隨唇口角增大呈先減小后增大的變化規律。

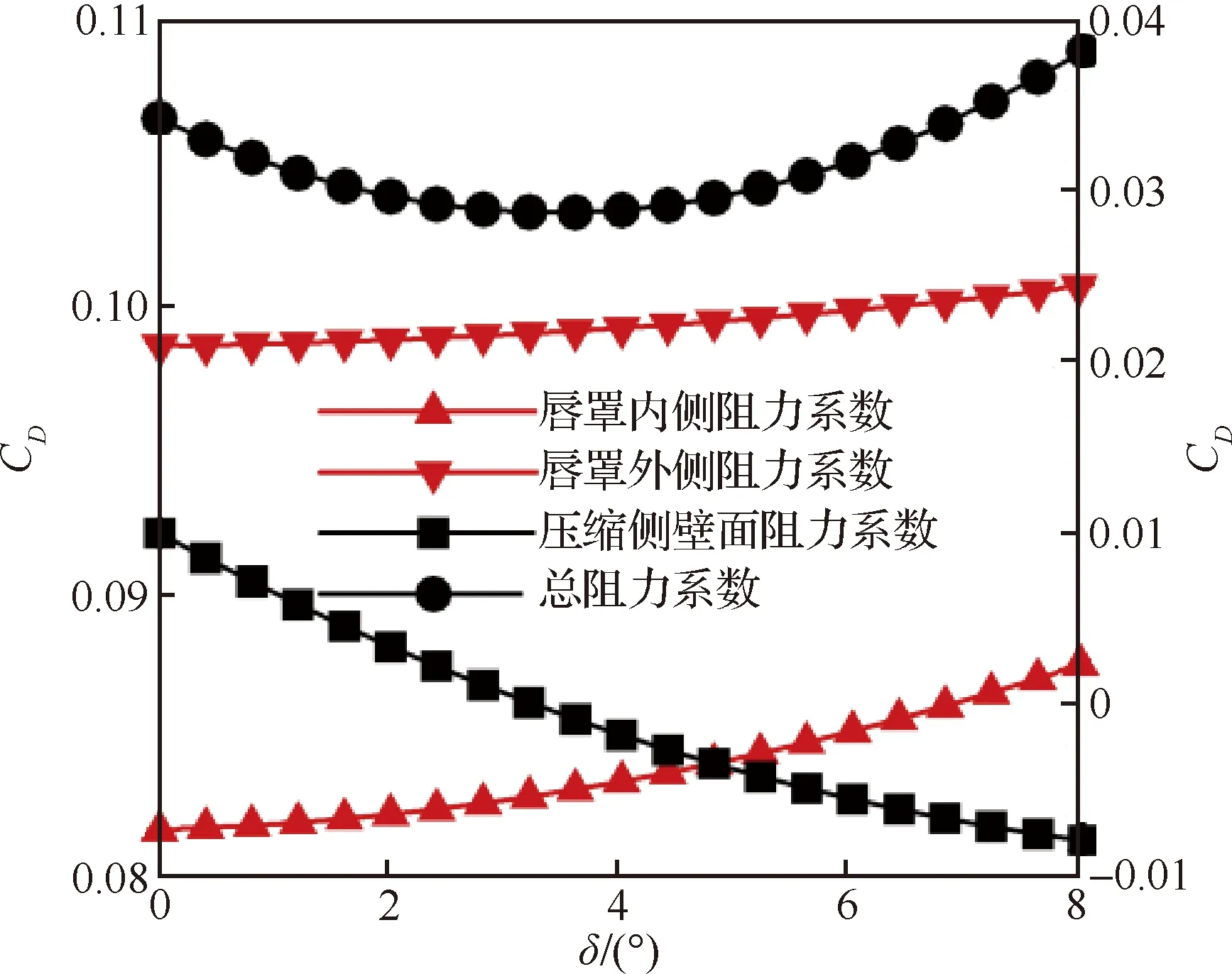
圖13 進氣道各部件總阻力系數隨唇口角的變化規律Fig.13 Distributions of total drag coefficients with cowl lip angle increase

3.3 唇口角對起動性能的影響

高超聲速進氣道加速自起動過程可描述如下：首先，由于飛行器飛行速度較低，進氣道喉部通流能力不足，發生壅塞，進氣道入口處產生大尺度分離區造成唇口溢流，使捕獲流量下降，此時進氣道處于不起動狀態。隨著來流馬赫數增大，大尺度分離區被吞入，唇口溢流消失，管道內形成通暢的超聲速流動，進氣道進入起動狀態。進氣道由不起動狀態轉變為起動狀態所對應的來流馬赫數稱為自起動馬赫數。

圖14為進氣道自起動馬赫數隨唇口角的變化規律。唇口角過大或過小時，進氣道起動性能均較差，同樣存在一個最佳唇口角度使進氣道起動性能最佳，記該唇口角為opt，。當唇口角取至opt，=3°時，來流馬赫數增加至3.25時進氣道就進入起動狀態。

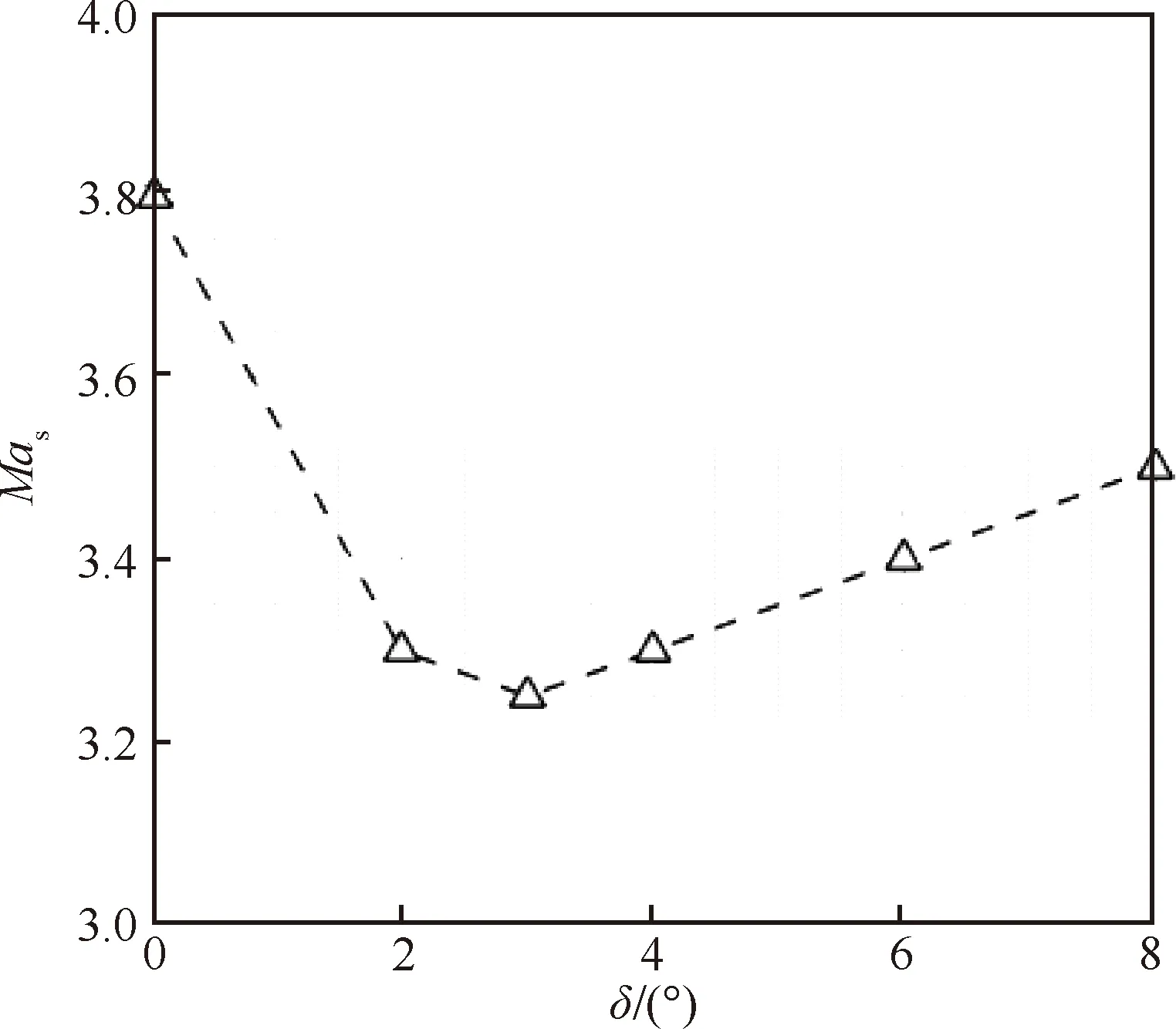
圖14 進氣道自起動馬赫數隨唇口角的變化規律Fig.14 Distribution of starting Mach number with cowl lip angle increase

為進一步研究唇口角對進氣道起動的作用機理，對進氣道起動過程開展分析。圖15為來流馬赫數為3.0時進氣道在不同唇口角下的流場亞聲速區分布及壁面壓力。當進氣道處于不起動狀態時，入口處存在大尺度分離區結構。在分離區及其波系作用下，壓縮側壁面壓力形成2次躍升，其中第1次躍升由分離區起始位置處分離激波導致，第2次躍升由分離區結束位置再附激波導致。由于分離區內壓力變化很小，因此兩次躍升之間形成了壓力平臺。在唇口激波的作用下，唇罩側壁面起始處壓力突增。接著在分離區背風面膨脹波的影響下，唇罩壁面壓力下降。隨后再附激波與唇罩側邊界層發生干擾，壁面壓力再次上升。

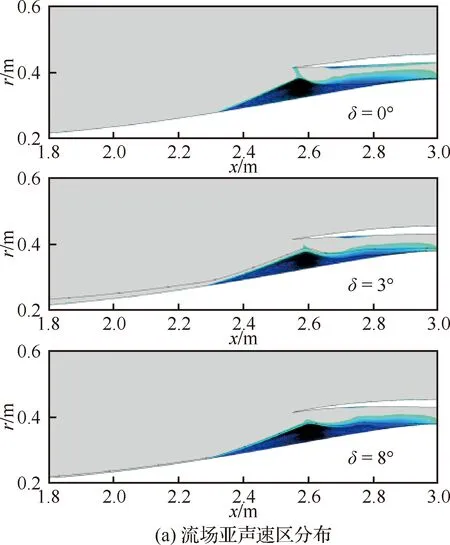
圖15 Ma=3.0下進氣道在不同唇口角下流場亞聲速區及壁面壓力分布Fig.15 Distributions of subsonic zone and wall pressure of inlets with different cowl lip angles at Ma=3.0

對于唇口角為0°的構型，唇口激波后為亞聲速區，分離激波造成的第1次壓力躍升較高，唇口處壓力達到14。說明此時進氣道流場唇口激波強烈，分離區很難被吞入。當唇口角增至3°時，進氣道入口處形成超聲速通道，由分離激波造成的壓縮側壁面壓力躍升變小，同時唇口處壓力也顯著減小。當唇口角增加至8°，唇口處壓力進一步降低，不足7。但由于內收縮段型面迅速收縮，分離區尺度增大，壓縮側壁面壓力在內收縮段有所增加，形成較大逆壓梯度。分離區強逆壓梯度作用下，具有較強的自持能力，在來流馬赫數較高時才被吞入，表現出較差的起動性能。

3.4 不同內收縮比下唇口角對進氣道性能的影響

對于二維軸對稱進氣道，內收縮段由唇罩內壁面和壓縮側壁面共同構成。唇口角通過改變唇罩型線調整進氣道沿程內收縮規律，從而影響進氣道性能。同樣地，壓縮側型線對進氣道性能也有重要影響，并且壓縮側型線不同，唇口角對進氣道性能的影響規律也有所差別。3.3節研究了內收縮比為1.7的進氣道唇口角對總壓恢復性能、阻力性能和起動性能的影響。為不失一般性，本節研究內收縮比介于1.5～1.9時的進氣道唇口角對總壓恢復性能、阻力性能和起動性能的影響。

采用參數化方法對壓縮壁面展開設計，設計中保證點處光滑及點處水平，通過改變曲線形狀獲得不同內收縮比的進氣道構型。圖16給出內收縮比CR分別為1.5、1.6、1.7、1.8、1.9的進氣道壓縮側壁面示意圖。圖中進氣道壓縮型線具體設計方法及設計參數可參考文獻[22]。如圖所示壓縮側壁面曲線由上至下，進氣道內收縮比依次增大。

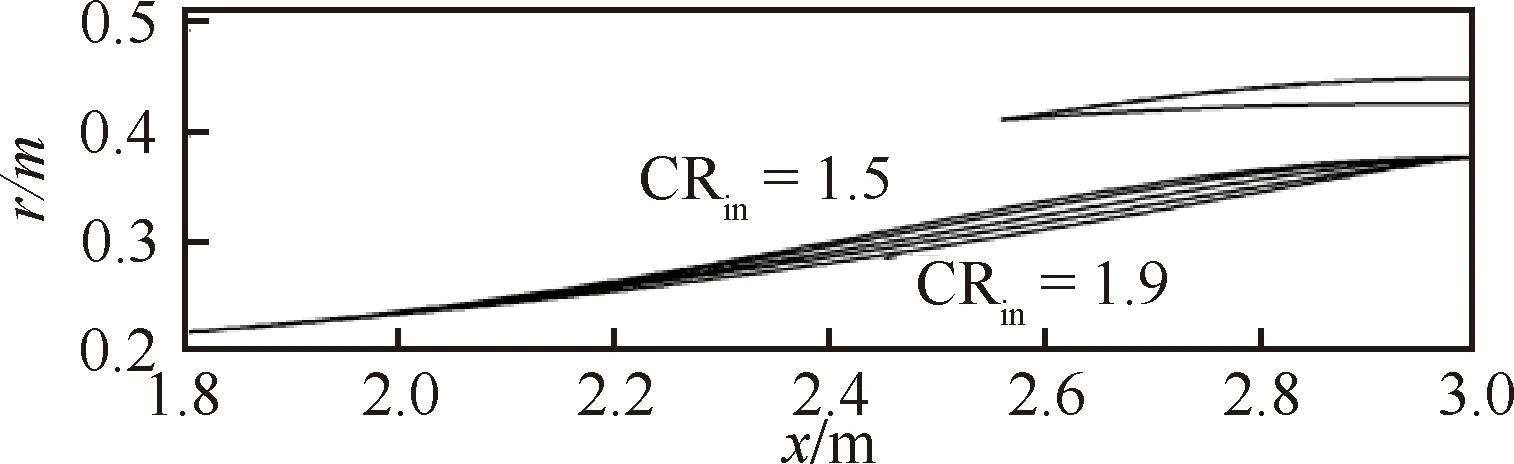
圖16 不同內收縮比的進氣道壓縮側型線對比Fig.16 Comparison of inlet configurations with different internal contraction ratios

3.4.1 對總壓恢復性能的影響規律

圖17給出不同內收縮比下唇口角對進氣道總壓恢復系數的影響規律。圖中每一個點表示在特定內收縮比和唇口角下進氣道總壓恢復系數，其中位于同一條曲線上的進氣道具有相同的內收縮比，其數值標注在曲線上。可以看出，隨內收縮比增大，進氣道總壓恢復性能整體上升。此外，進氣道內收縮比不同，對應的opt，也不同，具體來說存在內收縮比越大，opt，越小的變化規律。例如，CR=1.5的進氣道對應的opt，為6.2°，而對于CR=1.9的進氣道，當唇口角取至3.3°時總壓恢復系數達到最大值。分析表明，內收縮比較小的進氣道外壓縮段對氣流的壓縮作用強，氣流在進氣道入口處流動角較大，因此需要設計更大的唇口角以避免產生強烈的唇口激波。相反，進氣道內收縮比較大時，氣流在外壓縮段的壓縮程度弱，入口處氣流流動角小，采用較小的唇口角就能減弱唇口激波強度。同時較小的唇口角也避免了因流道過快收縮而形成的匯聚激波。因此唇口角設計時需考慮進氣道入口處氣流流動情況，使唇口激波強度盡可能低，同時避免內收縮段形成匯聚激波。

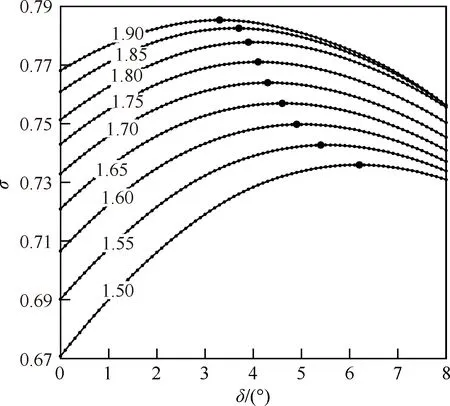
圖17 不同內收縮比的進氣道總壓恢復系數隨唇口角的變化規律Fig.17 Distribution of total pressure recovery coefficients with increase of cowl lip angle of inlets with various internal compression ratios

進一步地，對不同內收縮比的進氣道入口處氣流流動方向與opt，的關系展開研究。由于外壓縮段采用曲面壓縮，進氣道入口處流動不均勻，無法直接獲得氣流當地流動角。以進氣道入口物面角(見圖3)反映入口處氣流流動方向。圖18分別給出不同內收縮比下進氣道入口處物面角、使總壓恢復性能最佳的唇口角及二者的差值。進氣道入口處物面角和最佳唇口角均隨內收縮比的增大而逐漸減小，但二者之差始終在5°附近，也就是說當唇口角設計為入口處物面角減5°左右，進氣道可達到最佳總壓恢復性能。

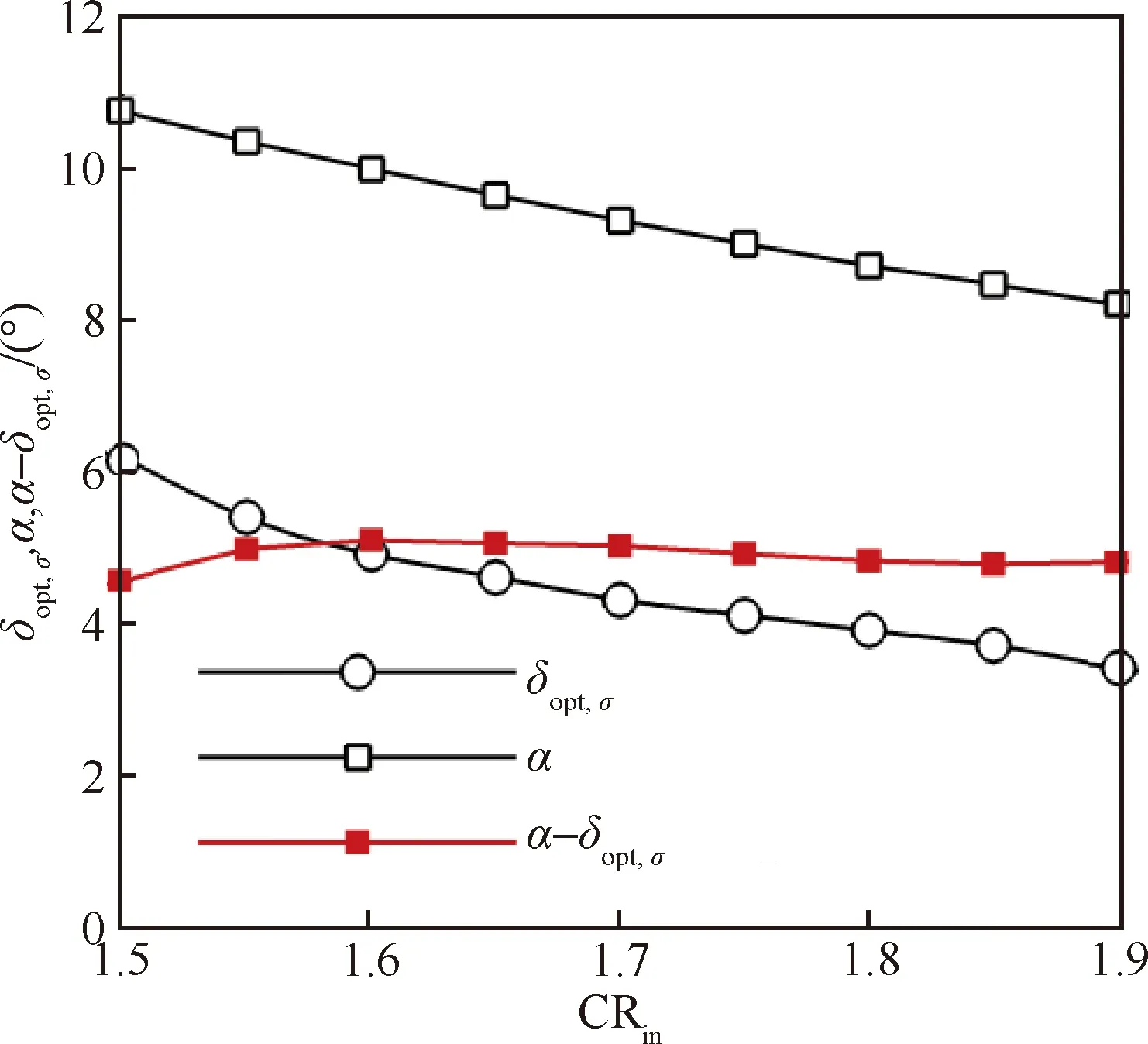
圖18 進氣道入口處物面角與使總壓恢復性能最佳的唇口角對比Fig.18 Comparison of wall angle at inlet entrance and optimal cowl lip angle in view of total pressure recovery

3.4.2 對阻力性能的影響規律

圖19給出不同內收縮比下進氣道阻力系數隨唇口角的變化。內收縮比由1.50增大至1.85過程中，進氣道阻力出現整體下降，而內收縮比為1.90的進氣道阻力稍有增大。最終使進氣道阻力系數最小的內收縮比為1.85，對應的唇口角為3.6°。此外，所有內收縮比下阻力系數均隨唇口角增大表現出先減小后增大的規律，但使進氣道阻力系數最小的最佳唇口角并不相同。具體來說，內收縮比在1.50～1.65范圍內，opt，隨內收縮比的增大不斷減小，內收縮比由1.65增至1.90 的過程中opt，在3.3°～3.8°范圍內小幅變化，未表現出明顯規律。分析發現，內收縮比較小時入口處氣流流動角較大，設計較大的唇口角才能避免強烈唇口激波。此時雖然唇口角的增大會增加唇罩阻力，但由于唇口激波減弱，壓縮側壁面阻力顯著降低，使得此時進氣道總阻力最小。而內收縮比較大時，氣流壓縮主要集中在內收縮段后半部分，此處壓縮側型面已基本轉為水平，對進氣道阻力的影響有限。為降低進氣道阻力，唇口角設計中只需要避免產生過強的唇口內外激波，所以此時opt，變化幅度很小。

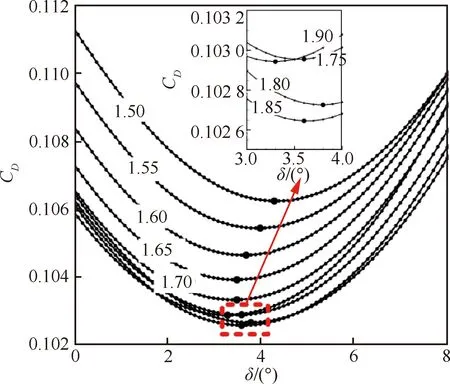
圖19 不同內收縮比的進氣道阻力系數隨 唇口角的變化規律Fig.19 Distribution of drag coefficients with increase of cowl lip angle of inlets with various internal compression ratios

3.4.3 對起動性能的影響規律

對小內收縮比(CR=1.5)、大內收縮比(CR=1.9)進氣道的加速自起動過程進行計算，分析不同內收縮比水平下唇口角對起動性能的影響規律。

圖20給出不同內收縮比下起動馬赫數隨唇口角的變化。對于CR=1.5的進氣道構型，唇口角取0°時，進氣道直到來流馬赫數增大至4.1時才進入起動狀態。分析發現唇口角過小時，會產生強烈唇口激波，分離區在起動過程中位置幾乎不變，很難被吞入進氣道內，造成起動性能嚴重下降。隨著唇口角增大，唇口激波強度減弱，進氣道起動性能迅速改善。當唇口角增至5°，進氣道在來流馬赫數增大至3.05時就進入起動狀態。隨著唇口角進一步增大，起動馬赫數稍有上升，但增幅不大。對于CR=1.9的進氣道，當唇口角為1°時，進氣道自起動馬赫數最低(=3.52)。隨著唇口角增大，進氣道起動性能迅速惡化，唇口角為8°時進氣道在來流馬赫數增至4.6時才進入起動狀態。分析起動過程發現，唇口角過大時唇口激波變弱，分離區可輕易進入內收縮段。但由于內收縮段型面迅速收縮，分離區在內收縮段形成穩定的駐留，由于缺乏唇口溢流的調節作用，進氣道起動性能惡化。

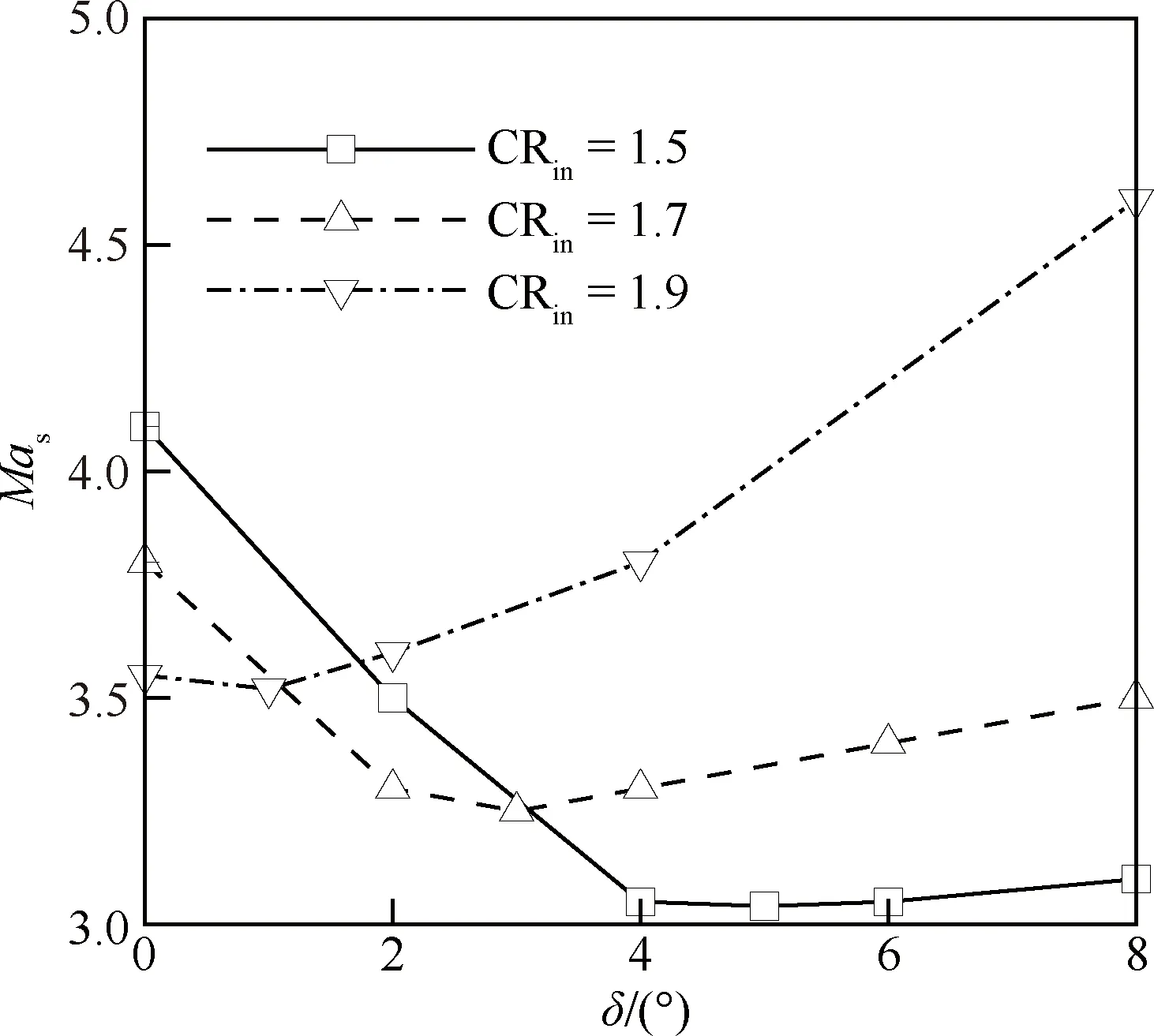
圖20 不同內收縮比的進氣道自起動馬赫數 隨唇口角的變化規律Fig.20 Distribution of starting Mach numbers with increase of cowl lip angle of inlets with various internal compression ratios

3.5 多目標考慮下進氣道唇口角設計

通過3.4節的研究，分別獲得使總壓恢復性能、阻力性能和起動性能最佳的唇口角。然而在實際進氣道設計中需綜合考慮以上性能，因此如何在唇口角設計中兼顧進氣道多種性能指標是設計者需要面對的問題。

首先分析不同內收縮比下opt，和opt，的關系。圖21給出了各內收縮比和唇口角下進氣道總壓恢復系數和阻力系數分布。圖中每條曲線上的進氣道構型具有相同的內收縮比，9條曲線由下至上，內收縮比依次增大，沿曲線由下端點至上端點唇口角依次由0°增至8°。對于每個點表示的進氣道，點的位置越靠左，表明阻力系數越小；點的位置越靠上，表示總壓恢復系數越高。由于唇口角對總壓恢復系數和阻力系數的影響規律并不完全一致，對于該二目標問題，存在Pareto前緣(見圖21中藍色區域)。位于Pareto前緣上的解意味著當兩目標被認為同等重要時解空間中沒有比它們更好的解。為兼顧進氣道總壓恢復性能和阻力性能，唇口角的選擇應位于Pareto前緣上。隨著內收縮比增大，Pareto前緣逐漸變窄，這意味著通過唇口角設計更容易同時提高總壓恢復性能和阻力性能。內收縮比為1.85、1.90的進氣道Pareto前緣變為一點，此時唇口角取該值時進氣道可同時獲得最佳總壓恢復性能和阻力性能。值得注意的是內收縮比為1.85的進氣道唇口角取至最佳值時，在所有進氣道構型中具有最小的阻力系數；內收縮比為1.90的進氣道唇口角取至最佳值時具有最大的總壓恢復系數。也就是說進氣道內收縮比為1.85、1.90時，不僅可通過唇口角設計獲得各自內收縮比下最佳總壓恢復性能和阻力性能，而且可分別實現所有內收縮比下最小阻力系數和最高總壓恢復系數。

圖21 不同內收縮比和唇口角下進氣道總壓恢復系數和阻力系數分布Fig.21 Total pressure recovery coefficients and drag coefficients of inlets with various internal contraction ratios and cowl lip angles

其次分析opt，和的相對關系。隨著內收縮比增大，二者均表現出下降的趨勢。其原因是在進氣道總壓恢復性能和起動性能中，唇口激波都發揮了重要作用。當內收縮比較小時，若唇口角取值偏小，進氣道總壓恢復性能因強烈唇口激波而下降。同時，強烈唇口激波在進氣道起動過程中使大尺度分離區不易被吞入，造成起動性能惡化。而對于內收縮比較大的進氣道，若唇口角偏大，進氣道設計條件下內收縮段因型面過度收縮產生匯聚激波，造成總壓恢復性能下降。同時過大的唇口角在起動過程中會使大尺度分離區進入內收縮段并形成穩定駐留，造成起動性能惡化。因此在進氣道唇口角設計中，為提高總壓恢復性能和起動性能，應充分考慮入口處氣流流動情況，通過唇口角設計合理組織進氣道波系結構，避免形成強烈唇口激波，同時內收縮段型面應避免劇烈收縮。

圖22給出opt，、opt，和隨內收縮比的變化規律。在研究的內收縮范圍內三者并不重合，這表明無法通過唇口角設計同時獲得最佳總壓恢復性能、阻力性能和起動性能。但可以看出三者均隨內收縮比的增大整體表現出下降趨勢，數值相差并不大。另外，從圖17、圖19可知，總壓恢復系數和阻力系數均隨唇口角大致呈二次曲線分布，也就是說當唇口角取至最佳唇口角附近時，進氣道總壓恢復性能和阻力特性對唇口角的變化并不敏感。由圖20可知，當唇口角在最佳唇口角附近時，進氣道自起動馬赫數變化幅度很小，表明在一定唇口角范圍內，進氣道均具有較好的起動性能。這些特點為通過唇口角設計提高進氣道綜合性能提供可能。例如對于CR=1.5進氣道，當唇口角取至5.0°時，進氣道起動性能最佳，而此時總壓恢復系數比最佳唇口角時只下降了0.30%， 阻力系數比最佳唇口角下只增加了0.12%。 對于CR=1.7的進氣道，當唇口角取至阻力系數最小的3.5°時，總壓恢復系數僅下降0.14%， 進氣道在來流馬赫數增大至3.3時即可實現起動。而對于CR=1.9的進氣道，唇口角為3.3° 時，總壓恢復性能和阻力性能為最佳狀態，進氣道在來流馬赫數為3.7左右實現起動。可以認為當唇口角取值位于由圖22中3條最佳唇口角曲線構成的輪廓范圍內時，進氣道可獲得良好的總壓恢復性能，阻力性能和起動性能。

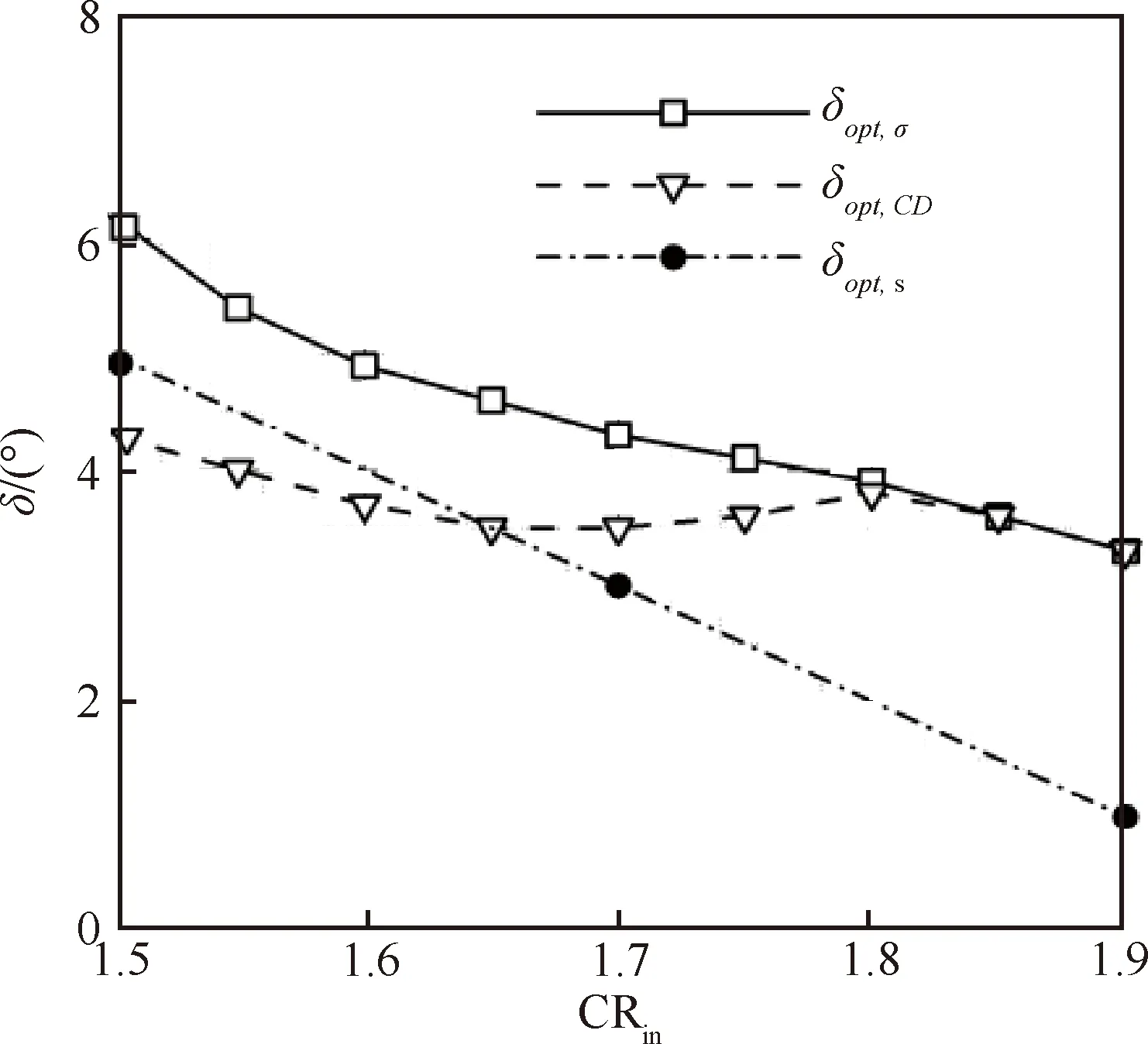
圖22 δopt，σ、δopt，CD和δopt，s隨內收縮比的變化規律Fig.22 Distributions of δopt，σ, δopt，CD and δopt，s with increase of internal contraction ratio

4 結 論

以具有長前體的高超聲速進氣道為研究對象，對進氣道唇口角展開參數化設計和分析，主要得到以下結論：

1) 對于同一內收縮比的進氣道，唇口角過大或過小時總壓恢復性能均下降，存在1個最佳唇口角使總壓恢復系數最大。

2) 隨唇口角增加，內外側唇罩產生的阻力均增大，而壓縮側壁面阻力逐漸減小，在三者共同作用下存在1個最佳唇口角使進氣道阻力最小。

3) 唇口角對起動性能有重要影響，唇口角過大或過小均不利于進氣道起動，存在1個最佳唇口角使起動性能最佳。

4) 隨內收縮比的增大，使總壓恢復性能、阻力性能和起動性能最佳的唇口角整體表現出下降趨勢。唇口角設計中需考慮進氣道入口處氣流流動情況，使唇口激波強度盡可能低，同時避免內收縮段型面過度收縮。

5) 使總壓恢復性能、阻力性能和起動性能分別最佳的唇口角并不重合，但總體而言三者相差不大，一定程度上可以認為通過唇口角設計可使進氣道同時達到較好的總壓恢復性能、阻力特性和起動性能。