風洞虛擬飛行試驗模型繩系并聯支撐機構

吳惠松，林麒，柳汀, 劉震, 師璐，王曉光

廈門大學 航空航天學院，廈門 361102

風洞虛擬飛行試驗(Wind Tunnel Based Virtual Flight Testing, WTBVFT)是近年發展起來的一種連接傳統風洞試驗和飛行試驗之間紐帶的風洞試驗技術，它采用某種支撐裝置將飛行器模型支撐在風洞試驗段中進行吹風試驗，約束模型的3個線位移，釋放模型的3個轉動角位移，按照模擬相似準則設計飛行控制律，操縱舵面來控制模型偏轉，檢驗其操縱響應特性，研究氣動/運動耦合機理，達到建立氣動/運動/控制一體化評估試驗平臺的目的。同時，支撐裝置還必須滿足轉角范圍大、支撐干擾小等要求，以及具備3個轉動自由度的自由耦合和解耦運動功能。

為此，眾多學者對風洞虛擬飛行試驗技術開展研究。美國Gebet、Wehef、Lawrence等采用多根鋼繩通過模型外部軸承環將導彈模型懸掛支撐在風洞中開展虛擬飛行試驗，實現了導彈的俯仰、滾轉和偏航運動。英國Lowenberg和Kyle設計了鐘擺式支撐裝置，用于研究飛行器的俯仰單自由度及俯仰和升沉兩個自由度的被動驅動運動；Davison、Gatto等設計了硬式三自由度支撐機構，并進行系統建模和穩定性導數試驗；Pattinson等研發了五自由度支撐機構，對機構進行動力學建模，開展俯仰極限振蕩研究等試驗。俄羅斯中央空氣流體動力研究院研發了三自由度背撐式虛擬飛行試驗支撐機構，開展了大迎角失速/偏離、飛行控制律算法驗證等研究。國內趙忠良等在2.4 m跨聲速風洞中采用吊架式模型支撐系統，實現模型俯仰、滾轉自由運動及偏航驅動控制運動，開展氣動/運動耦合機理研究；李浩開展了風洞虛擬飛行相似準則和模擬方法研究；郭林亮等采用三自由度接觸型球鉸支撐機構、兩自由度萬向鉸和旋轉曲桿組合三自由度支撐機構開展動力學特性研究；岑飛等開展了模型自由飛試驗和虛擬飛行試驗相關技術研究；南京航空航天大學、中航工業空氣動力研究院、中國航天空氣動力技術研究院等單位也開展了相關研究。

本文充分利用繩系機器人用于風洞試驗的模型支撐機構簡單，且繩索鉸接點具備球副的功能，以及繩索對氣流干擾小、可智能控制等優勢，基于螺旋理論的機構構型設計方法和自由度計算原理，設計了風洞虛擬飛行試驗模型繩系支撐機構(Wire Driven Parallel Robot suspension for Virtual Flight Testing model,WDPR-VFT)，進行穩定性分析和結構優化設計；再對其機構進行運動學和動力學建模，并進行相應的仿真分析和試驗驗證。

1 構型設計與分析

1.1 構型設計

本文在空間平行四桿機構和平面三平行五桿機構的基礎上，結合風洞虛擬飛行試驗模型支撐的需求，設計了兩個空間五桿平行四邊形機構經正交疊加組合，并分別與上下兩個偏航轉動副構成虛擬飛行試驗模型支撐機構，如圖1(a)所示。圖1(b)給出的支撐平臺可實現釋放或鎖定模型的轉動自由度，及調整模型不同的轉動幅度的功能。即該機構可在風洞里支撐著飛機模型的同時通過打舵實現飛機模型做俯仰、偏航和滾轉運動，也就是做虛擬飛行試驗。

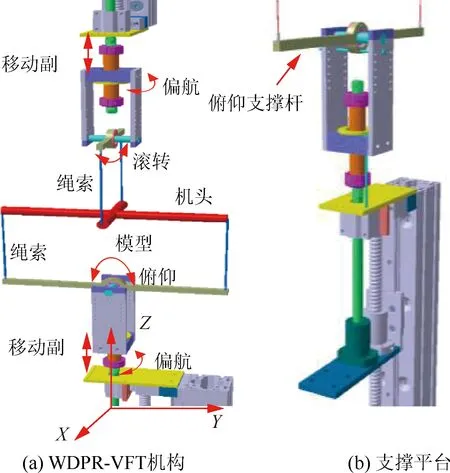
圖1 虛擬飛行試驗模型支撐機構Fig.1 Suspension mechanism of virtual flight test model

為便于計算自由度數目，先將圖1中繩索視為連桿進行分析，且用于張緊繩索的移動副不參與自由度計算。該機構可看成由上下2個串并聯分支(RR[RRPP])組成的并聯機構，每個分支中的空間五桿平行四邊形機構又可看成由與Delta機構子鏈類似的4S機構和四邊形平面垂直的轉動副構成的串并聯分支(R[RRPP])，其中R、P、S分別表示轉動副、移動副和球副，如圖2(a)所示，紅色十字架為飛機的抽象模型(即動平臺)。機構的等效結構簡圖如圖2(b)所示，不失一般性，建立圖中所示的坐標系，以便于自由度分析。

(1)

式中：4個運動螺旋分別表示單獨的平行四邊形機構的桿可繞、兩個軸線轉動，及沿、兩軸線方向的移動。其與Delta機構4S閉環子鏈類似，可將該四桿機構等效為2轉動2平移的[RRPP]機構。

表1 兩個平行四邊形機構分析Table 1 Analysis of two parallelogram mechanisms

式(1)與點的運動螺旋、偏航轉動螺旋串聯組成虛擬飛行試驗模型支撐機構第1分支(俯仰和偏航)的運動螺旋系：

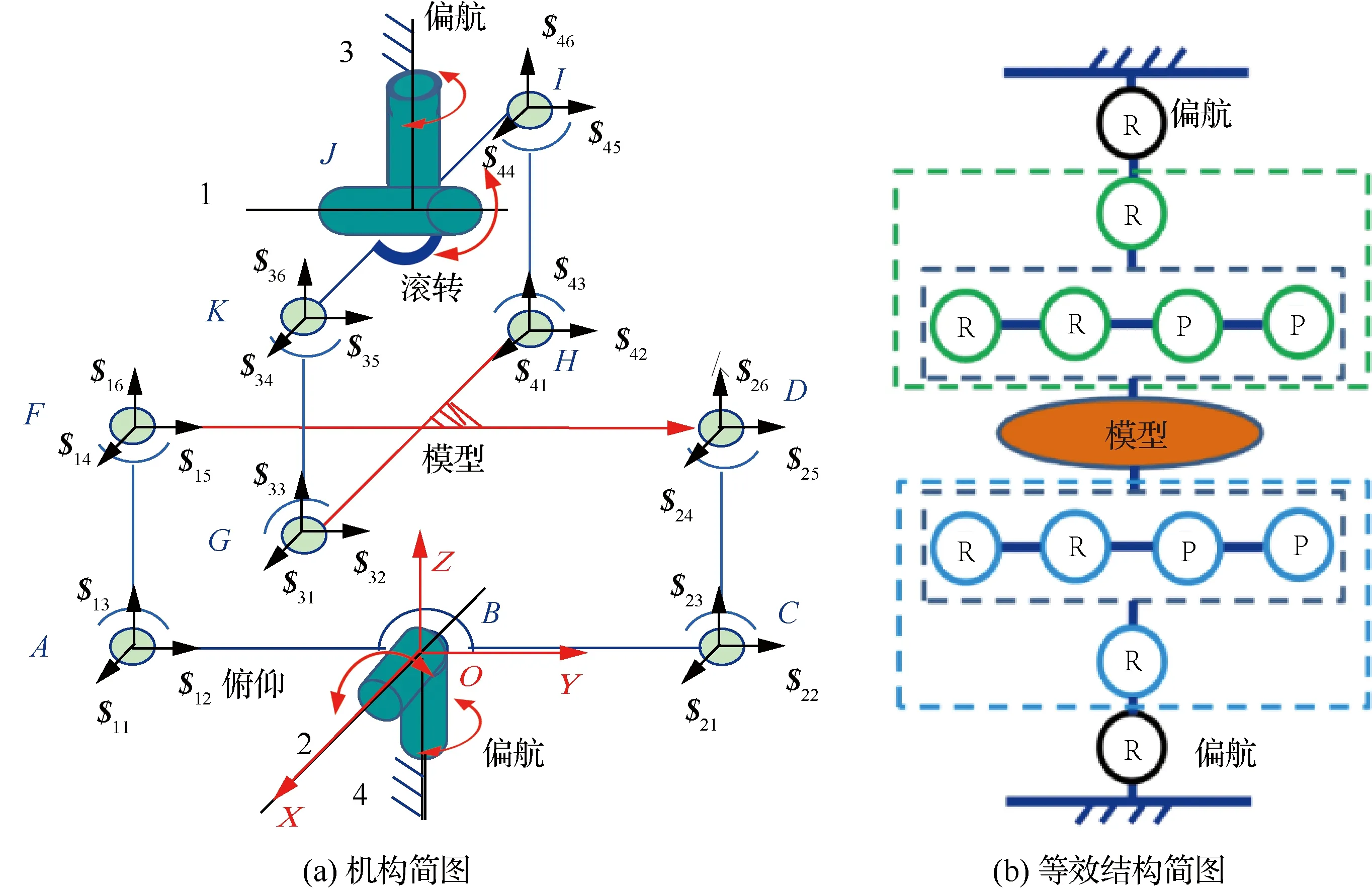
圖2 WDPR-VFT機構簡化分析Fig.2 Simplified analysis of WDPR-VFT mechanism

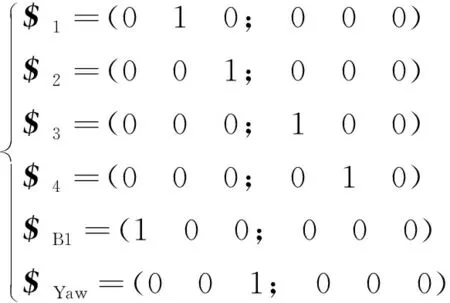
(2)

運動螺旋和均線性相關，說明第1分支存在局部自由度。

對式(2)求約束反螺旋，得

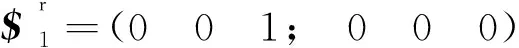
(3)

式(3)表明第1個分支對十字架模型產生了一個約束力，約束其沿軸線方向的平移。

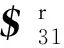
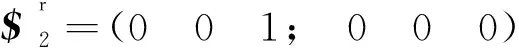
(4)

式(4)表明第2個分支對十字架模型也產生了一個約束力，約束其沿軸線方向的平移。

式(3)和式(4)共同構成虛擬飛行試驗模型支撐機構的反螺旋系，它們共同約束了十字架模型沿軸線方向的平移，即十字架模型此時有5個自由度。可以看出，兩個反螺旋線性相關，存在一個過約束。

顯然，若對于剛性硬式桿件構成的支撐，十字架模型無法繞、軸線方向旋轉，也無法沿、、方向移動。十字架模型只剩下繞軸線方向旋轉，以及繞模型質心所在相應平行四邊形機構平面上的轉動中心轉動的3個自由度。

1.2 自由度數目驗算

為驗證上述機構的自由度數目，用修正的G-K自由度公式進行計算。

十字架模型的自由度為

6(10-12-1)+28+1-(4+2+2)=3

(5)

式中：、、、和分別表示包含機架的構件數、運動副數、第個運動副的自由度數、過約束數和局部自由度數。

這里有8個局部自由度，除、、、桿分別存在一個局部自由度外，還有偏航轉動副運動螺旋分別與對應的分支組合后產生的局部自由度，以及十字架模型繞自身桿件軸線的旋轉相當于另一個平行四邊形機構的轉動，其存在2個局部自由度。

因此，若采用硬式桿件，該虛擬飛行試驗模型支撐機構自由度總數為3，即十字架模型具有俯仰、滾轉、偏航自由度，說明該機構滿足虛擬飛行試驗模型的支撐需求。

2 結構優化設計與穩定性

2.1 結構優化設計

由于真實飛機模型的氣動外形較為復雜，若采用繩索直接連接在機身外殼上，則圖1中的支撐桿、繩索和模型結合起來很難構成完整的平行四邊形機構。這會導致模型在轉動過程中，轉動前后模型質心與機構轉動中心不重合，產生不穩定現象。

為解決這個問題，在飛機模型內部設計了如圖3所示的連接機構，主要是在縱橫軸兩端分別安裝了不同長度的軸承套搖桿用于繩索連接。

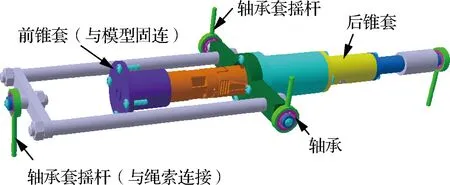
圖3 飛機模型內部連接機構Fig.3 Internal connecting mechanism of model

同時將繞軸承中心轉動的支撐桿優化設計為圖4所示的形式，即支撐桿可沿偏航轉臺方向移動，移動距離等于模型質心到原轉動中心的垂直距離。

圖4 優化后的支撐平臺Fig.4 Optimized support platform

本文采用如圖5所示的一款動態試驗標模。考慮到風洞大小以及阻塞比要求，在國內動態標準模型的基礎上進行了0.591倍縮尺比設計加工。模型幾何尺寸見圖5，總質量2.476 kg。在滿足幾何相似外，動力學相似準則主要是雷諾數。由于本文的試驗來流速度約10 m/s，特征長度取為風洞出口截面邊長450 mm，則約為3.23×10。

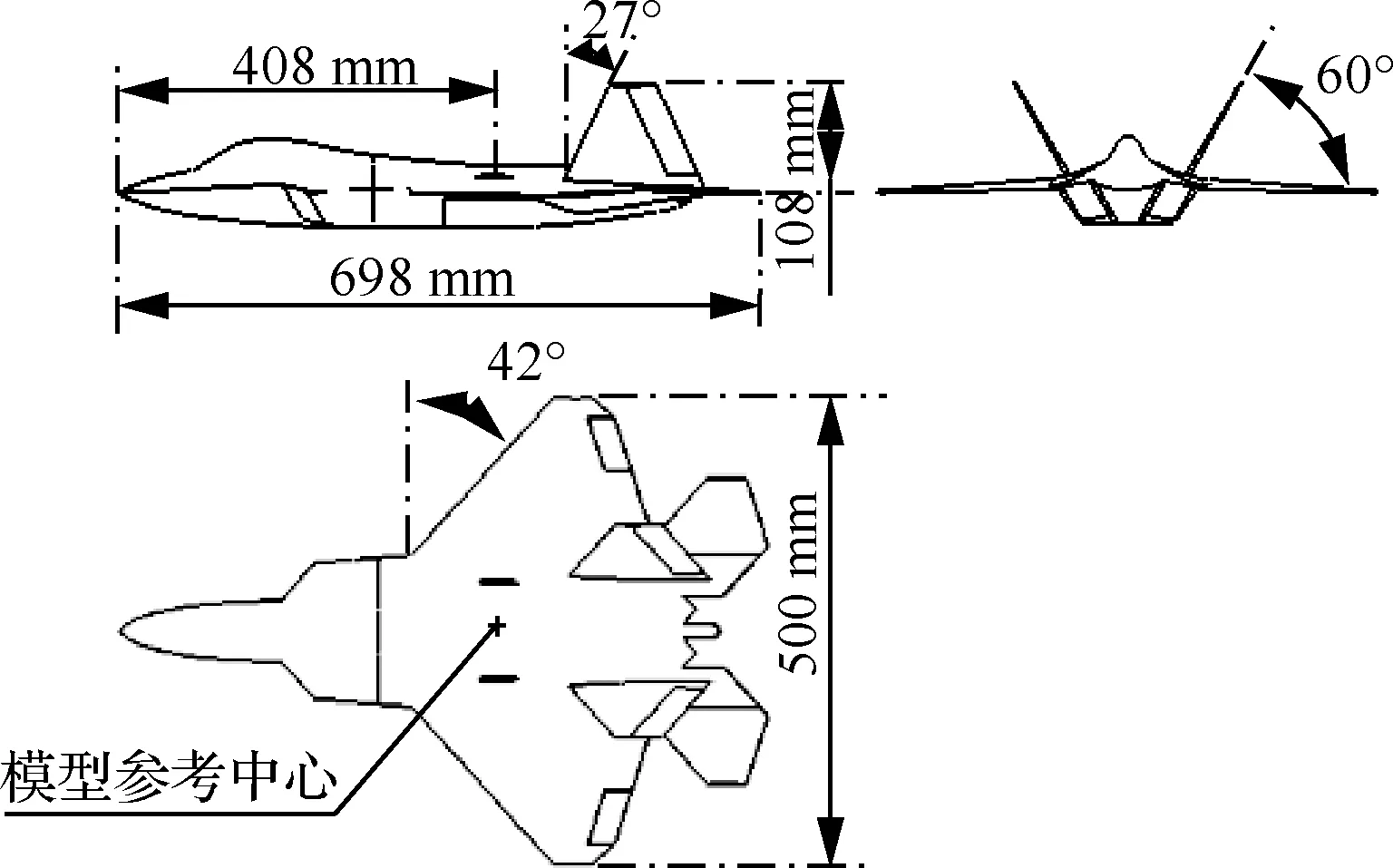
圖5 動態試驗標模縮比模型Fig.5 Scaled model of dynamic test standard model

用該動態模型以圖4的支撐平臺搭建了WDPR-VFT模型原理樣機。其機構示意圖如圖6所示。圖中所示的3個坐標系，分別是地面靜坐標系、機體坐標系(機身軸線沿方向，豎直向下指向地心)、桿件坐標系、(下標u代表上支撐桿，d代表下支撐桿)。

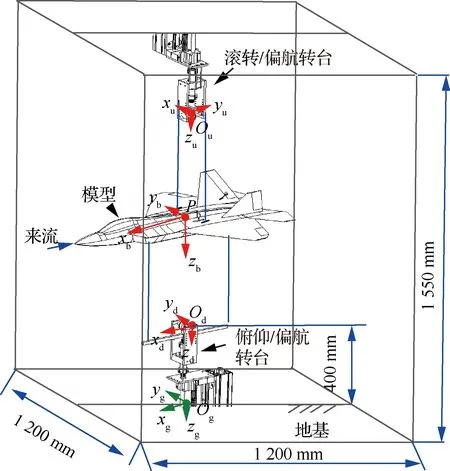
圖6 WDPR-VFT模型原理樣機示意圖Fig.6 Principle prototype of WDPR-VFT

2.2 穩定性

為驗證上述設計的WDPR-VFT機構的穩定性，采用Adams軟件進行運動仿真分析，以考察模型穩定性。假設圖5的動態標模受到舵偏作用，即相對于其抽象模型十字架的質心作用一個100 N·m 的俯仰力矩，兩根上拉和兩根下拉繩索初始預緊力分別為32.13 N和20 N。下面取其中一個平行四邊形機構(以俯仰為例)進行分析。為分析方便，將標模對稱面簡化為直線和矩形，并利用CAD作圖分析標模轉動前后質心和轉動中心是否重合。

當模型縱向豎直對稱面簡化為直線時，即繩索連接在縱橫軸上，支撐桿、兩根繩索和模型一同構成平行四邊形機構，如圖7(a)所示。當模型在俯仰力矩(例如，給模型升降舵一個舵偏角)作用下繞軸承中心轉過角時，平行四邊形機構轉動前后的模型質心、支撐機構的轉動中心均重合，不會出現振蕩現象，由于無摩擦耗散，俯仰角呈線性遞增趨勢，如圖7(b)所示。

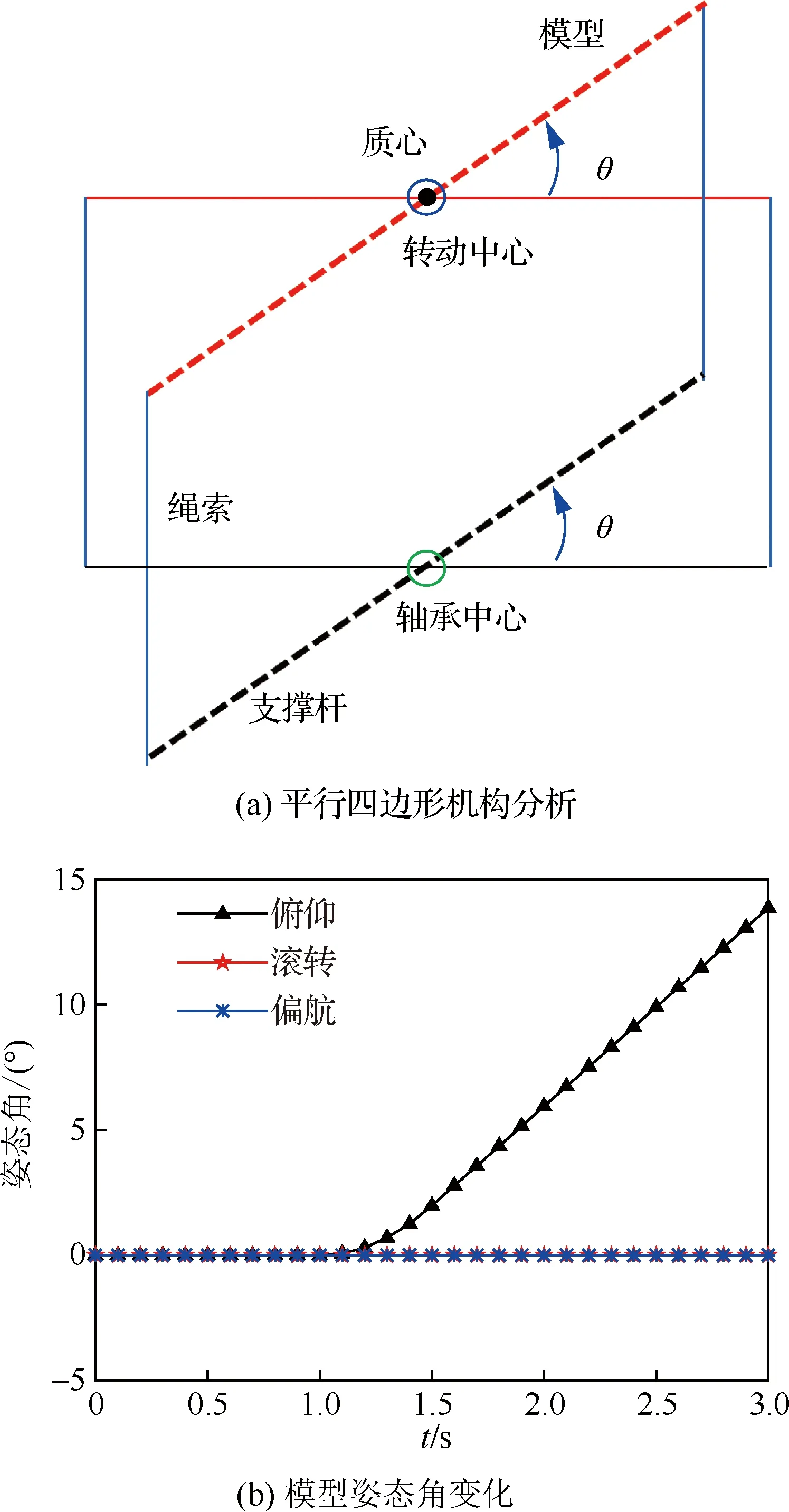
圖7 模型對稱面簡化為直線Fig.7 Model symmetry plane simplified as straight line

當模型對稱面簡化為矩形時，即繩索連接在軸承套搖桿上，支撐桿、兩根繩索、模型和兩個軸承套搖桿不能構成完整的平行四邊形機構，如圖8(a) 所示。這時若模型在俯仰力矩作用下繞軸承中心轉過角，平行四邊形機構轉動前后的模型質心、支撐機構的轉動中心會不重合，轉動過程中右邊的繩索傾斜，存在使模型恢復到平衡狀態的反力矩，俯仰角出現來回振蕩現象，如圖8(b)所示。

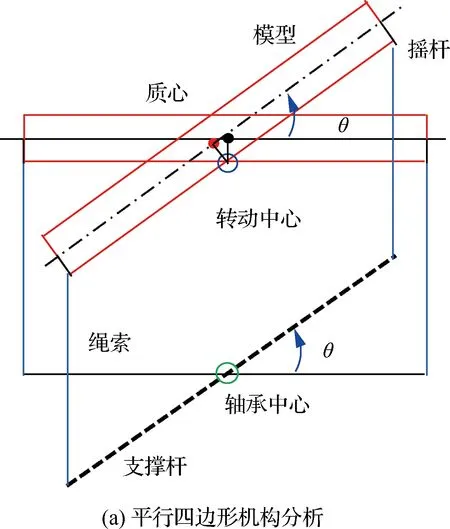
采用2.1節的結構優化，即將繞軸承中心轉動的支撐桿沿偏航轉臺方向移動，移動距離等于模型質心到原轉動中心的垂直距離，繩索長度相應加長，如圖9(a)所示。這時機構能保持穩定狀態，模型姿態角變化如圖9(b)所示，不會出現來回振蕩現象。

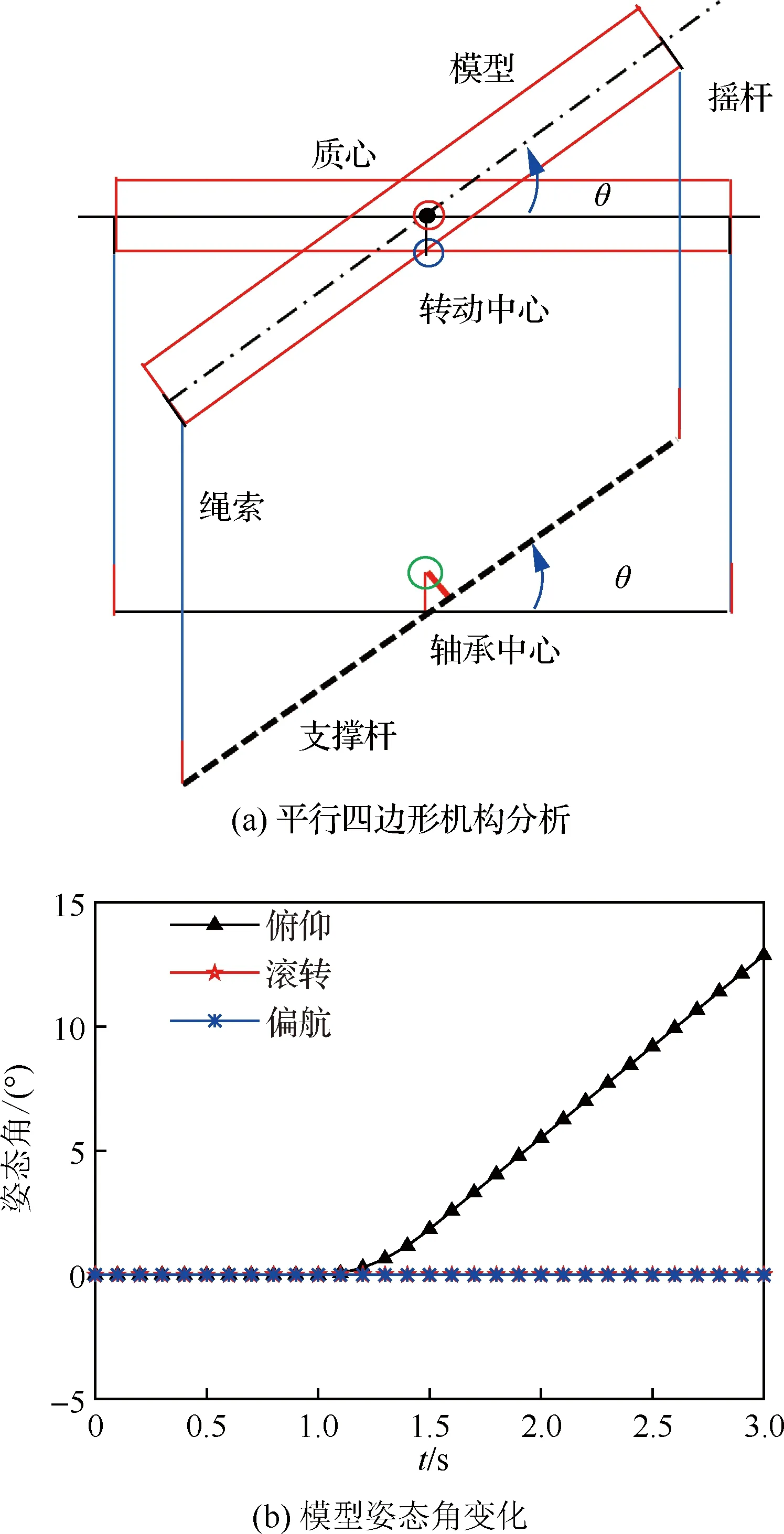
圖9 模型對稱面簡化為矩形(優化后)Fig.9 Model symmetry plane simplified as rectangle (after optimization)

3 運動學和動力學建模

本文所設計的飛行器模型繩系支撐機構屬于欠約束機構。在不改變初始繩長的條件下，模型在繩索支撐下，受來流和舵面力矩作用，實現模型在3個轉軸上的自由運動。飛行器模型做受迫運動時(例如舵偏作用時)，位姿不僅受繩索運動狀態的影響，還與該機構的動力學特性有關。

為驗證上述飛行器模型支撐機構的可行性，并預測飛行器模型在虛擬飛行試驗過程中的運動，對該機構進行飛行器模型的運動學和動力學建模。

3.1 運動學建模

首先建立牽引繩長度與飛行器模型位姿之間的運動學關系。

如圖10所示，在地面坐標系下，第根繩的繩長矢量為

=-=+--

(6)

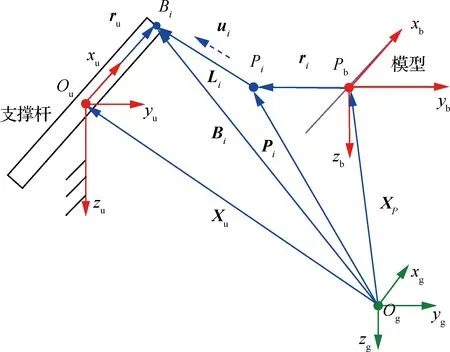
圖10 WDPR-VFT的運動學建模Fig.10 Kinematic modeling of WDPR-VFT

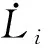
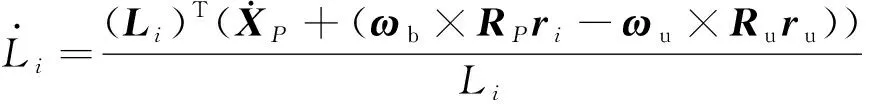
(7)

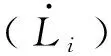
3.2 動力學建模

本文在飛行器模型無約束六自由度運動方程基礎上添加由4根繩索施加在模型機體上的約束力和約束力矩，同時考慮繩索的彈性阻尼和支撐桿轉動軸承的摩擦力矩，建立支撐桿繞桿件質心轉動的運動方程和有繩支撐約束下的飛行器模型動力學方程。

3.2.1 飛行器模型無約束六自由度運動方程

飛行器模型屬于六自由度運動體，基于動量定理、動量矩定理和哥氏定理可推導出模型無約束六自由度運動方程，鑒于篇幅原因，不在此詳細列出。

3.2.2 支撐桿繞其質心轉動的運動學/動力學方程

建立如圖11所示的坐標系，為建模方便，將機體重心初始位置設置在地面坐標系下的[0,0,-0.775] m，上桿坐標系的軸和機體坐標系的軸相互垂直，下桿坐標系的軸和機體坐標系的軸同向。

1) 繩索張力和軸承摩擦力矩建模

由于繩索受拉會產生彈性變形，十字架模型在運動過程中可能出現微小振蕩，對機構的穩定性產生一定的影響，因此，動力學建模考慮了繩索的彈性阻尼，其張力模型為

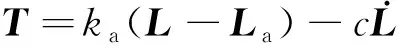
(8)

式中：為繩拉力矢量；為繩索剛度；為繩阻尼系數；為實時繩長矢量；為未變形的繩長矢量。本文采用直徑1.2 mm的Kevlar繩作為牽引繩，其彈性模量=43.9 GPa,=/=1.323× 10N/m，為繩索橫截面積。

上支撐桿轉動軸承的摩擦力矩模型為

=sgn()(+(-)e-||)+

(9)

式中：為庫侖摩擦力矩；為靜摩擦力矩；參數的引入使模型符合Stribeck效應；為黏性系數。

2) 繩索對模型的合力/力矩

4根繩索對機體產生的合力、合力矩為

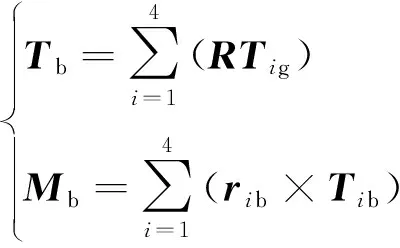
(10)

式中：g是第根繩索在地面坐標系下的繩拉力；是地面坐標系到機體坐標系的變換矩陣；b為第根繩索對應飛行器模型上的點在體軸系下的位置向量，=1,2,3,4分別表示圖11中上左繩、上右繩、下前繩、下后繩。

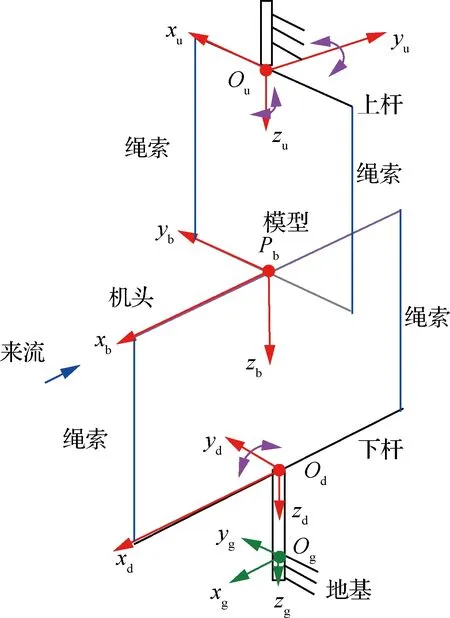
圖11 WDPR-VFT的動力學建模坐標系定義Fig.11 Dynamic modeling coordinate system definition of WDPR-VFT

3) 支撐桿所受合力矩

單根繩索對支撐桿在桿系坐標下的作用力矩為

u(d)=u(d)×u(d)

(11)

式中：u(d)是第根繩索對應上桿(下桿)上的點在桿系下的位置向量；u(d)是第根繩索在上桿(下桿)坐標系下的繩拉力。

上、下支撐桿所受合力矩和為

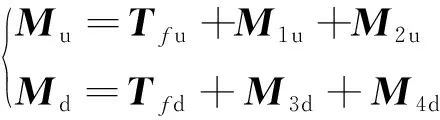
(12)

4) 支撐桿繞其質心轉動的運動學/動力學方程

上(下)支撐桿繞自身質心轉動的運動學和動力學微分方程為

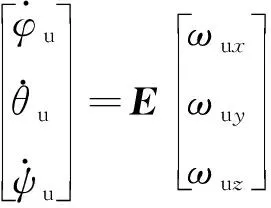
(13)

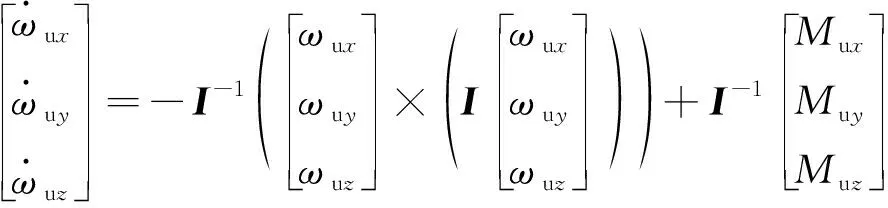
(14)

式中：、、表示上支撐桿的三軸姿態角；u、u、u表示上支撐桿的角速率沿3個坐標軸的分量；u、u、u表示上支撐桿所受合力矩在3個坐標軸上的分量；為歐拉轉換矩陣；為上支撐桿的轉動慣量矩陣。

3.2.3 繩索支撐約束下飛行器模型的運動方程

本文開展虛擬飛行試驗模型繩系支撐機構驗證試驗，采用圖5所示的飛行器模型，其氣動模型(氣動力和氣動力矩)從風洞試驗氣動數據庫和相關資料中收集并通過插值計算得到。

飛行器模型所受合力和合力矩為

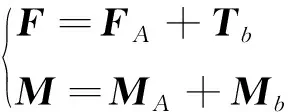
(15)

將飛行器模型所受合力和合力矩代入飛行器模型的無約束六自由度運動方程，可得繩索支撐約束下飛行器模型的運動學和動力學方程。

式(15)建立了有繩支撐約束下飛行器模型狀態量與舵面控制量之間的函數關系，以及上、下支撐桿的轉動角度、角速度與繩索拉力、軸承摩擦力矩之間的關系。

飛行器模型的位姿與繩長、繩拉力存在內在聯系，即對于本文設計的欠約束、可重構(牽引點時變)、被動驅動的繩系支撐機構，幾何運動方程和力平衡方程相互耦合，可通過聯合求解確定其相關參數。

4 仿真分析

為驗證上述飛行動力學建模的正確性和支撐機構的可行性，利用MATLAB中的Simulink模塊開展仿真分析。選取3種不同工況進行對比研究：模型無約束3自由度轉動運動(3DOF Unconstrained)；模型在有繩支撐約束下的無摩擦力矩的運動(WDPRVFT)；模型在有繩支撐約束下的有摩擦力矩運動(WDPRVFT+ Friction)。

4.1 數學模型穩定性

首先，初始化配平(配平迎角為2.1°)，在無舵偏角和風速情況下，給飛行器模型1°的抬頭俯仰角，繩索初始預緊力為50 N，仿真考察模型和俯仰支撐桿的變化情況。

如圖12所示，初始時刻飛行器模型在受到負的俯仰力矩作用下俯仰角減小，模型低頭向下，俯仰支撐桿(下桿)受正的俯仰力矩作用使其俯仰角增大，兩者在平衡位置來回振蕩，振幅不斷衰減，模型俯仰角最終穩定在0.79°，說明曲線趨勢是合理的，機構是穩定的，其中俯仰支撐桿振蕩幅值較大，與繩索預緊力和轉動慣量有關。

上述結果表明，由于繩索的彈性阻尼，機構運動過程中會產生微小的振蕩。但是很快就穩定下來。若通過機構絲桿組件中的移動副拉緊繩索，可以增大繩索的預緊力以減弱這種微小的振蕩。

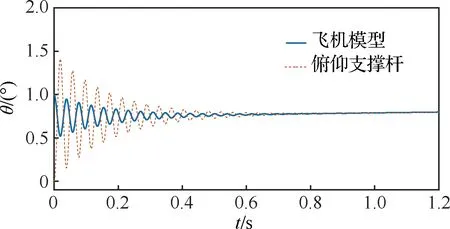
圖12 WDPR-VFT機構振蕩仿真Fig.12 WDPR-VFT mechanism oscillation simulation

4.2 典型縱向操縱響應

本文就WDPR-VFT的典型縱向操縱響應進行研究。選取典型縱向操縱輸入信號，即在來流風速為25 m/s條件下，待風速穩定后，輸入1°的升降舵階躍，階躍點在10 s處，升降舵的操縱響應結果如圖13和圖14所示。仿真結果說明飛行器模型對1°的升降舵階躍會產生負的純俯仰力矩，模型的俯仰角及其變化率在幾個來回振蕩后進入穩定狀態。

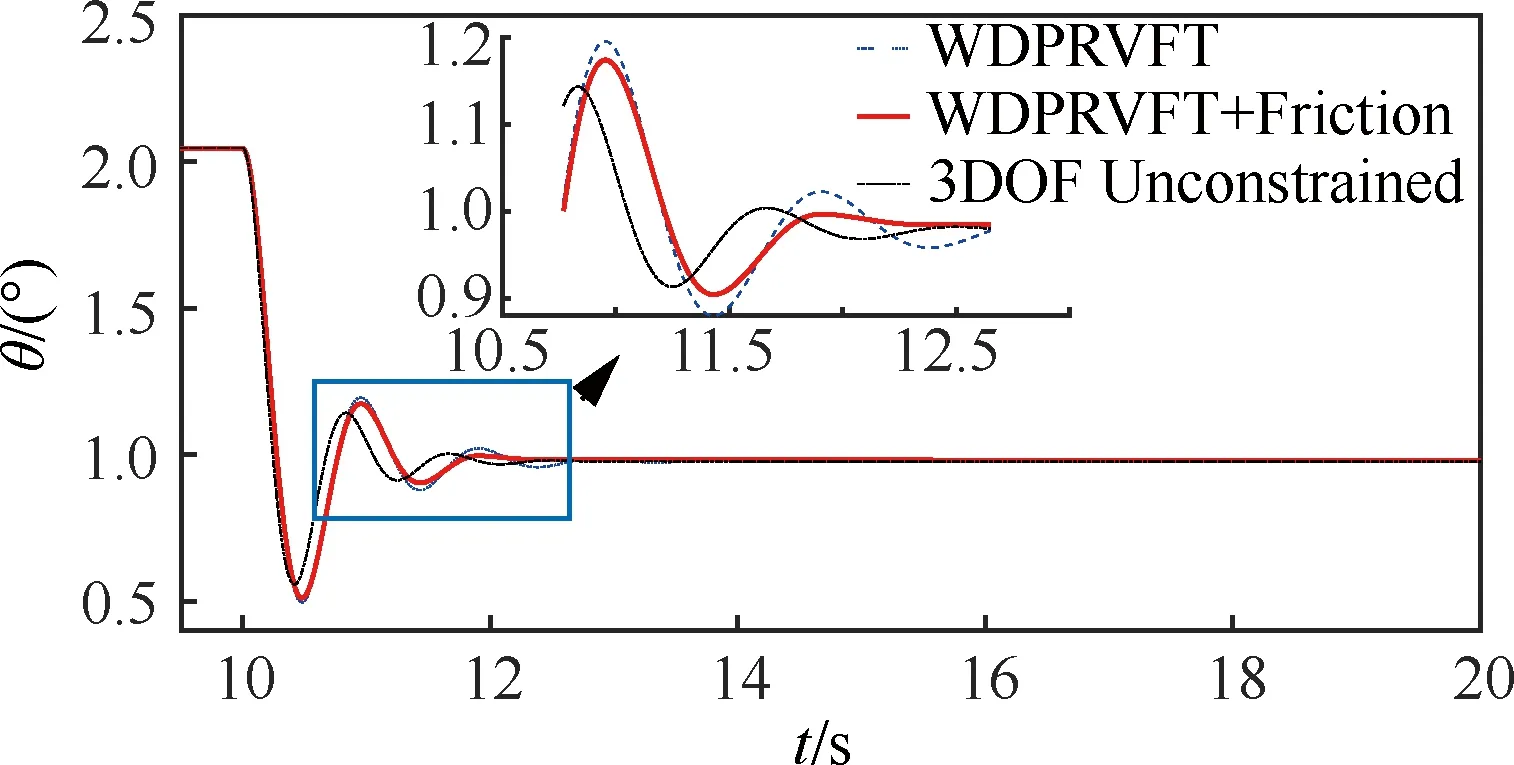
圖13 俯仰角變化Fig.13 Change of pitch angle

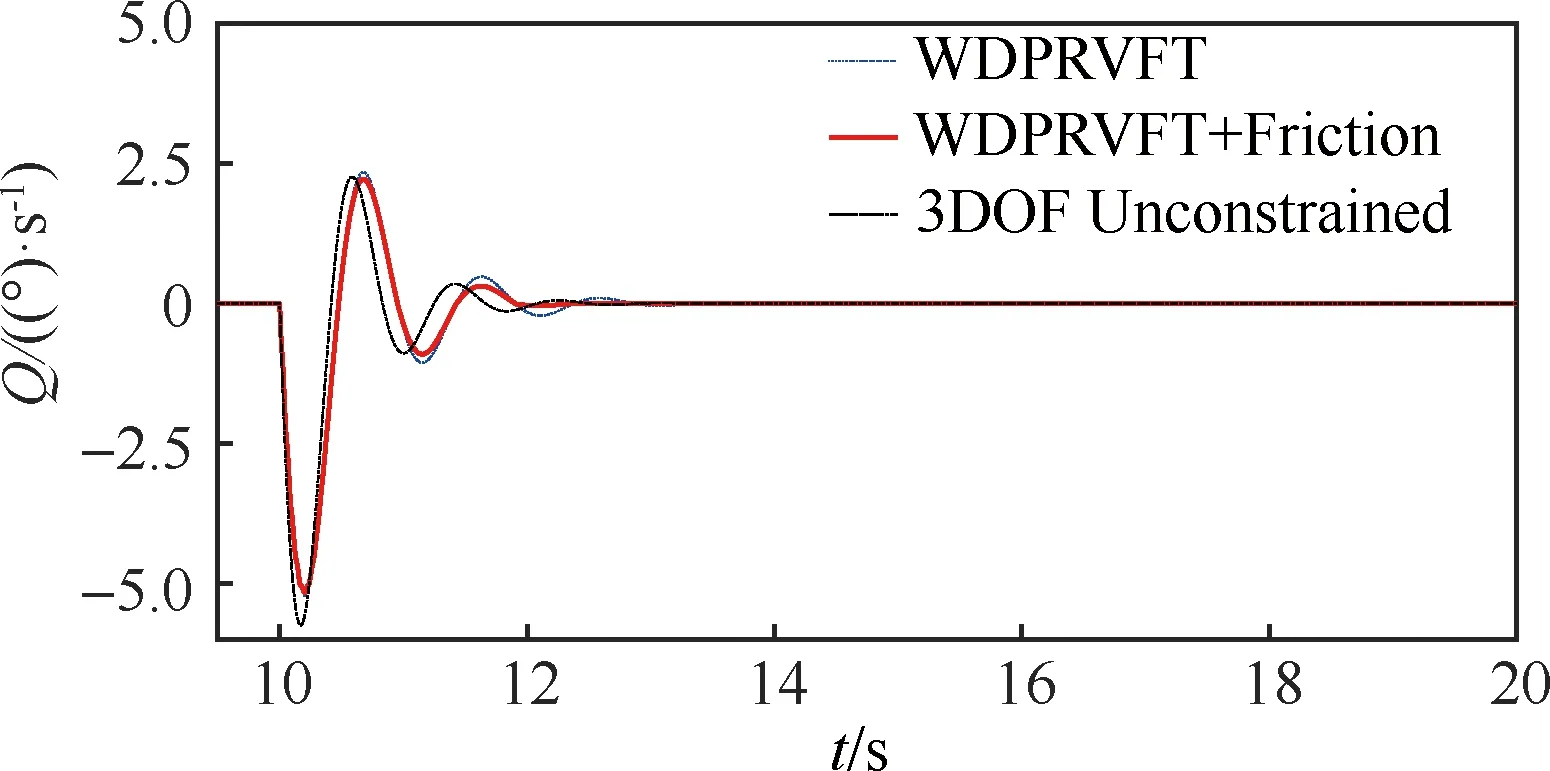
圖14 俯仰角速率變化Fig.14 Change of pitch angle rate

摩擦力矩會對模型的俯仰運動產生阻尼作用，阻尼使俯仰角變化速率峰值變小，在階躍后的第1個波峰處減小了0.12(°)/s，第2個波峰處減小了0.2(°)/s，并產生了死區現象，即在第2個波峰過零時(約在階躍后的1.92 s)不再振蕩，而是直接進入穩定狀態，比無摩擦力矩的結果提前約1.4 s。

與俯仰角變化速率對應，阻尼使俯仰角峰值在階躍后的0.96 s時減小0.03°，并在1.9 s后進入穩定狀態，與無摩擦的結果相比減小了0.04°。說明摩擦力矩對支撐機構的功能影響很小。

上述仿真結果說明本文設計的虛擬飛行試驗模型繩系支撐機構與模型無約束3自由度轉動仿真結果趨勢是一致的。由于摩擦力矩和繩索彈性的影響，WDPR-VFT模型并聯機構與無約束3自由度轉動相比，滯后約0.26 s。

在上述縱向操縱輸入下，模型的質心位移變化如圖15所示。圖15說明飛行器模型質心沿三軸的位移變化很小，沿機頭負方向的位移最大為0.016 mm，振蕩幅值越來越小并最終進入穩定狀態，說明該虛擬飛行試驗模型繩系支撐機構基本約束了飛行器模型的3個平動自由度，釋放了3個轉動自由度。

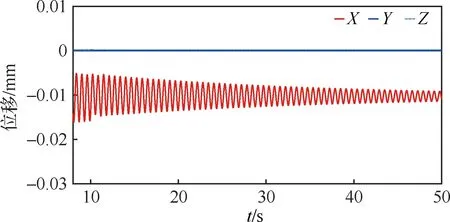
圖15 模型質心位移變化Fig.15 Displacement of model center of mass

上述分析結果表明，對于縱向操縱，WDPR-VFT模型支撐機構對飛行器模型運動影響很小，具有良好的自穩定性，驗證了動力學建模仿真結果的準確性，可以滿足風洞虛擬飛行試驗的需求。

5 試驗驗證

為驗證所設計的虛擬飛行試驗模型繩系支撐機構的可行性，在風洞里開展了俯仰單自由度試驗，即進行升降舵開環控制試驗，研究模型運動響應過程。

5.1 試驗設備

本文根據動力學相似準則，設計并加工了如圖16所示的帶舵面的試驗模型(具體尺寸參見圖5)，配置了開源飛行控制器Pixhawk、金屬齒數碼舵機等零件，用于模型姿態角測量和舵面控制，并將其安裝于實驗室的低速直流式風洞出口處，見圖17。

圖16 試驗模型及內部配置Fig.16 Experimental model and internal parts configuration

圖17 虛擬飛行試驗繩系支撐機構樣機Fig.17 Prototype of WDPR-VFT

該風洞試驗段橫截面為300 mm×300 mm，但對于圖16的模型來說顯得太小，故將模型放在風洞擴散段出口處，此處橫截面積為450 mm×450 mm，風速可達約30 m/s。但即便如此，由于風洞試驗條件限制，擴散段出口尺寸仍小于模型翼展。而且風洞擴散段后的流場也不太好，不是均勻流場，對試驗結果必然造成影響。

5.2 試驗結果

5.2.1 零舵偏時模型的縱向動態特性

驗證試驗在風洞來流速度10 m/s下進行。當對模型釋放俯仰單自由度后，在無舵偏的情況下，模型呈負的俯仰角，并出現小幅的俯仰阻尼振蕩，俯仰角繼續減小，最終穩定在平衡迎角處，如圖18所示。

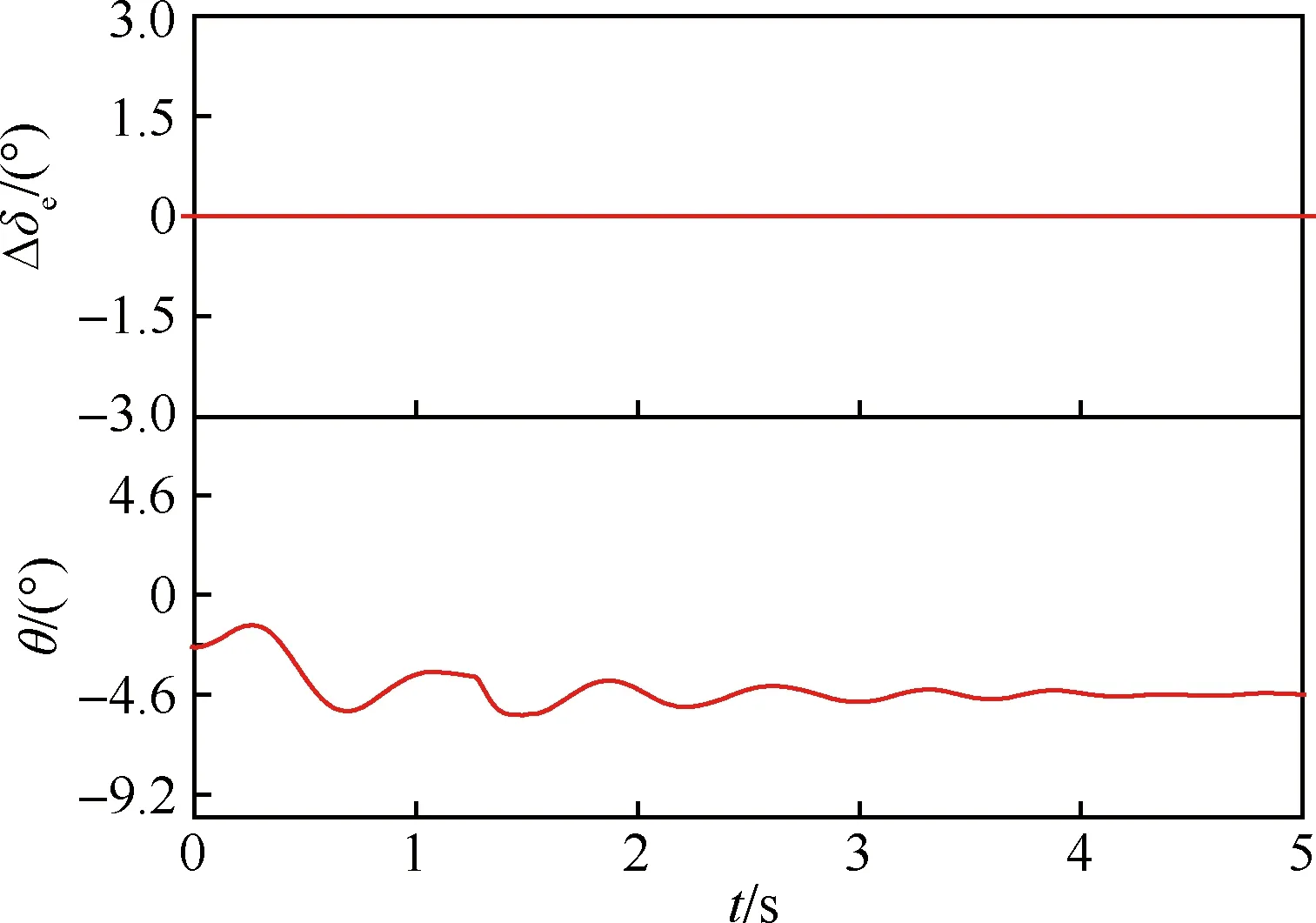
圖18 俯仰單自由度釋放后模型運動響應結果Fig.18 Model motion response after release of single pitch degree of freedom

課題組曾在在空氣動力研究院FL-5低速風洞以圖5的模型采用WDPR繩系機器人支撐和彎刀尾支撐進行吹風，得到過升降舵偏角為0°時的俯仰力矩系數對比試驗結果。另外，國內某氣動單位也對相同模型進行過吹風試驗。由以上風洞試驗結果可知，當=0°時，在=0°處，俯仰力矩系數<0，存在微小的低頭力矩。

因此，圖18中模型的俯仰角變化是合理的，符合該模型的氣動特性，也表明WDPR-VFT的縱向動態特性良好。雖然上述試驗是在風洞來流條件欠佳的情況下獲得，但從一個側面反映本文提出的WDPR-VFT支撐機構滿足風洞虛擬飛行試驗的基本要求。

5.2.2 俯仰短周期模態運動

圖19所示為用WDPR-VFT支撐模型吹風時的升降舵開環控制試驗曲線。模型在配平后進行升降舵階躍方波機動，激勵模型做俯仰短周期模態運動。試驗中，模型配平初始俯仰角為-4.5°，在第一個階躍方波機動中，升降舵從0°先往舵面負方向(即圖中Δ的正值方向)偏轉至10°，模型獲得抬頭的俯仰力矩，俯仰角升至22°左右并伴有小幅振蕩；升降舵再往舵面正方向(向下偏轉為正)偏轉至14°，模型獲得低頭的俯仰力矩，俯仰角降至-12°左右并伴有小幅振蕩后趨于穩定；最后再將升降舵回零，模型獲得抬頭的俯仰力矩，俯仰角回至0°附近。

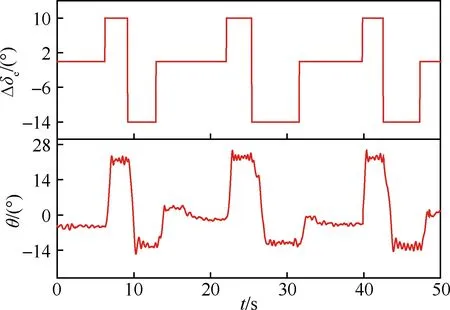
圖19 升降舵開環控制試驗曲線Fig.19 Open-loop control test curves in elevator maneuvering flight model test

階躍方波機動重復了3次，模型運動響應狀態基本一致。結果表明，圖5所示的動態試驗標模的升力特性明顯，升降舵往舵面負方向偏轉獲得的模型俯仰角變化比升降舵往舵面正方向偏轉獲得的模型俯仰角變化大得多。每次方波階躍機動后模型俯仰角都有一個小幅的振蕩并趨于穩定。這是由于模型的慣性與空氣阻尼相互作用的結果，也與典型縱向操縱仿真結果(見圖13)總體趨勢類似。

6 結 論

1) 運用螺旋理論對WDPR-VFT進行了構型設計和自由度分析，證明該機構可以實現飛行器模型3個轉動自由度的自由耦合和解耦運動，滿足風洞虛擬飛行試驗模型支撐的需求。

2) 對WDPR-VFT進行結構優化和穩定性分析，證明優化后的機構具有良好的穩定性。

3) 對WDPR-VFT建立了繩系欠約束、可重構、被動驅動機構的運動學和動力學的數學模型，并采用仿真方法分析在虛擬飛行試驗中的模型對典型縱向操縱的響應，結果表明WDPR-VFT模型支撐機構對飛行器模型運動影響很小，驗證了所建數學模型的可行性和有效性。

4) 在低速直流式風洞對WDPR-VFT機構的可行性進行了初步的試驗驗證，結果表明機構穩定性好，與典型縱向操縱仿真結果趨勢一致。

本文設計的用于風洞虛擬飛行試驗模型的繩系支撐欠約束機構WDPR-VFT，可為開展飛行器模型氣動/運動/控制一體化研究，探索飛行器模型氣動/運動耦合機理、開展模型氣動參數辨識提供條件，為風洞虛擬飛行試驗模型設計繩系支撐機構提供參考。