全陶瓷軸承外圈裂紋位置識別方法

石懷濤，劉子濛, ，白曉天,*，馬輝

1. 沈陽建筑大學 機械工程學院，沈陽 11016 2. 東北大學 機械工程與自動化學院，沈陽 110819

滾動軸承是航空發動機轉子系統的核心部分，其運行精度直接影響到航空發動機轉子的工作性能和使用壽命。因此，滾動軸承外圈故障也是導致航空發動機轉子系統發生故障的重要原因之一。在航空發動機大功率化和多功能化的發展趨勢下，其內部軸承-轉子系統結構也趨于復雜化與重載化。考慮到航空發動機對軸承運行精度和可靠性等方面的要求逐漸提高，全陶瓷球軸承以其優異的工作精度、高耐磨性和高承載能力，能夠適用于高速重載工況，在航空發動機中逐漸得到了應用。然而，工業陶瓷材料與軸承鋼材料相比，脆性更高，因此對故障更為敏感。全陶瓷球軸承外圈在發生早期裂紋故障時，初始微裂紋常以穿晶斷裂和晶間斷裂方式擴展，宏觀表現為脆性斷裂，導致故障發生更具突然性，對航空發動機轉子系統的工作性能影響更為劇烈。因此對全陶瓷球軸承外圈裂紋故障的檢測和診斷提出了更高的要求。

早期對滾動軸承外圈故障的研究主要集中在對故障發生形式的分析和對故障尺度的研究。全陶瓷球軸承外圈的早期故障形式主要分為剝落和裂紋，考慮到工業陶瓷材料的力學性能和軸承外圈的受載情況，相比于外圈剝落故障，外圈早期裂紋故障的發生對全陶瓷球軸承工作性能的影響更為嚴重。當全陶瓷球軸承外圈不同位置出現相同尺度的裂紋時，全陶瓷球軸承的運行精度和剩余壽命會出現很大的區別。因此，識別全陶瓷球軸承外圈裂紋的發生位置，可以更準確和更有效地揭示外圈早期裂紋故障對全陶瓷球軸承工作性能的影響，對航空發動機轉子系統的健康監測和壽命預測具有重要意義。

現有針對軸承外圈裂紋故障位置的識別方法主要分為動力學模型方法和數據分析方法。Petersen等分析了裂紋軸承外圈的載荷分布和時變剛度的變化，建立了確定裂紋位置的動力學模型。Qin等建立了基于耦合分段位移激勵的軸承外圈局部故障動力學模型，更準確地描述了軸承外圈發生局部故障時產生的位移沖擊激勵。Cui等提出了水平—垂直同步均方根方法(Horizontal-Vertical Synchronized Root Mean Square, HVSRMS)作為軸承外圈故障位置判定方法，通過數據分析的方法識別外圈裂紋故障的發生位置，同時考慮滾動體在經過外圈故障位置過程中與外圈的接觸力作用方向對水平—垂直同步均方根方法進行優化。Zhang等提出了一種基于核主成分分析(Kernel Principal Component Analysis, KPCA)和粒子群優化方法(Particle Swarm Optimization Support Vector Machine, PSO-SVM)的軸承外圈故障診斷方法。為準確診斷滾動軸承外圈故障尺度和發生位置，Wang等提出了一種基于定量映射模型(Quantitative Mapping Model, QMM)的滾動軸承定量定位故障診斷方法。上述研究在建立外圈裂紋故障動力學模型的過程中，沒有考慮到工業陶瓷材料與傳統軸承鋼材料裂紋產生機理的差異。此外，通過數據分析對外圈裂紋故障位置進行識別的方法大多是將外圈裂紋故障劃分至外圈上的某段區域，不能對外圈裂紋的發生位置進行準確識別。

考慮全陶瓷球軸承外圈早期裂紋故障的發生機理，結合外圈載荷分布，通過應變能變化的方法建立全陶瓷球軸承外圈裂紋故障動力學模型，考慮故障振動信號沿軸承外圈傳導過程中的振動衰減矩陣，建立全陶瓷球軸承外圈裂紋故障位置判斷模型，通過對外圈上兩不同位置的模擬振動信號的同步均方根差值進行分析，建立全陶瓷球軸承外圈裂紋故障位置識別方法。實驗數據表明，全陶瓷球軸承外圈裂紋故障位置識別方法能夠準確對全陶瓷球軸承外圈故障位置進行識別，為航空發動機用全陶瓷球軸承故障診斷、健康監測和壽命預測提供一定的理論依據。

1 動力學模型

1.1 外圈裂紋故障

如圖1所示，航空發動機角接觸球軸承在工作過程中承受沿徑向和軸向方向的聯合載荷作用，全陶瓷球軸承的內外圈在承受徑向和軸向載荷作用下對應的相對位移分別為和，將全陶瓷球軸承中受到載荷最大的滾動體的位置角定義為=0°，滾動體在運行至任意位置角時與全陶瓷球軸承內外圈的總接觸變形可以表示為

==sin+coscos

(1)

式中：為接觸角。=0°時，最大接觸變形量可以表示為

=sin+cos

(2)

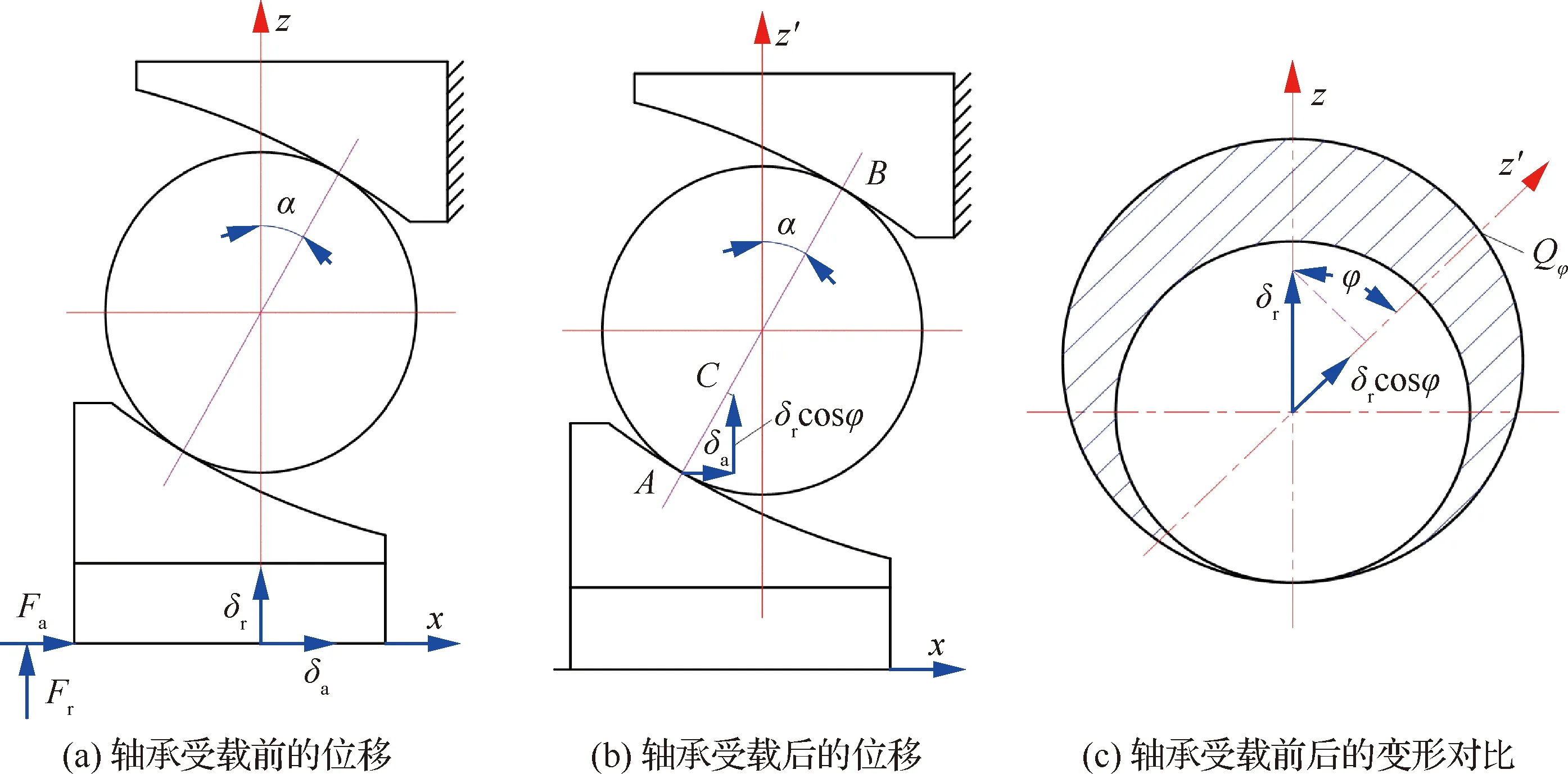
圖1 角接觸球軸承的位移與變形的關系Fig.1 Relationship between displacement and deformation of angular contact ball bearing

聯立式(1)和式(2)得到

(3)

式中：可以表示為

(4)

可得處于任意位置的滾動體所受載荷為

(5)

與傳統鋼制軸承外圈不同，全陶瓷球軸承外圈發生裂紋的主要形式是脆性裂紋，裂紋產生的主要原因是全陶瓷球軸承外圈受到沿滾道法向的剪切應力和循環應力作用下，全陶瓷球軸承外圈承受的連續低于材料疲勞極限的沖擊載荷而產生的脆性斷裂，同時，脆性斷裂可以表示為Ⅰ型張開型裂紋和II型裂紋相結合的復合形態裂紋。如圖2所示，將全陶瓷軸承外圈發生脆性斷裂進而產生的裂紋形式定義為翼型裂紋，也稱S型裂紋。

圖2 全陶瓷軸承外圈產生翼型裂紋示意圖Fig.2 Schematic diagram of wing crack on outer ring of full ceramic bearing

由脆性斷裂引起的翼型裂紋可分為兩部分：橫向裂紋導致的材料斷裂和縱向裂紋導致的外圈剛度削弱。對軸承外圈裂紋故障的研究主要討論翼型裂紋對軸承外圈剛度的削弱，因此主要針對縱向裂紋進行研究。考慮到外圈裂紋，特別是沿縱向發展的裂紋無法直接觀測和測量，通常采用估算方法。Lawn和Evans給出了裂紋深度與載荷分布和斷裂韌度之間的關系：

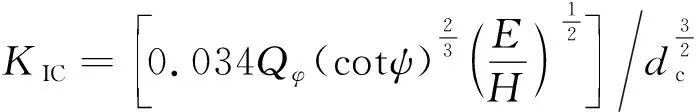
(6)

式中：為工業陶瓷材料的彈性模量；為維氏硬度，圖3為裂紋處截面示意圖，裂紋方向沿全陶瓷軸承外圈徑向方向；為裂紋張開角；為陶瓷材料在裂紋處的斷裂韌性。根據式(6)，可以得到陶瓷材料裂紋位置的斷裂韌性與裂紋尺寸之間的關系。

圖3 全陶瓷軸承外圈裂紋剖視圖Fig.3 Sectional view of crack on outer ring of full ceramic bearing

考慮裂紋的張開形式與裂紋產生原因，將沿徑向發展的全陶瓷球軸承外圈裂紋近似視為I型裂紋，應變能釋放率(Strain Energy Release Rate, SERR)與應力強度因子之間存在一定的函數關系。全陶瓷球軸承外圈在受到載荷作用下的應變能釋放率可以表示為

(7)

(8)

式中：為固有彈性模量。

由于裂紋擴展引起的外部作用轉矩是恒定的，因此在外圈上產生的最終應變能可以分解為無故障外圈的應變能與裂紋擴展產生的應變能之和：

=+Δ=+

(9)

式中：為裂紋擴展產生的能量；為無裂紋全陶瓷球軸承外圈的應變能。

全陶瓷球軸承外圈裂紋發生擴展時產生的應變能可以根據陶瓷材料斷裂力學表示為

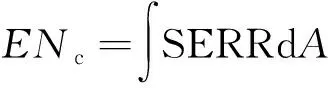
(10)

結合式(6)～式(10)，可得到外圈裂紋處時變剛度與外圈無裂紋處剛度的關系式：

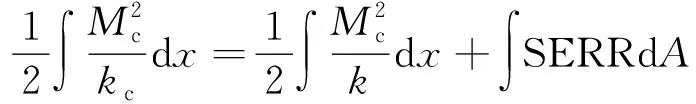
(11)

式中：為裂紋外圈的剛度；為無裂紋外圈的剛度；為外圈裂紋區域所受彎矩。可以得到裂紋對全陶瓷球軸承外圈剛度的削弱系數為

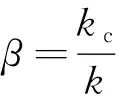
(12)

如圖4所示，結合外圈裂紋應變能釋放率、裂紋外圈載荷分布和時變剛度，建立了外圈裂紋故障動力學模型：

(13)

式中：為軸承的質量；和分別為滾動體與全陶瓷球軸承外圈的接觸剛度和阻尼，其計算方式參考文獻[24]，由式(5)得到。

圖4 外圈裂紋故障模型示意圖Fig.4 Schematic diagram of outer ring crack fault model

1.2 位置判斷

對含外圈裂紋故障的全陶瓷球軸承動力學模型進行仿真計算，得到的故障振動信號可以看作是發生在軸承外圈裂紋位置處的故障振動信號。從全陶瓷球軸承外圈裂紋故障位置處產生的故障振動信號沿外圈傳導至外圈上不同位置的過程中會發生不同程度的振動衰減。因此，選取軸承外圈上相連經過軸承中心的兩個位置，對兩位置上的故障振動信號進行測量和分析，即可對軸承外圈發生裂紋故障的位置進行一定程度的識別。

振動信號測點示意圖如圖5所示，外圈上點處為軸承外圈早期裂紋故障的發生位置，裂紋位置角可以表示為，在此位置外圈裂紋故障所引起的故障振動信號為()。選取和兩點作為外圈故障位置分析的兩個位置，定義和兩點連線經過軸承中心且垂直于軸承外圈所受到的徑向載荷方向。本研究僅對發生在全陶瓷球軸承外圈受到徑向載荷作用的半圈內發生的早期裂紋故障位置進行識別，故障振動信號沿全陶瓷球軸承外圈傳導至外圈上和兩點，定義故障振動信號()沿軸承外圈傳導至和位置處的故障振動信號分別為()和()，假設傳遞介質僅為軸承外圈，同時將軸承外圈視為均勻剛度—阻尼介質。

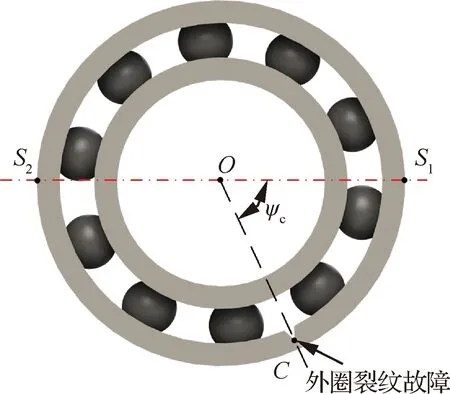
圖5 振動傳感器在外圈測點位置示意圖Fig.5 Schematic diagram of measuring point position of vibration sensor in outer ring

根據外圈早期裂紋故障的發生位置和故障振動信號傳導至外圈上的位置，將故障振動信號傳導路徑上的軸承外圈劃分為若干段區域。將被劃分的外圈各區段均視為剛度阻尼系統，故障振動信號傳導至外圈上的兩點和可視為等質量質點。將含外圈裂紋故障的全陶瓷球軸承動力學模型改進為軸承外圈裂紋故障位置識別動力學模型。改進后的全陶瓷球軸承外圈裂紋故障位置判斷動力學模型可以表示為

()+()-()+

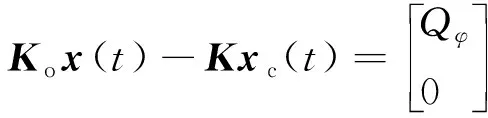
(14)

式中：()為軸承外圈上兩點位置和的狀態向量，可以表示為

(15)

()為外圈裂紋故障位置的狀態向量，其表達式為

(16)

為質量矩陣，其表達式為

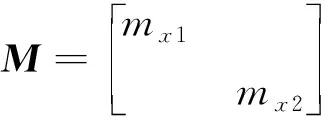
(17)

將和兩位置之間非受載區段的無裂紋外圈半圈、從位置到外圈早期裂紋發生位置的外圈區段和外圈早期裂紋發生位置到位置之間的外圈區段的剛度分別定義為0、1和2，對應的阻尼系數分別定義為0、1和2。

將全陶瓷球軸承外圈信號傳導過程中的剛度視為故障振動信號沿軸承外圈傳導過程中克服的彎曲剛度，考慮外圈各區段的剛度和阻尼，建立裂紋故障位置處產生的故障振動信號沿外圈傳導過程的衰減矩陣。其中，和分別為故障振動信號沿外圈傳導的衰減剛度和阻尼矩陣，其表達式分別為

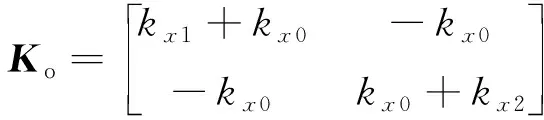
(18)

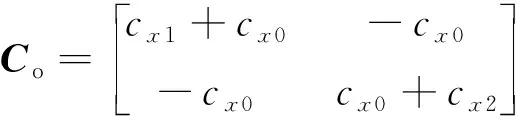
(19)

和分別為外圈傳導剛度和阻尼矩陣，其表達式分別為

(20)

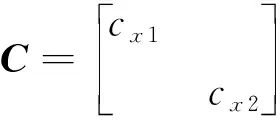
(21)

傳導剛度(=0,1,2)可表示為

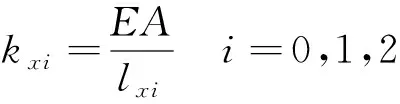
(22)

式中：為全陶瓷球軸承外圈的橫截面積；為對應軸承外圈的弧長。

則衰減阻尼矩陣可以表示為

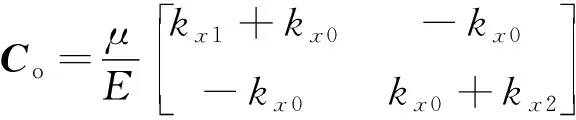
(23)

(24)

式中：為陶瓷材料的粘滯系數。

2 外圈裂紋故障位置判斷

2.1 仿真結果與分析

通過MATLAB和Simulink仿真計算，采用四階Runge-Kutta法求解外圈裂紋故障判斷動力學模型，步長Δ=2·10s。模型仿真計算選用的軸承型號為全陶瓷球軸承7004AC角接觸球軸承，選取軸承徑向力=50 N，在仿真計算過程中，為避免其他因素對裂紋位置判斷造成干擾，僅選取軸承外圈裂紋位置作為唯一變量。外圈裂紋深度選取0.35 mm，裂紋開口角度選取0.5°，不考慮裂紋故障擴展過程，僅對在此裂紋尺寸狀態下的外圈裂紋故障進行位置識別。圖6是通過式(14)仿真計算獲得的故障振動信號。

圖6 φc=0°時外圈S1和S2處模擬故障振動信號Fig.6 Simulated fault vibration signal of outer ring S1 and S2 in state φc=0°

通過對外圈裂紋故障判斷動力學模型進行仿真計算，可以得到軸承外圈和兩位置的故障振動時域信號()和()。通過故障振動信號可以看到，當滾動體運行經過外圈裂紋位置過程中，會導致軸承運動響應產生沖擊性振動，通過兩故障振動時域曲線的沖擊振幅可以判斷出外圈裂紋位置角處于=0°～90°區域內。

2.2 判斷方法

兩位置的故障振動時域信號的同步均方根差值(Synchronous Root Mean Square, ΔSRMS)設定為

ΔSRMS=SRMS1-SRMS2

(25)

式中：SRMS1和SRMS2分別為振動時域信號()和()的同步均方根。

圖6為軸承外圈上和兩位置在裂紋位置角=0°狀態下的故障振動時域信號()和()。圖7為兩故障振動時域信號同步均方根差值隨軸承外圈裂紋位置角變化的變化情況。如圖7所示，當外圈裂紋位置角=0°時， ΔSRMS為最大值。當外圈裂紋位置角從=0°變化到=90° 的過程中，ΔSRMS逐漸減小為0，當外圈裂紋位置從=90°變化到=180°的過程中，ΔSRMS繼續減小直到達到最小值。因此可以得到外圈上和兩位置上故障振動信號()和()的同步均方根差值和外圈裂紋故障位置角之間的映射關系。

圖7 同步均方根差值隨外圈裂紋位置角φc的 變化情況Fig.7 Variation of (SRMS with outer ring crack position angle φc

從圖7可以看出，ΔSRMS與外圈裂紋角的二次方有近似的映射關系。根據和兩位置處的故障振動信號()和()的ΔSRMS，可以推導得到全陶瓷球軸承外圈裂紋故障位置角與ΔSRMS之間的近似函數關系：

(26)

式中：為軸承外圈裂紋位置判斷方法的修正系數，通過對外圈裂紋故障位置判斷模型進行仿真計算后得到的參數代入式(26)獲得。

考慮到進行仿真計算時選取的步長與軸承轉速，可以得到通過外圈裂紋位置判斷模型進行分析的時間間隔為Δ，因此通過全陶瓷球軸承外圈裂紋位置判斷方法識別外圈裂紋故障位置角的精度可表示為

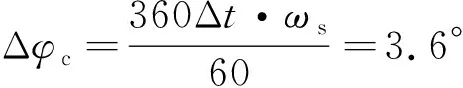
(27)

綜上所述，全陶瓷球軸承外圈裂紋故障位置判斷方法流程圖如圖8所示。

圖8 全陶瓷球軸承外圈裂紋故障位置判斷 方法流程圖Fig.8 Flow chart of recognition method for crack position angle of outer ring of full ceramic ball bearing

3 位置判斷實驗

通過對實驗數據的分析，驗證所提出的全陶瓷球軸承外圈裂紋位置判斷方法的準確性和可行性。圖9為本實驗中使用的軸承轉子實驗臺。

圖9 軸承轉子試驗臺Fig.9 Bearing rotor test bench

將7004AC全陶瓷角接觸球軸承安裝在軸承故障試驗臺上，實驗的主要參數見表1。其中一個全陶瓷球軸承的外圈通過加工得到裂紋故障；裂紋故障軸承的安裝位置和角度如圖10所示。外圈裂紋的位置角從=0°到=180°之間變化。

表1 全陶瓷球軸承外圈裂紋位置判斷實驗參數

圖10 全陶瓷球軸承外圈裂紋故障位置判斷實驗Fig.10 Experimental on location of crack in outer ring of full ceramic ball bearing

3.1 實驗與仿真比對

考慮到研究對象為外圈早期裂紋故障，裂紋深度分別選取0.30、0.35 mm和0.40 mm。將所測得外圈不同深度裂紋故障的實驗結果與全陶瓷球軸承外圈裂紋故障位置判斷動力學模型的仿真信號進行對比，如圖11所示。

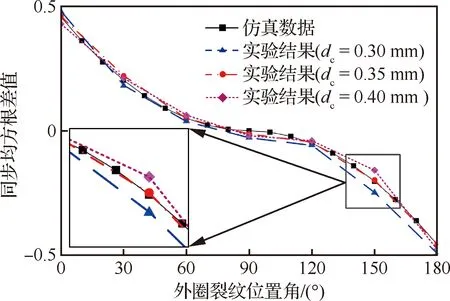
圖11 全陶瓷球軸承外圈裂紋位置判斷模型的 仿真與實驗對比Fig.11 Simulation and experimental comparison of crack location recognition model for outer ring of full ceramic ball bearing

從圖11可以看出，ΔSRMS的實驗結果從= 0°到=180°的過程中呈遞減狀態，同時，ΔSRMS在=90°狀態下約為0。考慮到實驗中的干擾等問題，可以看到實驗得到的外圈裂紋位置角-ΔSRMS曲線高度一致，證明了所提出的全陶瓷球軸承外圈裂紋故障位置判斷動力學模型的準確性。

3.2 外圈故障位置判斷示例1，φc=30°

外圈裂紋位置角設置為=30°，在軸承外圈和兩位置處設置2個傳感器，裂紋深度為=0.35 mm，裂紋張開角為=0.5°。實測在此狀態下全陶瓷球軸承外圈發生裂紋故障的振動信號，圖12為外圈裂紋位置角=30°時，和兩位置處的故障振動信號()和()。

圖12 外圈S1和S2處實驗故障振動信號(示例1)Fig.12 Experimental vibration signal at outer ring S1 and S2(Example 1)

根據外圈裂紋故障位置判斷方法，對全陶瓷球軸承外圈的裂紋位置角進行了分析和識別：

分別計算兩故障振動信號()和()對應的同步均方根SRMS1和SRMS2。對兩信號的同步均方根差值進行了計算，根據式(25)，得到同步均方根差值：

ΔSRMS=SRMS1-SRMS2=025

(28)

通過得到ΔSRMS的值，根據全陶瓷球軸承外圈裂紋故障位置判斷方法，通過全陶瓷球軸承外圈裂紋位置角進行分析：

=3102°

(29)

通過全陶瓷球軸承外圈裂紋故障位置判斷方法得到的外圈裂紋位置角與設定外圈裂紋故障的位置角的誤差為1.02°，在誤差允許范圍內。

3.3 外圈故障位置判斷示例2，φc=150°

外圈裂紋位置設置為=150°，在軸承外圈和兩位置處設置2個傳感器，裂紋深度選取=0.35 mm，裂紋張開角選取=0.5°。實測在此狀態下全陶瓷球軸承外圈發生裂紋故障的振動信號，圖13為外圈裂紋位置角=150°時，和兩位置處的故障振動信號()和()。

圖13 外圈S1和S2處實驗故障振動信號(示例2)Fig.13 Experimental vibration signal at outer ring S1 and S2(Example 2)

根據外圈裂紋位置識別方法，對全陶瓷球軸承外圈的裂紋位置進行了分析和識別。分別計算兩故障振動信號()和()對應的同步均方根SRMS1和SRMS2。對兩信號的同步均方根差值進行了計算，根據式(25)，得到同步均方根差值：

ΔSRMS=SRMS1-SRMS2=-021

(30)

通過得到ΔSRMS的值，根據全陶瓷球軸承外圈裂紋故障位置判斷方法，通過全陶瓷球軸承外圈裂紋位置角進行分析：

=14926°

(31)

通過全陶瓷球軸承外圈裂紋故障位置判斷方法得到的外圈裂紋位置角與設定外圈裂紋故障的位置角的誤差為1.02°，在誤差允許范圍內。結果表明，全陶瓷球軸承外圈裂紋故障位置判斷方法適用于全陶瓷球軸承外圈早期裂紋故障的位置判斷。

4 結 論

1) 全陶瓷球軸承外圈不同位置裂紋產生故障振動信號沿外圈傳導過程中會發生振動衰減，分析外圈上兩不同位置處的故障振動信號，得到兩故障振動信號同步均方根差值與裂紋故障位置角之間的函數關系，建立外圈裂紋故障位置判斷方法。

2) 將傳感器設置于相連通過軸承中心的外圈上兩位置，將實測得到的故障振動信號與外圈裂紋故障位置判斷模型的仿真結果進行對比，結果證明外圈裂紋故障位置判斷模型的準確性。

3) 通過外圈裂紋故障位置判斷方法對預設位置故障進行位置識別，結果證明外圈裂紋位置判斷方法的可行性。實驗結果與仿真計算結果吻合度較好，表明本方法對陶瓷軸承外圈裂紋定位效果較好，定位精度為3.6°。