打破思維定式 感悟代數思想
——“認識方程”教學案例研究
安徽碭山縣實驗小學(235300)房天營
【案例背景】
方程是小學階段培養學生代數思想的重要載體,是學生由算術思維邁向代數思維的起點,所以方程在小學階段具有極其重要的地位。方程是學生在經歷了用字母表示數的過程,并且會尋找數量之間的等量關系的基礎上學習的。然而,無論是用字母表示數,還是尋找數量之間的等量關系,對學生而言都是很抽象的,他們一下子很難接受代數思維,所以教學的難度很大。
【教學內容分析】
“認識方程”這節課的重點是要學生結合具體情境了解方程的意義,會用方程表示情境中的等量關系,并且經歷將現實問題抽象成等式與方程的過程,學生在學習的過程中將積累等量關系符號化的活動經驗。為了使學生體會方程是刻畫現實世界的一個數學模型,激發學生的學習興趣,教材編排了三個情境(如圖1-1、1-2、1-3)和三個問題:
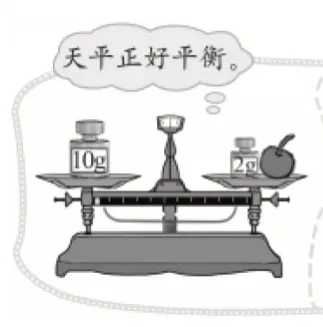
圖1-1
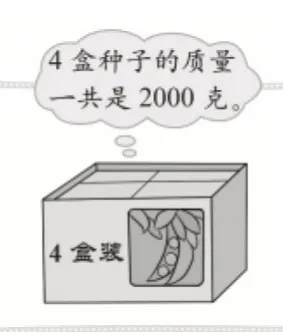
圖1-2

圖1-3
第一個問題是用口頭語言描述上述情境中的等量關系(如圖2)。

圖2
第二個問題是引入“用字母表示數”,引導學生用式子表示情境中的等量關系(如圖3)。
第三個問題是觀察上面表示等量關系所用的式子,抽象并概括出共同特征,從而認識方程(如圖4)。

圖4
【教學回放】
師(出示圖1-1):估一估櫻桃的質量。
生1:我估計大約有10克。
生2:我估計大約有30克。
師:你們說的都是具體的數量,能不能用字母來表示櫻桃的質量?
生3:櫻桃的質量是n克。
生4:櫻桃的質量是x克。
……
出示:
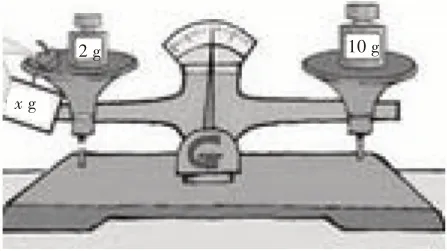
圖5
師:根據這幅圖說一個式子。
生5:櫻桃的質量+小砝碼的質量=大砝碼的質量。
師:現在櫻桃的質量是x克,能列出一個式子嗎?
生6:x+2=10。
[教學思考:借助天平直觀演示平衡,說明兩邊物體的質量相等,學生說出等量關系后很容易列出等式。由實物演示到抽象式子的過程,學生的思維能力得到進一步發展。]
出示圖6:

圖6
師:觀察情境圖,說出圖中的數量關系。
生7:4塊月餅的質量=380克。
生8:每塊月餅的質量×4=380克。
生9:380÷4就等于每塊月餅的質量。
師:如果每塊月餅重y克,能列出一個等式嗎?
生10:380÷4=y。
師(有點著急):沒錯,這是一個等式,但不是根據“每塊月餅的質量×4=380克”來列的,還可以怎么列?
(學生沉默)
師:看黑板上的式子“每塊月餅的質量×4=380克”,左邊是什么?右邊呢?怎么列式?
生11:y×4=380。
出示:4塊月餅的質量=380克
4y=380
[教學思考:由天平過渡到電子秤,形式的變化使學生失去了直觀的兩端相等的參照,陷入了用算術法計算結果的慣性思維當中。盡管教師一再啟發、提示,但學生由于沒有學習方程,始終很難想到用方程式子表示等量關系。]
出示課本情境圖:
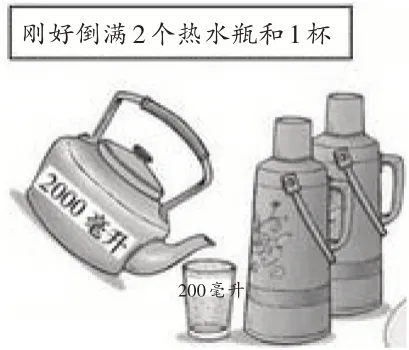
圖7
師:看到這幅圖,你會列式嗎?
生12:(2000-200)÷2。
師:為什么這樣列式?
生12:這樣可以算出每個熱水瓶能裝900毫升水。
師:我們不需要計算出結果,只需要表示它們之間的相等關系。2個熱水瓶的容量和1個水杯的容量正好是水壺的容量,應該怎樣列式?
生13:2個熱水瓶的容量+1個水杯的容量=水壺的容量。
師:如果每個熱水瓶的容量是n毫升,怎樣用式子表示?
生14:2×n+200=2000。
生15:2n+200=2000。
(教師根據板書的算式分類、歸納,揭示方程的概念。然而在練習環節,學生依然出現了“不列方程,而用算術方法直接算出結果”的現象。)
[教學思考:用語言表達等量關系本身就是教學的難點,更何況是這么復雜的等量關系,學生不能順利說出等量關系也是意料之中。但教師沒有更好的辦法引導學生感受順向思維的優勢。]
出示圖8:
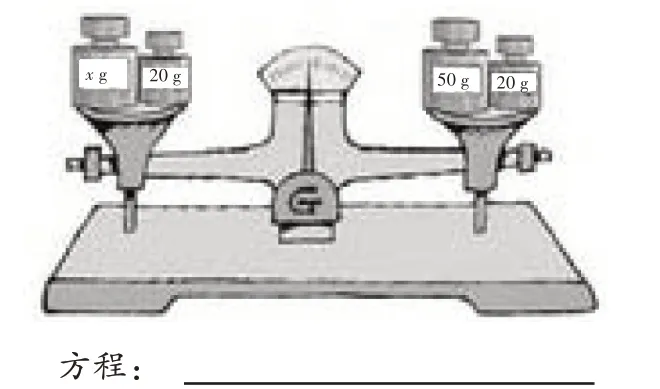
圖8
生16:x+20=20+50。
出示圖9:
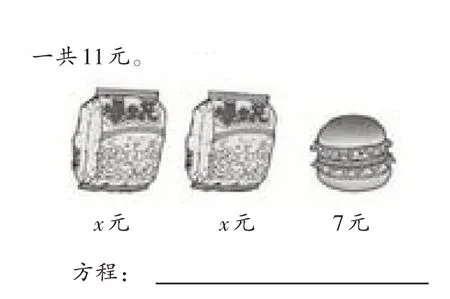
圖9
生17:(11-7)÷2=x。
(有的學生干脆直接算出了結果)
【案例研討】
在議課環節,評課教師給出了積極的評價:執教者語言幽默詼諧,尤其是肢體語言極為豐富,課堂上笑聲不斷,給學生營造了一個愉快的學習氛圍;這節課的教學設計樸實而有新意,教學過程真實而生動,學生學得輕松又愉快。但是也提出了存在的問題:在揭示方程概念時,學生列方程表示的式子始終沒能達到要求,雖然這是學生真實的學習狀態,但是顯然沒有達到預期的教學效果。
學生在表示情境圖中的等量關系時為什么不會順向思維用方程表示,非得逆向思維用算術方法計算出結果呢?如何解決這一問題?
【案例分析及思考】
帶著這個問題,筆者認真查閱了相關資料并積極和教研組的教師進行了探討,得出以下幾個方面的因素。
1.學生的思維定式。用算術方法計算結果是學生多年的習慣,因為從小學一年級開始,面對問題時,教師常這樣提問:“要想求出這個問題,我們該怎么計算?”算術法已經成為學生的慣性思維,因而與新知造成沖突。而學生的認知與經驗發生沖突,正是學習新知的一個契機,也是學習新知的增長點。對此,教師首先應認可等式380÷4=y,再引導學生利用字母表示數的知識進行討論,最后得出4y=380。這樣,先讓學生明白同樣的等量關系可以用不同的等式表達,再引導學生比較這兩個等式哪個更好,更符合思維習慣。學生經過比較后也會得出“4y=380更好理解”的結論。
2.學生對于用字母表示數量和把字母當成已知數量參與運算不習慣。因為有了前一節的用字母表示數的認知基礎,本節課的教學如果要充分鏈接舊知識,在涉及從數量等式到含有字母的等式時,就需要適當過渡一下。如一開始的天平平衡,兩邊都放入已知的砝碼,左邊放2個5克砝碼,右邊放一個10克砝碼,讓學生得出5+5=10,然后把一個砝碼換成一個實物,假設它有x克,引導學生寫出5+x=10。這樣強化等量關系和等式的概念,便能喚醒學生的舊知,學生就能夠從生活情境中提煉出方程模型,并用含有未知數的等式來表達等量關系。
3.學生處在由具體形象思維到抽象思維的過渡時期。用天平演示時,學生很容易得出等量關系,并列出方程,而對于隱藏了天平的實物或圖片,學生則不容易列出方程。這就充分說明了具體形象的東西,學生容易理解和接受,而對于需要進行分析和推理的概念,學生則難以接受和領悟。對此,可充分利用多媒體和各種直觀的實物教具,先帶領學生對等量關系及等式進行有目的地觀察,讓學生從具體的形象中區分哪些是主要的,哪些是次要的,找出它們之間的內在聯系,再用形象生動的語言啟發他們比較、分析和判斷,找出其中的相同點和不同點,再歸納概括出等量關系與等式之間的本質屬性,學生就能從形象思維過渡到抽象思維,列方程就會更加順利。
4.提出的問題指向不明確。在出示4塊月餅重380克的情境圖之后,教師提出:“觀察情境圖,說出圖中的數量關系。”接著又問:“如果每塊月餅重y克,能列出一個等式嗎?”這樣的問題指向不夠明確,學生的思考也就沒有目的性。這里的問題可以更具體些,例如改成“根據情境圖,我們可以找到一個等量關系,寫出一個等式,那么在圖中你還能找到另一塊等量關系嗎?”這樣學生就能容易地說出“4塊月餅的質量=380克”。教師再啟發學生分析“當一塊月餅的質量未知時,我們可用字母x或y表示,那么能得出一個什么樣的等式呢?”這樣的引導更自然,學生用方程來表示也會水到渠成。
總之,教學方程知識,教師要根據教學內容和學生的思維水平,運用恰當的教學方法,提出切實可行的要求,對學生進行代數思維的初步訓練。只有這樣,才能讓學生感悟和接受方程思想,從而與初中數學的學習接軌。“教學永遠是一門遺憾的藝術”,但只要教師靜下心來思考,蹲下身體了解學生,深度把握細節,有效突破難點,就會讓課堂精彩而高效,也會讓遺憾少一些。

