非厄米線性響應理論及其應用*

潘磊

(清華大學高等研究院,北京 100084)

線性響應理論是現代物理實驗尤其是量子物態測量實驗的理論基礎,其核心是將物理系統的探測信號作為微擾,利用系統在未受擾動時的關聯函數來刻畫物理可觀測量的響應.半個多世紀以來,基于封閉量子系統的線性響應理論在量子物態測量實驗上取得了巨大的成功.隨著超冷原子實驗在光場與系統相互作用精確操控方面的快速進展,近年來高精度的冷原子實驗已經具備研究耗散量子多體系統的條件,新奇的物理現象在實驗中層出不窮,這使得國內外研究者對量子開放系統及其非厄米物理的研究與日俱增.基于此,我們發展了一個量子開放系統的線性響應理論—非厄米線性響應理論.該理論將耗散帶來的非厄米效應與量子噪聲作為外部探測輸入來探測量子系統的性質,并將實驗可觀測量的含時演化與系統未受擾動狀態時的關聯函數及其譜函數聯系了起來,提供了區分正常物態和奇異物態的一種新手段,所得到的結果與最近冷原子系統實驗的結果高度吻合.本文介紹了非厄米線性響應理論,并討論該理論在量子多體系統以及具有時間反演對稱性的量子系統中的應用.

1 引言

非平衡態物理尤其是非平衡態動力學是物理學中古老而經久不衰的研究主題.在量子系統中有兩類典型的非平衡動力學過程: 一類是封閉系統的非平衡動力學,此類過程描述的是系統本身從非平衡態弛豫到平衡態的動力學演化;另一類是開放系統中的量子耗散動力學,此類過程描述的是一個與環境熱庫相互作用的量子系統趨于穩態的動力學演化.與平衡態物理不同,量子多體系統中的非平衡動力學演化原則上涉及系統所有的自由度,這使得量子多體非平衡動力學成為當今物理學中的一大挑戰.近年來,得益于冷原子實驗在精密計時技術與測量手段方面的進步,高精度的冷原子實驗已經具備了研究封閉系統和開放系統的非平衡動力學的條件,并發現了許多新奇的物理現象,冷原子系統逐漸成為非平衡動力學方面研究的理想平臺[1—10],也使得量子耗散及其非厄米物理在近幾年來受到國內外研究者越來越多的研究與關注[11,12].通過對外部光場與系統耦合的精確操控,實驗上成功實現了諸多量子開放系統,并測量了幾種典型的量子耗散動力學演化,為非平衡動力學的理論研究提供了新的機遇和挑戰.2020 年,法國巴黎高師Brossel 實驗室的Gerbier 研究組[13]通過精確調控激光場與光晶格系統中玻色子的耦合,研究了二維Bose-Hubbard 模型在不同相互作用強度下的兩體耗散動力學,他們發現隨著粒子之間相互作用的增強,在動量分布的寬度變化中出現了亞擴散(subdiffusion)現象,并且在動量分布峰值的演化中出現了反常的非指數衰減行為.針對這些新奇的實驗現象,基于量子物態實驗中廣泛運用的線性響應理論,我們提出了將耗散作為外部輸入的量子開放系統版本的響應理論,并將其命名為“非厄米線性響應理論”[14].

本文首先對非厄米線性響應理論做簡單介紹,然后利用該理論解釋耗散二維Bose-Hubbard 模型中的實驗現象,給出一維相互作用量子氣體中的預言,并應用于具有時間反演對稱性保護的量子系統.

2 非厄米線性響應理論簡介

測量一個系統的物理性質時,通常的做法是給待測系統施加一個擾動,然后探測系統對擾動是如何響應的.這個外加的擾動強度在能夠觀測到信號的前提下要盡量小,以保證系統本身的物理性質不被破壞.線性響應理論的精神就在于此.設系統在外場作用下的總哈密頓量為

這就是線性響應理論的公式[15],也稱為久保公式(Kubo formula).(5)式表明,近似到外場擾動的線性階,系統的響應正比于推遲格林函數G(t,t′)=.線性響應理論是實驗測量的基礎,它的重要意義在于從系統中測量到的響應被包含在了系統的關聯函數中.這種關聯在量子物態的測量中尤為顯著.常見的譜學測量,如非彈性中子散射信號由系統的自旋-自旋關聯函數決定;而輸運測量,如電導的測量由流-流關聯函數決定等[16].以上是傳統的針對封閉系統的線性響應理論,現在介紹非厄米線性響應理論.對于一個與環境自由度耦合的開放系統,其受到的影響不再是一個簡單的含時外場 (如(1)式的哈密頓量),而是一個由如下非厄米哈密頓量描述的系統:

這就是非厄米線性響應公式[14].盡管從形式上與厄米版本的線性響應公式有所不同,但兩者的本質相同,即系統的響應都由系統的關聯函數決定.得到這一理論公式之后,下面將把它應用在不同的物理系統中.

3 非厄米線性響應理論在量子多體系統中的應用

本節介紹非厄米線性響應理論在量子多體系統中的應用,包括二維Bose-Hubbard 模型和一維相互作用量子氣體.

3.1 二維Bose-Hubbard 模型

2020 年,法國巴黎高師的冷原子實驗組測量了二維光晶格中Bose-Hubbard 模型在兩體耗散下的動量分布的耗散動力學演化,觀測到了非指數衰減和亞擴散現象.針對其實驗結果,本文從如下的哈密頓量出發:

此時可以發現動量的響應由系統的多點關聯函數決定.通常量子多體系統中的多點關聯函數是無法嚴格計算的,為此采用維克分解[20],將多點關聯函數分解為兩點關聯函數:

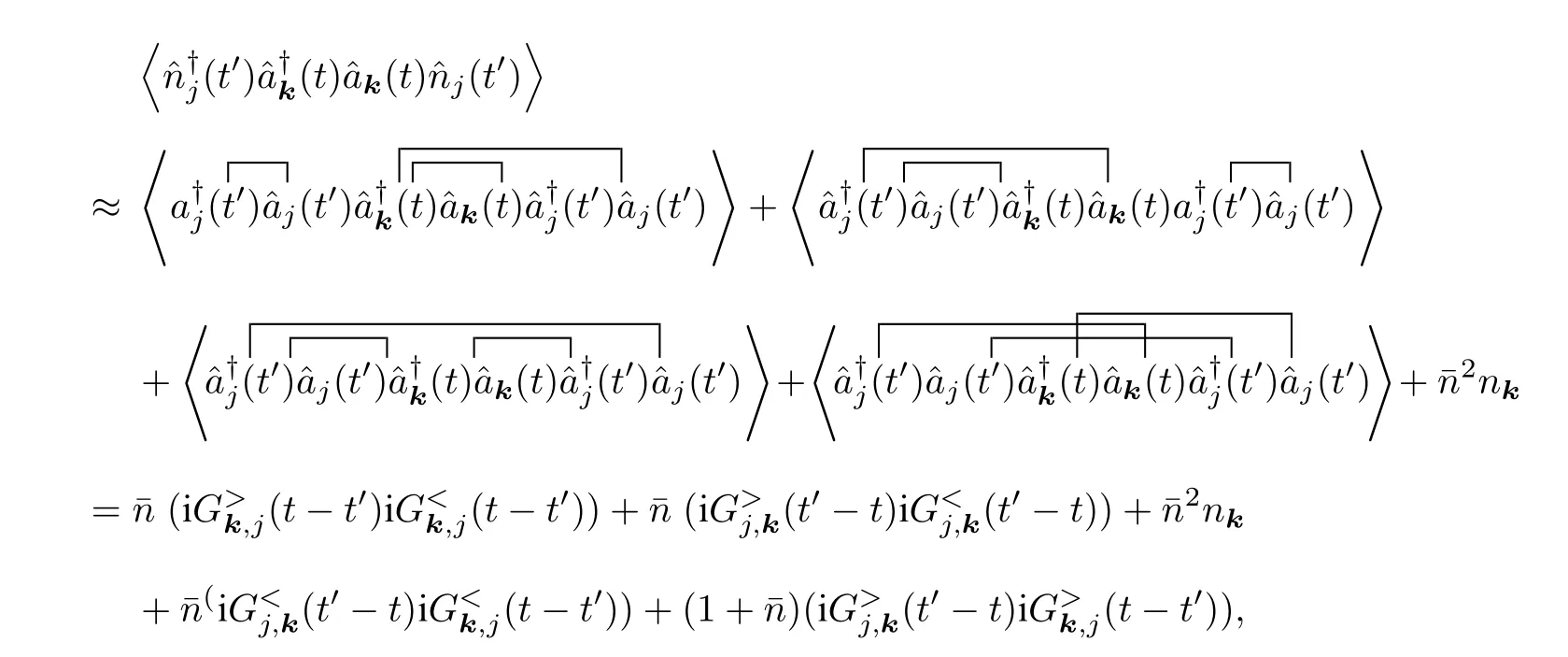
其中 1 /Γk代表準粒子的壽命.此時,

理論結果表明,對于處在準粒子激發的系統,其耗散動力學是指數衰減的,這就解釋了為什么指數衰減在自然界如此常見,因為自然界中的絕大多數量子物態可以被準粒子激發描述,如費米液體、玻色超流體等.而冷原子實驗已具備精確測量譜函數的技術條件[21],基于時間飛行(time-of-flight)測量和射頻譜(radiofrequency spectroscopy)技術[22—25],實驗可以精確測出動量和頻率依賴的譜函數Ak(ω) .以此可從譜學測量上為我們的理論預言提供實驗驗證.

當系統處于量子臨界相時[26],系統的激發不再是良好定義的準粒子激發,而是集體激發,譜函數的解析性質從極點變為割線[27]:

基于上面相同的分析,可以發現當系統處于超流相時,動量寬度在短時區域屬于正常的擴散行為:而在量子臨界區域,動量寬度的變化則出現反常的亞擴散行為:.我們即將看到,這一理論可為實驗結果提供一個統一的解釋.

如圖1(a)所示,我們發現理論曲線無論是動量高度還是動量分布的寬度都與實驗數據符合得很好,并且高度和寬度可以被同一個函數描述.

圖1 二維Bose-Hubbard 模型耗散動力學實驗[13]和理論對比圖 (a) 在固定光晶格勢阱深度下的動量分布的峰值和寬度隨時間的改變,實線是理論公式擬合的結果;(b) 在不同光晶格勢阱深度下的動量峰值隨時間的演化圖(以δnk=0(0)為單位).實線是理論公式擬合結果,插圖畫出了每條曲線對應不同的臨界指數 η,其中誤差棒來源于標準的擬合誤差(9 5% 的置信區間).兩個箭頭標注的分別是填充因子 ν =1 和 ν =2 的超流-Mott 絕緣體 轉變的 臨界值.所有的實驗數據(包括誤差棒)均取自實驗文章[13]Fig.1.Experimental data reported in Ref.[13] versus theory on dissipative two-dimensional Bose-Hubbard Model: (a) Two sets of data δ nk=0(t) and δ 〈k2〉(t) perfectly coincide with each other by a properly chosen scaling factor.Solid line is fitting with our theory.(b) Fit experimental data of δnk=0(t) (scaled by δ nk=0(0)) at different lattice depths with our theory,which yields η for different lattice depths shown in the inset where the error bar comes from the standard fitting error (9 5% confidence interval).Two arrows label the critical value for superfluid-Mott insulator transition for filling number ν =1 and ν =2,respectively.All experimental data are taken from Ref.[13].

不僅如此,在不同光晶格勢阱深度下的實驗數據可以估計出臨界指數η,如圖1(b)所示.值得指出的是,對于二維Bose-Hubbard 模型,理論上很難得到精確的η值[27],對于量子蒙特卡羅的計算也是一個挑戰[30].通過理論公式與實驗數據的對比擬合,我們發現隨著勢阱深度的增加,系統從超流區域到Mott 絕緣體轉變的過程中臨界區域η先減小后增大,這一結果解釋了實驗在弱勢阱區域觀測到的指數衰減和正常擴散行為,以及在深勢阱區域觀察到的非指數衰減和亞擴散現象.而且臨界指數η在超流-Mott絕緣體轉變的臨界區域達到最低值(約為3/4),此時系統動量分布以的形式衰減,同時動量寬度出現t1/4形式的亞擴散.這一結果也在實驗中得到了驗證.

因此,基于理論對實驗現象的詮釋,實驗出現的非指數衰減和反常的亞擴散行為起源于系統在量子臨界區域的集體激發.更重要的是,非厄米線性響應理論提供了一種通過耗散動力學在實驗上區分正常物態(準粒子激發)和量子臨界態(集體激發)的手段,利用實驗結果確定系統的臨界指數,對量子物態的實驗測量具有重要意義.

3.2 一維相互作用量子氣體

在3.1 節可以看到非厄米線性響應理論在耗散二維Bose-Hubbard 模型中的應用并很好地解釋了實驗結果.但一個成功的理論不僅能夠解釋已有的實驗,還應該具有預言能力.通過前面的討論可以發現,理論預言的反常動力學行為與系統的譜函數的奇異行為有關.因此,只要找到類似于(25)式的譜函數即可得到這種反常動力學.我們知道,一維相互作用系統中費米液體理論失效,其低能激發不再是準粒子激發,而是集體激發,此時譜函數具有類似(25)式的冪律形式[31].基于這一點,我們將非厄米系統應用于嚴格可解的一維相互作用量子氣體當中,精確地計算出臨界指數,以此來預言此類系統動量分布的耗散動力學演化.

以一維相互作用玻色氣體 (Lieb-Liniger 模型)為例[32],系統的哈密頓量為

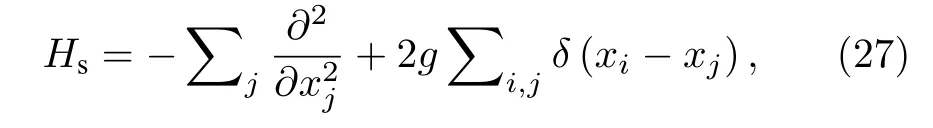
其中g為相互作用強度,這里令 ? =2m=1 .這一模型的低能物理可以被如下形式的有效哈密頓量描述:

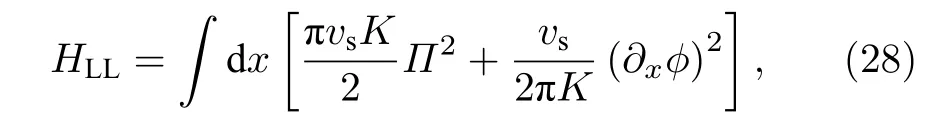
其中正則動量Π與相位?滿足標準的玻色對易關系;K和vs分別為Luttinger 參數和聲速,刻畫了系統低能和長波極限下的行為.根據Luttinger 液體理論,一維Bose 氣體的譜函數一般寫為如下形式[33]:

亦即η=1-1/(4K) .這意味著一旦求出Luttinger參數,就可以確定臨界指數的大小,而K的精確解可以通過Bethe ansatz 方法得到.寫出Lieb-Liniger玻色氣體的Bethe ansatz (BA)方程[34],

為方便起見,對系統的參數進行無量綱化:

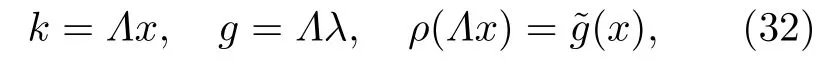
此時BA 方程重新表示為

由此可將得到的臨界指數η代入動量分布的響應公式(25),從而得到動量分布在整個相互作用范圍內的耗散動力學演化.在精確求解BA 方程之前,先來看系統在強弱相互作用極限的行為.在弱相互作用極限,無量綱能量可展開為

則Luttinger 參數和臨界指數的漸進行為是

而在強排斥相互作用極限(Tonks-Giradeau 極限)下

Luttinger 參數和臨界指數的漸進形式是

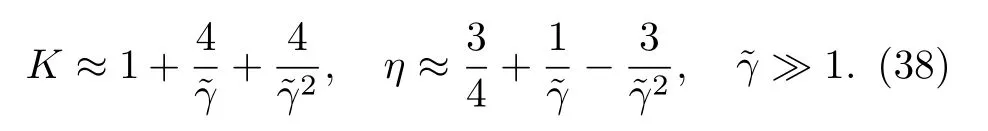
此時可以發現,在Tonks-Giradeau 極限下,系統在兩體耗散時的動量分布會以如下函數形式隨時間演化:

圖2 一維相互作用玻色氣體(Luttinger 液體)中的動量分布 δ nk(t) 從弱相互作用極限(藍線)到強相互作用極限(紅線)的含時演化的理論預測.這里所有的曲線均取τ0=1.0 ms .插圖表示的是臨界指數 η 隨相互作用強度的變化曲線Fig.2.Prediction of δ nk(t) for a one-dimensional Bose gas(Luttinger liquid) from the weakly interacting limit (blue line) to the Tonks limit (red line).Here τ 0=1.0 ms is fixed for all plots.The inset shows how η changes with the one-dimensional interaction parameter g /n .

圖2 給出了4 個不同相互作用強度下的動量演化曲線,可以看出隨著相互作用的增強,臨界指數η逐漸下降,使得動量分布的衰減逐漸減慢.由于實驗已經完成了關于Lieb-Linger 模型的臨界行為的精確測量[36],因此這一結果提供了清晰的理論預言并可以用當今的超冷原子實驗進行檢驗.

還可以將非厄米線性響應理論應用于一維費米氣體當中,對于無自旋或具有SU(2)對稱性的兩分量費米氣體,臨界指數[37],在強排斥極限下 (K=1/2 ),η=7/8,此時系統將會出現型的衰減和 Δk～t3/8形式的亞擴散,這種不同于玻色氣體的指數可以作為實驗驗證費米系統耗散動力學的證據.

到此,可以看到非厄米線性響應理論不僅成功地解釋了實驗,還提出了進一步的理論預言.讀者可以很容易想到,任何沒有準粒子激發的非正常量子物態都可以出現非指數的耗散動力學行為,如Luttinger 液體、非費米液體等.我們的非厄米線性響應理論最近受到一些理論研究者的關注,并被推廣到更一般的情況[38],同時也促使了關于非厄米Luttinger 液體等非厄米量子多體理論的研究[39—41].此外,這一響應理論還被用來研究黑洞的信息丟失佯謬[42,43].

4 時間反演對稱性保護的量子系統

對稱性是20 世紀物理學的主旋律之一,貫穿于現代物理學的各個領域.根據著名的Noether 定理,如果(經典)系統有連續的對稱性,則一定有相對應的守恒量①在量子力學層面上Noether 定理可能會失效,造成守恒被破壞的物理機制稱為“量子反常”(quantum abnormal)..對稱性在量子物理當中顯示出了巨大的威力,對稱性決定相互作用,對稱性自發破缺等觀念早已深入人心.在凝聚態物理中,對稱性在相和相變中扮演著重要角色.根據Landau 理論,物質的相可以用局域序參量來描述,而局域序參量從零(無序相)變到非零(有序相)則對應于系統的對稱性發生了自發破缺.因此,理論上可以用不同的對稱群來區分不同的物相.描述不同物相之間相變的Ginzburg-Landau 理論對相和相變的描述是普適的,只與系統的對稱性有關,而不依賴于其微觀的細節.這一點也顯示出了對稱性的巨大威力.

我們知道在量子力學中,如果一個系統具有某種對稱性,那么系統的能級往往會具有簡并.如我們熟知的氫原子中的旋轉對稱性導致的能級簡并,費米子系統中的時間反演對稱性導致的Kramers簡并等.如果對系統外加一個微擾,假如微擾也具有導致能級簡并的對稱性,那么能級仍是簡并的;假如微擾不具有這種對稱性(對稱性更低),那么相應的能級簡并也會被破除.這一基本的事實來源于Schur 引理[44]: 如果一個對稱操作的矩陣表示與某個幺正群的所有群元的不可約表示矩陣都對易,那么該矩陣一定正比于單位矩陣.

根據量子力學中的Wigner 定理,量子系統的對稱變換有兩類,一類是幺正對稱,另一類是反幺正對稱.對于反幺正對稱,也有相應的Schur 引理[45]:如果一個厄米矩陣與某個幺正群的所有群元的不可約表示矩陣都對易,那么該矩陣一定正比于單位矩陣.也就是說,對于反幺正對稱性導致的簡并(如時間反演對稱性導致的Kramers 簡并),如果能級簡并不被外加微擾破除的話,除了要求微擾具有該對稱性之外還需要微擾算符必須是厄米的.將會看到,反幺正對稱性與幺正對稱性的這一差別在物理上會產生巨大的不同(這一點最先由McGinley和Cooper 在文獻[46]中指出).

本節以量子自旋霍爾效應和相互作用拓撲態為例,將非厄米線性響應理論應用于具有時間反演對稱性(反幺正對稱性)的系統當中.

4.1 非厄米線性響應理論在量子自旋霍爾效應中的應用

在傳統的凝聚態物理中,物質的屬性主要由兩個理論所描述: 其一是能帶論和費米液體理論,其二是相和相變的對稱性破缺理論.在20 世紀80 年代之前,這兩個理論幾乎描述了所有的凝聚態物質.前文提到,物質的相及其分類可以由Ginzburg-Landau 理論描述.然而自80 年代起,伴隨著整數霍爾效應、分數量子霍爾效應、銅氧化物高溫超導現象的出現,人們陸續發現了一系列超出Landau 范式的量子物態,這些奇異的量子物態的出現并沒有伴隨著對稱性的自發破缺,不能通過局域序參量來刻畫.如整數量子霍爾效應中的量子化電導平臺由體態的拓撲數刻畫,當霍爾電導值從一個整數變到另一個整數時,系統并沒有發生對稱性破缺,而是伴隨著拓撲數的改變.而拓撲數的變化需要體態能隙的關閉,因而量子霍爾電導平臺具有魯棒性,不會被外界雜質、缺陷等因素所破壞.隨后,在1988 年,Haldane[47]提出了一個六角晶格模型 (Haldane 模型),在沒有外磁場的情況下也可以發生量子霍爾效應,即量子反常霍爾效應.與整數量子霍爾效應一樣,量子反常霍爾效應的出現同樣破壞了時間反演對稱性.而時間反演對稱性會導致重要的物理結果,在2005 年和2006 年,Kane 和Mele[48]以及Bernevig 和張首晟[49]進一步考慮自旋軌道耦合效應,獨立地提出了實現量子自旋霍爾效應的模型.量子自旋霍爾效應中量子化的電導受到時間反演對稱性的保護.理論研究表明,在沒有磁性雜質等破壞時間反演對稱性因素干擾的情況下,實驗可以在足夠純凈的樣品上觀測到自旋霍爾效應的量子化電導平臺.然而,事情遠沒有理論想象得那么簡單.圖3是實驗在HgTe 量子阱中測量到的自旋霍爾電導的結果[50],可以看出在線性標度下電導的測量值并未明顯地出現量子化的值 (G=2e/h2),盡管實驗樣品具有很高的純度和高遷移率.而我們知道,早在20 世紀80 年代實驗就能夠非常清晰地觀測到量子霍爾效應的量子化電導了,但是在半導體工藝發展二十多年之后,實驗并未觀測到量子自旋霍爾效應中的量子化電導(至少遠未達到量子霍爾效應的精度),這似乎造成了一個疑難,本節試圖從理論上來解釋這一疑難出現的物理原因.

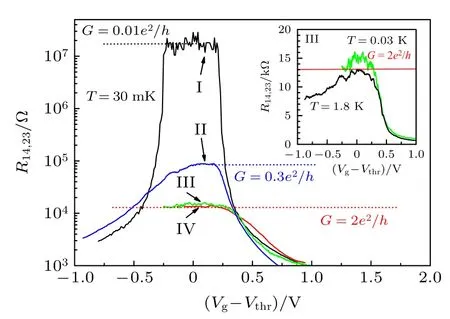
圖3 實驗測量縱向四端電阻隨門電壓變化曲線(對數坐標).插圖為線性坐標.圖片取自文獻[50]Fig.3.The longitudinal four-terminal resistance as a function of the gate voltage.The inset shows as a linear scale.The figure is copied from the Ref.[50].

首先,需要指出的是,與量子霍爾效應不同的是,量子自旋霍爾效應的拓撲態是受時間反演對稱保護的Kramers 簡并態,而時間反演對稱操作是反幺正的,這一點是理論解釋的關鍵.

下面以著名的Kane-Mele 模型為例來說明量子自旋霍爾效應的量子化電導為什么那么脆弱.Kane-Mele 模型是定義在二維蜂窩格子上的哈密頓量[48]:

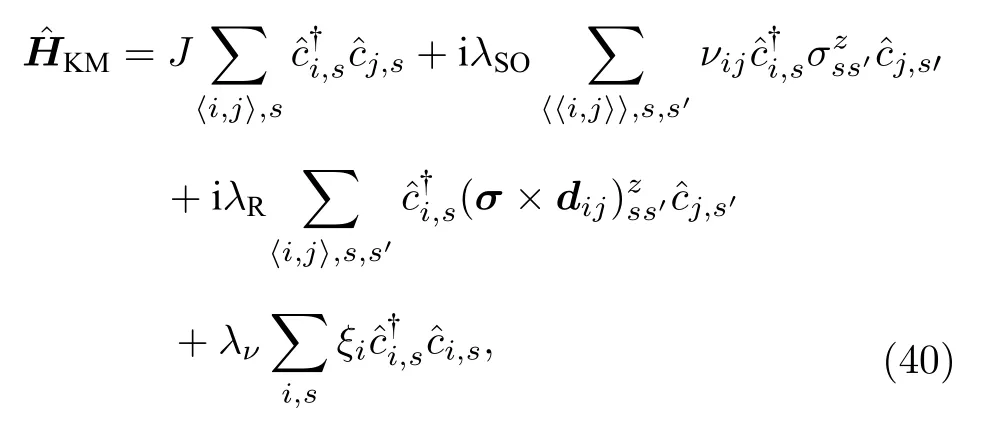
其中i,j是格點 指標;s,s′代表自旋指標;σ=(σx,σy,σz)表示Pauli 矩陣.哈密頓量中第一項是最近鄰的躍遷項(躍遷強度為J);第二項是次近鄰的自旋軌道耦合項(強度為λSO),其中νij=±1 ;第三項是最近鄰的Rashba 耦合項(強度為λR),其中dij是從i格點到j格點的空間矢量;最后一項是交錯勢(強度為λν,對于不同的子格ξi=±1).為了更清楚地研究需要論述的物理,我們將系統的參數區間選擇在非平庸的拓撲絕緣態中,并破壞掉鏡像對稱和反射對稱等幺正對稱性,使得能級的簡并性僅來源于時間反演對稱性.

然后,問一個基本的問題,由時間反演對稱保護的拓撲態 (或更一般的Kramers 簡并態)在外界耗散的影響下是否是穩定的? 容易想到,如果與外界環境自由度耦合的系統算符也具有時間反演對稱性,那么由時間反演對稱保護的拓撲態就應該不被破壞,除非耦合的算符本身不再具有時間反演對稱性.換句話說,只要在實驗上盡量排除掉破壞系統時間反演對稱性的因素(如外加磁場、磁性雜質等),那么實驗就能觀測到簡并拓撲態帶來的物理結果.

然而下面將會看到,這一基于對稱性分析的結論對于反幺正對稱性的情形并不成立.設系統受到外界環境的影響,按照前面的討論,其非厄米哈密頓量為

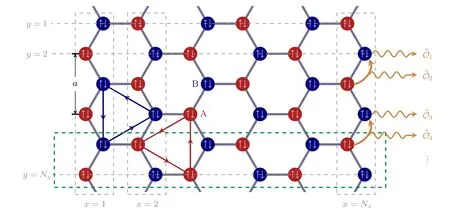
圖4 蜂窩格子上的Kane-Mele 模型,其中 x 方向取開邊界條件,y 方向上取周期邊界條件.系統尺寸為 N x×Ny .耗散耦合算符 位于右邊界,奇偶分別作用在連接和格點上Fig.4.Honeycomb lattice of the tight-binding Kane-Mele model with open boundary condition along x -axis and with periodical boundary condition along y -axis.The sample size is N x×Ny .The coupling operators are located on the right edge,which are defined on links for odd m and defined on sites for even m .

這里im代表邊界上的B 子格=m+1 .容易看出上述耗散算符是時間反演對稱的.有了以上這些定義就會看到,即使系統與外界環境耦合的是時間反演對稱的算符,時間反演對稱保護的簡并拓撲態也是不穩定的,以如下三個方面來論述這種不穩定性.

4.1.1 量子相干性的丟失

首先來看系統在時間反演對稱保護拓撲態的子空間(Kramers 空間)內的相干性.本文利用von Neumann 熵刻畫其子空間內相干性的變化.為此要計算系統約化密度矩陣的響應.在Schr?dinger繪景下,密度矩陣的含時演化為

4.1.2 簡并性的破壞

我們將看到,由時間反演對稱性導致的Kramers 態的簡并性也會被時間反演對稱的算符所破壞.定義推遲格林函數

4.1.3 背散射的出現

除了上述相干性的丟失和簡并性的破壞之外,我們還將看到,在破壞量子自旋霍爾效應的更重要的一個因素——背散射,也會因為耗散的存在而出現,即便耗散算符仍然是時間反演對稱的.

首先來看雜質勢在Kramers 簡并態之間的矩陣元

微擾展開并對Langevin 噪聲做平均后可得

這一結果也表明在量子霍爾效應中的拓撲邊緣態會被散射到另一個邊緣態,即出現背散射,導致自旋霍爾電導不再是量子化的.

系統在邊緣態中的有效哈密頓量可寫為

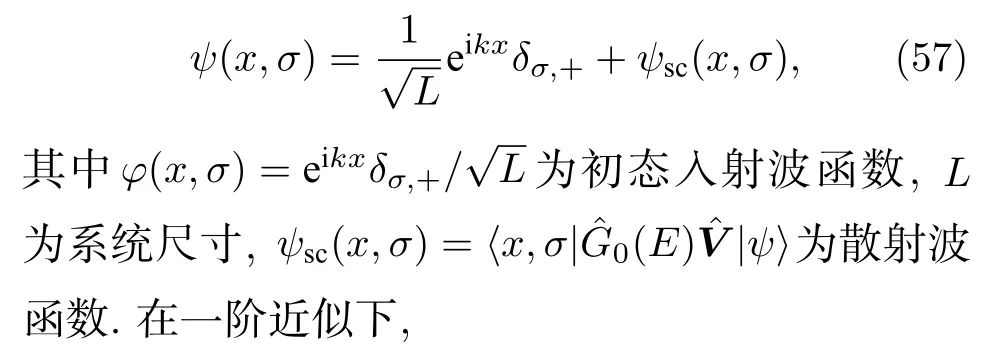
計算結果表明,在耗散的作用下,雜質確實會引起背散射(透射率不等于1),如圖5(c)中的插圖所示.不僅如此,反射率的大小也會隨著系統尺寸改變而變化,結果表明系統樣品的尺寸越大,反射率越高.這一結果與最近的實驗觀測到的結果[52]定性上是符合的,如實驗圖6 所示,電導隨著尺寸的增大逐漸偏離量子化的值,尺寸的閾值約為100 nm.對于非量子化的電導,之前有關的理論考慮了有限溫度下非彈性散射[53,54]以及電磁噪聲導致的散射帶來的影響[55].而我從理論上對于為什么實驗上很難觀測到精確的量子化電導[50,52,56,57]給出了另一種不同的物理詮釋,物理系統總是不可避免地受到外界環境的影響,對于時間反演對稱性保護的量子系統來說,即便與環境耦合的算符也具有時間反演對稱性,這種反幺正對稱性保護的物理也是不穩定的①即便系統被耦合的耗散算符是厄米算符,也不一定能保證這種穩定性.原因是可以利用兩個厄米算符構造出一個非厄米算符(在有限溫度下,γ1=γ2),同樣會導致Kramers 簡并態的不穩定性.只有一種極特殊的情況才能保持穩定,即系統只耦合一個算符且該算符是厄米算符..正是這種機制使得量子自旋霍爾效應中的背散射幾乎不可避免,導致電導量子化不再是精確的.

圖5 (a) von Neumann 熵隨時間的變化,三條曲線分別對應不 同耗散 耦合通 道數目: M =20 (實 線),M=16(虛線) 和 M =12 (點虛線);(b) Kramers 簡并空間中的譜函數;(c) 雜質勢的非對角元 V 12(t) 隨時間的變化,實線包含所有態的貢獻,虛線僅包含邊緣態的貢獻(M =20).插圖表示反射率隨樣品尺寸的變化.耗散強度 γ 大小為 0 .2J [51]Fig.5.(a) The von Neumann entropy S v(t) as a function of time.Here we choose the number of coupling operators as M =20 (solid line),M =16 (dashed line),and M =12(dotted dashed line),respectively.(b) The spectral function A (ω) for two Kramers degenerate states with dissipation,with M =20 .(c) Time evolution of the matrix element of the impurity potential V 12(t) between two degenerate edge states with.The solid line includes contributions from all states and the dashed line only includes contributions from edge states.The inset shows the transmission coefficient as a function of N y .The dissipation strengthγ is taken as 0 .2J [51].

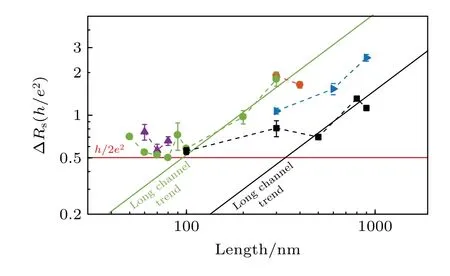
圖6 實驗在WTe2 樣品中測量的未摻雜通道電阻隨樣品尺寸的變化.圖片取自文獻[52]Fig.6.Length dependence of the undoped-channel resistance in WTe2 sample.The figure is copied from the Ref.[52].

4.2 非厄米線性響應理論在相互作用拓撲態中的應用

除了量子霍爾效應以外,我們利用非厄米線性響應理論來研究具有時間反演對稱性的相互作用拓撲相的穩定性問題.我們知道,根據Mermin-Wagner 定理[58],對于維數小于等于二維的系統,不存在有限溫度的長程序,即不會出現對稱性自發破缺.如一維反鐵磁Heisenberg 模型:

無論自旋取半奇數還是整數,系統的基態都沒有長程反鐵磁序.但是,Haldane[59,60]在1983 年發現,整數自旋的反鐵磁Heisenberg 模型的磁激發譜與半奇數有著巨大的區別,即半奇數自旋的激發譜是無能隙的,而整數自旋的激發譜卻是有能隙的(Haldane gap).從場論角度出發,Haldane 將反鐵磁自旋鏈的低能有效作用量寫為正常的O(3) 非線性σ-模型(O(3) nonlinearσ-model)部分S0[n] 與拓撲項Stop[n] (θ-term)部分之和:

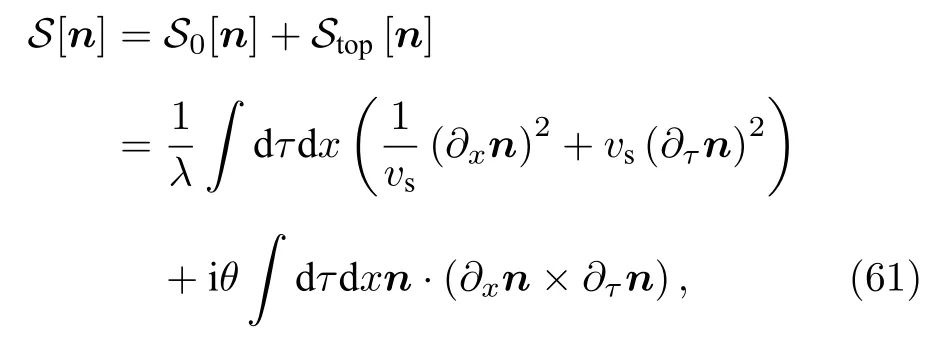
其中λ=4/S,θ=S/2 .vs表示長波極限下自旋波激發的波速.對于S0[n] 部分,在平均場近似下,體系的低能激發是無能隙的②在平均場近似下,n =? (? 為標量),此時于將 給出波動方程方程,所以此時系統的激發是無能隙的(ε (p)～vS|p|)..而量子漲落將改變體系的激發譜,使激發譜出現能隙.對于拓撲項,為了看出這一項的影響,我們將配分函數寫為如下求和形式:

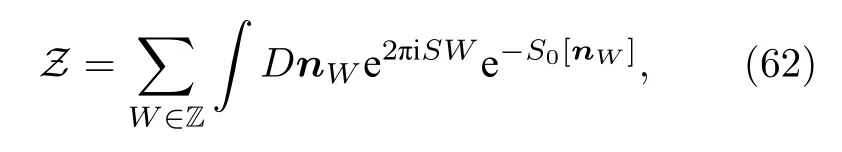
其中W表示纏繞數(winding number),nW代表纏繞數的場分布.顯然,拓撲項的貢獻只依賴于2S的奇偶性.對于整數自旋(2S為偶數),此時拓撲項的相位貢獻全都是 2π 整數倍,即 e xp(2πiSW)=1,這表明整數自旋的拓撲項對配分函數沒有貢獻(與沒有這一項的效果一樣),因此可以預期系統的能譜與于S0[n] 給 出的能譜一致.而對于半奇數自旋(2S為奇數),e xp(2πiSW)=(-1)W,即纏繞數W為奇數時會貢獻一個負號,這一正負號交替會讓相位在求和過程中相干相消,使得量子漲落對平均場的影響受到抑制,使系統的激發更接近平均場的無能隙激發.事實上,自旋 1 /2 反鐵磁Heisenberg 模型的Bethe ansatz 嚴格解給出的低能激發確實是無能隙的.因此Haldane 提出,所有整數自旋的反鐵磁Heisenberg 模型的激發譜都是無能隙的,而整數自旋是有能隙的,稱為Haldane conjecture.不僅如此,能隙是能夠穩定存在的,不受外界擾動或參數的變化(如將系統改為各向異性的XXZ 模型)而消失.這種有能隙且穩定存在的量子態構成一個非平庸的量子相(其基態沒有對稱破缺,但因為存在邊界態,而與平庸的有能隙的直積態有本質區別),被稱為Haldane gap.Haldane gap 后來在90 年代被密度矩陣重整化群的計算所驗證[61],中子散射實驗也觀察到了這一能隙[62].Haldane 的這一發現毫無疑問是重要的,也是令人驚奇的①這個結果令人驚奇的地方就在于,一方面,在大自旋極限下(S ?1),平均場的結果是越來越精確的,給出無能系線性色散;另一方面,對于 S =1/2,Bethe ansatz 的嚴格結果也給出無能隙的線性色散.那么自然應該期待對于中間大小的自旋 S ＞1/2,都應該具有無能隙的激發才對.但是,S =1 的系統卻是有能隙的！.它使人們意識到,在沒有對稱性自發破缺和長程序的系統中也可以有不同類別的物相,這里即是對稱性保護的拓撲物相(Haldane phase).而且,事實上自旋的整數和半奇數的區別是量子力學的效應,并沒有經典對應,這說明Haldane phase 完全是量子效應在相互作用多體系統中的體現.在Haldane conjecture 提出之后,1987 年由Affleck,Kennedy,Lieb 和Tasaki 四位物理學家提出了一個基態為Haldane phase 并且可以嚴格求解的模型(AKLT模型)[63],其哈密頓量為

圖7 AKLT 模型基 態示意 圖.其中每 個格點 上的自 旋S=1 (綠色橢圓)被分解成兩個自旋 S =1/2 (藍色圓點),被黑色直線連接起來的兩個藍點表示兩個自旋 S =1/2 形成的自旋單態.左右邊界上的紅色圓點表示自由的自旋S=1/2Fig.7.A schematic diagram for groundstate of the AKLT model.The spin S =1 (green oval shape) at each site is split into two spin-half (blue dots),and two blue dots connected by black line represents the spin singlet formed by the two spin S =1/2 .The red dot at each boundary represents free spin-half.

將每個格點的自旋S=1 (圖7 中的黃色圓圈)分解為兩個自旋 1 /2 組成的自旋三重態,則基態可視為臨近兩格點接觸的自旋 1 /2 形成的自旋單態,此時兩個邊界格點各有一個未配對的自由的1/2自旋態,所以基態是四重簡并的零能態.換句話說,系統的基態在體內是自旋單態構成的直積態,而左右邊界上則各存有一個S=1/2 的邊界態.系統的激發是有能隙的,激發態需要打破自旋單態,導致正比于J的有限 能量增 加.與Haldane phase 一樣,AKLT 模型的基態是拓撲非平庸的②其基態沒有對稱自發破缺,但是存在邊界態,這與平庸的有能隙的直積態本質上是不同的.,它受時間反演對稱和二面體群D2(關于兩個正交軸的 π 旋轉)的保護[64].

本節的目的就是以AKLT 模型為例,通過退相干的出現和簡并性的破壞,來表明受時間反演保護的Haldane phase 在耗散下的不穩定性.為此,先將其基態重新表示.

根據自旋算符的Schwinger 玻色子表示,

為了討論這類對稱性保護的基態在耗散影響下的穩定性,從譜的簡并性和基態空間的相干性兩方面來討論.定義格林函數:

事實上,通過Kane-Mele 模型和ALKT 模型的計算過程可以發現,耗散引起時間反演對稱保護的量子系統的不穩定性是普適的,并不依賴于具體的模型,其背后的數學原因是反幺正群的Schur 引理.“光陰似箭,歲月如梭”,自人類文明起始以來,時間可能是最神秘的概念.我們知道,宏觀熱力學系統的時間箭頭起源于微觀概率的最概然分布,體現在熱力學熵的增加,但是在微觀上,熱力學系統中的單個原子的運動總是可逆的.然而具有時間反演對稱的量子系統中的時間箭頭,則是起源于時間反演對稱的反幺正性,這里的不可逆性體現在Kramers 簡并空間中von Neumann 熵的增加.從物理上看,這似乎提供了一種“時間箭頭”的可能的微觀起源,即自然界的時間流逝總是單向的原因,就是時間反演對稱性是反幺正的.

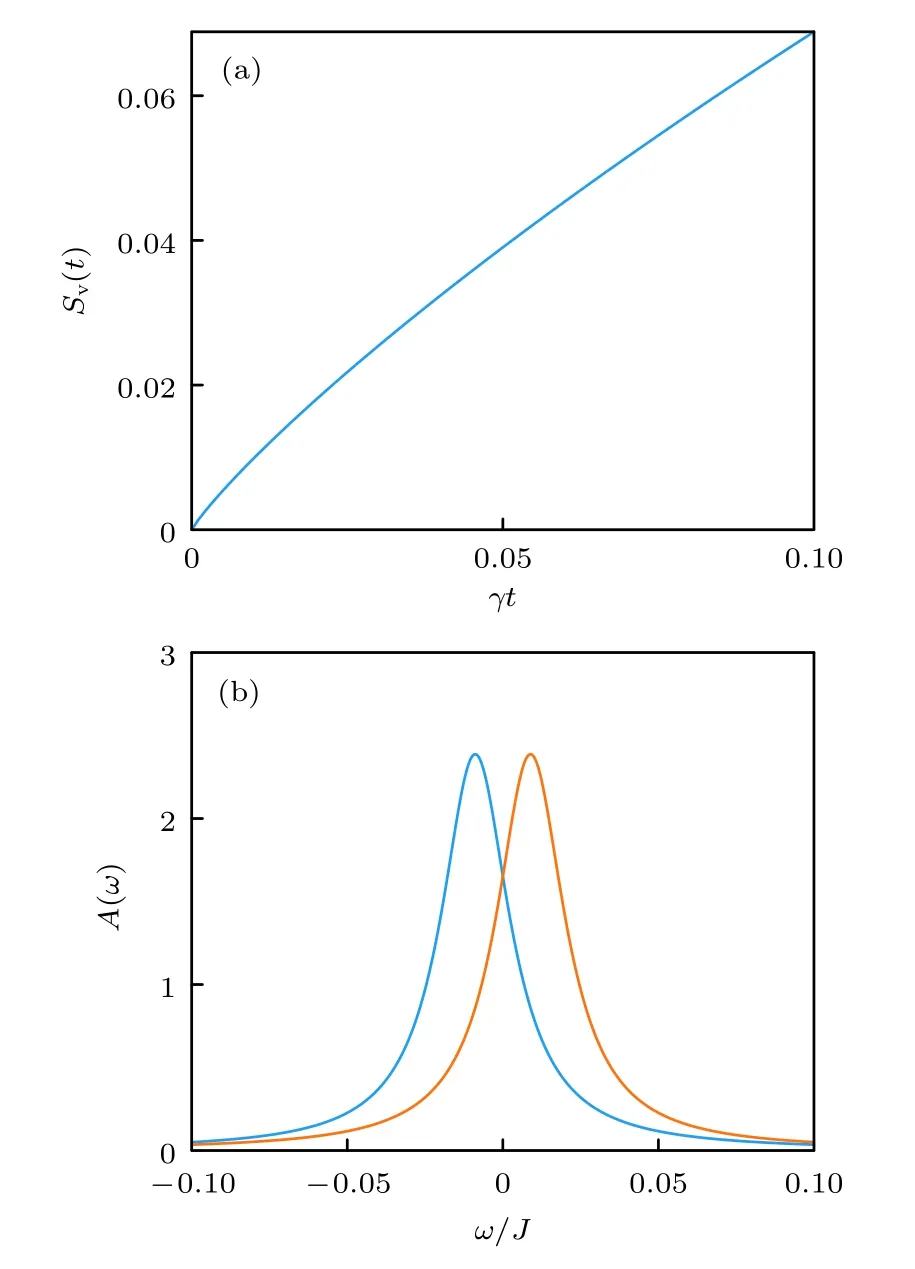
圖8 (a) AKLT 模型中的von Neumann 熵隨時間的變化;(b) 基態空間中的譜函數Fig.8.(a) The von Neumann entropy as a function of time in the AKLT model;(b) the spectral function in groundstate subspace.

5 總結與展望

本文簡要地綜述了非厄米線性響應理論以及該理論在具有耗散量子多體和具有時間反演對稱保護的量子系統這兩大方面的應用.在耗散量子多體系統方面,發現在二維Bose-Hubbard 模型中,當系統處于具有良好定義的準粒子激發狀態時,系統的耗散動力學出現正常的指數衰減和擴散行為;而當系統處于量子臨界狀態時,則會出現非指數衰減的耗散動力學和反常的亞擴散行為,并且這些反常行為與系統在臨界相的臨界指數決定.理論計算的結果與冷原子實驗觀測數據高度符合.另外還發現,在一維量子氣體中,系統處于Luttinger 液體態時也會出現類似的非指數和亞擴散行為.這一理論的結果提供了一種通過實驗測量耗散動力學來區分正常量子物態和臨界量子物態的手段,也為實驗測量臨界指數提供了新的方法.在時間反演對稱的量子系統方面,以量子霍爾效應和相互作用拓撲態為例,通過非厄米線性響應的計算,發現了由時間反演這種反幺正對稱性保護的Kramers 簡并及其相關的物理性質在耗散的影響下并不是穩定的,即便耗散算符也同樣具有時間反演對稱性.理論預言了自旋霍爾電導不再是精確的量子化值,且隨實驗樣品尺寸的變化規律與實驗結果定性一致.從以上兩方面的應用來看,非厄米線性響應理論是成功的.誠然,正如前言所講,非平衡動力學過程原則上涉及系統所有的自由度,理論上來說很難通過少數幾個參數就能精確刻畫多體系統動力學演化.非厄米線性響應理論處理是系統在耗散影響下的準靜態演化過程,當系統的演化狀態非準靜態過程的時候,還沒有理論可以有效地處理.一個具有重要意義的問題是,非平衡動力學是否有類似于平衡態物理一樣的普適性(如量子相變的普適類)? 有趣的是,實驗在遠離準靜態的非平衡動力學中發現了一些普適的動力學行為,驗證了這種存在的可能性.如遠離平衡態的普適淬火動力學[67],以及最近在量子多體系統中觀測到的著名的Kardar-Parisi-Zhang 普適性[68—70].“平衡態系統都是相似的,而非平衡系統卻各有各的非平衡”.我們相信,自然界中的精彩很大程度上來自于非平衡物理.伴隨著實驗技術尤其是冷原子實驗的蓬勃發展,我們有理由期待,非平衡物理系統會帶給我們越來越多的驚奇.

本文所介紹的非厄米線性響應理論是作者與多位合作者共同提出的.借此機會,作者要感謝清華大學高等研究院的翟薈教授,正是翟薈教授對物理理論的獨到見解以及對實驗現象的真知灼見,非厄米線性響應理論才得以誕生.感謝中國工程物理研究院的陳宇研究員,陳教授扎實深厚的物理功底和他那爽朗的笑聲,為本工作的進展過程增輝不少.感謝清華大學高等研究院的陳鑫博士和鄧天舒博士,和他們的討論亦使作者受益良多.作者還要感謝中國科學院物理研究所的陳澍研究員和崔曉玲研究員,在他們的指引下作者有幸進入了量子開放系統和非厄米物理這一蓬勃發展的領域.