疇壁系統中的非厄米趨膚效應

鄧天舒

(清華大學高等研究院,北京 100084)

非厄米趨膚效應是近幾年非厄米物理研究領域中的熱點問題,它揭示了非厄米系統中體態波函數和能譜計算會敏感依賴于邊界條件的新奇現象.人們提出廣義布里淵區的概念用以刻畫非厄米系統中的體態波函數和能帶性質.基于廣義布里淵區計算的非布洛赫拓撲數可以重新構建非厄米拓撲體邊對應關系.然而,過去關于非厄米趨膚效應的討論主要針對開放邊界條件,如果采用疇壁邊界條件,廣義布里淵區和非布洛赫拓撲數的計算都需要重新考慮.本文綜述了近幾年關于疇壁邊界條件下非厄米趨膚效應的若干研究工作,首先從一般的一維非厄米單帶模型出發,推導廣義布里淵區方程的一般形式;然后回顧了非厄米SSH (Su-Schieffer-Heeger)模型中廣義布里淵區和非布洛赫拓撲數的計算;最后在一維光量子行走的系統中,介紹了實驗上非厄米趨膚效應的實現和非厄米拓撲邊緣態的探測.

1 引言

在孤立的量子系統中利用厄米型的哈密頓量來研究物相的基本性質是量子物理研究的基本范式.然而實際上,絕對孤立的系統是不存在的,因此人們發展了一系列理論用于描述與環境有相互作用的系統的演化,其中一個最為經典的描述就是在馬爾科夫近似下得到的Lindblad 量子主方程[1,2].量子主方程的研究常常需要涉及到非厄米的哈密頓量: 一方面,在忽略量子躍遷效應時,Lindblad型主方程可以直接近似為非厄米哈密頓量下的薛定諤方程[3,4];另一方面,如果把密度矩陣映射為雙希爾伯特空間的波函數,那么其在主方程下的演化可以嚴格映射為雙空間波函數在非厄米哈密頓量下的演化[5—7].相較于量子主方程,非厄米哈密頓量的描述在形式上顯得更為簡潔,將之與傳統厄米哈密頓量中的各種經典理論結合,就有可能建立新的理論框架,做出新的理論預言.如非厄米拓撲能帶理論的發展就是將非厄米哈密頓量與傳統拓撲能帶結合的典型范例[8—12].此外,近年來隨著實驗技術的發展,人們有能力在越來越多的物理系統中模擬非厄米哈密頓量[13—19],這進一步促使人們探索非厄米系統中的種種新奇現象.其中廣受關注的一個成果就是關于非厄米趨膚效應的研究[20—25].

非厄米趨膚效應指的是在非厄米系統中,體態波函數局域在邊界附近的現象.為了刻畫這種效應,需要將傳統的布洛赫能帶理論修正為非布洛赫能帶理論.以一維系統為例,在傳統的布洛赫能帶理論中,無論是開邊界條件還是周期邊界條件,體態波函數都滿足布洛赫波的形式ψ(x)=eikx.然而在非厄米系統中,周期邊界條件下的體態波函數依然是布洛赫波;但是對于存在邊界的系統,波函數有可能會局域在邊界附近,其體態波函數會滿足ψ(x)=βx的形式,其中β=reik,r和k都是實數.這里的β會在復平面內形成一條封閉曲線,被稱為廣義布里淵區.在不同的系統中,不同邊界條件下求解這條封閉曲線的方程被稱為廣義布里淵區方程.基于廣義布里淵區可以正確地計算不同邊界下的實空間連續譜,即非布洛赫能帶.非布洛赫能帶理論最初的一個成功應用就是在非厄米拓撲問題中.在廣義布里淵區上做積分得到的非布洛赫拓撲數,可以正確地預測系統中拓撲邊緣態的產生與消失,而布洛赫拓撲數做不到這一點[21].這一案例表明,廣義布里淵區和非布洛赫能帶理論對理解和描述非厄米系統有著重要的意義.

非厄米趨膚效應被提出以來就吸引了凝聚態理論各界的廣泛關注,非布洛赫能帶理論取得了蓬勃發展,出現了很多重要成果[26—43],如開邊界條件下一維系統中廣義布里淵區方程的一般形式[26]量子主方程中的非厄米趨膚效應[32,34,37,38]、非厄米趨膚效應的拓撲起源[29,30]等.以上絕大多數的討論都是針對開邊界條件,而廣義布里淵區方程對邊界條件的依賴非常敏感,所以此時研究多種不同邊界條件下的廣義布里淵區是十分重要且必要的.本文重點關注疇壁邊界條件下的非厄米趨膚效應[17,44].疇壁邊界條件指的是把兩塊不同參數的材料拼接在一起形成的一種空間結構,在拓撲能帶理論研究中有著廣泛的應用[45—47].一方面,在該系統中研究廣義布里淵區可以幫助構建疇壁邊界條件下的非厄米體邊對應關系;另一方面,在很多量子模擬的實驗系統中,疇壁邊界條件比開邊界條件更容易實現(如光量子行走系統),因此對疇壁邊界條件下非厄米系統的深入研究也為實驗實現非厄米趨膚效應提供了更多的可能.

本文分為以下幾個部分對疇壁邊界條件下非厄米趨膚效應的相關研究展開綜述: 第2 節介紹在一般的一維單帶緊束縛模型中,廣義布里淵區方程的推導;第3 節以非厄米SSH (Su-Schieffer-Heeger)模型為例,介紹疇壁邊界條件下非布洛赫能帶理論的應用,以及非厄米拓撲體邊對應關系的構建;第4 節探討非厄米趨膚效應在一維量子行走體系中的實現方案,并再次應用非布洛赫能帶理構建非厄米拓撲體邊對應關系,最后討論實驗上對拓撲邊緣態的探測.

2 疇壁邊界條件下廣義布里淵區的計算

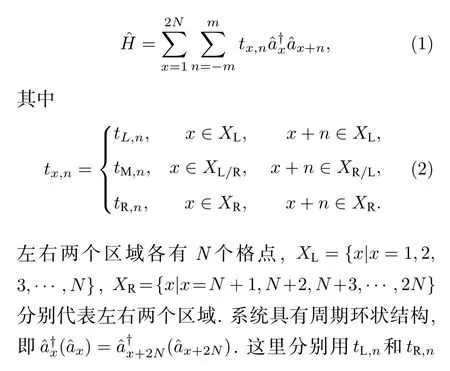
本節從一維單帶模型出發,推導疇壁邊界條件下的廣義布里淵區方程.考慮由兩個區域組成的一維單帶模型,兩個區域在邊界拼接到一起,形成疇壁邊界條件.如圖1 所示,其哈密頓量可寫作代表左右兩個區域內部相差n個格點的躍遷,m代表最大躍遷幅度.而tM,n代表所有跨越邊界的躍遷.圖2 給出了該模型中哈密頓量的所有本征波函數分布圖,可以看到,當,哈密頓量是非厄米的,波函數局域在了兩個疇壁附近,即非厄米趨膚效應.在遠離邊界的左邊(右邊)區域內部,系統具有平移對稱性,實空間波函數可分別表示為這里的βx可視作厄米哈密頓量中布洛赫波形式 eikx的推廣.對于給定的能量E,通過分析實空間的薛定諤方程可以得到特征方程hα(βα)=E,其中

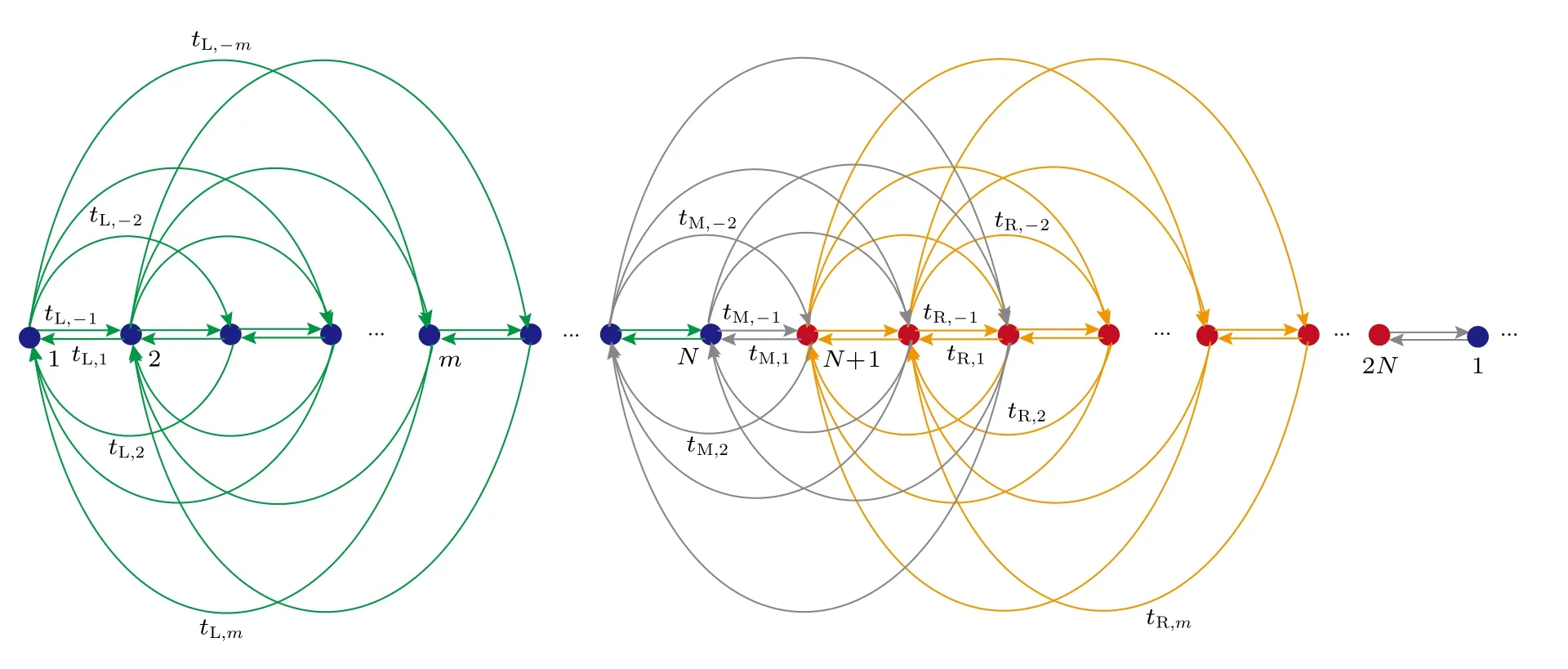
圖1 疇壁邊界條件下的一維單帶模型示意圖,格點首尾相連形成環狀結構.躍遷距離最遠為mFig.1.Illustration of single-band lattice model under domain-wall configuration.The hopping distance is m at most.

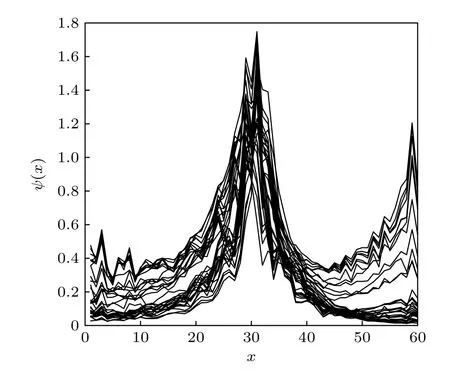
圖2 波函數在實空間的分布圖.其中 m =2,tM,1=tM,2=tM,-1=tM,-2=1,t L,-2=4,t L,-1=-1,t L,1=3,tL,2=2,t R,-2=2,t R,-1=1,t R,1=3,t R,2=-2,N=30Fig.2.Wave-function distribution in real space.Here,m=2,t M,1=tM,2=tM,-1=tM,-2=1,t L,-2=4,tL,-1=-1,t L,1=3,t L,2=2,t R,-2=2,t R,-1=1,tR,1=3,t R,2=-2,N =30 .

其中,Cn(Dn)是通解中的待定系數.需要注意的是此時得到的通解形式只考慮了哈密頓量左右區域內部的躍遷tL,n和tR,n,而沒有考慮跨越邊界的躍遷tM,n.這是因為tM,n作用在了邊界附近的 4m個格點,只有當討論邊界條件時才會引入tM,n的影響.

接下來把通解波函數代入到疇壁邊界條件下的哈密頓量中,得到 4m個邊界方程:

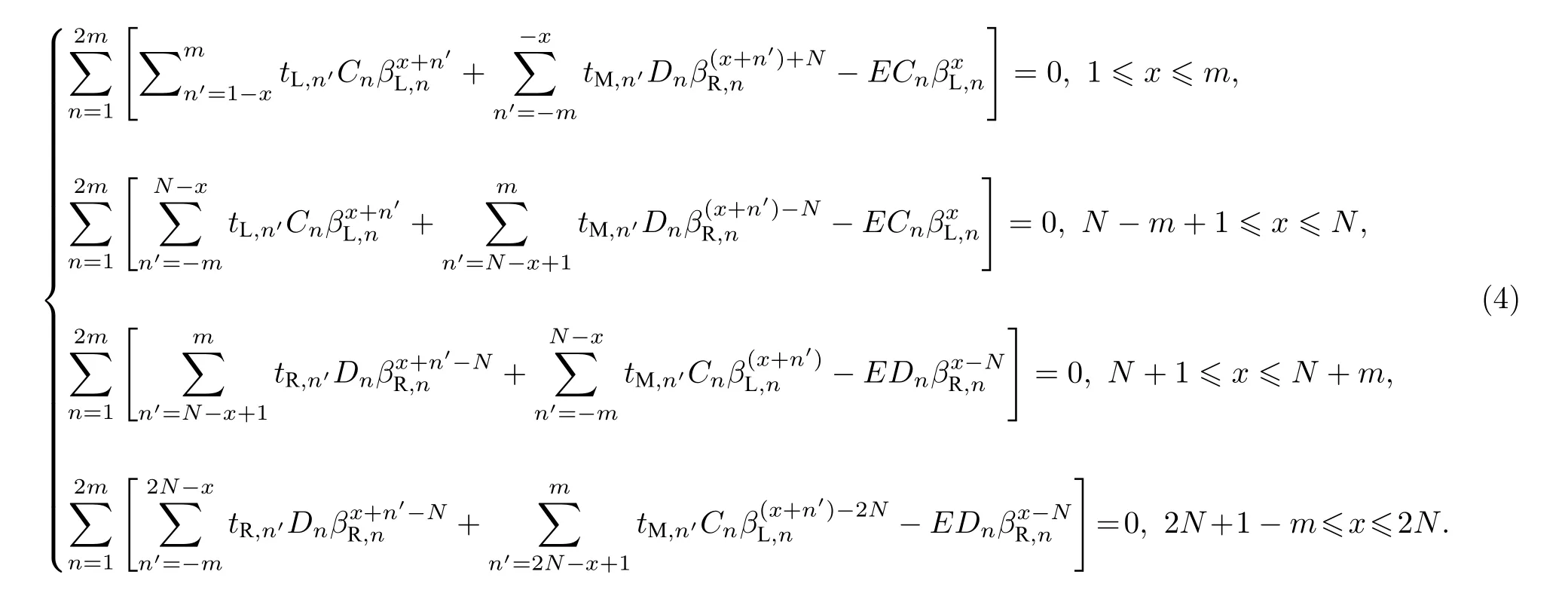
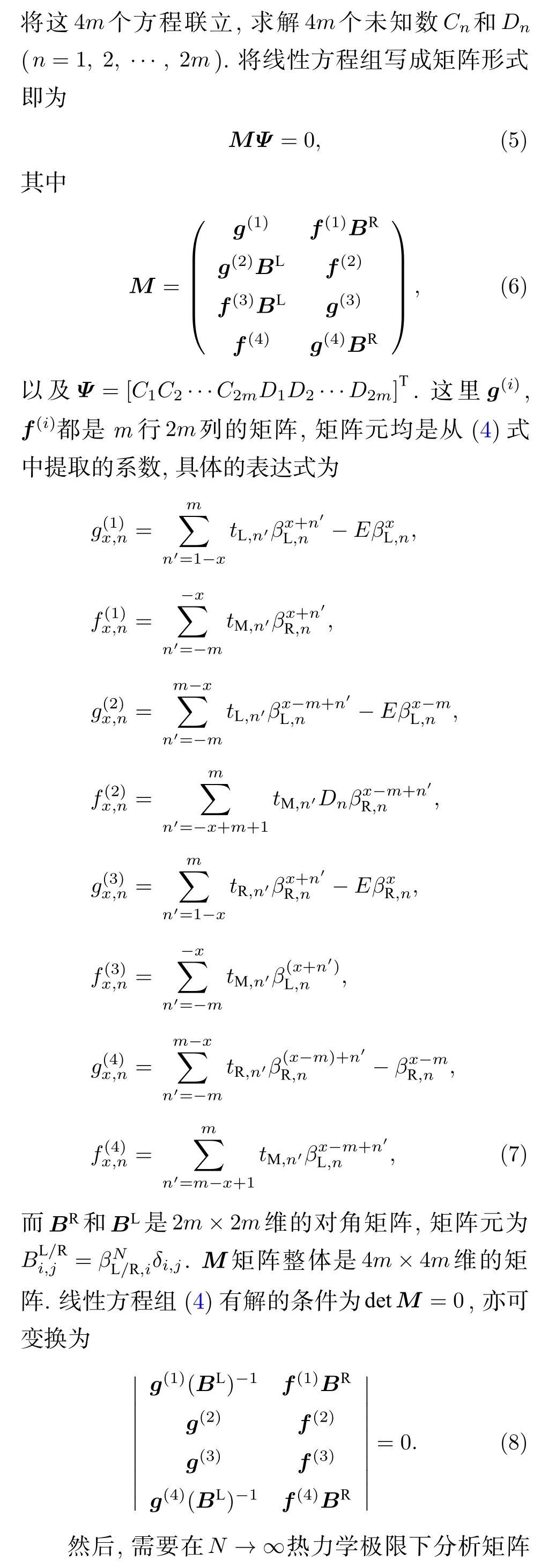
這里n=1,2,3,···,N,因此(12)式在熱力學極限下可求得無窮多個解[21].綜上,|η2m|=|η2m+1|即為廣義布里淵區方程,據此可以求出疇壁邊界條件下的廣義布里淵區和非布洛赫能帶的能量.值得注意的一點是,廣義布里淵區的計算與tM,n參數的具體取值無關.這體現出廣義布里淵區方程具有抗干擾性,只要兩塊材料在邊界上相連,相連處躍遷參數的擾動并不會影響兩塊體材內部廣義布里淵區的計算結果.

3 非厄米SSH 模型

本節將回顧疇壁邊界條件下的非厄米SSH 模型[44].以此模型為例,具體闡釋廣義布里淵區的計算,并將之應用到非厄米能帶理論中,計算非布洛赫能量和非布洛赫拓撲數,驗證疇壁邊界條件下非厄米系統中的體邊對應關系.

3.1 模 型

如圖3 所示,考慮疇壁邊界條件下的非厄米SSH 模型.開邊界條件下的非厄米SSH 模型過去有過許多討論[48,49],而在文獻[21]中首次利用廣義布里淵區概念解釋了該模型中反常的體邊對應現象.而疇壁邊界條件下非厄米SSH 模型的哈密頓量可寫作

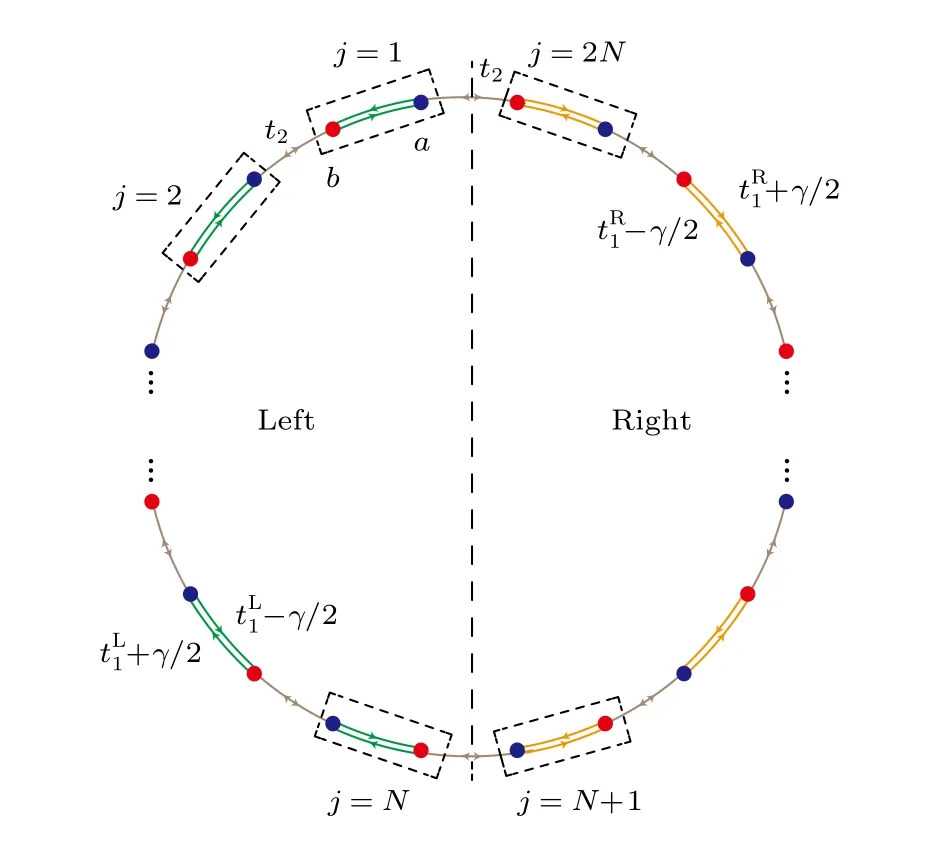
圖3 疇壁邊 界條件 下的非厄米SSH 模 型.在左邊(右邊)區域元胞內部a 子格到b 子格的躍遷是-γ/2,而元胞內部b 子格到a 子格的是 t L1(R)+γ/2 .此外,疇壁兩邊不同區域具有相同的 t2 和 γ [44]Fig.3.A non-Hermitian SSH model with two bulks.For left(right) bulk,the intra-cell hopping from a-site to b-site is-γ/2while the intra-cell hopping from b-site to asite is +γ/2 .Also,different bulks holds same t2 and γ[44].

該模型具有手征對稱性σzh(k)σz=-h(k) 和非厄米趨膚效應,是一個探討非厄米趨膚效應和非厄米拓撲能帶理論的經典模型.開邊界條件下的非厄米SSH 模型已經有過詳細的討論[21],在本節后面的部分,將集中討論疇壁邊界條件下非厄米SSH 模型中廣義布里淵區的計算方法,并基于此構建非厄米拓撲體邊對應關系.

3.2 廣義布里淵區

本節采用第2 節中的方法,具體探討廣義布里淵區的計算.首先可以將實空間哈密頓量中特定能量的本征態寫作

(18)式可化作一個關于β的一元二次方程,方程有兩個根,所以(16)式中的nmax取 2 .

將(15)式,(19)式和(20)式代入邊界條件:

由第2 節中相似的邏輯便可判斷,體態的波函數解的數目一定正比于N,為了滿足這一點,集合{ηi|i=1,2,3,4}中的元素一定滿足

這就是疇壁邊界條件下非厄米SSH 模型的廣義布里淵區方程.(29)式與文獻[44]中所給的廣義布里淵區方程完全一致,是一個更為簡潔的形式.

接下來詳細闡述如何由廣義布里淵區方程計算得到廣義布里淵區和非布洛赫能帶.形式上,(29)式是關于4 個變量βL,1,βL,2,βR,1,βR,2的方程.但是從(18)式可以看到,所有的ηi都由能量E決定,所以方程(29)中只有一個獨立的復變量(在非厄米系統中E和β一般都是復數).因此在方程(29) 的約束下,便可確定任意一個βα,n在復平面內形成的封閉曲線.具體來講,可以從βL,1=reip出發,先將完整的復變量βL,1=reip形式代入(18)式中,計算能量E,再通過能量計算βL,2,βR,1,βR,2.然后把求得的所有{1/βL,1,1/βL,2,βR,1,βR,2}進行排序,代入方程(29)中.于是方程(29)將變成一個關于r和p方程,遍歷p∈[0,2π),便可得到r關于p的函數,由此便可繪制左邊區域的廣義布里淵區的其中一支解.依照此法可求得所有的βα,n.

圖4(c)和圖4(d)分別給出了左邊區域和右邊區域的廣義布里淵區.在開邊界條件下的非厄米SSH 模型中,廣義布里淵區的方程寫作|β1|=|β2|,因此β的兩支解會在復平面內重合.僅將邊界條件改為疇壁邊界條件后,就會得到完全不同的廣義布里淵區,這也印證了非厄米趨膚效應對邊界條件變化的敏感性.

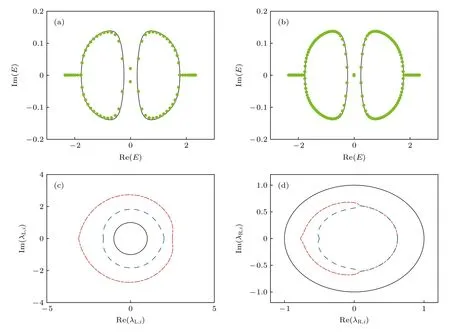
圖4 (a),(b)體態波函數的理論(黑線)和數值(綠點)結果,(a)圖的鏈長為 N =20,(b) 圖的鏈長為 N =40 .(c) 復平面內βL,1(紅色點劃線)和 β L,2 (藍色虛線)表示的左鏈的非布洛赫布里淵區.(d) 復平面內 β R,1 (紅色點劃線)和 β R,2 (藍色虛線)表示的右鏈的非布洛赫布里淵區.在圖(c)和圖(d)中,取熱力學極限 N →∞ 并且用黑色實線畫出了布洛赫布里淵區作為對比.在所有的子圖中,選取的參數為=-t2,=1.5t2,γ =1.33t2 [44]Fig.4.(a),(b) Theoretical (black lines) and numerical (green dots) results of bulk-state energy spectrum.The length of chain is N=20 for panel (a) and N =40 for panel (b).(c) Non-Bloch Brillouin zones of the left bulk,represented by β L,1 (red dash-dotted line) and β L,2 (blue dashed line) on the complex plane.(d) Non-Bloch Brillouin zones of the right bulk,represented byβR,1(red dash-dotted line) and β R,2 (blue dashed line) on the complex plane.In panels (c) and (d),we take the thermodynamic limit N →∞,and we also plot the Bloch Brillouin zones with black solid lines for comparison.For all subplots,we take =-t2,=1.5t2,γ =1.33t2 [44].

我們又將廣義布里淵區與布里淵區 eik在復平面上形成的單位圓做對比.需要注意的是,在兩種情況下,廣義布里淵區會退化為單位圓.一種情況是當哈密頓量為厄米的γ=0,另一種情況是系統具有周期邊界條件=.這表明非厄米趨膚效應是系統非厄米性與邊界條件共同作用的結果.

此外,本文還基于廣義布里淵區和特征方程,繪制了非布洛赫能帶(見圖4(a)和圖4(b)),并將之與實空間嚴格對角化哈密頓量的能譜作對比.可以看到在N=20 和N=40 的情況下,數值計算的能譜和廣義布里淵區的理論得到的非布洛赫能帶符合得很好,并且隨著N的增大,兩者的差距變得更小.這充分說明本文計算得到的廣義布里淵區在疇壁邊界條件下可以精確刻畫熱力學極限下實空間的本征能譜.

3.3 非布洛赫拓撲數與拓撲體邊對應關系

本節基于3.2 節得到的廣義布里淵區,計算疇壁邊界條件下的非布洛赫拓撲不變量,構建非厄米系統中的拓撲體邊對應關系.由系統的布洛赫哈密頓量(14)可知,系統具有手征對稱性,其拓撲不變量可以由Zak 相定義:

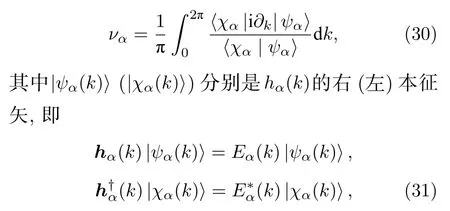
這里νL和νR分別代表左邊區域和右邊區域的拓撲數,兩者之差如果非0,疇壁上就會出現邊緣態,這就是傳統意義上疇壁邊界條件下的體邊對應關系.但是對于非厄米系統來說,需采用非布洛赫能帶理論,將積分區間從布里淵區修正為廣義布里淵區.因此將β=r(p)eip和h(β) 代入(30)式便可得到非布洛赫拓撲數的計算公式:

需要注意的是,從圖4(c)和圖4(d)可以看出,廣義布里淵區方程一般會求得r(p) 的兩支解,也就是說(32)式中有兩個可以選擇的積分區間分別對應βα,1和βα,2在復平面上形成的封閉曲線.在非厄米SSH 模型中可以證明,同一個參數下求得的兩個廣義布里淵區上積分得到的非布洛赫拓撲數是一致的[44].

圖5(d)—(f)分別把布洛赫和非布洛赫拓撲數和數值計算的能譜做對比,確認了非布洛赫體邊對應性.在厄米的情況下γ=0,非布洛赫和布洛赫拓撲數的結果一致,即當時系統存在零模.隨著γ增加,布洛赫和非布洛赫拓撲數之間的區別便顯現出來,左右區域非布洛赫拓撲數的差值可以正確地預測邊緣零模的出現與消失,而布洛赫拓撲數無法做到這一點.這進一步說明,相比于布洛赫拓撲數,基于廣義布里淵區的非布洛赫拓撲數更能正確地判斷系統拓撲性質的變化.

圖5 (a)—(c)顏色欄在 - 平面能譜絕對值的最小值.這里選取 N =40 .圖(a)中 γ =0,圖(b)中 γ =0.67 t2,圖(c)中γ=1.33 t2 .黑色線對應參數=,此時疇壁構型會退化回周期邊界條件的均勻格點模型.玫紅色的虛線對應的參數為=-.圖(a)—(c)里的紅色點劃線給出了用在圖(d)—(f)里的參數,即=1.5 t2 .(d)—(f)能譜絕對值(上部)和拓撲數(下部).圖中下部給出了左鏈的布洛赫拓撲數 νL (玫紅虛線) 和右鏈的非布洛赫拓撲數 ν R (黑色虛線),以及左鏈的非布洛赫拓撲數 (紅色實線)和右鏈的非布洛赫拓撲數 (藍色實線)[44]Fig.5.(a)—(c) Contour plots of absolute values of the energy-spectrum minimum on the -plane.Here,we take N =40 .We also take γ =0 for (a),γ =0.67 t2 for (b) and γ =1.33 t2 for (c).The black solid lines are given by =,where the domainwall configuration is reduced to single homogeneous bulk with a periodic boundary condition.The magenta dashed lines are given by =-.The red dashed-dotted line in panels (a)—(c) correspond to parameters we use in panels (d)—(f) with =1.5 t2 .(d)—(f) The absolute values of the energy spectrum (upper panels) and various winding numbers (lower panels).In the lower panel,we show the Bloch winding numbers for the left bulk νL (magenta dashed lines) and the right bulk ν R (black dashed lines),as well as non-Bloch winding numbers for the left bulk (red solid lines) and the right bulk (blue solid lines)[44].

此外,我們還發現,即使疇壁某一側的參數不變化,其非布洛赫拓撲數的計算卻依賴于廣義布里淵區,進而會受到另一側參數的影響.例如,圖5(f)中右側區域的非布洛赫拓撲數會在0.16 附近從 0 變化為 0.5,而此時右鏈的參數始終保持不變.這是疇壁邊界條件下的非厄米系統又一個獨特的性質.

4 一維量子行走體系中的非厄米趨膚效應

在第3 節討論的非厄米SSH 模型中,已經從理論上推導了廣義布里淵區和非布洛赫拓撲數,并基于此重新構建了非厄米系統中的拓撲體邊對應關系.但是如何在實驗系統中模擬非厄米趨膚效應并驗證非厄米體邊對應關系,依然是一個重要的問題.本節將介紹如何在一維光量子行走的實驗平臺中模擬具有非厄米趨膚效應的有效哈密頓量,并在該模型中討論廣義布里淵區和非布洛赫拓撲數的計算,再次驗證非厄米體邊對應關系[17].

4.1 模 型

量子行走是一類高度可控的周期驅動系統,被廣泛應用于量子算法[50,51]和量子模擬[52—55]的研究.近些年來,人們開始致力于在離散量子行走平臺中模擬和研究非厄米拓撲相[56—58],這為研究具有非厄米趨膚效應的拓撲非平庸模型提供了一個良好的基礎.

在量子行走系統中,選定如下的非幺正時間演化算符:

通過對角化實空間的時間演化算符,得到了所有的本征態波函數,如圖6(b)所示.可以看到,隨著γ的增加,體態波函數會漸漸局域在疇壁邊界附近.由此可以判斷系統具有非厄米趨膚效應.該模型還具有手征對稱性,σxUσx=U-1,所以也可以在其中探討非厄米拓撲相變和體邊對應關系.接下來將在第4.2 節討論該模型中的廣義布里淵區的計算,在第4.3 節討論非布洛赫拓撲數的計算.

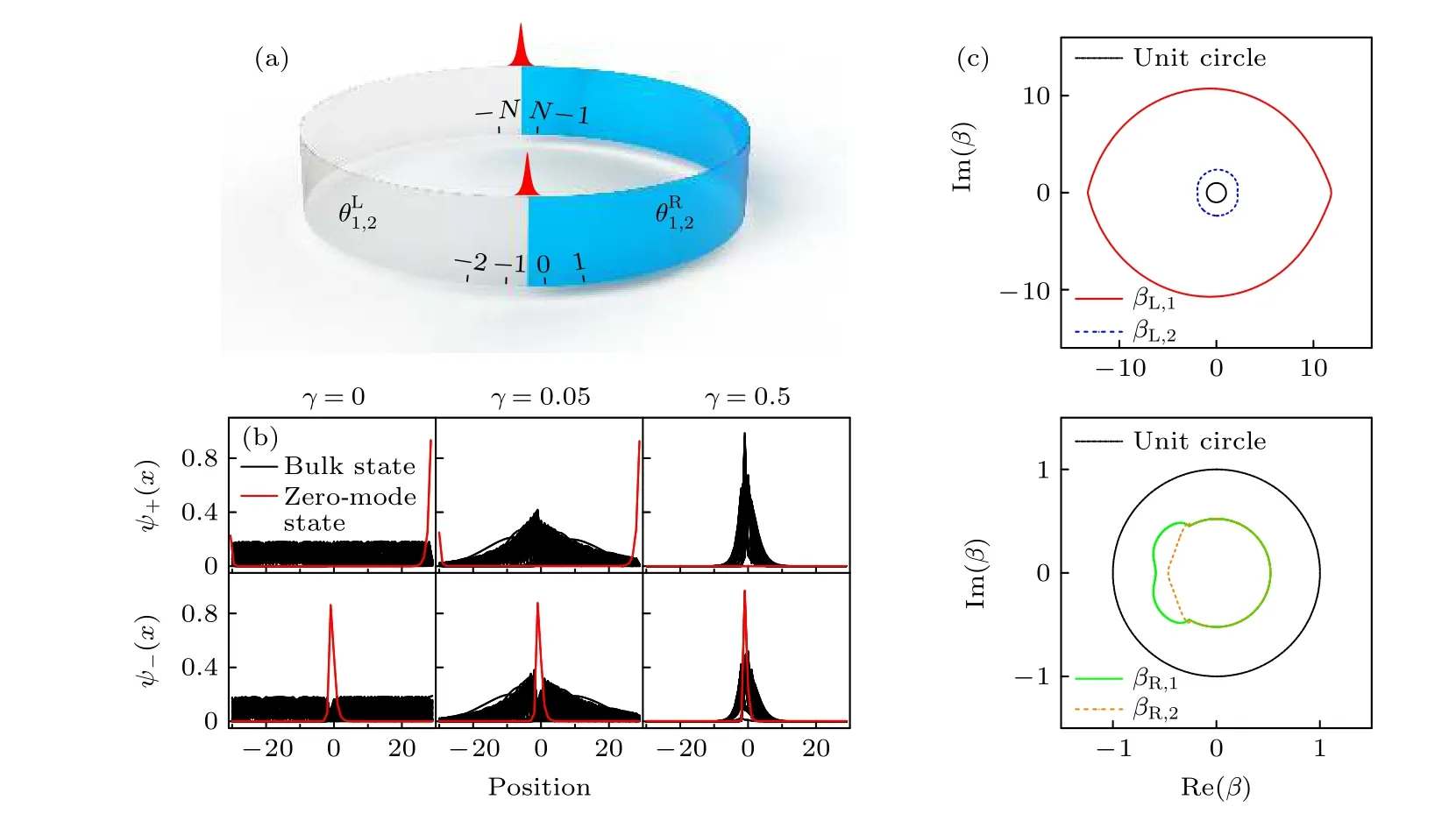
圖6 具有非厄米趨膚效應的量子行走 (a) 疇壁邊界條件示意圖;(b) 體態波函數(黑色)和邊緣態波函數(紅色)的空間分布,其中是手征對稱算符的本征態;(c) 左邊(右邊)區域的廣義布里淵區 β L(R),i,i=1,2 代表 β 有兩支解.標準的廣義布里淵區是單位圓(黑色實 線).參數選取為 N =30 ,=0.1875π,=-0.3333π,=0.2π,=-0.6667π,以及 γ =0.5 [17]Fig.6.Quantum walks with non-Hermitian skin effect: (a) Schematic illustration of the domain-wall configuration.(b) Spatial distribution of the projected norms of bulk (black) and edge (red) states,withare eigenstates of the chiral-symmetry operator.(c) Generalized Brillouin zones for left (right) bulk β L(R),i,i =1,2 indicates two solutions of β .Whereas the standard Brillouin zones are indicated by unit circles (solid black line).Parameters: N =30,=0.1875π,=-0.3333π,=0.2π,=-0.6667π,γ=0.5 [17].

4.2 廣義布里淵區的計算

為了計算廣義布里淵區,先給出波函數本征態的通解形式:

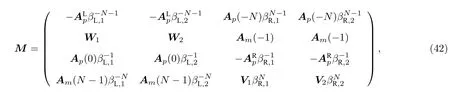
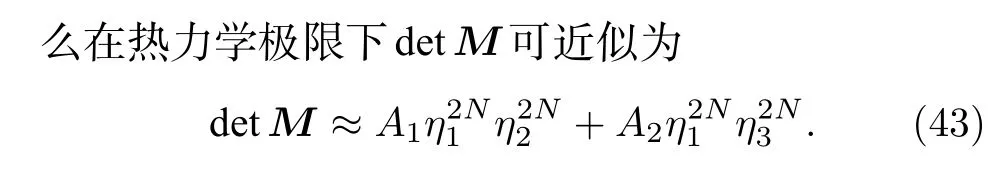
于是便可得到形式上與(29)式完全一樣的廣義布里淵區方程,并可按照3.2 節中的方法求解廣義布里淵區.圖6(c)給出了左右區域廣義布里淵區的例子.

4.3 非布洛赫拓撲數與體邊對應關系

接下來,基于廣義布里淵區,計算量子行走模型中的非布洛赫拓撲數.需要注意的是,量子行走是周期驅動系統,即使是對于傳統的幺正時間演化算符,其拓撲性質與靜態哈密頓量的情況也有所區別.對于靜態哈密頓量,如系統滿足手征對稱性,那么其能譜一定是關于E=0 對稱分布,能隙也一定出現在零能處.但是對于周期驅動的系統來說,其準能量分布在 [-π,π) 區間,如果系統有手征對稱性,那么準能量不僅關于E=0 對稱,也關于E=π對稱,所以拓撲絕緣體的能隙會出現在準能量ε=0 和ε=π 兩個位置.因此當系統處于拓撲非平庸區時,其邊緣態能量會有 0 和 π 兩個模式,相應地,也需計算 0 模和 π 模兩種拓撲數ν0和νπ.關于Floquet 系統中的拓撲理論,在過往的文章中有過很多討論[59—63].這里先對布洛赫拓撲數ν0和νπ的計算方法做簡單介紹.首先可以定義另一個時間框架下的時間演化算符:

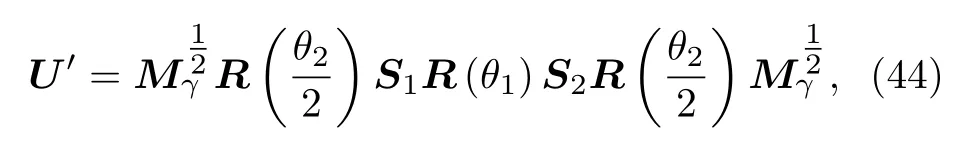
U′和U相當于選取了不同的時間起始點,他們具有相同的準能量能譜,都滿足手征對稱性,對稱性算符均為σx.然后參照(30)式中的方法,分別計算不同時間框架下的布洛赫拓撲數ν和ν′.注意(30)式中的χk和ψk分別是時間演化算符的左右本征矢,定義為

對于傳統的幺正量子行走系統,ν0(π)即可預測系統0(π)模的拓撲邊緣態,但是在本文討論的非幺正量子行走系統中,布洛赫拓撲數并不能正確地刻畫非厄米系統中的拓撲性質,因此,還需根據廣義布里淵區的計算結果和拓撲數的計算公式(32),計算不同框架下的非布洛赫拓撲數和,進而得到0(π)模的非布洛赫拓撲數:

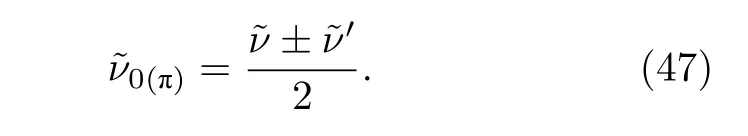
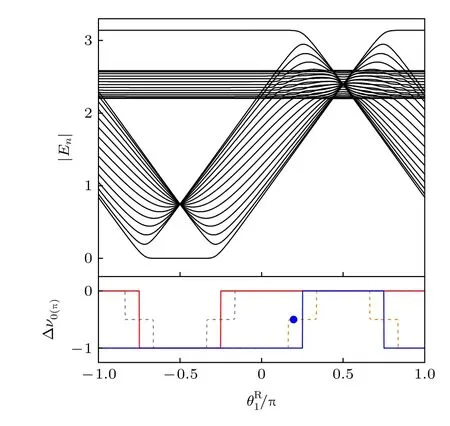
圖7 黑色實線為準能量能譜,紅色實線和藍色實線分別代表零模拓撲不變量的差值和 π 模拓撲不變量的差值;灰色虛線和橙色虛線分別代表左右兩邊零模拓撲不變量的差值和 π 模拓撲不變量的差值;藍色點代表圖8 選取的參數.參數選 擇: =9π/16,=π/4,=3π/4,以 及γ=0.2746[17]Fig.7.Black solid line represents quasienergy spectrum.Red solid line and blue solid line represents zero-mode and π-mode topological invariant difference,respectively.Grey dashed line and orange dashed line represents zero-mode and π -mode topological invariant difference,respectively.The blue dot indicates the parameter for Fig.8.Parameters:=9π/16,=π/4,=3π/4,and γ =0.2746 [17].

4.4 實驗探測邊緣態

前面幾節已經在理論上驗證了非布洛赫拓撲數與非厄米系統中邊緣態的對應關系,但是如何在實驗上探測非厄米系統中的邊緣態依然是一個具有挑戰性的問題.由于非厄米趨膚效應的存在,邊緣態的波函數分布和體態波函數一樣,都是局域在邊界上,因此很難通過直接測量波函數在實空間分布的方法識別出拓撲邊緣態.為了克服這一困難,我們通過對每一步時間演化的波函數加權求和的方法直接將邊緣態模式提取出來.具體方法如下.首先定義

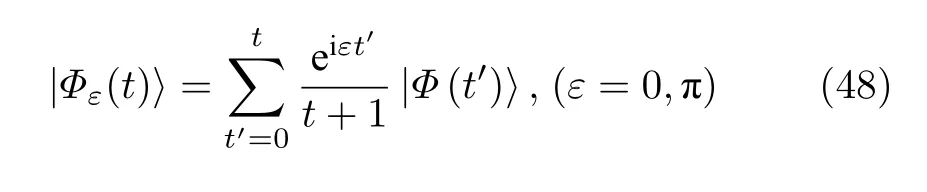
然后,把含時演化的波函數在本征態上做展開,得到

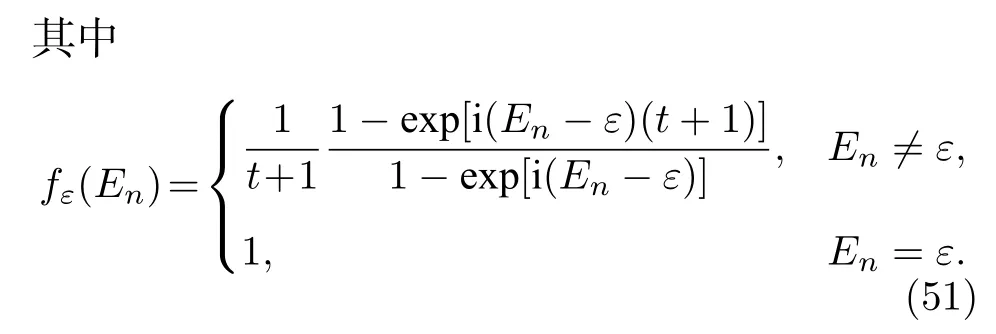
如果準能量能譜為純實數時,那么對于Enε的本征態,其加權系數也就是說只要時間演化足夠長,加權求和的波函數|Φ0,π(t)〉中只會留下能量為En=0,π 的本征態,也就是0 模和 π 模的拓撲邊緣態.需要注意的是,在非幺正量子行走系統中,準能量能譜不一定總是純實數,所以需要選取準能量為純實數的參數區間進行探測.

圖8 給出了將該方法應用到實驗上得到的觀測結果.在拓撲不變量滿足=(0,-1) 的參數點,對于不同的初態選取,實驗上都探測到了Φπ,+(x)的模式,并且其他模式占據很小.圖8(d)—(f)中也將觀測所得到的Φπ,+(x) 與實空間數值對角化得到的邊緣態模式波函數做了對比.由兩者相符可以看出Φπ,+(x) 的確提取到了ε=π 的本征邊緣態模式.在實驗上觀測得到的拓撲邊緣態與非布洛赫拓撲不變量一致,這也再一次印證了基于廣義布里淵區構建的非厄米拓撲體邊對應關系.

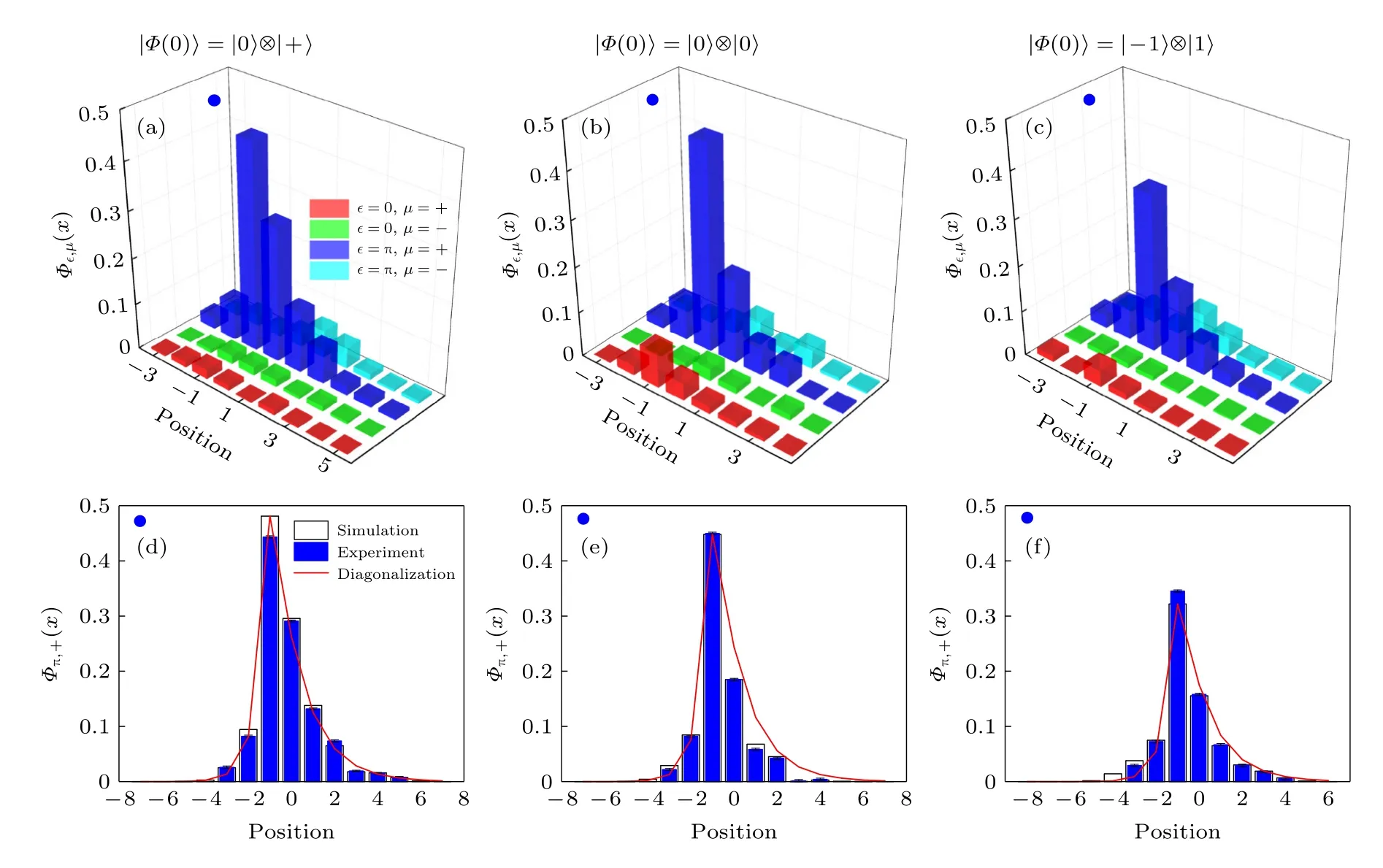
圖8 (a)—(c) 不同初態選擇下,7 步演化之后實驗測量得到的 Φ ε,μ(x) ; (d)—(f) 數值模擬得到 Φ π,+(x) 和實驗結果的對比.圖中還給出了數值對角化 N =15 的疇壁系統對峰值進行縮放之后的結果.對角化得到的邊緣態進行縮放的比例通過擬合Φπ,+(x)的中心峰值得到.其他參數與圖7 相同[17]Fig.8.(a)—(c) Experimentally measured Φ ε,μ(x) after the seventh step with different initial states;(d)—(f) simulated Φ π,+(x) compared with experimental result.We also show the scaled norms of the edge state with ε =π by diagonalizing a domain-wall system with N =15 .Norms of the edge states from diagonalization are scaled to fit the central peak of the numerically-simulated Φ π,+(x) .Other parameters are as same as Fig.7[17].

5 總結與展望

本文主要介紹了疇壁邊界條件下具有非厄米趨膚效應的系統中廣義布里淵區方程的推導與求解,并由此出發討論了非布洛赫能帶理論在非厄米SSH 模型和非幺正一維量子行走實驗模型中的應用.基于廣義布里淵區計算的非布洛赫拓撲數可以正確預測疇壁系統中的拓撲邊緣態,這印證了非布洛赫能帶理論在不同邊界條件下非厄米系統中的有效性.在不同模型中,疇壁邊界條件下的廣義布里淵區方程有一個統一的方程形式,對該方程背后物理內涵的充分理解,或許可以幫助我們找到一個對多種邊界條件都普適的廣義布里淵區方程.此外,不同邊界條件下的高維系統中,廣義布里淵區的計算分析也尚未被充分討論,有待于日后進一步探索.