基于Aharonov-Bohm 籠的非厄米趨膚效應抑制現象*

陳舒越 蔣闖 柯少林? 王兵? 陸培祥

1) (華中科技大學物理學院,武漢 430074)

2) (武漢工程大學,光學信息與模式識別湖北省重點實驗室,武漢 430205)

能帶理論在光學領域的應用為控制光傳輸提供了有效手段,非厄米趨膚效應的發現擴展了傳統能帶理論的范疇,能夠實現新型光局域和單向傳輸現象.然而在光學體系,如何有效地產生并調控非厄米趨膚效應仍然是重要的研究主題.本文研究了具有規范勢的準一維菱形光晶格中的非厄米趨膚效應,通過計算本征能譜、環繞數和模式演化特性,發現規范勢能夠對趨膚效應強弱進行有效調節.當規范勢大小為π 時,趨膚效應被完全抑制,而由Aharonov-Bohm 籠效應引起的平帶局域占主導.利用間接耦合微環諧振腔陣列,可同時產生合成光子規范勢和非對稱耦合,為研究Aharonov-Bohm 籠和趨膚效應的競爭機制提供了可能的實現方案.本研究結果為利用規范勢調控趨膚效應提供理論基礎,在發展片上非磁性單向傳播器件也具有潛在的應用前景.

1 引言

光的傳輸和局域調控是發展下一代集成光子芯片的重要基礎,能有效應對信息處理和計算能力日益增長的需求.隨著對光子晶體[1]、光波導陣列[2]和合成光子晶格[3]等光學體系的深入研究,光子調控的手段變得更加豐富.例如,通過能帶工程,可以實現如衍射管理[4]、負折射[5]、無衍射傳輸[6]、布洛赫震蕩[7]等豐富的光束控制;也可實現不同類型的光波局域,如動態局域[8],平帶局域[9,10],摩爾晶格局域[11].而能帶理論和拓撲的結合發展出了拓撲光子學這一新領域,基于量子霍爾效應[12]、量子反常霍爾效應[13]、谷自旋[14]等效應的光學類比,能構建具有拓撲保護、抵抗擾動的單向光波輸運,有效抑制制造缺陷和無序擾動引起的背向散射問題[15];此外,利用拓撲界面態,拓撲角態等也可實現抵抗擾動的光局域,應用于拓撲激光等[16,17].

近年來,能帶理論的研究推廣至非厄米系統,對具有非對稱耦合的一類格點系統的研究發現,在開放邊界條件下,系統的體態與拓撲邊界態都局域于結構邊緣,這一新奇現象被命名為非厄米趨膚效應[18].非厄米趨膚效應的發現給傳統能帶理論帶來了發展,同時也為控制光局域和單向傳輸提供了新途徑[19,20].首先,非厄米系統的能隙擴展為點能隙和線能隙,系統的對稱性也變得更為復雜[21].其次,在這類系統中,開放邊界條件與周期邊界條件下的能譜呈現完全不同的特性,布洛赫能帶圖像不能準確刻畫體態性質.更為重要的是,拓撲能帶理論中,傳統的體邊對應關系受到了極大的挑戰;在開放邊界條件下存在的拓撲邊緣態或界面態,其性質由系統的體態特性所決定,這種全息關系叫作體邊對應;然而,由于趨膚效應,體態局域于邊界,常規的拓撲不變量無法準確描述拓撲非平庸邊界態的性質,導致體邊對應關系的破缺.為解決這一問題,人們發展了能譜拓撲、廣義布里淵區和非布洛赫拓撲不變量,成功預測了非厄米趨膚效應的產生條件和拓撲邊界態的出現與消失,重構了非厄米系統中的體邊對應關系[18].目前,非厄米趨膚效應在凝聚態[22]、冷原子[23]、電路[24]、聲學[25]和機械振動[26]引起了廣泛的研究興趣.

在光學體系中,如何產生和調控非厄米趨膚效應是重要的研究課題,最基本的方法是產生非對稱耦合.利用光纖環路可以實現等效的時間、頻率晶格[7,27],利用放大器構建非對稱耦合進而實現合成維度的趨膚效應[28].在間接耦合微環諧振腔陣列中,在連接微環中一半周期引入增益,另一半引入損耗,構建傳輸路徑依賴的等效耦合,同樣能夠實現非對稱耦合[29].此外,利用磁性或各向異性光子晶體,規范勢和增益損耗相互作用,反射波干涉等手段,不直接產生非對稱耦合也可實現趨膚效應[30].此外,趨膚效應和其他局域模式和物理效應的相互作用也是重要的研究課題.例如,隨機擾動引起的安德森局域和非厄米趨膚效應可以產生多種相變[31];在二維體系中,拓撲和非對稱耦合產生雜化趨膚模,磁場對趨膚效應會產生抑制作用[32];在一維體系中,利用時變電場產生動態局域,也可以控制趨膚效應[33].其他物理效應和趨膚效應相互作用會有哪些新現象,特別是在集成光學體系,其作用又會給光操控帶來哪些機會?

本文擬研究準一維菱形晶格中的規范勢和非厄米趨膚效應的相互作用.通過計算本征能譜和環繞數,發現規范勢能夠對趨膚效應的強弱進行有效調節.當規范勢大小為π 時,周期邊界和開放邊界條件下的能譜演變為平帶并且重新重合,趨膚效應被完全抑制,而由Aharonov-Bohm 籠效應(Aharonov-Bohm cage,AB 籠)引起的平帶局域占主導,從演化特性可以觀察到從趨膚模式向平帶局域模式的變化情況.進一步提出利用間接耦合微環諧振腔陣列,可以同時產生規范勢和非對稱耦合,并利用傳輸矩陣法詳細分析了耦合特性,模擬仿真了光場分布和透射譜,為研究AB 籠和趨膚效應的競爭機制提供了可能實驗方案.本文的研究成果為利用規范勢調控趨膚效應提供了途徑.

2 理論模型

2.1 緊束縛模型和本征能譜

考慮如圖1 所示的菱形晶格,每個單元包含A,B,C三個格點,只考慮最近鄰耦合.同一個晶胞中A和B格點以及C和相鄰晶胞A格點的耦合為非厄米非對稱耦合(紅色和綠色箭頭),同時,每個晶胞具有大小為φ的規范勢,可以由A和C格點耦合系數中的非互易相位引入(黃色虛線).該晶格在實空間的哈密頓量為

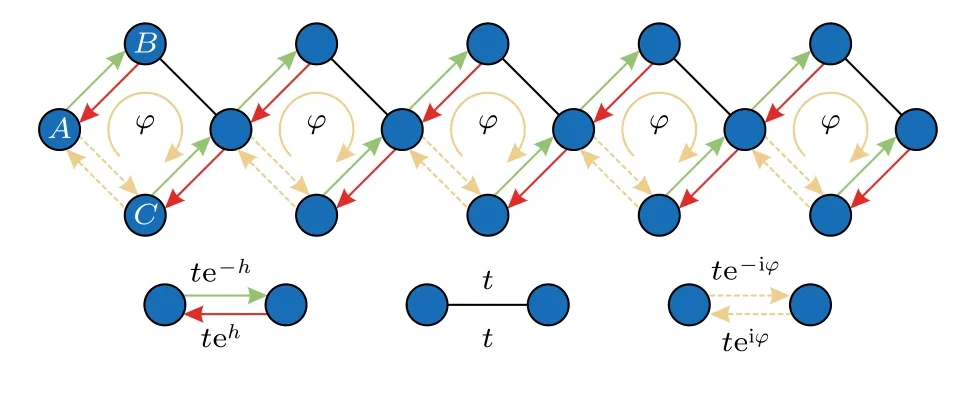
圖1 準一維非厄米菱形晶格示意圖Fig.1.Schematic of non-Hermitian quasi-one-dimensional rhombic chain.

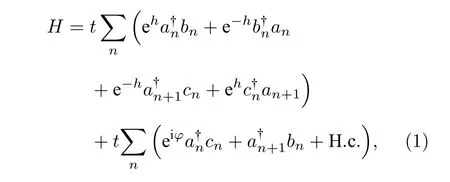
其中,t為耦合系數;h為虛規范勢,導致非對稱耦合,h越大非對稱度越大.

周期邊界條件下,系統的哈密頓量為

其中,k為布洛赫動量.由于存在非對稱耦合,系統會出現趨膚效應,模式會趨向局域于結構邊緣處.局域方向由h的符號決定,h＞ 0 時,向左耦合系數大于向右的耦合,出現左趨膚效應;而h＜ 0 的情況相反.此前對菱形晶格的研究已表明,厄米情況下,當規范勢大小為φ=π 時,由A格點耦合到相鄰A格點的波經過B和C兩條路徑發生相消干涉,形成AB 籠效應,此時,能帶退化為無色散的平帶,體態變為緊湊局域態[34,35].

因此,為理解調節規范勢對趨膚效應的影響以及其之間的相互作用,首先考慮厄米情況,即h=0.圖2(a)—(c) 所示為不同規范勢取值情況下的能譜,計算中選取的總格點數N=61,結果顯示,周期邊界和開放邊界條件下的能譜重合在一起,此時系統都不支持趨膚效應.而當φ=π 時,發生相消干涉,體帶退化為3 個平帶,對應復平面上3 個點E=0,±t,如圖2(c)所示.此外,復平面上存在能量為的點,是開放邊界條件下的拓撲邊界態,其拓撲不變量為半整數[36].

引入非對稱耦合后,一般情況下,系統能譜對邊界條件很敏感,周期邊界條件下能譜和開放邊界的不再重和,如圖2(d)所示,選取的參數h=0.6,φ=0 和t=1.在復平面上,周期邊界條件下的能譜為有面積的閉合曲線,具有非厄米點能隙,而開邊能譜則退化成弧線并且被周期邊能譜所包圍,此情況下,開放邊界條件下系統具有趨膚效應,其出現條件可以根據周期邊界的拓撲譜環繞數來預測,定義為[37,38]

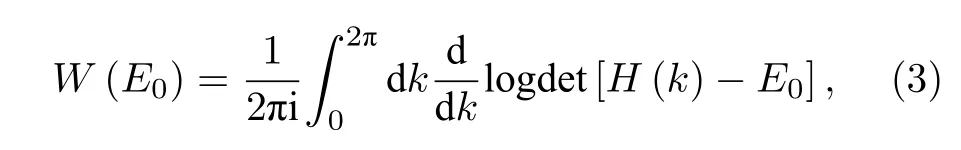
式中,k為布洛赫動量,E0為任意基準點.存在趨膚效應的充要條件為存在E0∈C使得W(E0) ≠ 0.當周期邊為閉合曲線時,選取E0為閉合曲線內部點,則W(E0) ≠ 0;而無趨膚效應時,周期邊能譜塌縮成一條弧線,不存在內部點,W(E0)=0.進一步將規范勢大小改變為φ=0.5π,如圖2(e)所示,仍然能觀察到周期邊界條件下的能譜是閉合曲線,周期和開放邊界條件下不一致,但周期邊能譜圍繞的面積顯著減小.規范勢增大為φ=π 時,如圖2(f)所示,周期邊界能譜塌縮為平帶,不再具有內部面積,并且和開邊能譜重合,此時系統不再具有趨膚效應.通過對角化H(k),求解出周期邊能譜為E=0,±2t,和耦合系數非對稱度大小無關,并且和厄米情況保持一致.因此,當出現AB 籠效應時,趨膚效應被完全抑制.

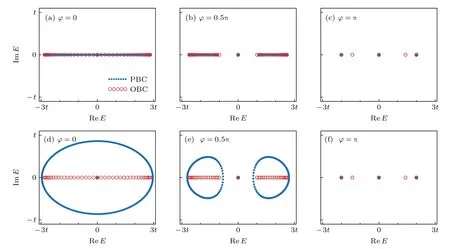
圖2 周期邊界條件(藍色實心圓)和開放邊界條件(紅色空心圓)下的復能譜 (a)—(c) 分別對應厄米情況下(h=0)規范勢 φ=0,0.5π,π 的能譜圖;(d)—(f) 分別對應非厄米情況下(h=0.6)規范勢 φ=0,0.5π,π 的能譜圖Fig.2.Complex energy spectra under periodic (blue solid circles) and open boundary conditions (red hollow circles): (a)—(c) Energy spectra for Hermitian cases (h=0) with φ=0,0.5π,π,respectively;(d)—(f) energy spectra for non-Hermitian cases (h=0.6) with φ=0,0.5π,π,respectively.

2.2 趨膚效應及演化分析

以上討論的能譜特征可用來預測趨膚效應,而從本征模式分布可更直接觀察趨膚模式.圖3(a)—(f)所示為不同規范勢φ和非對稱耦合系數h下的模式分布圖,其中,模式編號按能量實部從小到大排列.首先考慮規范勢φ=0 時的情況,由于h=0,無趨膚效應,模式在整個結構的格點都有分布,如圖3(a)所示.而當h增大時,系統具有非厄米非對稱耦合,所有模式都局域于結構的左邊界處,而遠離邊界呈現指數衰減的特性,即出現趨膚效應,如圖3(b)所示.隨著h進一步增大,如圖3(c)所示,趨膚效應強度變得越來越強,模式的局域性進一步增強.值得一提的是,從圖3(b),(c)還可發現,中等能量大小附近的模式在非對稱耦合系數h不為0 時,并未表現出明顯的趨膚效應,這是由系統本身的能帶結構所決定的.可知準一維菱形鏈的能帶是由一條無色散的零能平帶和兩條色散帶組成,只有當規范勢φ=π 時,兩條色散帶退化為平帶,才形成了具有三條平帶的能帶系統[34];通過圖2也可以發現,無論規范勢φ和非對稱耦合系數h取何值,始終存在零能帶(Re(E)=Im(E)=0).即無論φ和h取何值,都始終存在一條E=0 的零能平帶,能量低且無色散,使其對應模式的趨膚效應并不明顯.而對于規范勢φ=π 的情況,發生AB 籠效應,體態模式演化為緊湊局域模式,如圖3(d)所示;在非對稱耦合系數不是很大時,隨著當h增大,本征模式并沒有向左邊緣局域,而仍然為緊湊局域模式,如圖3(e),(f)所示,這充分說明了AB 籠效應對趨膚效應的有效抑制.為了定量表征模式的局域性,通過數值計算了MPR(mean participation ratio),其定義為[39,40]

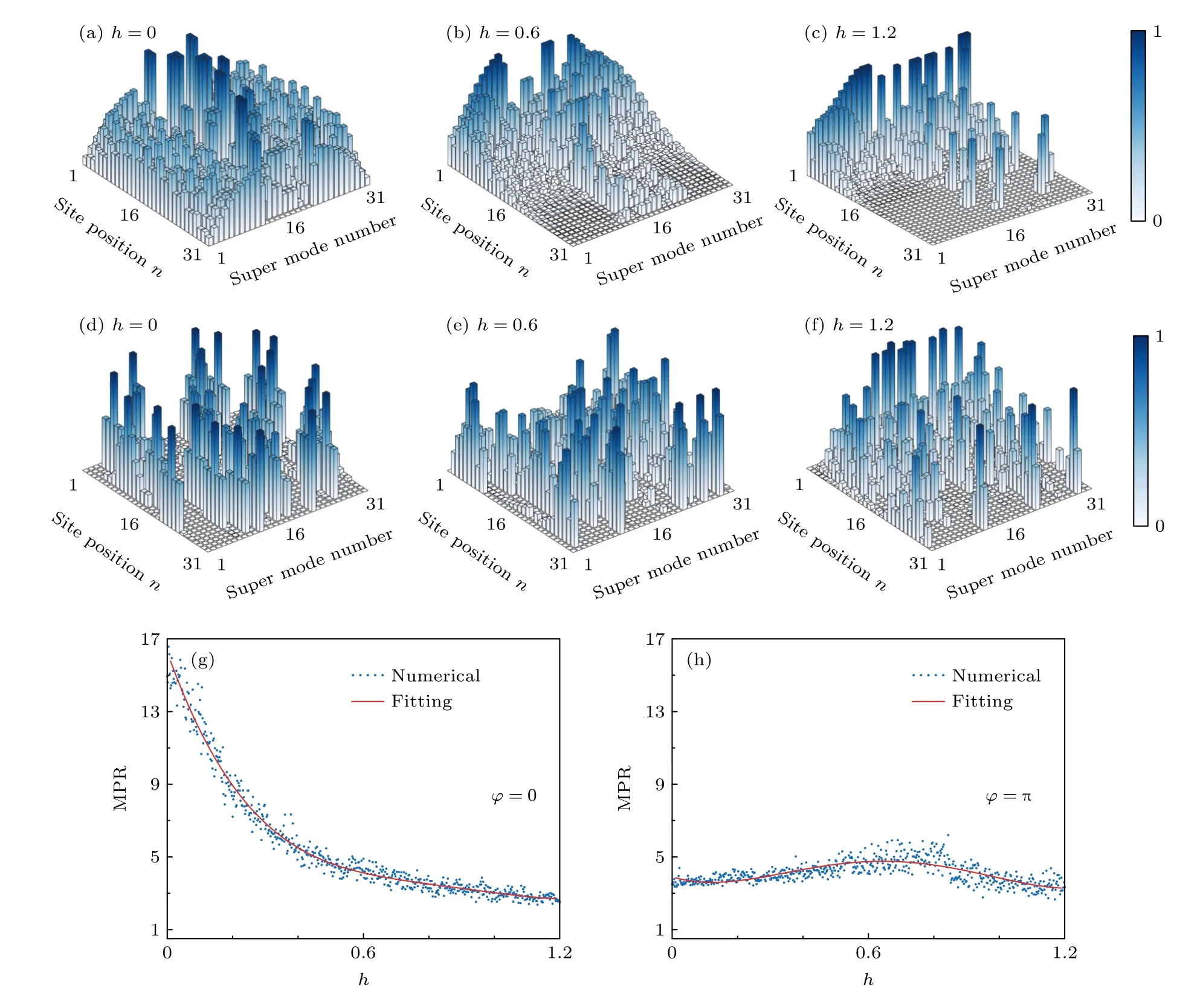
圖3 不同參數下的本征模式分布和MPR 變化 (a)—(c) φ=0 時,h 取0,0.6,1.2 時的本征模式分布;(d)—(f) φ=π 時,h取0,0.6,1.2 時的本征模式分布;(g) 規范勢 φ=0 時MPR 隨h 變化情況;(h) 規范勢 φ=π 時MPR 隨h 變化情況;藍色圓點表示數值計算的結果,紅色實線表示回歸分析的結果Fig.3.The distribution of eigenmodes and the variation of MPR via h under different parameters: (a)—(c) the distributions of eigenmodes with φ=0 as h=0,0.6,and 1.2,respectively;(d)—(f) the distributions of eigenmodes with φ=π as h=0,0.6,and 1.2,respectively;(g) MPR as a function of h for φ=0;(h) MPR as a function of h for φ=π.The blue dots indicate the result of numerical calculation and the red solid lines indicate the result of regression.

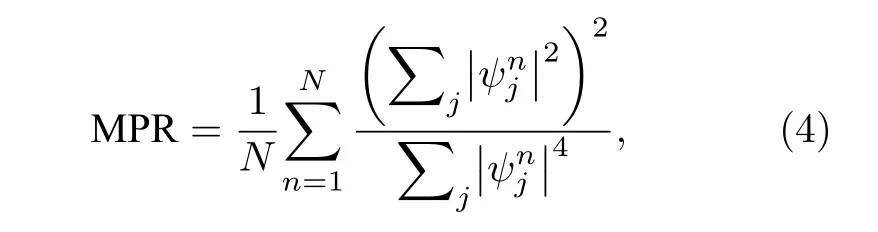
其中,j為節點編號,n為模式編號,表示第n個本征模式在第j個節點上的分布大小.MPR 值越大,模式越不局域;MPR 越趨于1,模式越局域.圖3(g)描述了φ=0 情況下MPR 隨耦合非對稱度h的變化關系,藍色點為數值計算結果,為了更好地描述變化趨勢,也給出了基于四次多項式擬合的擬合結果,如紅色曲線所示.在此情況下,MPR隨著非厄米耦合的非對稱度增大而減小,表明模式的局域性逐漸增強,即趨膚效應的增強.而當φ=π,情況不同,首先,由于AB 籠的效果,體態變為緊湊局域態,局域于結構不同位置,即使厄米情況,MPR 也較小,約等于3.5;隨著h增大,MPR 數值變化并不明顯,并沒有發生單調減小的情況,這是由于緊湊局域態并沒有由于非對稱耦合而打破.因此,由于AB 籠效應,趨膚效應被有效抑制.

從模式演化能更清楚地觀察趨膚效應及AB籠效應.圖4 描述了不同規范勢和非對稱度情況下的模場演化結果圖.計算中選取了格點總數目為N=31,初始態為Ψ(16)=1,其他格點為0.當φ=0,厄米情況時,無趨膚效應,可以觀察到呈現對稱演化情況,如圖4(a)所示;當h=0.6 時,為左趨膚效應,模式趨于向節點編號N較小值演化,到達邊界后,局域于邊界處,如圖4(b)所示;而當h=—0.6 時,趨膚效應方向也相應反過來,模式趨于向節點編號較大值演化,如圖4(c)所示.而對于φ=π 情況,AB 籠效應占主導,無論h取多大值,模式呈現平帶局域,分布于入射端口相鄰節點,趨膚效應被抑制,如圖4(d)—(f)所示.

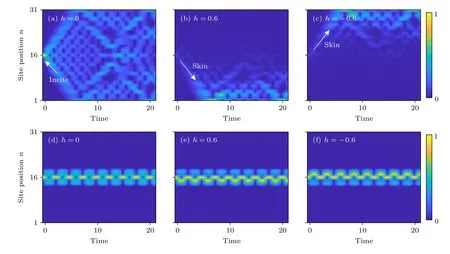
圖4 不同參數下的單點激發隨時間演化特性 (a)—(c) 規范勢 φ=0 時h 分別取0,0.6,—0.6 時的演化;(d)—(f) 規范勢 φ=π 時h 分別取0,0.6,—0.6 時的演化Fig.4.Time-dependent wave dynamics for single-site injection with different parameters: (a)—(c) For φ=0 with h=0,0.6,—0.6,respectively;(d)—(f) for φ=π with h=0,0.6,—0.6,respectively.

接著,從模式演化的角度來定量的描述φ趨于π 的過程中趨膚效應的變化情況,計算了系統在單點激發下,輸出模式分布隨規范勢的變化情況,如圖5 所示.可以清楚地觀察到,在規范勢φ＜0.8π 時模場表現出顯著的趨膚效應,到達邊界后并局域在邊界處.在規范勢0.8π ＜φ＜ 0.95π 時,趨膚效應變得較弱,模場未演化到邊界;并且從圖5可以發現,趨膚效應的強度也會隨著規范勢φ的變大而逐漸變弱.在規范勢φ＞ 0.95π 時,可以看出,此時趨膚效應已經幾乎被抑制,沒有顯示出向邊界演化的趨勢,AB 籠效應帶來的局域效果占主導地位,模場被局域在入射端口處的一個原胞內.由此可以看出,在單點激發下,模場演化的趨膚效應會隨著規范勢φ的變大逐漸減弱,而在φ＞ 0.95π時,趨膚效應基本被抑制,從而便可以得到良好的趨膚效應抑制效果.

圖5 單點激發下一段時間演化后(時間取20)的輸出模場分布隨規范勢φ 的變化情況.格點總數N=31,激發位置始終位于結構的正中間A 格點(n=16),選取固定不變的趨膚強度h=0.6,模場強度已做歸一化處理Fig.5.The variation of the output field distribution with the gauge potential φ after a period of evolution under single-site excitation (Time is 20).The total number of site N=31.The field is incident from the middle A site of the structure (n=16),the skin strength is fixed at h=0.6,and the intensity of the field is normalized.

3 模擬結果

3.1 微環諧振腔耦合分析

利用間接耦合微環諧振器陣列可以實現規范勢和非對稱耦合,為上述規范勢和趨膚效應的相互作用提供可實現的集成光學方案[41,42].通過傳輸矩陣法可以推導微環之間的耦合關系,為簡單起見,考慮如圖6(a)所示的一維晶格,相鄰主環通過連接環相耦合,主環和連接環的長度分別記為L和L+ΔL.其中,連接環設置額外的長度ΔL,可以使得連接環的共振頻率與主環的共振頻率不同,用以控制主環之間的耦合.連接環的上下半周分別引入了增益和損耗,增益損耗系數記為h,同時也引入了傳播相位差,記為φ,分別通過紅色和綠色來表示.每個環都支持兩種模式,包括順時針(CW)和逆時針(CCW)模式.例如,相鄰CCW 模式的主環是通過連接環中CW 模式相耦合.主環與連接環之間耦合的散射矩陣為

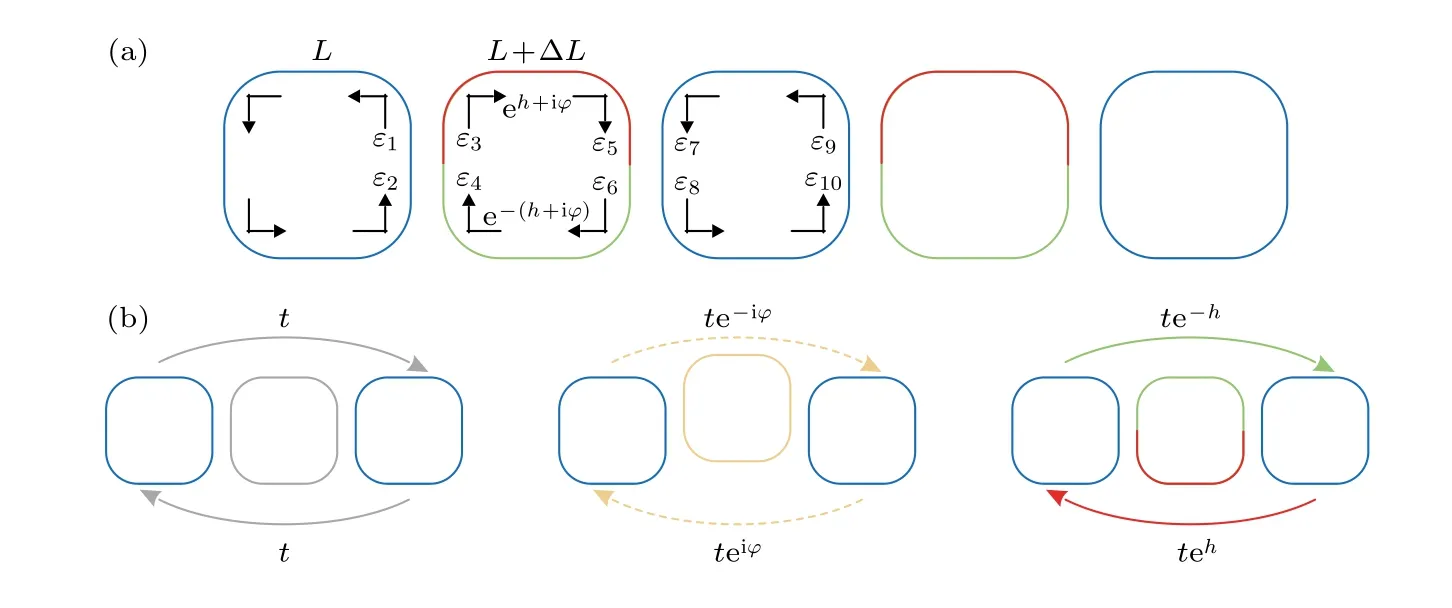
圖6 微環耦合特性示意圖 (a) 一維環形諧振腔陣列演示傳輸矩陣法的原理示意圖;(b) 利用連接環實現不同類型的耦合Fig.6.Schematic diagram of microring coupling characteristics: (a) Schematic diagram of the 1D array of ring resonators to demonstrate the principle of the transmission matrix method;(b) implementation of different types of coupling using link rings.

再將光在連接環中的傳播考慮進去后可得到:

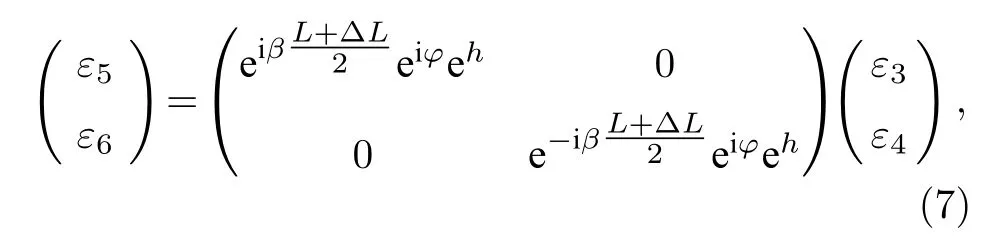
接著,寫出剩余需要的傳輸矩陣:

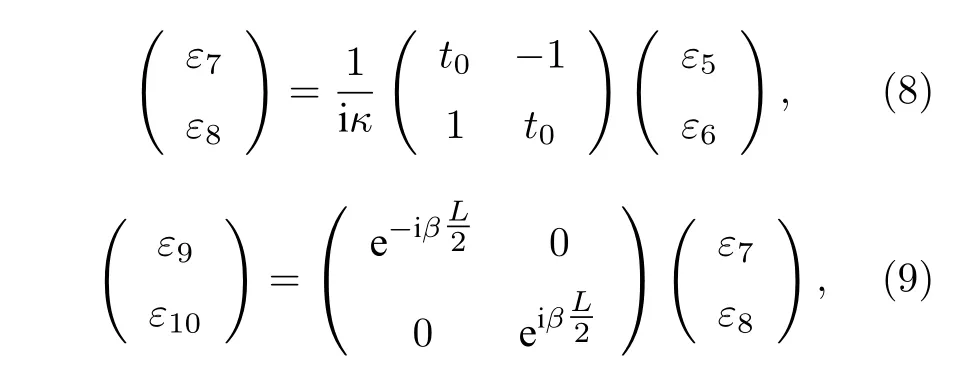
并將它們全部聯系起來后得到

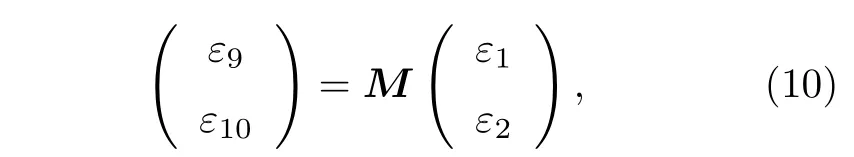
其中M為傳輸矩陣.考慮周期條件,結合布洛赫定理存在非零解的條件為

其中,k為布洛赫動量.當連接環反諧振時,其額外長度ΔL=π+2mπ,將其代入(11)式并化簡可得到色散關系:

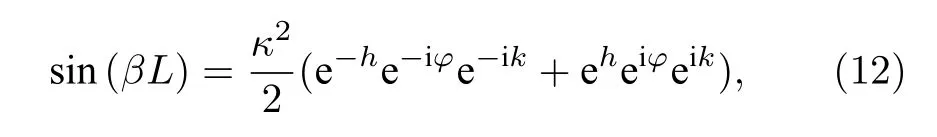
由于主環是共振的,滿足

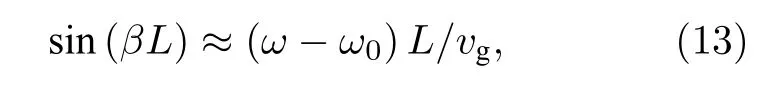
其中,ω0和vg分別表示諧振頻率和群速度,而β則表示傳播常數.色散關系化簡為

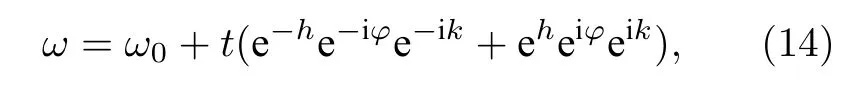
其中,等效耦合系數t=vgκ2/(2L).可以看出傳播相位差φ引入了非互易相位,等效實規范勢;而增益損耗系數h引入虛規范勢,導致非厄米非對稱耦合.

圖6(b)描述了通過在主環之間設置不同類型的連接環來實現不同類型的等效耦合系數.不引入增益損耗和相位差直接在主環之間引入強度為t的耦合,其強度則可以通過環之間的間距來控制.黃色連接環表示通過垂直移動連接環,使得從左到右和從右到左傳輸的光會經歷不同的路徑長度,產生的規范勢大小為φ=2βη=2neffk0·η,其中η為垂直移動位移,neff表示環內的有效折射率,k0表示真空中的波矢.紅、綠色的連接環則表示分別在連接環的上下半周中引入了增益(紅色)和損耗(綠色),誘導出了與方向相關的放大與耗散,從而導致了非厄米的非對稱耦合.

3.2 微環諧振腔中趨膚效應及抑制現象

利用諧振環陣列來驗證準一維菱形鏈中的非厄米趨膚效應及其抑制現象,并通過基于有限元方法的數值仿真軟件COMSOL 進行全波仿真,其幾何結構如圖7(a)所示.在該菱形鏈的中間和兩端分別放置了端口S1,S2 和S3,其中,S1 為輸入端口,S2 和S3 為輸出端口.模擬中,芯層和包層的折射率分別為ncore=3 和nair=1,且每個環芯層的寬度w固定為0.27 μm.這樣的設計是為了在單個環的共振頻率為f0=190.694 THz 時,波導內僅支持有效折射率neff=2.465 的單個TE 偏振模式.主環的邊長L0=10 μm,并在其4 個角設計了半徑r=3 μm 的圓角.連接環相對主環具有額外的長度ΔL=π/(neffk0),這是為了讓連接環滿足反諧振條件.微環之間的間隙g=0.375 μm,由此來確保環與環之間的弱耦合.增益和損耗是通過給連接環的折射率設置虛部,其大小設置為γ=0.007.從S1 端口激發的單頻光為f=190.675 THz,這是因為當規范勢φ=π 時形成的一維AB 籠的能帶結構為3 條平帶,由此在利用該諧振環陣列結構進行仿真過程中,在單個諧振環頻率f0=190.694 THz附近還存在兩處能夠激發E=—2t,2t這兩條體帶的吸收峰.經計算,分別為f1=190.675 THz 和f2=190.725 THz.選取這3 處峰值頻率附近的光,可以使打入該結構中的光盡可能達到最大,展示出的光場效果更佳.在下文仿真中,皆采用了第1 個吸收峰值處的頻率,f=190.675 THz.圖7(b)—(g)分別繪制了當規范勢φ和用于引入增益損耗的折射率虛部γ取不同值時光場的空間分布圖,通過S1端口激發.通過圖7(b),(c)可知,在沒有引入增益損耗時,光場會在φ=0 時擴散到整個系統中,而在φ=π 時則會被束縛在入射端口S1 附近.另一方面,在引入增益損耗γ=0.007 后,繪制出了S2端口處的透射率隨規范勢φ的變化趨勢,如圖7(h)所示,可以清楚看到S2 端口處的透射率T,隨著規范勢φ的變大而逐漸減小,說明其趨膚效應也在逐漸減弱,直至被完全抑制.圖7(d)—(g)繪制了透射譜中紅色圓圈處所對應的模場分布,可以清楚看到,在規范勢φ=0 時向右的趨膚效應十分明顯,模場分布在右邊界處,其對應的透射率最大,約為1;φ=0.8π 時,趨膚效應較弱,模場分布在入射端口右側,大約為T=—15 dB;φ=0.95π 時,幾乎沒有展現出趨膚效應,主要的模場已經呈現平帶局域現象,此時的透射率T≈ —22 dB;當φ=π 時,趨膚效應被完全抑制,光被局域在入射端口S1 附近,T=—40 dB.由此說明,仿真結果與上述的理論預測基本吻合,即該結構的趨膚效應在φ=0 時最強,而后隨著φ的增大而逐漸減弱,并在φ=π 時因為AB 籠效應使光被局域在入射端口附近,完全抑制了趨膚效應;另一方面,可以看出,在φ=0.95π 時便已經可以獲得良好的趨膚效應抑制現象.

圖7 耦合微環諧振腔陣列的趨膚效應模擬結果 (a) 菱形微環諧振腔陣列示意圖;(b)—(g) 分別展示了規范勢φ 和用于引入增益損耗的折射率虛部大小γ 取不同值時的模場強度空間分布(|E|2);(h) S21 隨φ 的變化趨勢Fig.7.Simulation results based on coupled resonator arrays: (a) Geometry of non-Hermitian quasi 1D rhombic chain with ring resonator arrays;(b)—(g) the spatial intensity(|E|2) distributions of light with different values of gauge potential φ and the imaginary index γ used to introduce gain and loss;(h) the trend of S21 with φ.

4 結論

本文研究了具有合成光子規范勢的準一維菱形光晶格中的非厄米趨膚效應.該結構中具有兩種局域模式,由非對稱耦合引起的趨膚模式,局域于結構的邊緣處;當規范勢φ=π 時,由Aharonov-Bohm 籠效應引起的平帶局域,束縛于任意入射端口及相鄰節點.另一方面,通過分析發現,在規范勢φ從0 逐漸變化至π 的過程中,趨膚效應會逐漸減弱,直至φ=π 時被完全抑制;其中在φ＞0.95π 時,便已經可以得到良好的趨膚效應抑制效果.因此,利用二者的競爭關系,能夠通過改變規范勢對趨膚效應的強弱進行有效調節,這可以從本征能譜、環繞數和模式演化特性反映出來.利用傳輸矩陣法分析了間接耦合微環諧振腔陣列的耦合特性,指出產生規范勢和非對稱耦合的方法,模擬仿真了規范勢對趨膚效應的調控作用.本文的研究局限于平帶局域和趨膚效應的相互作用,此晶格中還存在拓撲邊界局域模式,該局域和趨膚效應的作用還有待進一步探索;微環陣列能夠構建二維光晶格,存在更多類型的局域模式,不同模式之間的相互作用也值得深入研究.總之,本文的研究結果為一維晶格中利用規范勢控制趨膚效應提供了理論方案,為設計緊湊的非磁性單向傳播光器件也具有實際的應用價值.