基于改進分段截斷二次速度軌跡模型的行程時間估計*
□ 陳詩意,潘義勇,魏雙秋
(南京林業大學 汽車與交通工程學院,江蘇 南京 210037)
行程時間是描述交通狀態的重要指標,是出行者和交通管理者的決策依據[1-2]。由于城市交通環境下的出行極容易受到外部因素的影響,因此研究可靠的行程時間估計模型對交通管理和路徑誘導有重要的意義[3-5]。目前行程時間的估計模型主要分為基于交通流理論的模型、基于數據的模型和混合模型三大類[6]。基于交通流理論的估計模型受限于參數和特定系數,可移植性較差。混合模型結合了歷史和實時估計,雖然不需要進行參數估計,但歷史和實時估計各自的重要度和影響程度卻難以確定[7]。因此,更多行程時間估計的相關研究選擇是基于數據的模型的。流量和占有率等交通流特征數據依賴于高精度的探測設備和識別系統,故目前基于數據的行程時間估計模型多采用速度數據來進行建模研究。
基于速度的行程時間估計模型一般利用速度-時間的關系構造模型。Li等[8]提出的瞬時速度模型和時間切片模型,分別考慮了速度在空間上的變化和速度在離散時間上的變化。Cortés等在瞬時速度模型的基礎上提出了改進的動態時間切片模型,提高了模型估計的精度。但以上兩種模型是以上下游路段節點同一時刻的速度平均值來計算行程時間的,沒有考慮行程過程中速度隨時間的變化,不符合現實中車輛在路段上速度變化的情況[9-10]。Van 等[11]提出的線性模型將上下游路段節點之間的速度表示為車輛所處位置的距離線性函數,雖然構造的速度軌跡平滑,但沒有考慮速度在時間域的變化,而且實際中兩個路段節點之間的速度并非隨空間距離變化。為構造平滑連續的速度軌跡,有研究使用插值的方法基于斷面速度數據對速度軌跡進行重構,如局部加權回歸、三次樣條插值和三次Hermite 插值法等[12],但高次多項式插值近似速度軌跡的方法計算難度大,容易出現估計值震蕩和難收斂。Sun等[13]提出的分段截斷二次速度軌跡模型解決了上述高次多項式插值的問題,模型基于相鄰的三個路段節點速度構造了拉格朗日二次插值速度軌跡,但相鄰的三個路段節點速度采用出發時刻的速度,缺失考慮速度在時間域的變化,而且模型要求到達相鄰路段節點的時刻間隔足夠短,故無法應用在實際城市路段上。因此,速度軌跡重構模型有必要考慮速度在時間域和空間域的連續,從而構造近似真實的速度軌跡。
綜上所述,現有的行程時間估計模型在構造速度軌跡上,僅考慮速度在空間上或在時間上的變化,使得速度軌跡不能在時間域和空間域連續,當道路處于擁塞狀態時,估計的行程時間精度下降。本文在經典分段截斷二次速度軌跡模型的基礎上,考慮了速度在時間域的變化,提出了改進的分段截斷二次速度軌跡模型。首先,根據行程經過節點上游路段的累計時間窗來計算節點到達速度。第二,用到達路段節點時刻的速度代替出發時刻的速度,根據相鄰三個路段節點的速度構造速度軌跡。其次,基于估計的路段平均速度計算路徑的行程時間。最后,針對實際路段開展實證研究,把改進模型的估計結果和原始模型進行對比,從而評估模型的估計性能,分析試驗結果得出相關結論,為行程時間估計理論研究提供參考。
1 經典分段截斷二次速度軌跡模型改進
1.1 經典分段截斷二次速度軌跡模型
經典分段截斷二次速度軌跡模型使用三個相鄰的路段節點速度構造兩段平滑的速度軌跡,如式(1)所示。模型考慮了車輛因不同的交通狀態進行加減速的情況,以區間τ∈[AT2m-1(t),AT2m+1(t)]內歷史速度的85%最大值、最小值作為常基函數限制,如式(3)-(4)所示。
v(τ)≈v(t,x2m-1)l2m-1(τ)+v(t,x2m)l2m(τ)+v(t,x2m+1)l2m+1(τ)
(1)
其中,l2m-1(τ)、l2m(τ)和l2m+1(τ)是拉格朗日二次基函數,分別為
(2)
考慮到不同交通狀態下車輛的加減速情況,引入常基函數來構造邊界速度。邊界速度由歷史數據中同一個時段的85%的最大速度vmax和最小速度vmin確定。在τ∈[AT2m-1(t),AT2m+1(t)]時,通過相鄰的三個路段節點時間區間的速度與邊界速度值的關系可以由式(3)和(4)表示:
v[AT2m-1(t),x2m-1]l2m-1(τ)+v[AT2m(t),x2m]l2m(τ)+v[AT2m+1(t),x2m+1]l2m+1(τ)-vmax=0
(3)
v[AT2m-1(t),x2m-1]l2m-1(τ)+v[AT2m(t),x2m]l2m(τ)+v[AT2m+1(t),x2m+1]l2m+1(τ)-vmin=0
(4)
式中,xm(m=0,1,2,...M)是路徑上路段節點所在位置,M為奇數,ATm(t)(m=1,2,...,M)是車輛在t時刻出發后到達第m個路段節點的時刻;v[AT2m-1(t),x2m-1]、v[AT2m(t),x2m]和v[AT2m+1(t),x2m+1]分別是在第2m-1個、第2m個和第2m+1個這三個相鄰路段節點處的速度;插值點τ∈[AT2m-1(t),AT2m+1(t)]。
1.2 模型改進
上述經典分段截斷二次速度軌跡模型估計行程時間的隱含假設是交通流在時空間隔[AT1(t),ATM(t)]內是穩定流。為了使該假設成立,需要滿足時空間隔[AT1(t),ATM(t)]足夠短的前提,而且當路段處于擁塞的狀態時將違反該假設。由于實際中路段節點的間隔有一定距離,所以在t時刻第m個路段節點處測得的速度,不一定等于t時刻出發的車輛的速度,故構造的速度軌跡難以近似真實的車速軌跡。
在原模型基礎上,根據原模型速度軌跡表達式存在的問題,用三個相鄰路段節點到達時刻的速度v[AT2m-1(t),x2m-1]、v[AT2m(t),x2m]和v[AT2m(t),x2m]代替出發時刻測得的速度v(t,xm)、v(t,x2m)和v(t,x2m+1),得到改進的分段截斷二次速度軌跡模型,公式如(5)式所示:
v(τ)≈v[AT2m-1(t),x2m-1]l2m-1(τ)+v[AT2m(t),x2m]l2m(τ)+v[AT2m+1(t),x2m+1]l2m+1(τ)
(5)
式中,v[AT2m-1(t),x2m-1]、v[AT2m(t),x2m]和v[AT2m+1(t),x2m+1]分別是到達第2m-1個、第2m個和第2m+1個這三個相鄰路段節點的速度,其他公式變量和參數的含義同傳統的分段截斷二次速度軌跡模型。
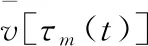
(6)
2 模型求解
本章對設計算法求解改進的分段截斷二次速度軌跡模型。首先,對相鄰三個路段節點時刻的時間間隔劃分成n個微小的時間片段,第二,判斷時間片位于對應節點的位置。其次,再根據拉格朗日二次插值基函數和常基函數用三個相鄰節點的到達時刻速度構造速度軌跡。最后估計路段的行程時間,OD節點的總行程時間是各路段的行程時間之和。模型求解的步驟具體如下:
第一步:給定每個路段節點到達的時刻ATm(t)和其對應的速度v[ATm(t),xm]。
第二步:將通過路徑節點時刻的總時間區間[AT1(t),ATM(t)]等分成n個時間間隔τ,τ=0∶n∶ATM(t)。
第三步:判斷τ的位置,用三個相鄰路段節點到達速度構造速度軌跡,計算插值τ處的函數值。
v(τ)≈v[AT2m-1(t),x2m-1]l2m-1(τ)+v[AT2m(t),x2m]l2m(τ)+v[AT2m+1(t),x2m+1]l2m+1(τ)
第四步:以歷史速度85%最大值vmax和最小值vmin為常基函數,當速度超過該值時被代替。
ifv(τ)≤vmin
v(τ)=vmin
end
ifv(τ)≥vmax
v(τ)=vmax
end
第五步:行程時間估計。
3 實例應用
3.1 數據獲取與預處理
為檢驗改進分段截斷二次速度軌跡模型的擬合度,實驗選取桂林市中山路北向南方向道路作為研究對象,全長5.2千米,雙向六車道,設計車速為60km/h。獲取數據的時間為2019年5月19日全天連續24小時,考慮到地圖數據的更新速度,速度數據采樣時間間隔為5分鐘,路段的節點共17個。節點速度首先通過拾取兩個臨近節點的上下游位置坐標,以此獲得較短的路段。其次,利用百度地圖自帶的DrivingRoute函數獲得這個路段的駕車實例。最后將返回的微小路段的速度設為近似節點的速度。采用式(7)對原始速度數據進行異常值判斷和平滑處理,當實際值與移動平均后的值偏差大于50%時視為噪聲,應該用移動平均后的值進行代替。對缺失數據采用插值法進行插補,如式(8)所示。
(7)
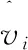
(8)
式中,t是缺失數據值對應的時刻,v(t0)是缺失數據的前一個數據,v(t1)是缺失數據的后一個數據,t0是缺失數據的前一個數據所對應的時刻,t1是缺失數據的后一個數據所對應的時刻。
3.2 誤差分析
為量化模型的擬合度,采用均方根誤差(RMSE)和平均絕對百分比誤差(MAPE)作為評價指標。改進的分段截斷二次速度軌跡模型和原模型的行程時間估計值與真實值的相對誤差結果對比如圖1所示,模型對應的綜合評價指標的對比如表1所示。在估計路徑總行程時間時,原模型的相對誤差基本保持在±15%之間,改進的分段截斷二次速度軌跡模型的相對誤差更低,基本能保持在±10%之間。改進的分段截斷二次速度軌跡模型的均方誤差和平均絕對百分比誤差比原始模型分別降低了46%和51%。
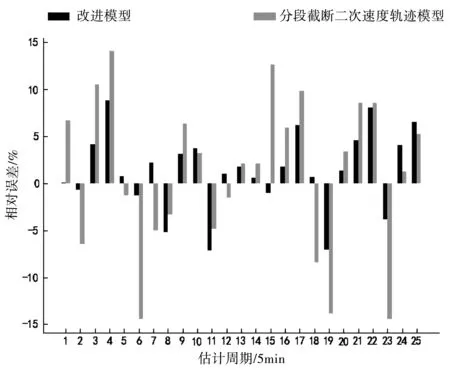
圖1 模型的相對誤差對比

表1 模型估計誤差指標比較
3.3 結果分析
①如圖2所示,當處于8∶00-9∶00時段(出行的高峰時段)時,研究道路的行程時間受交通狀態的影響而波動。改進的分段截斷二次速度軌跡模型估計的行程時間與原模型相比能更好地擬合真實行程時間,說明用節點到達時刻速度構造速度軌跡突破了原模型的局限性,能適應擁堵條件下的行程時間估計。
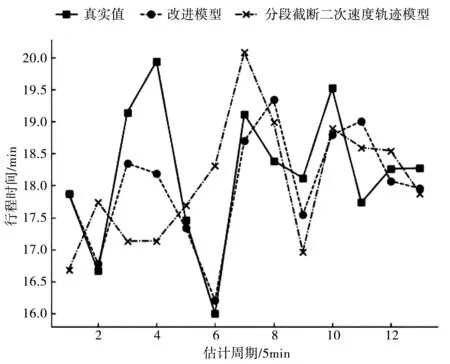
圖2 8∶00-9∶00模型結果對比
②如圖3所示,當處于非出行高峰時段(9∶05-10∶00),原模型比改進的分段截斷二次速度軌跡模型更容易出現高估的情況,改進的分段截斷二次速度軌跡模型與真實數據比較表現出良好的一致性。

圖3 9∶05-10∶00模型結果對比
綜上所述,改進的分段截斷二次速度軌跡模型估計結果與真實行程時間擬合較好,且估計結果與真實行程時間隨時間的變化趨勢一致。改進的分段截斷二次速度軌跡模型對交通狀態的變化反應更靈敏。說明改進的估計模型能準確根據行程中的交通狀態及時調整估計的行程時間,使其接近道路真實交通狀況下的行程時間。
4 結論
本文在經典分段截斷二次速度軌跡模型的基礎上,考慮了行程中的速度變化,提出了一種改進的分段截斷二次速度軌跡模型。首先,根據行程經過節點上游路段的累計時間窗來計算節點到達速度。其次,用到達路段節點時刻的速度代替出發時刻的速度,并用相鄰的三個路段節點的到達速度構造速度軌跡,引入常基函數構造邊界速度作為限制。最后,基于路段的平均速度估計行程時間。針對實際道路開展實證研究,試驗結果表明:(1)改進的分段截斷二次速度軌跡模型比原模型在均方誤差和平均絕對百分比誤差上分別降低了46%和51%。(2)當處于出行高峰時期,改進的分段截斷二次速度軌跡模型與原始模型相比提高了擬合度。證明了改進后的模型能適應擁堵的交通狀態,突破了原始模型的局限性。(3)改進的分段截斷二次速度軌跡模型對原模型高估或低估的問題有顯著的改進,對交通狀態變化的反應更靈敏。
本文用改進的分段截斷二次速度軌跡模型估計行程時間,模型不涉及利用歷史數據進行短時的預測。如何利用歷史和當前的節點速度實現行程時間的實時估計,在后續研究中需要進一步完善。

