基于深度強化學習的車輛路徑問題求解方法

黃 琰，張 錦,2,3

（1.西南交通大學，交通運輸與物流學院，成都 611756；2.綜合交通運輸智能化國家地方聯合工程實驗室，成都 611756；3.綜合交通大數據應用技術國家工程實驗室，成都 611756）

0 引 言

車輛路徑問題（Vehicle Routing Problem，VRP）于1959 年由Dantzig 和Ramser[1]提出并用于解決卡車調度問題，后被Lenstra 和Kan[2]證明是一種NP-hard 問題。作為交通運輸與物流領域最為經典的組合運籌優化問題，VRP 歷經幾十年的研究和討論而經久不衰。

基于現實情況，學者們將相關的約束條件添加到標準的VRP 中，設計了多種對應的VRP 擴展問題。如帶時間窗的車輛路徑問題（Vehicle Routing Problems with Time Windows, VRPTW）、隨機服務的車輛路徑問題（Vehicle Routing Problem with Stochastic Travel and Service Time and Time Windows, VRPSTSTW）[3]、電動汽車車輛路徑問題[4-5]（Electric Vehicle Routing Problem,EVRP）、考慮增加車場數量的多車場車輛路徑問題[6]（Multidepot Vehicle Routing Problem, MDVRP）、帶時間窗和人力分配的車輛路徑問題[7]（Manpower Allocation and Vehicle Routing Problem with Time Windows, MAVRPTW）、考慮一致性約束的車輛路徑問 題[8]（Consistent Vehicle Routing Problem, Con-VRP）等，并被廣泛應用于物流配送、醫療服務[7]以及消防、潛探、巡檢等特殊領域。較為常見的車輛路徑問題的應用場景、特征和相關經典文獻詳見文獻[9]。

車輛路徑問題的常規求解方法主要有精確算法、經典啟發式算法和元啟發式算法[9-10]。目前，車輛路徑問題的傳統求解方法均能不同程度地適應各類型的車輛路徑問題，但傳統求解方法通常針對具體模型和部分靜態進行建模和求解，并不具備自主學習和決策的能力。

深度強化學習是一種能夠實現從原始輸入到輸出直接控制的人工智能方法[11]，設計的方法無需人工設計或推理，使得其自主解決車輛路徑問題，甚至未來自主改進至優于傳統方法變得可能。在現代物流快速發展的基礎上，面對復雜、數據規模較大的車輛路徑規劃情景，應當設計可信演化能力更強、算法柔性更大的人工智能方法，以適配實際的車輛路徑問題場景，有效支撐智慧物流的發展。

常見的深度強化學習方法包括深度Q 網絡方法（Deep Q-learning Networks, DQN）、演員-評論家方法（Actor-Critic,AC）、深度確定性策略梯度方法（Deep Deterministic Policy Gradient, DDPG）、近端策略梯度優化方法（Proximal Policy Optimization，PPO）等。目前，深度強化學習在VRP 中的應用是研究的熱點之一[10]，相關研究主要集中在采用逐一插入節點的方式構造解的“端到端”深度強化學習方法和運用深度強化學習方法設計啟發式算法兩個方向。相關文獻運用方法及主要成果整理如表1所示。

表1 深度強化學習方法在車輛路徑問題中的應用Tab.1 Application of deep reinforcement learning to vehicle routing problems

一方面，相關學者通過逐一插入節點的方式設計“端到端”輸出解的車輛路徑問題的深度強化學習方法。Nazari 等[12]受到TSP 旅行商問題的深度強化學習相關研究的啟示，結合車輛路徑問題的特性，通過改進指針網絡PtrNet 的編碼器，設計了適用于VRP 問題的深度強化學習方法。KOOL等[13]提出了AM 方法，引入注意力機制Attention并設定探索基線Rollout Baseline 用于修正強化學習的獎勵。Vera 等[14]基于深度強化學習在多智能體協作系統中的應用，提出了解決固定車隊規模的多車輛路徑問題的深度強化學習方法，相比啟發式方法得到了較優的實驗結果。Peng 等[15]在AM方法的基礎上引入動態注意力機制，相比文獻[13]將算法效率提升了20～40 倍。Bdeir 等[16]針對VRP設計編碼器并與DQN思想結合設計了RP-DQN方法，并證明在客戶數量為20、50、100 的CVRP(Capacitated Vehicle Routing Problem)上優化效果均優于文獻[12]和文獻[13]。ORENJ 等[17]提出運用圖神經網絡表示VRP 的環境狀態，并設計了一種在線-離線學習相結合的方法。韓巖峰[18]提出了基于注意力機制和AC 算法框架的深度強化學習方法，并用于解決帶時間窗的無人物流車隊配送問題。

另一個研究方向則是運用深度強化學習方法針對特定車輛路徑問題設計啟發式算法。Chen[19]等將車輛路徑問題定義為序列到序列的問題，并運用指針網絡結合AC 方法設計啟發式算法NeuRewriter，并在實驗結果上優于文獻[12]和[13]。LU 等[20]通過定義改進算子和干擾算子并結合深度強化學習方法構建了啟發式算法L2I，首次在實驗結果上超過了專業求解器LKH3[21]。之后，Wu 等[22]運用自注意力機制結合REINFORCE 構建了啟發式算法，通過對歷史解決方案離線學習取得了較好的實驗結果。Falkner 等[23]運用深度強化學習方法改進多個并行解決方案，設計了啟發式算法JAMPR，并應用于CVRP 問題和VRPTW 問題。馮勤炳[24]設計了基于DQN的強化學習超啟發算法，實驗證明對比傳統方法有效減少了總成本，提升了算法魯棒性。Zhao 等[25]通過將深度強化學習方法與局部搜索算法相結合設計了啟發式算法，實驗結果較好，并將求解效率提升了5～40 倍。Gao 等[26]在大規模領域搜索算法框架下結合圖注意力神經網絡GAT 和PPO 構建了啟發式算法，將問題解決規模擴大至400個客戶服務點。

綜上，運用深度強化學習方法設計啟發式算法求解車輛路徑問題可以有效地提升求解的速度和效果，但該類模型較適用于求解固定環境和類型的車輛路徑問題。部分學者嘗試離線學習實例數據求解車輛路徑問題，該類實驗效果較好，但需要大量數據和算例作為輸入，一定程度上影響了算法的效率，降低了方法的實用性。許多學者致力于研究“端到端”的車輛路徑問題求解方法，該類方法能夠較好地針對不同約束條件的車輛路徑問題，但通常需要通過波束搜索、局部搜索等方式提升直接輸出解的質量。Bdeir[16]等提出的RPDQN 方法，實驗結果在現有“端到端”方法中表現較優，但由于DQN 方法的動作選擇方式，尚存在值函數過估計、探索局限等問題，該問題將在后文詳細說明并改進。同時，并未有學者系統性地對車輛路徑問題強化學習決策過程進行詳細設計。

本文針對CVRP 設計了“端到端”輸出解的車輛路徑問題的深度強化學習方法，其主要貢獻如下：

（1）提出了一種基于上置信區間算法（Upper Confidence Bound Apply to Tree,UCT）改進策略選擇的DQN 方法，通過平衡智能體對策略的利用與探索，解決現行方法探索局限的問題，提升方法的效果。

（2）針對CVRP，系統性地設計了車輛路徑問題場景下的強化學習決策過程，并設計了車輛路徑問題場景下的狀態-動作空間、獎勵函數、策略選擇方式等決策過程要素。

1 問題與目標

1.1 問題描述

CVRP 即對每一個服務的車輛都有裝載能力約束的車輛路徑問題，由一組W輛具有裝載能力為cw的車輛，對一系列分布在地理上不同位置的L個顧客進行服務，每個需求點只能由一輛車服務且每個車輛的路線開始于車場，完成服務后回到車場。

1.2 優化目標

深度強化學習是通過環境與智能體的不斷交互，修正不同狀態下的動作選擇，最終輸出一系列較優動作的過程。為了達到最終期望的結果，需要通過設置一個優化目標來更好地引導智能體。

參考本文研究的CVRP 傳統模型中的目標函數設定優化目標：在滿足車輛裝載約束的基礎上，考慮車輛行駛距離總和最短，如下所示：

2 傳統深度Q網絡方法

深度Q 網絡[27-28]是在Q-learning 的基礎上，構建一個參數為Φ的深度神經網絡代替Q-learning的Q值表，并通過智能體與環境不斷交互更新函數參數，使得函數Q?(s,a)可以逼近現實的狀態動作值函數Qπ(s,a)，該過程為：

式中：s′為下一個狀態s′的向量表示；a′為下一個動作a′的向量表示。

函數Q?(s,a)與Qπ(s,a)之間的誤差，可表示為損失函數：

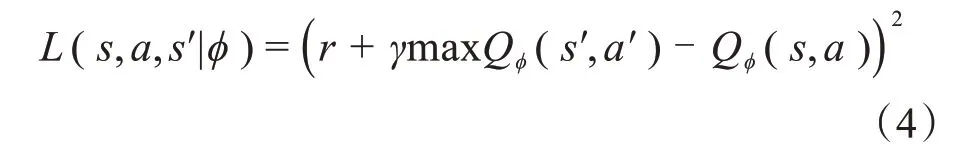
函數Q?(s,a)逼近Qπ(s,a)的過程就是損失函數不斷梯度下降的過程。

2.1 值函數網絡設計

本文參考Kool等[13]設計的基于Transformer框架的注意力模型以及Bdeir等[16]提出的RP-DQN方法，設計了值函數網絡。網絡結構為基于Transformer 框架的注意力網絡，主要組件包括輸入層、解碼器、編碼器和輸出層。

值函數網絡整體結構如圖1所示，具體細節詳見文獻[13]和[16]。

圖1 深度Q網絡值函數網絡結構示意圖Fig.1 Structure of value function network of Deep Q-learning Networks

這些節點嵌入通過N個串聯的注意力模塊（Attention Blocks,AB）進行傳導和更新，每個注意力模塊由一個多頭自注意力層（Multi-Head Self-Attention Layer, MHA）和一個全連接的前饋層（Feedforward Layer, FF）組成，激活函數為ReLU函數，每層MHA 與FF 之間通過殘差連接和批量歸一化處理（Batch Normalization, BN）連接而成，并允許信息傳遞時跳過連接。

2.1.2 解碼器

解碼器由1個MHA 和1個單頭注意力層（Single-Head Attention,SHA）組成。

解碼器每一時刻t的輸入是當前時刻由編碼

式中：u0為選擇訪問車場輸出的q值；ui為選擇訪問節點i輸出的q值；w?i,t為t時刻節點i的剩余需求；c?t為t時刻節點i的車輛的剩余裝載量。

其中，式（8）表示車場不允許被連續訪問；式（9）表示需求大于車輛剩余裝載的節點和已被服務過的節點（剩余需求為0）不允許被訪問。掩碼M的規則設定能夠很好地反映VRP 問題的約束條件。本文僅針對CVRP設計了掩碼的規則，相關學者可通過增加掩碼M規則將該方法拓展至各類車輛路徑問題。

式中：dk為維度系數，用于平衡各節點之間的數量級，通常取64；W k和W q分別表示節點狀態特征和節點嵌入權重向量。

2.2 車輛路徑問題的決策過程

深度強化學習的決策過程為馬爾科夫決策過程（Markov Decision Process，MDP）具有馬爾科夫性，即一個隨機過程其未來狀態的條件概率分布僅依賴于當前狀態，與之前任意時刻無關。在CVRP問題中，可將求解的過程視作車輛在某時刻與環境進行交互的過程，這個過程是一個離散動作空間。在僅考慮統一車型且不考慮時間窗的情況下，模型中w輛車可視為一輛車取貨w次的過程，雖然該過程的每一個決策之間并不存在實際的時間順序，但決策過程依舊僅依賴當前的狀態，具有馬爾科夫性，故這個過程可以視為半馬爾科夫決策過程。

在這個虛擬的過程中，存在一個智能體即車輛，車輛從起點出發選擇一個動作a1，由外部環境給予一個即時的獎勵r，同時環境根據動作更改成狀態s1，這個過程不斷交互，直到所有顧客服務完畢，此時返回所有獎勵的和。

智能體與環境交互做出動作的最終目標是達到期望累計獎勵最大，可以表示為：

2.2.2 獎勵函數

獎勵函數的設定直接決定了強化學習方法的收斂性和優化方向，結合CVRP問題的相關約束條件以及式（1）關于本文優化目標的定義，本文定義了智能體每次做出決策，環境給予該決策對應顧客之間距離倒數的正獎勵如下所示：

式中：rt表示t時刻的獎勵。

3 基于UCT改進的DQN

3.1 傳統DQN的問題

深度Q 網絡存在對于Q 值過估計的問題。由公式（2）可知，DQN網絡訓練過程是通過近似估計一個函數逼近現實的狀態動作值函數的過程。由于初始狀態未知以及原始參數的設定，會導致這個過程的開始對于函數的估計產生偏差。而由于深度Q 網絡選擇執行的是Q 估計值最大的動作，因此過高估計的動作被選擇的概率較大；深度Q網絡目標網絡凍結的機制，也會導致其不斷放大值的過大估計，導致最終結果出現偏差。

同時，由于DQN 選擇執行的是Q 估計值最大的動作，智能體每次進行交互的軌跡是一致的，對于未選擇動作的探索程度較小，僅是對已經確定的策略進行利用，而非對環境進行探索，難以覆蓋所有的狀態和動作。若單純使用深度Q 網絡會導致陷入局部最優，不利于最優策略的選取，方法的收斂性和穩定性較差。

3.2 方法改進

本文通過結合UCT 算法改進DQN 中的動作選擇方式以改進DQN的過估計和探索局限問題。

UCT 算法是蒙特卡洛樹搜索算法（MCTS）的一個拓展，MCTS 作為一種經典啟發式搜索算法，最早由Kocsis 等[29]在2006 年提出，UCT 算法是在MCTS 的基礎上，將上置信區間UCB 值引入MCTS用于算法決策值的計算，被廣泛應用于搜索空間較大的決策過程或象棋、圍棋游戲的AI 程序中，如Alpha Go等。

強化學習的本質是通過不斷探索環境并充分利用探索的經驗進行控制與決策的過程[30]。傳統DQN方法在解決環境的探索與利用平衡問題時是通過ε-greedy策略，通過調整貪婪和隨機的概率對環境進行充分探索。

但由于ε-greedy策略是隨機無向的探索，在小規模的簡單問題中尚能進行。但面對較為復雜的問題，特別是VRP問題，要求每個節點顧客必須得到服務，因此對每個節點的特征進行探索是必要的。這種隨機無向的探索數據利用率較低，難以保證在短時間內對所有節點特征進行探索。UCT算法則很好地解決了這個問題，UCT 算法定義了一個上置信區間值UCB為：

具體到本文的改進，是將DQN 算法中智能體做動作選擇時選擇輸出最大q值動作的策略，改為選取k個較大q值的節點并向下遍歷計算其葉節點的qUCB值，輸出qUCB值最大的節點動作。值得一提的是q值的輸出借鑒了Hasselt[31]等設計的DQN改進方法，為Q 估計與Q 現實中較小的數值，以此可以減少DQN 的過估計問題。動作a的qUCB值可表示為qUCB(a)，表達式如下：

改進后的方法流程如圖2所示，細節及具體描述如下。

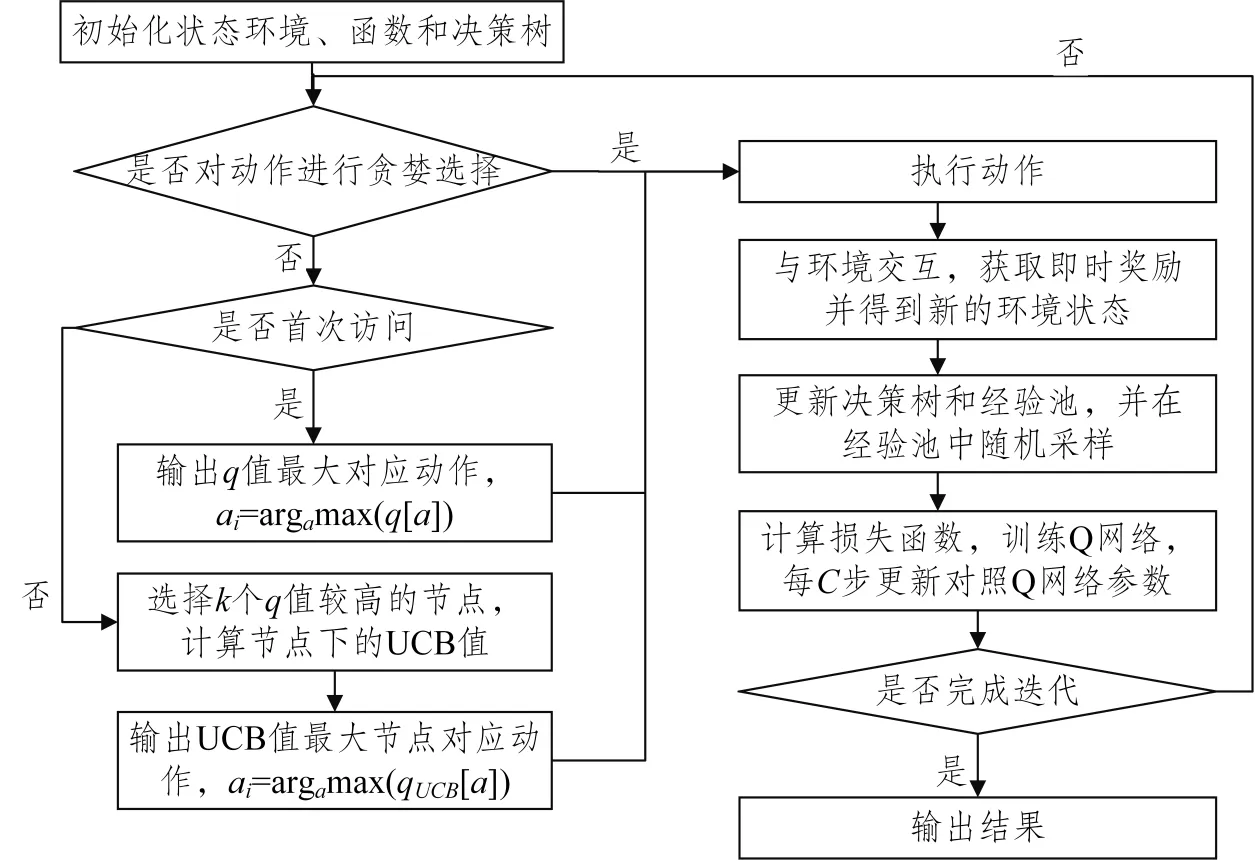
圖2 基于UCT改進動作選擇的DQN方法流程圖Fig.2 Flow diagram of DQN method for improved policy decision-making based on UCT

步驟1 初始化虛擬狀態環境。

步驟2 初始化經驗池、動作價值函數Q 網絡、對照動作價值函數Q 網絡、決策樹估計函數；設定參數：經驗池容量N、最大訓練迭代步數M、折扣率γ、學習率α、Adam 函數參數β1 和β2、Q 網絡參數Φ、對照Q 網絡參數Φ′、更新間隔C、貪婪概率ε、修剪參數k、狀態訪問次數ns、動作狀態訪問次數nsa。

步驟3 有ε概率輸出隨機動作；否則，判斷是否首次訪問節點，即ns(s)=0。若是，則輸出當前q值最高動作，ai=argamax(q[a])；若不是，則輸出k個節點中qUCB值最大的動作，ai=argamax(qUCB[a])。

步驟4 執行步驟3中選擇的動作，環境依據動作給予式（5）和式（6）的即時獎勵ri，并更新得到新的環境狀態xi+1。

步驟5 更新經驗池和決策樹。當經驗池飽和時，從經驗池的最底端進行新的數據替換。

步驟6 從經驗池中隨機采樣并代入式（9）計算損失函數梯度下降訓練Q網絡，每隔C步更新對照Q網絡參數。

步驟7 判斷是否符合訓練終止條件，進入步驟8；否則，返回步驟3。

步驟8 輸出結果。

改進的DQN框架示意圖詳見圖3。

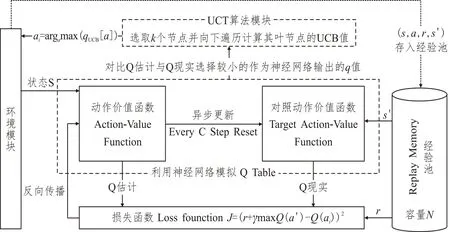
圖3 基于UCT改進動作選擇的DQN框架示意圖Fig.3 Framework schematic diagram of DQN method for improved policy decision-making based on UCT

4 實驗分析

4.1 實驗參數敏感度分析和選擇

本文選取的實驗參數敏感度測試數據集來自Augerat[32]1995 年提出的Set A 數據測試集中的An32-k5 號數據集。該數據集共有31 個需求點、載具裝載限制為100、載具數量限制為5 輛，車場坐標、服務點坐標和需求量如表2 所示，其中序號1為起終點，其余為需求點。

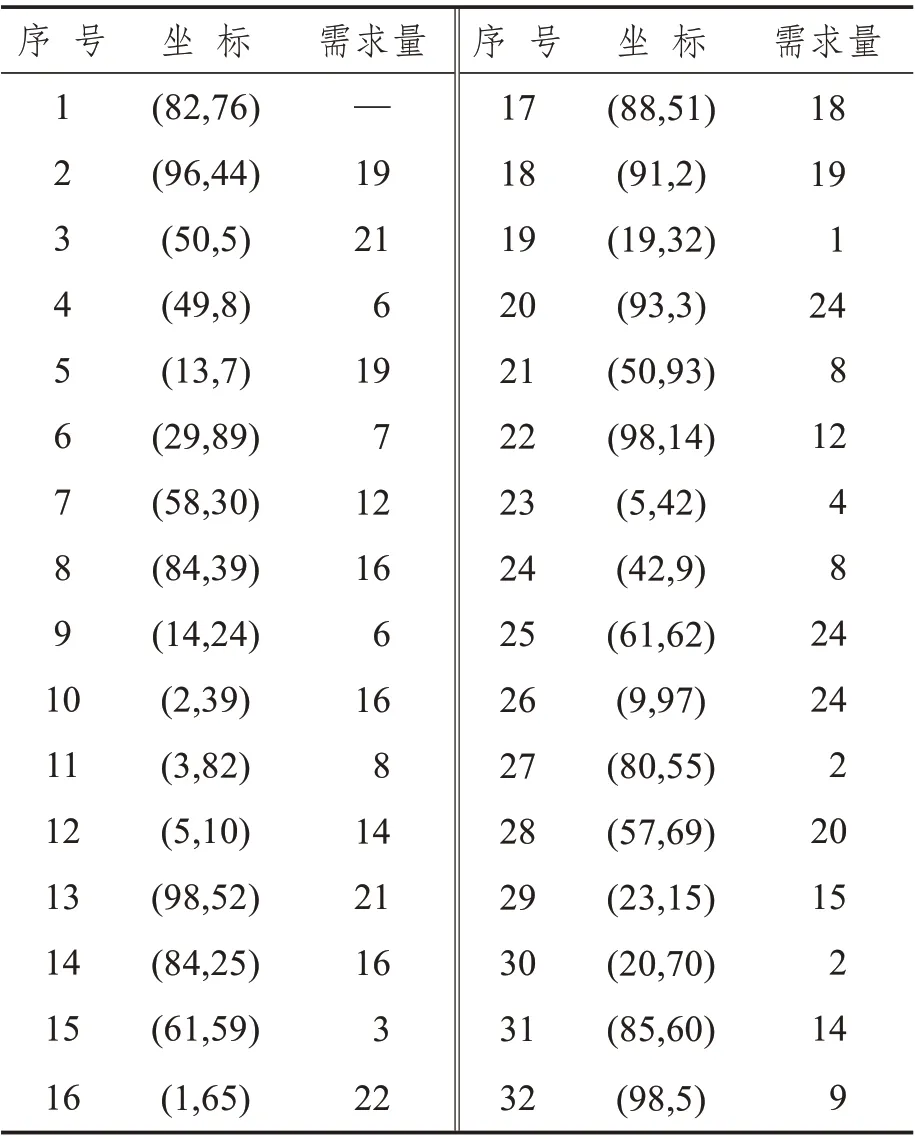
表2 實驗參數敏感度測試環境信息Tab.2 Environmental information for sensitivity testing of experimental parameters

依據上述數據，本文在gym 中創建了一個100*100 的網格作為本文方法參數敏感性實驗的虛擬環境，將數據集數據映射到虛擬環境中。

為測試本文方法在不同參數下的表現以便選擇較優的參數進行最終的實例求解，本文對深度Q網絡中敏感度較高、能夠顯著影響訓練效果的參數（經驗池容量N、UCT 修剪數、對照動作價值網絡更新間隔C、折扣率γ和學習率α）進行敏感性分析。其中，經驗池容量N、UCT 修剪數、對照動作價值網絡更新間隔C并未對算法收斂和累計獎勵結果變化造成顯著的影響，因此本文對變化較為顯著的折扣率γ和學習率α進行詳細分析。

為更好地展示算法訓練效果和變化情況，本文通過把每100 個訓練匯合所得獎勵求平均的方式將10 000 次迭代等效處理為100 個趨勢點用于累計獎勵變化趨勢圖的繪制。

4.1.1 折扣率的分析與選擇

在其他參數不變的情況下，分別對折扣率γ取0.7、0.9 和0.99 的情況進行模擬，迭代10 000 次后累計獎勵值變化趨勢如圖4所示。

圖4 不同折扣率下累計獎勵隨迭代次數變化情況示意圖Fig.4 Variation in rewards with number of iterations under different γ

由圖4 可得，折扣率γ的調整顯著影響了累計獎勵的變化與收斂情況。γ取較大值0.99 時，由于對以往經驗過于關注，導致最終累計獎勵值未能更好地趨近最優值；而當γ為0.7 時，過小的折扣率導致未能很好地學習過去較好的動作選擇，最終未在設定迭代步數內完成收斂。

4.1.2 學習率的分析與選擇

在其他參數不變的情況下，分別對學習率α取0.005、0.05 和0.001 的情況進行模擬，迭代10 000次后累計獎勵值變化趨勢如圖5所示。

圖5 不同學習率下累計獎勵隨迭代次數變化情況示意圖Fig.5 Variation in rewards with number of iterations under different α

由圖5 看出，學習率α的調整影響了累計獎勵的收斂速度和穩定性。α取0.05 和0.005 時，由于學習率過大導致較快出現收斂趨勢，但未能學習到最優策略導致后續逐步出現震蕩；當α取值為0.001時，累計獎勵平穩上升并有較好的收斂性。

4.2 實驗環境設置

為了更好地與其他深度強化學習方法進行對比，本文在文獻[12]定義的車輛路徑問題環境下進行實驗，該環境自提出以來被用于測試國內外各類深度強化學習方法[12-20,22,23,25,26]在車輛路徑問題場景下的性能。實驗假設節點位置和需求是從固定分布隨機生成的，具體來說，客戶和車場位置是從1×1的單位方格中隨機生成的，每個節點的需求在[0,10]中隨機選擇。此處為模擬真實需求，遵循了文獻[13]的設定將需求值定義為離散的正整數。針對智能體行為設置，本文假設車輛在時間0時位于車場，在每次交互過程中，車輛從客戶節點或倉庫中進行選擇，以便下一步訪問，直至所有節點訪問結束，返回車場。

本文將分別對比20、50、100 三個問題規模下的CVRP 問題，以下分別簡稱為CVRP-20、CVRP-50 和CVRP-100，相應規模下的額定載重分別為30、40 和50。通過在每個數據規模下隨機生成1 000個實例，并且每個實例只使用一次，通過計算平均成本對比實驗結果。

基于上述實驗設置本文在Intel(R) Core(TM)i7-4720HQCPU@2.60 GHz、RAM 16.0 GB電腦上使用Python 語言，采用Tensorflow 框架在Jupyter Notebook中實現設計的基于UCT改進動作選擇的DQN 算法。在參數敏感性分析的基礎上，實驗參數設置如表3所示。

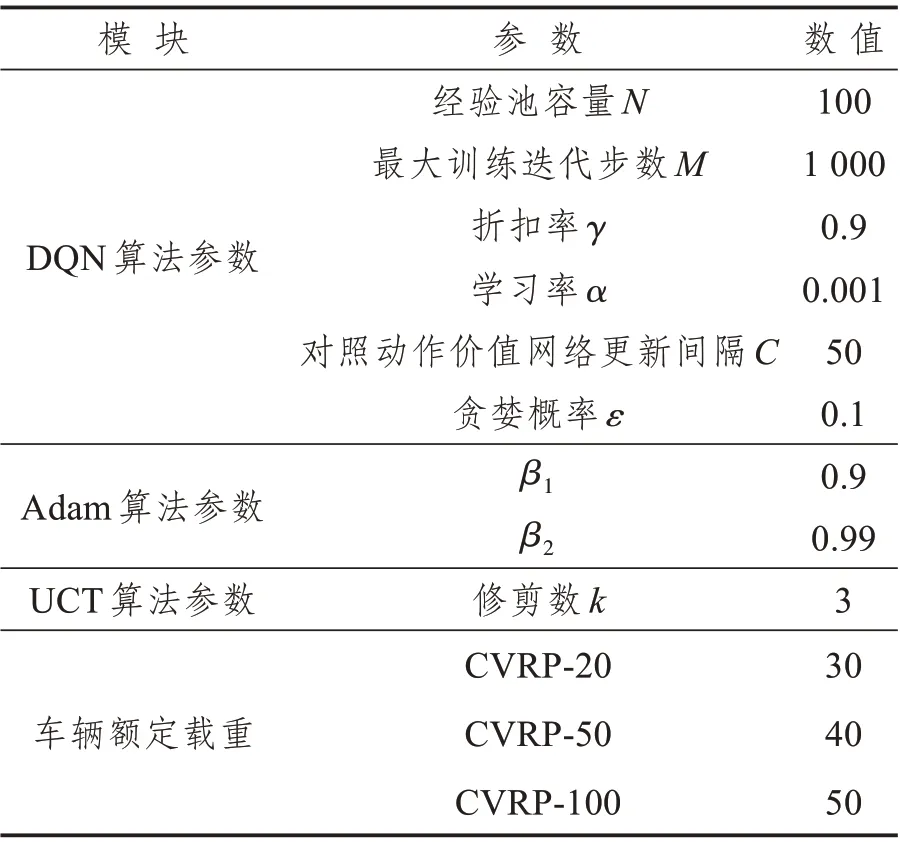
表3 實驗參數設置Tab.3 Experimental parameter settings

4.3 方法有效性分析

為反映UCT-DQN 的學習過程和收斂情況并直觀地與RP-DQN[16]進行對比，本文將各數據規模上兩種方法的獎勵及優化目標變化情況進行了繪制，如圖6所示。其中，優化目標依據公式（1）為車輛行駛總距離的成本，成本越低，實驗效果越優。同時，為加強實驗結果的可讀性，本文通過每20步取平均值的方式對獎勵和優化目標值進行了平滑處理。

由圖6可以看出，兩者都是標準的深度強化學習曲線。智能體獲取的獎勵值曲線波動上升，說明智能體根據學習情況，逐步調整動作選擇策略。訓練初期由于Q值的估計準確性較低導致曲線波動較大，隨著訓練次數的增加，逐步學習到了較好的策略，波動逐步趨于穩定，說明兩種深度強化學習方法均具有較好的收斂性和準確性。

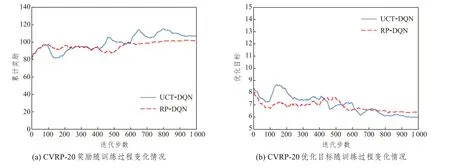
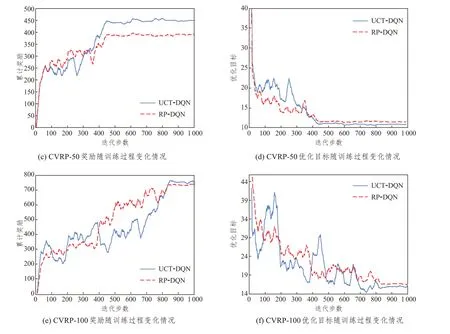
圖6 各規模環境獎勵及優化目標隨訓練過程變化情況示意圖Fig.6 Variation in rewards and optimization objectives with training process in various environments

對比兩種方法，在CVRP-20 中，由于實驗規模較小，兩種方法均較快地探索到較好的解決方案，并 很 快 收 斂；在CVRP-50 和CVRP-100 中，RPDQN 方法雖較快呈現出收斂趨勢，但由于探索局限和過估計問題，過分依賴已探索的動作策略，導致最終收斂的值尚有一定的提升空間。本文的UCT-DQN 方法，雖收斂趨勢較為緩慢，但在三個問題規模中最終都獲得了較高的獎勵和較低的成本。通過統計分析，本文方法在CVRP-20、CVRP-50 和CVRP-100 三個規模中的平均成本分別為6.24、10.80 和16.23，對比RP-DQN 方法分別提升了1.89%、1.10% 和2.17%，取得了較好的實驗結果。

本文所提方法對比RP-DQN 方法雖收斂時間較長，但實際應用環境下，依托GPU 服務器、高性能計算機或超算平臺等，本文的方法可以快速輸出較高質量的可行解或作為優秀的初始解用于啟發式算法、求解器等。

將本文方法所得結果進一步與專業求解器OR Tools、Gurobi、LKH3、啟發式算法節約里程法CW、掃描算法SW 以及其他“端到端”的深度強化學習方法結果進行對比，結果整理如表4所示。其中，本文以每個數據規模下的最優結果為基線，對比其他方法和求解器與其的成本偏差，偏差率值越小，方法所得結果越優。

由表4 可以看出，本文所提方法在CVRP-20中平均成本僅高于求解器Gurbi、LKH3 以及文獻[17]的SOLO 的在線學習方法，與上述三種方法相比，本方法的耗時較短，能夠一定程度上提升運算效率；在CVRP-50 問題中，實驗結果略遜于LKH3以及文獻[15]的AM-D方法；在CVRP-100問題中，實驗結果相比LKH3 求解器有3.71%的成本誤差，但優于其他所有“端到端”的深度強化學習和啟發式算法。實驗結果顯示，在充分訓練的基礎上，隨著問題規模的擴大，本文所提方法性能優勢逐步顯示，且相比LKH3 求解器雖有較小誤差，但能較好地提升求解效率，說明該方法有較好的應用前景。

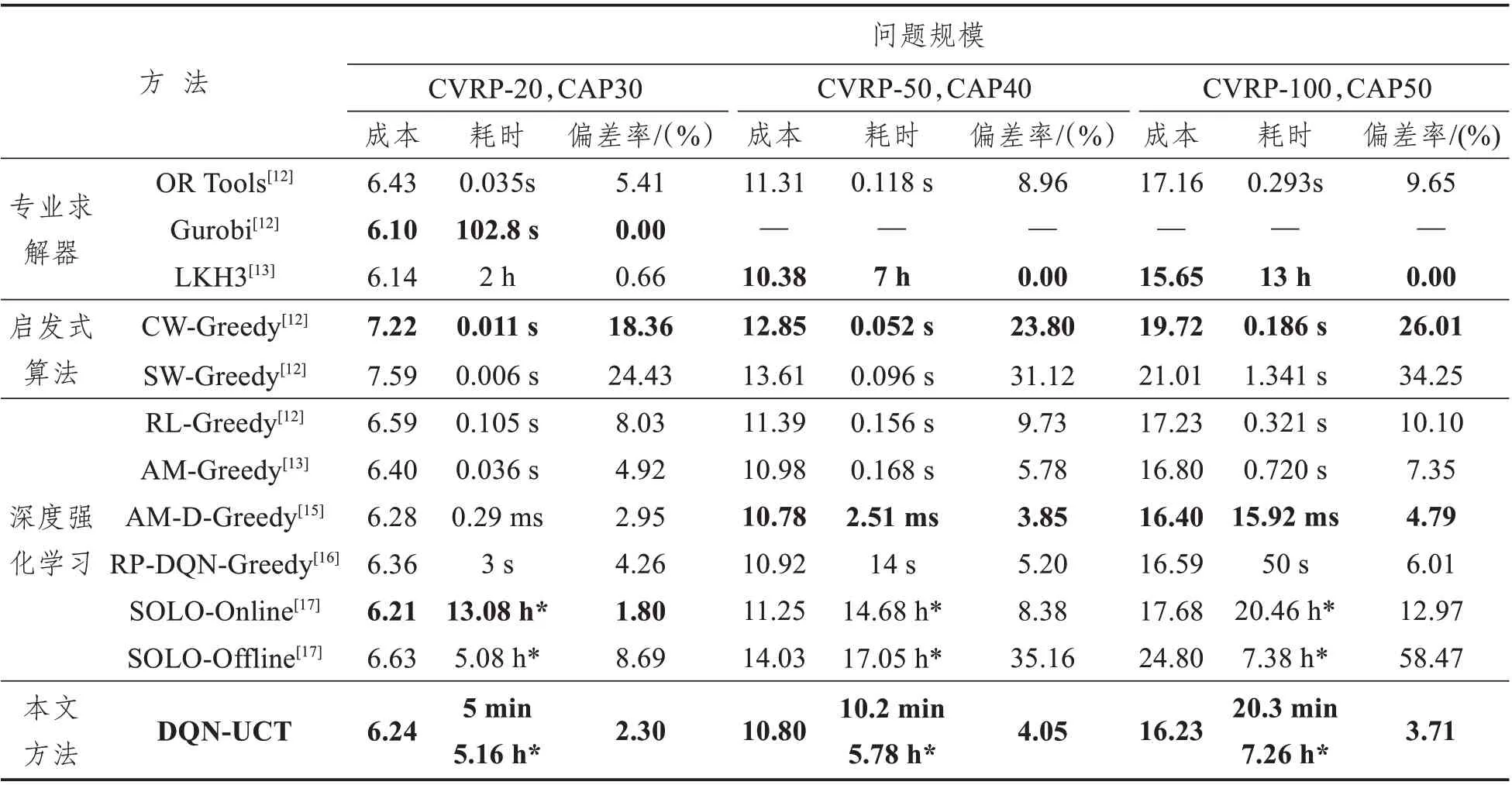
表4 實驗結果對比Tab.4 Comparison of experimental results

5 結束語

本文提出一種基于UCT算法改進動作選擇方式的DQN 方法。所提出的深度強化學習方法用于車輛路徑規劃場景，通過智能體與虛擬環境交互獲得獎勵尋求行駛距離最短的動作組合策略，“端到端”解決了考慮車輛裝載限制約束的車輛路徑問題。實驗結果表明，本方法能夠得出與專業求解器質量相當的解。所提算法在充分訓練的基礎上，能切實提高車輛路徑問題的求解效率，未來在實際應用領域更具可行性。下一步工作，將考慮群智感知環境下DQN 的可信演化問題，結合企業實際進一步驗證模型的場景實用性；同時，將本文方法運用在其他約束條件或更大規模的車輛路徑問題也是本文的下一步工作之一。