分步突破精準切入 策略總結典例探究
——以一道函數與幾何綜合題為例
?江蘇省蘇州高新區實驗初級中學 張 玲
1 考題呈現
考題(2021年江蘇無錫市中考卷第27題)在平面直角坐標系中,點O為坐標原點,直線y=-x+3與x軸交于點B,與y軸交于點C,二次函數y=ax2+2x+c的圖象過B和C兩點,且與x軸交于另一點A,點M為線段OB上的一個動點,過點M作直線l平行于y軸交BC于點F,交二次函數y=ax2+2x+c的圖象于點E.
(1)求該二次函數的表達式;
(2)當以C,E,F為頂點的三角形與△ABC相似時,求線段EF的長度;
(3)已知點N是y軸上的點,若點N,F關于直線EC對稱,試求點N的坐標.
2 分步突破
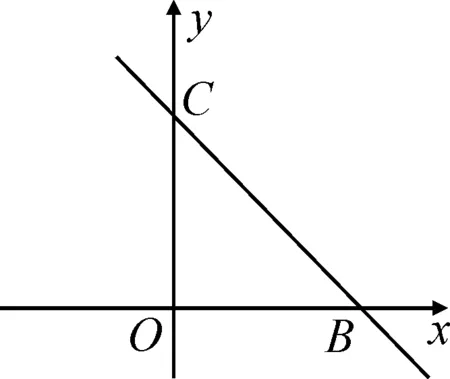
圖1
本題目為函數綜合題,以拋物線與直線為背景,依托坐標系中的點構建三角形,所設三問全面考查學生的基礎知識和綜合能力.第(1)問求函數的解析式,考查待定系數法;第(2)問由三角形相似,考查函數中的相似構建;第(3)問則是關于點的對稱,考查對稱轉化.下面結合具體函數的圖象,分步突破.
2.1 第一步——待定系數法求解
二次函數y=ax2+2x+c中需求a和c的值,只需求拋物線上點B和C的坐標即可.由于兩點是直線y=-x+3與坐標軸的交點,故可直接求得.
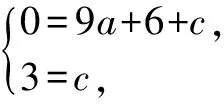
2.2 第二步——構建相似模型
該問探究以C,E,F為頂點的三角形與△ABC相似,需要關注問題中的兩點:①題干沒有給定相似對應關系,需要分類討論;②關注兩三角形的角度關系.

圖2
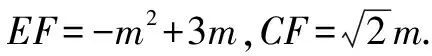
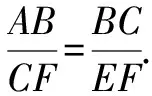
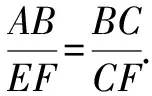

2.3 第三步——對稱轉化推理
第(3)問是函數背景下的幾何對稱問題.求對稱點N的坐標,有兩點要求:(1)點N位于y軸上,則其橫坐標的值為0;(2)點N和F關于直線EC對稱,則它們到直線EC的距離相等,可依托該特性構建幾何關系.
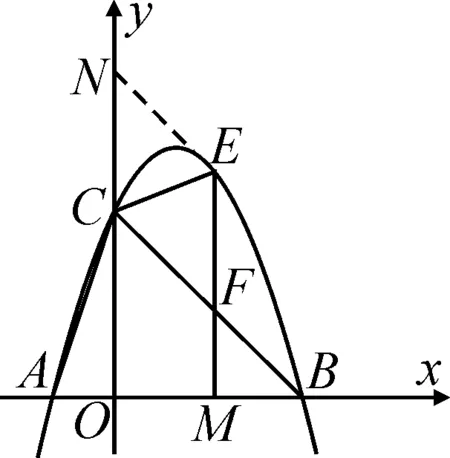
圖3
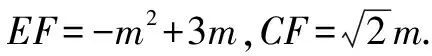
3 解法探究
上文對一道拋物線綜合題進行了分步突破,分別求解函數的解析式,探討三角形相似關系,分析點的對稱.從本質上看,考題為函數與幾何綜合題,掌握函數背景中幾何圖形的探究方法是解題的關鍵.下面對問題解法進行深入探究.
3.1 函數背景下的三角形相似
上述考題第(2)問探究三角形的相似問題,有兩大特點:一是沒有設定對應關系,二是兩三角形含有特殊對應角(45°角).故需要討論三角形的相似對應,且只需求兩種情形.通常對于函數背景下的三角形相似問題,可以采用如下策略,分三步論證.
第一步,假設結論成立,分情形討論.
對于沒有明確對應關系的相似三角形問題,可先設定分類標準,再分析所涉三角形是否含有特殊對應角.若有,則提取對應角,再分類;若沒有,則分別討論三種對應情形.
第二步,設未知,求線段或邊長.
對于三角形相似問題,可從角度和邊長對應成比例兩個視角突破,但在函數背景下,采用邊長對應成比例更容易構建等式.解析時,可設定關鍵點的坐標,推導相關線段或邊長.
第三步,建方程,精計算.
根據相似三角形對應關系列比例式,將比例式中的線段用含點的坐標參數的線段替換,進而構建含有坐標參數的方程,通過解方程精準求解.
基于上述解題策略,下面對例1進行進一步探究.
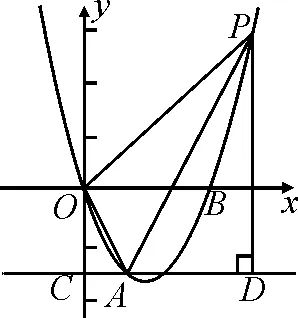
圖4
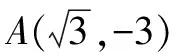
(1)求該拋物線的解析式;
(2)在拋物線上取一點P,過點P作直線AC的垂線,設垂足為點D,連接OA,使以點A,D,P為頂點的三角形與△AOC相似,試求出對應點P的坐標.
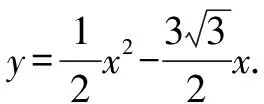
(2)因為△AOC為直角三角形,故以A,D,P為頂點的三角形也必須為直角三角形.故點C始終對應點D,只有△OCA∽△ADP和△OCA∽△PDA兩種情形.同時需要分點P位于直線AD上方和下方兩種情形.
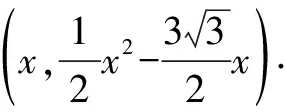
①若點P在直線AD上方,則
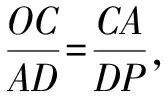

當點P(0,0)時,也滿足△OCA∽△PDA.
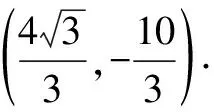

3.2 函數背景下的點對稱
上述考題的第(3)問求兩點關于直線對稱時其中一點的坐標,屬于函數背景下的點對稱求坐標的問題,相對于常規的幾何問題,函數背景為問題賦予了“數”的特性.通常可將問題分為三種情形:一是關于坐標軸或平行于坐標軸的直線對稱;二是關于特殊直線對稱,如y=x;三是關于一般直線對稱.前兩種情形,對稱關系有著鮮明的坐標規律,在數值和符號兩方面均有體現.而對于情形三,則可以采用下面三大策略來解.
3.2.1 中點坐標公式

圖5
連接兩對稱點,則兩點所在直線與對稱軸所在的直線為垂直關系,且兩直線的交點為兩對稱點連線段的中點,三點坐標滿足中點坐標公式.以圖5為例,點C和D關于直線l2對稱,且位于直線l1上,則直線l1和l2的斜率之積為-1,B為線段CD的中點,則xD+xC=2xB,yD+yC=2yB.
3.2.2 點到直線的距離公式
根據對稱性可知,兩對稱點到對稱軸的距離相等.故對于已知曲線或直線上點的對稱問題,可設出該點的坐標,然后利用點到直線的距離公式構建方程求解.以圖5為例,若點D滿足方程y=kx+b,且已知點C的坐標及直線l2的方程,則可設點D(x,kx+b),先求出點C到直線l2的距離,再利用距離公式構建點D到直線l2的距離方程,進而求解.
3.2.3 構建全等模型
兩點關于某一固定直線對稱,則可依托直線上固定兩點構建全等三角形,后續通過求線段長求解.另外,也可通過幾何推導求線段長確定所求點的坐標.
上述考題第(3)問在求解時就采用了該方法,下面結合一道例題進一步強化鞏固.

圖6
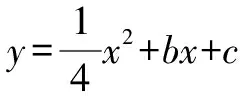
(1)求該拋物線的解析式;
(2)求點A關于直線y=2x的對稱點A′的坐標,并判斷點A′是否位于該拋物線上.


圖7
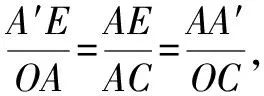
4 寫在最后
上述對一道函數與幾何綜合題開展分步突破,并探究問題的解法,其中三角形相似與點的對稱屬于典型問題,問題的“數”“形”屬性十分突出.數形結合分析,幾何視角切入,運算推理定位,是破題的有效策略.教學中,建議引導學生把握圖象的特征,提取特殊圖形,結合特性推理,充分拓展學生的解題思維.

