GeoGebra環境下一類圓錐曲線動點性質探究的思維可視化教學實驗
鹿亞梅
(寧波市北侖區泰河中學 浙江寧波 315800)
由于數學學科的抽象性,在日常教學中,想要提高學生的學習興趣與學習積極性,就需要新的教學理念以及新的教學工具來輔助教學。GeoGebra作為一款“專為教與學的動態教學軟件”,能實現幾何作圖、代數運算和數據處理等的跨平臺聯動,是實現思維可視化教學的有力工具[1]。所謂思維可視化,指以圖示或圖示組合的方式,把原本不可見的思維結構、思考路徑及方法呈現出來,使其清晰可見的過程[2]。
新課程改革不僅在教學理念上進行了變革,更在教學模式上進行了拓展與創新。部分高中數學教師對信息技術輔助教學的認識不夠深入,主要分為以下兩種錯誤觀念。一是錯誤地認為使用信息技術對輔助日常教學無任何意義,依然堅持使用傳統教學方式,拒絕使用任何信息技術手段。只有當應付上級教研部門聽課或調研時,才做出適當改變。另一種是認為信息技術作為一種現代化的教學手段,代表著教學的進步,故應該摒棄傳統的教學手段,充分利用信息技術。新課標指出,教師要適應時代的發展,按照課程標準的要求,發揮信息技術直觀便捷、資源豐富的優勢,幫助學生發展數學學科核心素養。
本人對一些一線教師進行了調查,發現許多教師未聽說過GeoGebra這個軟件,更不必說用GeoGebra輔助教學了。教師缺乏專業的信息素養,將導致在日常教學中,無法有效地利用信息技術輔助教學。教師是課堂教學的主導者,創新教學的前提是教師具備完善的專業素養,才能實現學生的全面發展。適當使用信息技術,能提高課堂教學效率,加強和學生之間的交流互動,引導學生主動探究,調動課堂學習氣氛,發揮學生的主體作用,培養學生的數學核心素養。因此,在新課改背景下,將GeoGebra教學軟件應用到高中數學課程中至關重要。
一、課題選題背景
浙江的高考中,圓錐曲線是每年的必考內容。筆者所任教的非重點學校的兩個高三文科班在解決解析幾何大題時,經常因為沒有解題思路或者運算能力較弱失分過重。尤其在今年五月份我校自主命題的高二下月考考試中,兩個班級圓錐曲線大題均獲得了平均分不到5分的成績。基于此原因,筆者痛定思痛,思考如何能有效提升學生在圓錐曲線相關內容題目的解題能力、解題自信以及重拾對數學學科的學習興趣。
以月考這道涉及相似橢圓的大題——已知點 p(xo,yo)是坐標平面內一點,且在橢圓C的外部,其中橢圓C:上存在不同的兩點A,B滿足P A,P B 的中點E,F均在橢圓C上,O為坐標原點。
(1)若M為AB的中點,求證:P,O,M三點共線;
(2)若xo,yo為定值,求直線AB的方程;
(3)若P是橢圓上的一動點,求證:ΔPAB的面積為定值,并求出該定值”為背景,筆者通過GeoGebra教學軟件探究出了一類圓錐曲線動點性質,并思考能否通過GeoGebra輔助圓錐曲線教學。基于以上設想,設計了GeoGebra環境下一類圓錐曲線動點性質探究的思維可視化教學實驗。
二、實驗過程
1.前期準備——圓錐曲線章節學習情況的診斷分析
(1)調查對象
該問卷調查對象為筆者所任教的兩個班級,現共有78人(原共有95人,調查時美術生在外培訓,故不予統計)。
在進行教學實驗前,對兩個班級發放問卷,學生填完問卷后立即收回。本次調查共發放問卷78份,回收有效問卷72份。
(3)信、效度分析
信度分析:使用 SPSS軟件對問卷結果進行信度分析,表1中,由于克隆巴赫 Alpha系數=0.886>0.7,說明整體量表的可靠性較好。

表1 可靠性統計
效度分析:由表2可知,KMO取樣適切性量數為0.910,說明該數據適合進行因子分析。Bartlett球形檢驗中,p=0.000<0.05,符合球形檢驗標準。

表2 KMO檢驗和Bartlett球形檢驗
(4)結果分析
問卷共設有11題,其中1-2題調查學生對圓錐曲線的情感和態度,3-4題調查學生對圓錐曲線知識的理解程度以及作圖的態度,5-11題則是調查學生對于教師利用GeoGebra教學軟件輔助教學的態度。
由圖1可知,大多數學生對于教師利用GeoGebra輔助教學持積極態度,表示歡迎。
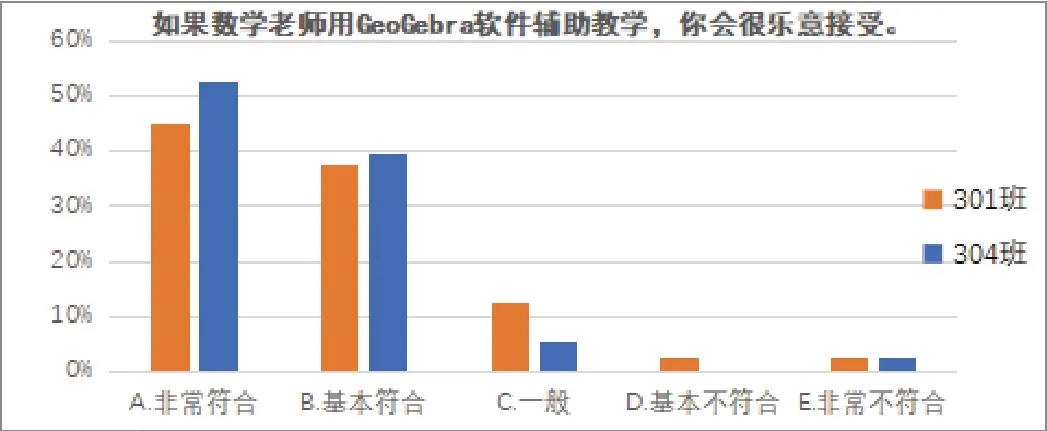
圖1 學生對教師利用GeoGebra輔助教學的態度
2.GeoGebra環境下一類圓錐曲線動點性質探究的思維可視化教學實驗
(1)前測
在進行教學實驗前,將兩個班級參加的慈溪市高二下學期期末試卷中的圓錐曲線相關內容成績作為兩個班級學生的前測水平,此次考試僅有21題(滿分15份)與圓錐曲線有關。使用SPSS軟件對成績進行分析,結果如表所示:
由表3和表4可知,兩班均值差值為 0.36分。檢驗結果表明,顯著性=0.305>0.05,說明方差為齊性,從雙側P=0.355>0.05,能夠得出以下結論,即兩個班的成績無顯著性差異。

表3 對照組與實驗組的前測成績統計表

表4 對照組與實驗組的前測獨立樣本 T 檢驗
(2)教學實驗
實驗時長3個月,對照班教學地點在常規教室,采用傳統教學模式,以PPT演示和講授為主。實驗班在機房上課,采用思維可視化教學模式(圖2)。
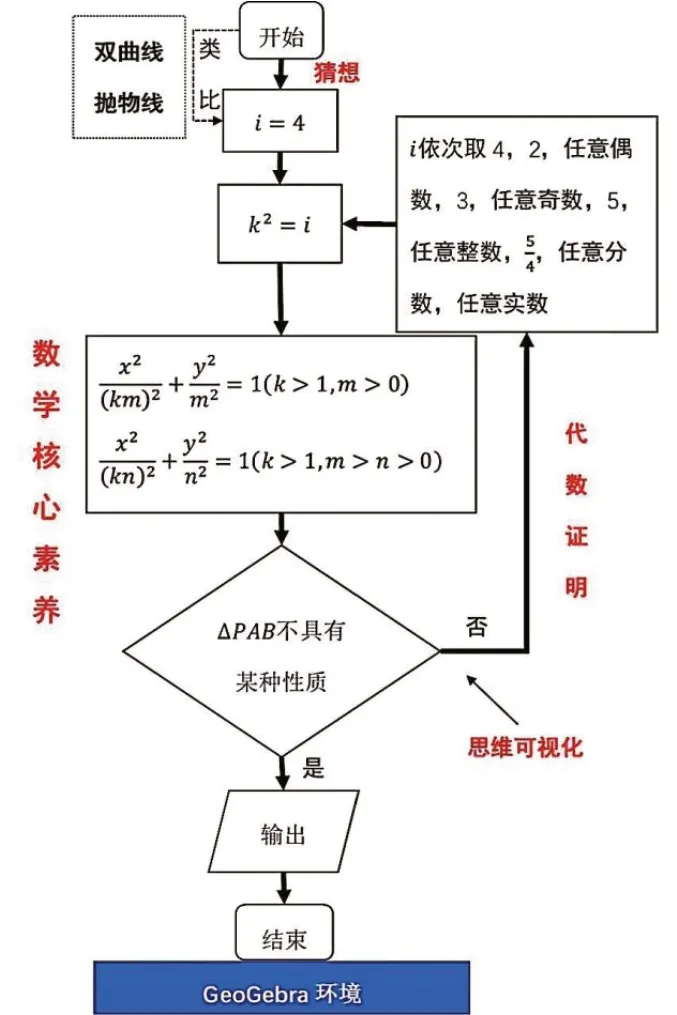
圖2 相似橢圓動點性質探究思維流程圖
首先在GeoGebra代數區輸入指令,兩個橢圓方程滿足形式,此時k2=4啟動動畫,可觀察到 ΔPAB面積始終是定值4.36.模擬多組數值,發現k2=4時,結論皆成立。下面舉例說明k2依次取任意偶數,任意奇數,任意整數,任意分數,任意實數時,結論也成立。令k2依次取4,2,3,5/4,啟動動畫,可觀察到ΔP AB 面積始終是定值。學生可以利用GeoGebra教學軟件動手實踐,體會從特殊到一般、從抽象到具體以及數形結合的思想方法,并在探究的過程中,有效落實數學核心素養,培養學生自主探究能力。
(3)后測
在實驗后期,為檢驗GeoGebra環境下思維可視化教學是否能有效改善圓錐曲線實際教學效果,將兩個班級參加的2021學年第一學期浙江省“七彩陽光”新高考研究聯盟返校考試卷中的圓錐曲線相關內容成績作為兩個班級學生的后測水平,此次考試第9題以及21題(滿分19份)與復習內容圓錐曲線有關。結果分析如下:
由表5和表6可知,兩班均值差值升高為為 0.87分。檢驗結果表明,顯著性=0.640>0.05,說明方差為齊性,從雙側P=0.075接近0.05,能夠得出以下結論,即兩個班的成績有差異。所以,可以認為GeoGebra環境下思維可視化教學能改善圓錐曲線實際教學效果。

表5 對照組與實驗組的后測成績統計表

表6 對照組與實驗組的后測獨立樣本 T 檢驗
三、探后反思
1.重視信息技術的應用,實施可視化教學
《普通高中數學課程標準(2017 年版)》指出,教師應重視信息技術的應用,實現信息技術與數學課程的深度融合[3]。在本文的研究中,由于一類圓錐曲線模型的抽象性,筆者借助GeoGebra來輔助教學,以提高學生的學習興趣與學習積極性。
2.開展數學探究活動,促核心素養落地
在新教材改革的背景下,教師適當開展數學探究活動,有利于核心素養的落實。本文借助GeoGebra教學軟件進行實驗探究將一類圓錐曲線動點性質進行推廣,在經歷“觀察—猜想—歸納—驗證”的探究過程中,促數學核心素養落地。

