動態規劃及其算法應用

文超婷 沈秋銘 姚仁杰 李雙喜

牡丹江師范學院計算機與信息技術學院 黑龍江牡丹江 157011

1 概述

動態規劃類似于分治法。將一些待解決的問題全部分割為一個一個的小問題分別解決，一般情況下，動態規劃函數是指利用子問題的重疊關系可以得到求解問題的遞歸關系。得到遞歸關系之后，就可以利用這個關系來求解問題，這也就是動態規劃函數。采用動態規劃算法將子問題的解通過分析表格數據存儲下來，相較于分治法處理獨立子問題而言，記憶化搜索可以有效地解決分治法中重復求解子問題的效率問題。

2 動態規劃求解過程

動態規劃的本質是對問題進行定義之后建立狀態轉移的方程。我們可以將動態規劃的理論理解為將想要探究的問題劃分成若干個小的子問題，這些子問題都有相應的解。在這些可行的解決方案中，必須有一個最優的解決方案。

如何合理地推導出求解最優值的方程，正確地找到臨界值，是進行動態規劃方法過程中的基本的要求。基于此，研究某個問題時先要把研究對象劃分為N個密不可分的子對象，推算出其中的各個重要變量和最優值方程式，這樣就把研究對象劃分為N個子對象，一一推導尋求出結果。每一個臨界條件，都有一個臨界值，再一次求解，這樣在每一個子過程求解中都可以找到最優化的結果，這樣重復操作，就可以得到最后一個方程的結果，并且也可以得到研究對象的最佳計算結果。

對多個子對象的研究過程中，通常動態規劃方法不同于當前對象和未來子對象，然而綜合考慮當前和未來是解決最優化的關鍵所在，每個子對象的研究結果都要綜合全局考慮，又不同于每個子對象的最優研究結果。

在求解研究對象的最佳解決方案的時候，初始條件已知，每個子對象的結果都是該子對象的狀態函數，因此最優解也是通過各個子對象的各個狀態一一變換時所得到的。

動態規劃算法是否有效主要取決于下述的兩個方面，首先，是子問題的最佳結構，其次，是子問題是否具有重疊性。

(1)最優子結構：當該問題的最佳解決方案包括了下層子問題的最優解的時候，可以說該子結構具有良好的性質。

(2)重疊子問題：當使用自頂向下的遞歸方法解決問題時，使用的每一個子問題都不一定是新產生的，有的時候，我們需要反復多次的計算其中的一部分子問題。在動態規劃方法中，每個子問題只能求解一次，但由于子問題是重疊的，所有子問題都可以存在于表中，未來我們解決問題的同時可以盡可能多地使用這些子問題的解。

實現動態規劃算法一般可以分為自頂向下遞歸或者自底向上遞推的方法。

自頂向下是指，先劃分整個數組，然后再劃分子數組，直到我們所有子數組只包含一個重要元素，然后逐層合并。因此，最好使用遞歸來實現這一點。

自底而上是指，對整個陣列世界進行合并，可以合并相鄰的兩個元素，然后再對相鄰的四個元素進行合并，直到將所有的數組都合并了之后，可以完成排序。

在使用動態規劃來處理這個問題時，我們首先需要得到最佳解決方案的基本性質，找到其基本的結構，然后可以使用上文中的遞歸的方法來找到最佳的計算結果。將問題進行細化分解后，再把每一個子問題得到的最優值的有效信息通過表格形式存放，最后利用問題之間的重疊聯系得到解決問題的方程組，以獲得最優解的具體結果。

3 應用分析

3.1 最長公共子序列(Longest Common Subsequence)

問題描述。給兩個字符串S1以及S2，求子序列在S1中且子序列也在S2中的字符串，所得的字符串的最大長度為多少。

首先定義子問題，設F(i，j)表示序列S1={x1，x2，…xn}和序列S2={y1，y2…ym}表示為最長公共子序列的長度，那么初始的子問題為序列S1和S2至少有一個空序列，因此S1和S2與空序列之間的最長公共子序列均為0，即F(i，0)=F(j，0)=F(0，0)=0。

根據圖1關于字符串asdfgh以及字符串adsdg的狀態矩陣，使用F[i][j]表示字符串前i個字符以及前j個字符的最長公共子序列長度。

該題目對于集合的劃分有四種情況。

(1)S1[i]不在集合中，S2[j]也不在集合中。

(2)S1[i]不在集合中，S2[j]在集合中。maxlength=F[i-1][j]，由于F[i-1][j]表示在S1和S2中前i-1個字符以及前j個字符出現，但是S2[j]不一定會在F[i-1][j]的集合中出現，與條件中的S1[i]不在集合中，S2[j]在集合中不符，但是在動態規劃函數中，依然可以用F[i-1][j]來表示，因為這個條件是F[i-1][j]的一個子集，而我們所需要獲取的是maxlength，所以使用F[i-1][j]對maxlength的結果并不會造成影響。

(3)S1[i]在集合中，b[j]不在集合中。原理同(2)，采用F[i][j-1]表示。

(4)S2[i]在集合中，b[j]也在集合中。則maxlength=F[i-1][j-1]+1。

在實際計算中，情況(1)被包含在情況(2)(3)，因此只需要將問題劃分為兩種可能。

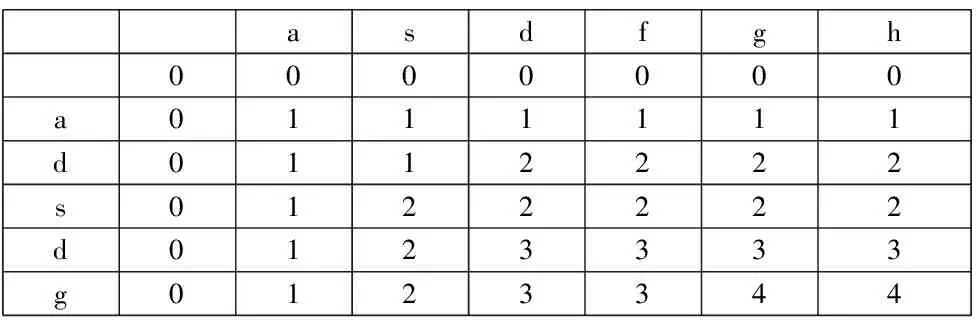
字符串asdfgh與字符串adsdg的狀態矩陣表

則有如下動態規劃函數：

對于該問題給出以下算法：

void LCS()

{

cin>>n>>m；

cin>>a+1>>b+1；

for(int i=1；i<=n；i++)

for(int j=1；j<=m；j++)

{

F[i][j]=max(F[i-1][j]，F[i][j-1])；//②和③的情況一定存在，所以可以無條件優先判斷

if(a[i]==b[j])F[i][j]=max(F[i][j]，F[i-1][j-1]+1)；

}

cout<

}

3.2 0-1背包問題

問題描述。假設有一個背包，里面有很多東西，并且東西都有一定的價值。如果數量為n，且每件物品只能裝入背包一次，在不超過背包容量的情況下，這個背包可以裝入的總價值是多少？

我們將前i個物品，背包容量為j的最優解的狀態設為F(i，j)，Capacity[i]為第i個物品所需的背包容量，第i個物品的價值由Value[i]來表示，目前的狀態的最優解與前一個的狀態的最優解有關，處于依賴關系，將F(0，0)設為初始狀態，也就是第0個物品裝入背包容量j=0的狀態下F(0，0)=0，當我們將第0個物品裝入背包容量j大于或者等于0或者前i個物品裝入背包容量j為0時的情況下狀態F(i，j)=0，由此可得F(0，j)=F(i，0)=0。由此可得背包容量比物品的重量小，j<第i個物品所需容量，即Capacity[i]，則第i個物品不能裝入背包內，因此前i個物品能裝入背包的價值最優解也就是前i-1個物品能裝入背包的價值最優解，由此可得F[i][j]=F[i-1][j]。

當背包容量足以放入第i個物品，也就是j>Capacity[i]，那么我們需要做出選擇，是否把第i個物品也放在里面。如果選擇裝入可得方程為：F[i][j]=F[i-1][j-Capacity[i]]+Value[i]；不裝入的話可以得到，F[i][j]=F[i-1][j]，最后為了得到選與不選的最優解，需要對兩種情況進行比較，得到的最大值max則為當前狀態下的最優解。則有如下動態規劃函數：

對于該問題給出以下算法：

void bag()

{

int n，m；

cin>>n>>m；

for(int i=1；i <=n；i++)

cin>>Capacity[i]>>Value[i]；

for(int i=1；i<=n；i++)

for(int j=1；j<=m；j++)

{

if(j

F[i][j]=F[i-1][j]；

else

F[i][j]=max(F[i-1][j]，F[i-1][j-Capacity[i]]+Value[i])；

}

cout<

}

根據以上分析，可以優化為一維動態規劃求解。

首先，我們需要明確為什么可以簡化二維的動態規劃求解的思想為一維解法，因為第i項的最優值依賴并且只依賴于第i-1項的最優值，也就是說無論是i-2，i-3等的最優狀態都不需要被第i項的求解使用。在背包問題上，每一個物品結束選擇之后，該物品的體積和價值對于之后的最優值計算不會被利用，因此我們將二維壓縮為一維即可以有效節省空間復雜度。

其次，我們需要了解當二維被簡化，用一維解題時，為什么需要用逆序的方式來更新當前背包的容量的最優結果，也就是j從Capacity開始向下更新。在我們對F一維數組進行更新時，只有上一層的F數組中的數值，因此在更新下標較大的數組數值時，其上一層的F數組數值保持原始值，沒被更新。所以在進行背包問題的最優問題簡化到一維求解，我們需要將其的索引值從背包的總容量逐步減小進行更新。

定義狀態F[j]在背包容量為j的情況下，裝有N件物品的最優解，由于采用一維解法，所以利用逆向思維將背包容量j從背包的最大容量開始枚舉。由此得到狀態轉移方程為F[j]=max(F[j]，F[j-Capacity[i]]+Value[i])。

對于該問題給出以下算法：

void bag_plus()

{

int n，m；

cin>>n>>m；

for(int i=1；i<=n；i++)

{

int Capacity，Value；

cin>>Capacity>>Value；

for(int j=m；j>=Capacity；j--)

F[j]=max(F[j]，F[j-Capacity]+Value)；

}

cout<

}

結語

采用動態規劃算法以最長子序列和背包問題為切入點進行研究，探究求得最優解的方法，在最長子序列和背包問題中通過比較兩種情況(b[j]不在集合中/是否裝入第i個物品)分別分析兩種情況的結果，得出動態規劃函數，然后給出對應算法。動態規劃算法無論是在日常生活還是在程序設計實訓和競賽中，都有著顯著的算法地位并且被廣泛使用。本研究的結果意味著當解決相關的最優解問題時，采用動態規劃算法可以有效地對時間復雜度和空間復雜度進行優化和減少。后續研究中，將繼續尋找優化最優解問題的其他思想。