參數變點線性回歸模型的LR檢驗

石美麗

延安大學數學與計算機科學學院 陜西延安 716000

1 概述

變點問題淵源已久，可以追溯到1954年Page關于連續抽樣檢驗的討論。自20世紀70年代以來，對于變點問題的探討以及對變點性質的研究一直是統計界的熱門話題。比如，在工業自動控制中的質量檢測、在經濟與金融中的數據分析、氣象中的天氣預測、流行病學中傳染率的研究以及導航系統分析和心電圖中的韻律分析等方面有大量的應用背景。而進入21世紀以來，隨著科技的發展，我們所關心的問題面臨著大規模數據的挑戰，這種數據往往以張量的形式呈現。因此，變點問題的研究又迎來了一個高峰時期，而對于變點的研究，我們首先關心的是存在與否的問題。所以，應用數理統計方法對于變點進行檢驗是十分必要的。

Quandt(1958)最早提出來兩階段回歸模型，即至多含有一個變點(AMOC)模型，利用最大似然法對簡單回歸模型中的參數進行估計，并在1960年利用似然比檢驗對于變點的存在性進行檢測。而Quandt有關變點的估計與假設檢驗問題是基于小樣本的。Kim(1989)利用似然比檢驗研究了AMOC的一元線性模型中的截距項的變點問題，并于1994年使用似然比檢驗統計量研究了一般線性回歸模型中變點的檢測問題。陳希孺1991年的變點統計分析簡介中，討論了包含多個變點的研究是在含有一個基礎上的“量變”。并且Bai(1998)將純參數變點問題推廣到局部參數變點，對線性模型中的變點問題研究做了很好的補充。因此，對于AMOC模型的變點問題研究具有更廣泛的意義。

Kolda(2006)，Kolda和Bader(2009)，Lu(2019)，Zhang(2019)等對張量分解進行大量研究，并且在此基礎上運用于我們生活當中，如衛星健康監測問題[馬友等(2020)]，信息工程自動化控制[Zhang等(2016)，Li等(2018)，Zhang等(2019)，Zhang等(2020)，Wang等(2020)]，醫學診斷問題[Crainiceanu等(2011)；Allen等(2011)；Hoff(2011)；Aston和Kirch(2012)；Zhou等(2013)，Kilmei13等(2013)，Li等(2018)]。后者Zhou等與Li等分別基于張量的CP分解和Tucker分解構造出神經成像與臨床結果之間的廣義線性模型，并研究了點估計量及其大樣本性質。并且基于張量的CP分解以及Tucker分解，我們(2020)以及徐常青等(2021)進一步探討了參數張量的估計，給張量變點問題提供了大量的研究基礎。

本論文從變點理論的研究背景出發，基于正態分布假設，對最多含有一個參數變點的線性回歸模型的參數變點進行統計推斷和預測估計。若變點位置已知，關于變點位置是否存在的檢驗問題，在正態假設的基礎下，我們可以用F檢驗，因此以下的討論過程中，我們只考慮變點位置不知道的情形。并且由于正態假設，可以證明LR方法、方法以及LM方法在檢驗和估計問題上是等價的，所以本文中我們僅僅討論LR方法分別在一般線性回歸模型以及張量線性回歸模型中的運用。

2 參數變點檢驗

2.1 向量情形

對于一元線性回歸模型，即=+(=1，…，)，Kim和Siegmund(1989)考慮了至多一個變化點的似然比檢驗，并推導出檢驗顯著性水平的解析近似。并且Kim(1994)進一步將其推廣在多元的情況，研究其檢驗和統計推斷問題。這里我們討論多元情況，模型如下：

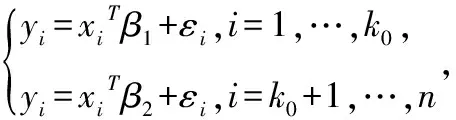
(2.1)

其中表示可能的變點位置，=(1，，1，…，，-1)一般假設是i.i.d.的，且服從均值為(|)=0，方差為(|)=的正態分布。

變點是否存在等價于如下假設檢驗問題：

：=?：≠.

當=時，令:

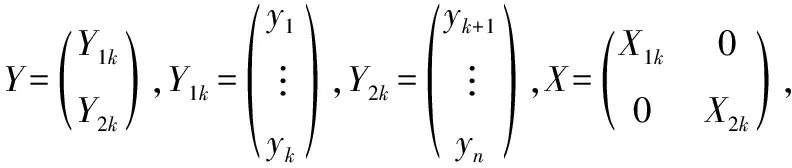
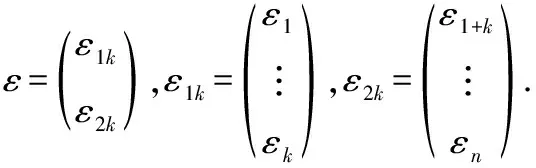
則模型(2.1)矩陣形式等價于：

=+.

令=(1，-1)，上述假設檢驗等價于:

：=0?：≠0

由LR檢驗構造似然比檢驗統計量

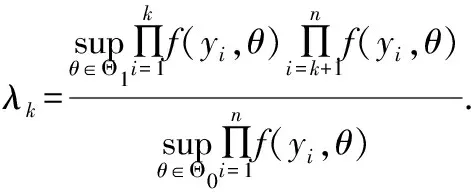
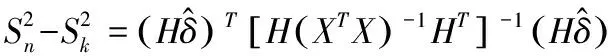
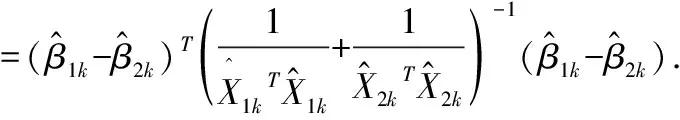
由于是未知的，所以檢驗統計量為:

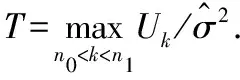
其中是一個維的布朗橋，1<<<，Kim和Cai有關于，的具體討論。

2.2 張量情形

考慮到張量分解結構的復雜性，以及類比矩陣的譜分解，我們對D階張量∈×…×做如下設定，

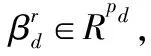
對于一般的張量線性回歸模型:

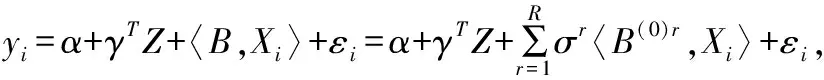
其中是截距項，∈是向量系數，是張量系數。關于以及在AMOC模型中的討論，具體辦法(2.1)及概述中已涉及，這里不再贅述。我們這里只討論最簡單的情況，即=1時，模型如下，

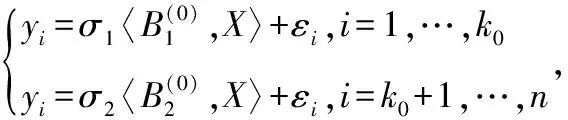
(2.2)

由于本質仍然是D階張量，作為變化參數相對復雜，所以這里我們將看成冗余參數，只考慮半參變化，即關于模型(2.2)有如下假設檢驗，

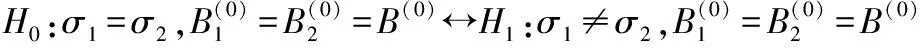
模型(2.2)的矩陣形式為:

=+，

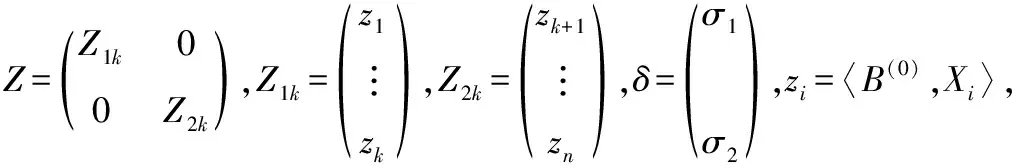
：=0?：≠0

由正態假設下，LR檢驗的特殊性，有:

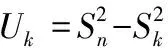
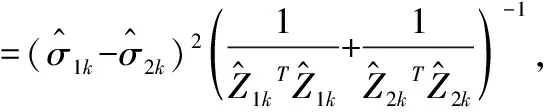
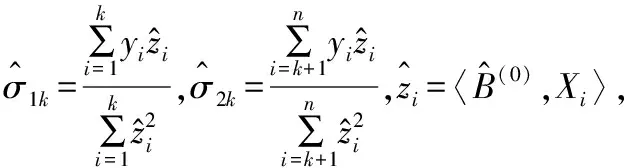
由于是未知的，所以檢驗統計量為:

當>時，我們就可以拒絕原假設，接受備擇假設。

這里需要明白，關于判定是否接受原假設，更好的辦法是，知道統計量的極限分布，然后給定置信區間。這也是我們接下來要研究的部分，以及將其推廣到廣義線性，更進一步可以結合張量Tucker分解進行討論。

結語

本文總結了AMOC線性回歸模型中參數的統計性質，以及將變量從向量擴展到張量的形式，給出LR檢驗對應的檢驗統計量，給我們進一步的工作打下基礎。接下來我們可以考慮其大樣本性質，以及張量中其他參數或多個參數作為結構變化的影響者的情形。進一步可以結合張量的Tucker分解將其擴展到廣義線性模型。