基于對數正態分布的新型冠狀病毒肺炎病例統計特征分析

趙宜賓, 張艷芳, 任晴晴

(防災科技學院基礎部，河北 三河 065201)

0 引言

自2019 年12 月以來，湖北省武漢市發現多起不明原因的病毒性肺炎病例，經醫學專家證實為一種新型冠狀病毒感染所致。2020 年1 月20 日世界衛生組織將其命名2019 新型冠狀病毒即COVID-19。自從COVID-19 出現后，迅速在湖北擴散，發病人數不斷上升。天津第一位病例是從武漢旅游回來發病，隨后確診。由于交通網絡發達，而且正值春節前夕，人口流動大，病例通過各渠道迅速傳播，發病人數不斷上升。2020 年1 月21 日，自天津發布了首例輸入性COVID-19 確診病例，天津積極采取防控措施，明確了涉外疫情防控和入境人員健康管理規定。為了幫助大家了解疫情發展狀況減少群眾恐慌，國內外學者都積極投入到有關疫情的研究中，很多醫學工作者從患病者癥狀和治療過程情況進行研究[1–3]。早前的學者應用微分方程模型研究流行病的發展趨勢[4]，針對新冠疫情的傳染特點，從事數學工作的學者也應用微分方程動力系統和數據分析方法對疫情發展趨勢進行分析和預測[5–8]。嚴閱等[9]建立了一類基于時滯動力學系統的傳染病動力學模型，通過該模型反演出了各地的傳染率和隔離率，并預測了各地的疫情發展趨勢。王志心等[10]通過機器學習對確診人數趨勢進行了預測。耿輝等[11]給出多種相關干預措施下疫情發展趨勢的預測。通過統計分析方法進行系統建模，挖掘研究對象的發展規律[12]被證明是高效的。劉海濤等[13]利用正態分布較好地模擬巖樣的聲波測試結果。Sarkar 等[14]通過威布爾分布給出了合理應用風能的相關參數。在傳染病的研究中，潛伏期的規律分析[15–17]對于疫情防控和后期治療有重要的意義，這也是本文研究主要內容。

本文以天津市2020 年1 月21 日至2 月27 日確診的136 位病例數據為源數據，以接觸時間和發病時間明確為主要依據，篩選出84 例樣本做為研究數據，以對數正態分布模型和單因素方差分析為主要研究工具，對于新型冠狀病毒的潛伏期特征進行全面分析。

1 天津疫情概況分析

1.1 數據來源與特點

數據來源為天津市政務網(www.tj.gov.cn)上通報的從2020 年1 月21 日至2 月27 日在天津地區確診的136 例新型冠狀病毒病例樣本，此樣本也是截止到2020 年3 月7 日天津疫情基本結束的天津地區全部病例樣本。

本文研究樣本具有以下3 個特點。

1) 數據信息比較完整

天津確診病例信息對于接觸、發病、確診時間記錄相對完整，對于病例的流動和接觸途徑，以及病例間的關聯關系記敘明晰，數據鏈相對完整。

2) 病源輸入相對固定

天津疫情的輸入病源主要是動車職工、百貨大樓銷售員、和個別輸入病例，數據單一可使接觸時間確定相對準確。

3) 數據噪聲小

天津市疫情防控措施及時到位，對于病例發現、隔離、救治過程科學合理，同時天津市的人口流動性相對較小，病例之間的交叉感染機率極大降低，數據信息比較真實。

以上樣本特點決定了數據信息的真實、可靠，據此用科學方法分析出的結論，對于病源的數理特征的反映是真實可靠的。

1.2 數據清洗方案

截止2020 年3 月7 日，天津市共有確診的新冠病毒肺炎病例136 例，舍棄與確診患者或病源沒有明確接觸時間的樣本，并依據如下原則確定病毒感染時間。

原則1如果有明確接觸時間的，感染時間確定為接觸時間。比如，2020 年1 月20 日到百貨大樓購物，則感染時間定在2020 年1 月20 日。

原則2如果可觸時間是時間段，3 天以內的以第2 天作為感染時間，超過3 天的，以第3 天作為感染時間。比如，2020 年1 月21 日至1 月25 日曾到武漢出差，則病毒感染時間定為2020 年1 月23 日。

原則3如果是同住親屬，病毒感染時間相同。如果親屬接觸感染，則以接觸日作為感染時間。

在此基礎上，定義病毒潛伏期為從健康個體感染病毒到新冠肺炎病癥特征出現的間隔期。依上述原則，篩選84 個病毒感染時間明確的病例作為病毒潛伏期的研究樣本。

對于樣本中的3 例無癥狀感染者，潛伏期定義為患者病毒感染至確診的時間間隔。

1.3 樣本數據特征概述

對選定的研究樣本做簡單的數字特征統計分析，如表1 所示。集中趨勢的三個度量指標基本一致，約為11 天，潛伏期的偏度和峰度兩個數字特征均大于1，表明分布呈尖峰態且右偏，由于個別病例潛伏期超長，故概率密度曲線存在右側拖尾現象。

表1 病毒潛伏期數字特征統計分析

對樣本的簡單統計分析顯示樣本具有對數正態分布的相關特征。

進一步，對樣本做是否服從對數正態分布的非參K-S(Kolmogorov-Smirnov)檢驗，得統計量D=0.118 95，檢驗的p值為0.171 2?0.05，即潛伏期的統計分布與對數正態分布無顯著差異。因此，假定潛伏天數服從對數正態分布是合理的，故下文將用對數正態分布來描述潛伏期的統計規律。

2 基于對數正態分布的潛伏期特征描述

為了能夠對病毒潛伏期規律從機理上有更客觀清晰的描述，首先，介紹關于超出量和對數正態分布的相關理論知識。

2.1 統計分布超出量相關概念

為了能夠對隨機變量的統計規律做更完備的描述，文獻[18]給出了關于分布超出量的相關概念。

定義1[18]若隨機變量X ～F(x)，記

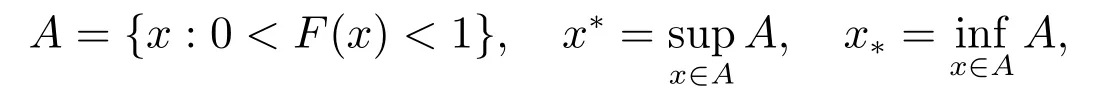
則稱集合A為分布F的支撐，x?和x?分別為分布F支撐的上端點和下端點。

定義2[18]設X1,X2,···,Xn是來自總體X的樣本，總體X的分布函數為F(x)支撐的上端點為x?，對某個任取較大的ux?，稱

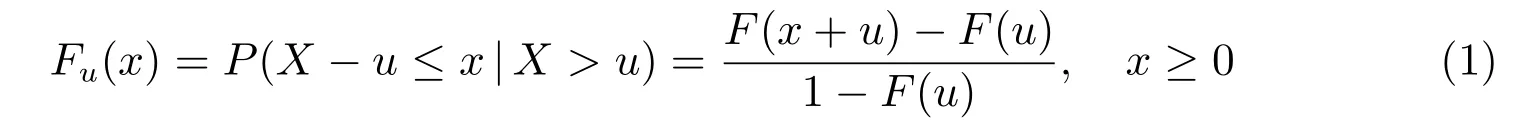
為隨機變量X的超閾值的分布函數，簡稱超出量分布。

由公式(1)超出量分布的概率密度函數為

定義3[18]稱e(u)=E(X ?u|X>u)為隨機變量X的平均超出量函數。

平均超出量函數主要描述隨機變量取值大于給定閾值的部分的平均值，是用于描述隨機變量尾部的重要數字特征，用于對隨機變量的統計規律性的全面完整表述。

2.2 對數正態分布理論概述

定義4設X是取值為正的連續型隨機變量，若lnX服從正態分布，則稱X服從對數正態分布。

若X服從對數正態分布，令其分布函數為F(x)，密度函數為f(x)，則有

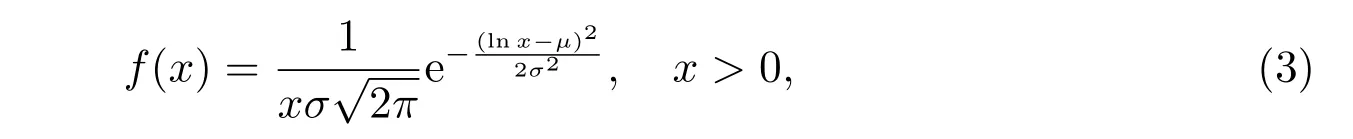
其中μ和σ分別為lnX的均值和標準差。對數正態分布適用于有更大向上波動可能、更小向下波動，且分布具有不對稱性的變量的統計規律的描述。

若X服從對數正態分布，則根據數學期望和方差定義，容易得出

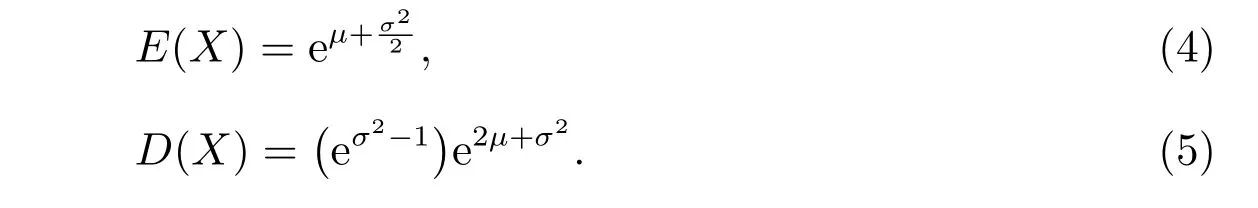
根據定義3，對于給定閾值u可以得出對數正態分布的平均超出量近似為

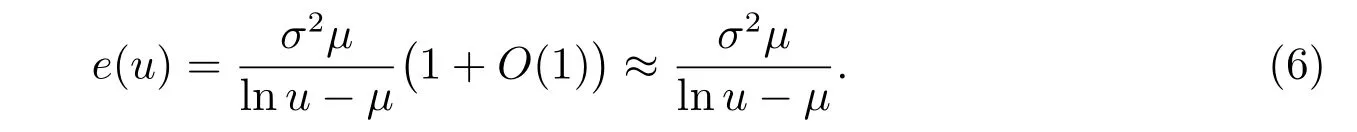
分位數是在用統計分析方法描述研究對象的變化規律時一個十分有效的工具，其定義如下。

定義5若隨機變量X ～F(x)，稱

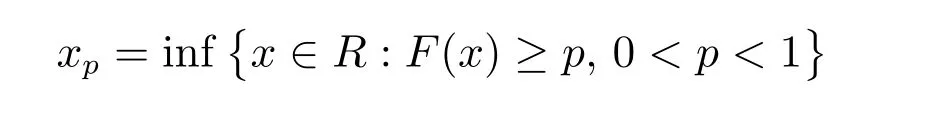
為F的p分位數。

在損失評估中常用分位來表達災害的重現水平或計算重現期。在本文中，若以天為單位的病毒潛伏期X服從對數正態分布，則分位數xp表示p×100%的患者的病毒潛伏期小于xp天。

可用極大似然估計法求得對數正態分布中的參數μ和σ的估計值：令x1,x2,···,xn是一組樣本值，則可得對數似然函數為

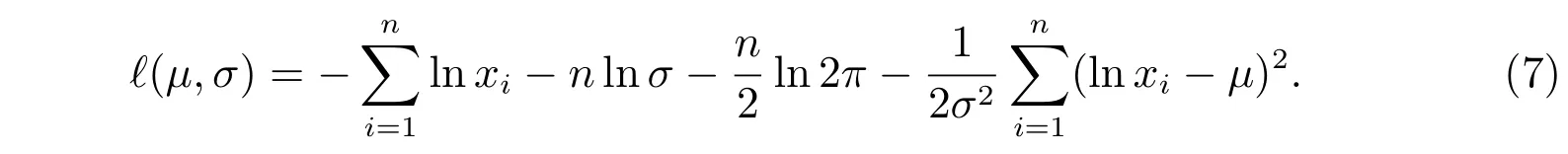
令對數似然函數分別對μ和σ的偏導等于0，可得方程組如下

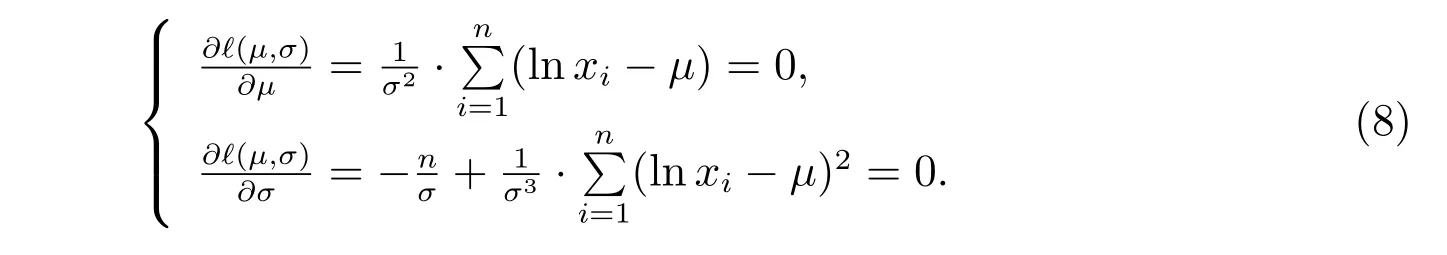
解方程組可得參數的極大似然估計值為

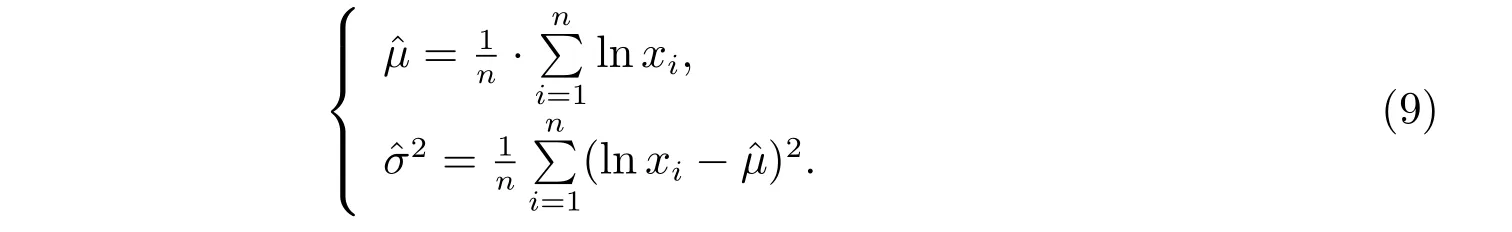
2.3 基于對數正態分布的病毒潛伏期特征分析

利用第1 節選取的研究病毒潛伏期數據樣本，根據公式(9)，可得對數正態分布概率參數的極大似然估計為?μ=2.43, ?σ2=0.21。

模型的適用性檢驗，如圖1。以對數正態分布的分位數為橫軸，以樣本數據分位數為縱軸的對數正態分布QQ 檢驗顯示了數據散點總體上是沿第一象限45?線分布，如圖1(a)所示。經驗分布函數與估計的潛伏期分布曲線契合度較高，如圖1(b)所示。因此，用對數正態分布來描述病毒潛伏期規律是適用的。

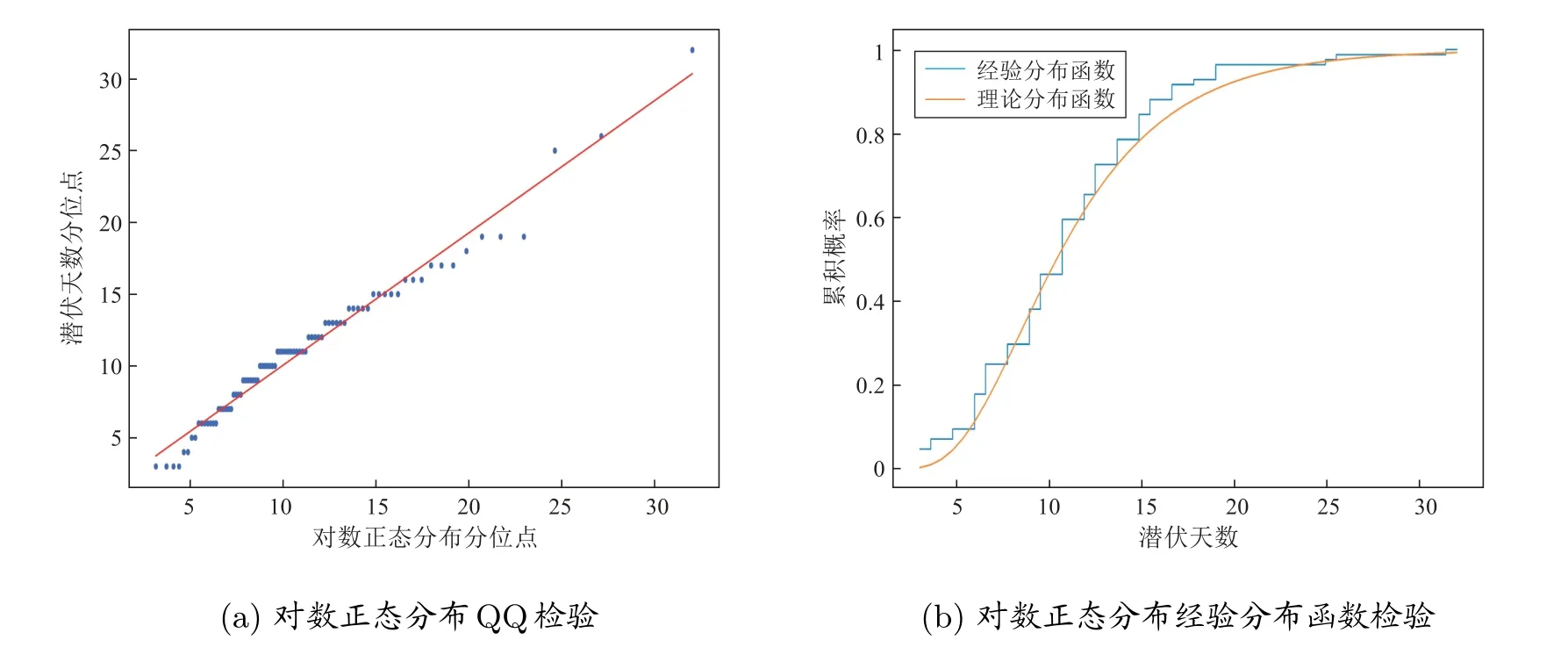
圖1 對數正態分布適用性檢驗

潛伏期的對數正態密度曲線與樣本頻率分布規律，如圖2 所示。

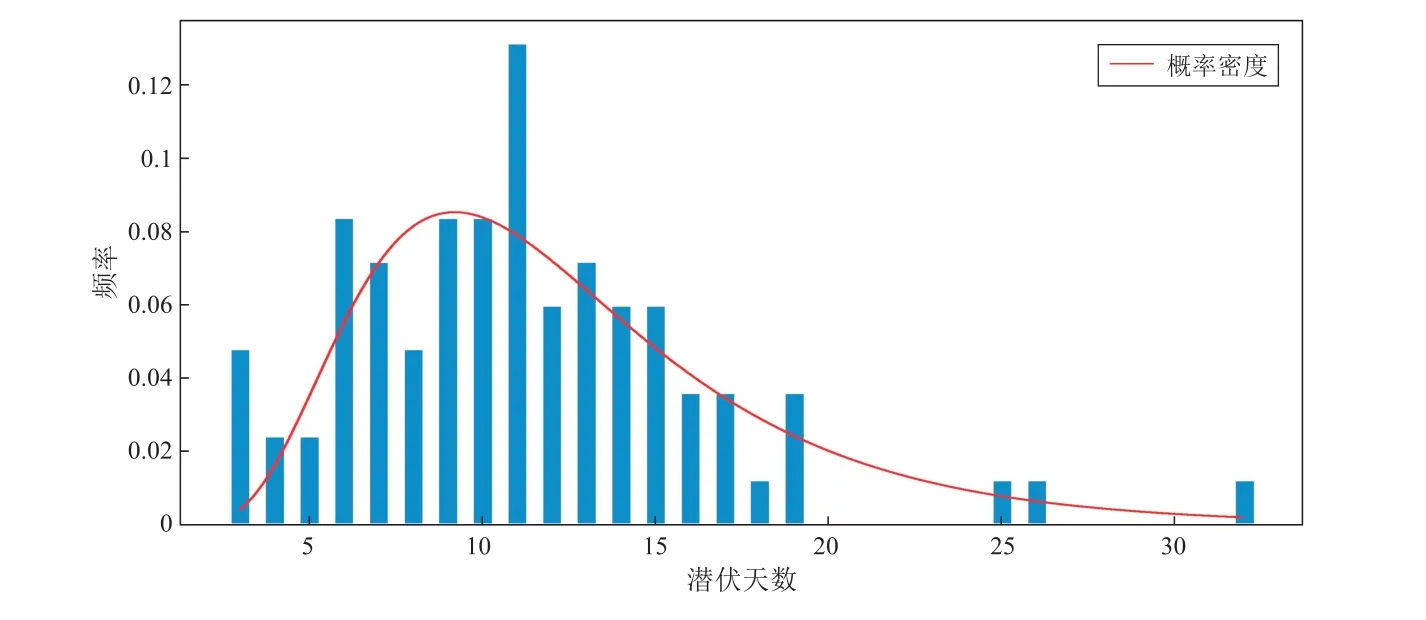
圖2 概率密度 頻率圖

估計的概率密度曲線與潛伏期的頻率直方圖輪廓基本吻合，說明病毒潛伏期統計規律可以用對數正態分布描述。進一步，做樣本值的頻率與相應密度函數值整體的相關性的F檢驗，得統計量F= 18.051 3?1，檢驗p值6.2×10?5?0.05，說明頻率與密度曲線是相關的，計算相關系數R2= 0.7，說明建立的對數正態模型可以解釋樣本數據70%的變異。

綜合上述檢驗結果，利用對數正態分布對潛伏期統計規律進行分析是合理和可信的。

由均值公式(4)，得E(X)≈12.59，表明新冠肺炎病毒的平均潛伏期約13 天，對比現行政策，在防控形勢嚴峻且醫療資源缺乏的情況下，對疑似對象觀察14 天的規定是合理的。但公式(5)計算得方差D(X)≈37.04(標準差約為6.1 天)，說明不同個體的潛伏期長短存在著較大的差別，也就是在疫情防控資源允許的情況下，應該延長對疑似對象的隔離留觀天數，這樣會取得更好的防控效果。

計算分位數可得x0.95≈24，表明95%的患者潛伏期在24 天以內。由式(6)計算x0.95的平均超出量可得e(x0.95)≈6.71，也就是說，約有5%的患者，他們的平均潛伏天數應該是30 天左右，這與已經發現的潛伏期超長的患者數據是相對應的，由于新型冠狀病毒在潛伏期也具有傳染性，所以具有超長潛伏期的這5%的患者將給疫情防控帶來極大困難。因此，在條件允許的情況下，適當延長對密切接觸者的隔離留觀時間是合理，也是必要的。

3 潛伏期影響因素的方差分析

確定新型冠狀肺炎病毒潛伏期的影響因素，對疫情防控有著重要的意義。下面將從年齡、性別和接觸方式上，對病毒潛伏期進行差異性分析。

3.1 數據預處理

簡單數字特征統計分析發現數據有三個異常點，差異性分析前將下面三個異常點去除，如表2 所示，三個異常點均為潛伏期天數超長，這也與當前發現核酸檢測呈現陽性而無癥狀病例相吻合。

表2 異常點數據表

3.2 年齡對病毒潛伏期的影響

按0～18 歲、9～35 歲、36～50 歲、51～65 歲及65 歲以上五個年齡段，對樣本進行分組，對各組分別進行簡單的數字特征分析和正態分布的K-S 檢驗，結果如表3 所示。

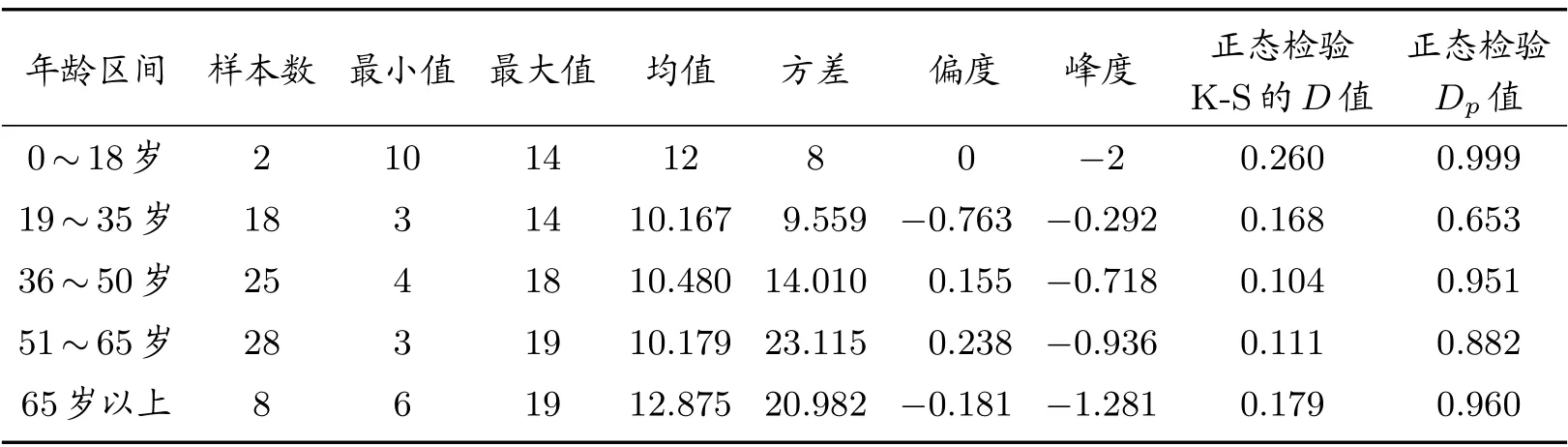
表3 各年齡段病例潛伏期數據統計特征及正態分布檢驗

在0～18 歲年齡段，數據樣本只有兩個，一方面分析結果沒有統計意義。另一方面，是不是真正表明青少年對新冠肺炎具有較強的免疫力，這需要進一步搜集數據進行研究。鑒于此，下面的分析將只對年齡在19 歲以上各組樣本進行。

不同年齡段的數字特征及正態分布K-S 檢驗結果(表3)說明各年齡段病例的潛伏期均可認為服從正態分布(p值?0.05)。同時，各年齡段病例潛伏期方差齊性檢驗p=0.167>0.05，即可認為各樣本方差相等。

在樣本數據服從正態分布，且方差相等的前提下，對各年齡段病例潛伏期均值做單因素方差分析p值= 0.98?0.05。因此，統計意義上講各年齡段潛伏期均值無顯著性差異，即除去疑似異常點后，潛伏期與年齡沒有關系。

3.3 性別對病毒潛伏期的影響

將樣本數據按性別分組，分別進行簡單的數字特征分析和正態分布的K-S 檢驗，結果如表4 所示。

表4 不同性別病例潛伏期數據統計特征及正態分布檢驗

由表4 結果可以看出，男性和女性的潛伏期均可認為服從正態分布(p值?0.05)。同時，兩組病例樣本的潛伏期方差齊性檢驗p=0.11>0.05，即可認為男性和女性樣本的方差相等。

對男性和女性兩組病例潛伏期均值做單因素方差分析p= 0.33?0.05。因此，統計意義上講病毒對于男性和女性的潛伏期均值無顯著性差異，即除去疑似異常點后，潛伏期與性別無關。

3.4 接觸方式對潛伏期的影響

從常規的病理分析來看，一些傳染病的潛伏期會受到傳染途徑的影響，如艾滋病、乙肝的傳染途徑不同，病源量級不同導致潛伏期不同[19]，因此，不同的接觸方式是否對新型冠狀病毒的潛伏期有影響是值得探討的一個問題。

本文將與病源的接觸方式分為生活接觸(與長時間攜帶病源患者較長時間在一起生活)和普通接觸(相對來說，只是短暫相聚或偶遇接觸的情況)，分析在這兩種接觸方式下，潛伏期有無顯著差異。

分別對兩組樣本分別進行數字特征分析和正態分布的K-S 檢驗，結果如表5 所示。

表5 親屬接觸與一般接觸病例潛伏期方差齊性檢驗表

數字特征及K-S 檢驗結果表明，兩組病例的潛伏期均可認為服從正態分布(p值?0.05)。同時，對兩組病例潛伏期方差齊性檢驗p= 0.98?0.05，即兩組數據在統計意義上可認為方差相等。

對兩組病例潛伏期均值做單因素方差分析，由于p= 0.016＜ 0.05，故認為兩組病例的潛伏期均值存在顯著性差異，即對于一般疑似患者來說，與病源接觸時間的長短可能會導致潛伏期的不同，也就是說潛伏期與接觸病源方式有關。

4 模型討論與展望

本文應用統計建模的方法對新型冠狀病毒的潛伏期的數字特征及影響因素做了全面的分析，所得結論與現有的經驗規律相吻合，說明模型是有效的。同時，由超閾值分布得出的超長潛伏期的均值是對現在經驗的有益補充。

本文旨在為傳染病潛伏期特征分析提供一套理論方法，所得的結論是依據所得樣本做出的。所確定因素對潛伏期是否確有影響，需要進一步擴充樣本容量進行深度數據挖掘來驗證。各因素對潛伏期的影響程度及原因，還有待于醫學專家從醫學視角上進一步分析和論證。

由于分析數據只是天津市的病例樣本，分析結果有一定的局限性，各地區病例潛伏期的特征和規律是否相同，在現有確診方案下，病例的確診時間具有何種特征等內容將是作者后續研究的重點方向。