基于Beverton-Holt出生函數的階段結構傳染病模型的穩定性和分支

胡新利, 鄭田田, 楊亞莉

(1. 西安工程大學理學院，西安 710048; 2. 空軍工程大學基礎部，西安 710051)

0 引言

傳染病一直被認為是威脅人類生存與健康，阻礙社會及經濟發展的最主要危害之一。不僅一些古老傳染病病原體不斷發生變異變遷，新的病原體也層出不窮。據世界衛生組織報道，2017 年，肺炎估計造成808 694 名五歲以下兒童死亡，占五歲以下兒童死亡人數的15%，肺炎是全世界兒童因感染導致死亡的主要原因[1]。2019 年12 月份出現的新型冠狀病毒，更是短期內在全球范圍內傳播。根據世衛組織最新實時統計數據，截至歐洲中部夏令時間2020 年7 月5 日12 時59 分(北京時間7 月5 日18 時59 分)，全球累計新冠肺炎確診病例11 125 245 例，累計死亡病例528 204 例[2]。因為疫情而造成的人們生活不便和經濟損失更是無法計量，借助數學模型分析和研究傳染病的傳播機理，預測和評估傳染病的發展趨勢，一直是科技工作者一個研究熱點。

自然界中一些生物群體會區分明顯的生長階段，如幼年和成年階段。幼年階段沒有生育能力，成年階段具有生育能力。幼年階段可能更易得某種疾病，如手足口病、水痘和肺炎等，成年階段更易患白喉、淋病和梅毒等疾病。因而，研究具有階段結構的疾病傳播模型有著重要的實際意義，具有階段結構的傳染病模型已有一些研究結果[3–10]。文獻[3–4]討論了疾病僅在幼年個體間傳播的情形，文獻[5–10]討論疾病僅在成年個體間傳播的情形。上述文獻多以常數或指數形式表達出生率，文獻[7–8]討論了具有飽和性的Beverton-Holt 出生函數和一般出生率函數，但是都沒有考慮患病個體也具有一定生育率的情況。文獻[10]研究了指數形式的出生率且患病個體具有一定出生率的傳染病模型。文獻[11]考慮了染病者具有自我恢復的階段結構傳染病模型。同時，后向分支的出現使得傳染病的控制出現了新的問題，也就是即使疾病的基本再生數小于1，系統也可能存在穩定的地方病平衡點[10–13]，討論后向分支出現的條件變得尤為重要。

在現有的具有階段結構的模型中，考慮成年個體的生長具有密度制約的文獻并不太多。本文在文獻[7,10]的基礎上，建立幼年以Beverton-Holt 函數形式出生、成年個體的生長受到密度制約、疾病僅在成年個體間傳播的傳染病模型，且患病成年個體具有一定的生育能力，分析了模型平衡點的穩定性和模型出現后向分支的條件，并討論患病個體生育對疾病控制帶來的影響。

1 模型建立

把群體分成幼年種群(x(t))和成年種群(y(t))兩個階段，幼年種群不感染疾病，成年種群感染疾病。出生率服從Berverton-Holt 函數，b(b> 0)為生育率系數，σ(σ ≥0)是疾病對出生率的影響系數，m(m ≥0)為決定出生率的飽和水平的常數，di(di> 0,i=1,2,3)表示幼年、健康成年和患病成年群體的自然死亡率，μ(μ> 0)是幼年個體的成熟率系數，δ(δ> 0)和η(η> 0)分別表示健康成年和患病成年群體的密度制約系數，k(k>0)表示傳染率系數。我們的模型以ODE 模型給出

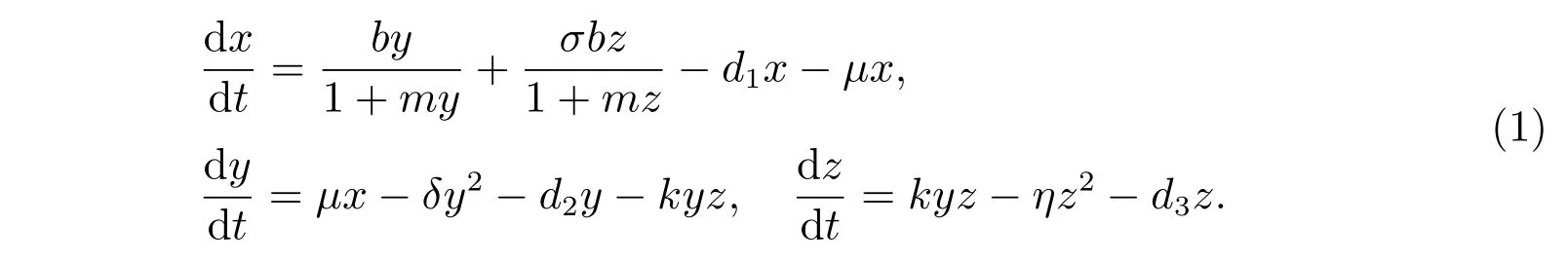
在本文中，如果令m= 0，則模型退化為文獻[10]中的模型。如果σ= 0，則模型退化為文獻[7]中的模型，所以本文是對前人研究成果的推廣和擴展。

顯然，給定初值(x(0),y(0),z(0))∈，其中={(x,y,z)|x ≥0,y ≥0,z ≥0}。模型(1)在有唯一全局解，且解會一直在。為了后面討論方便，我們定義兩個閾值參數

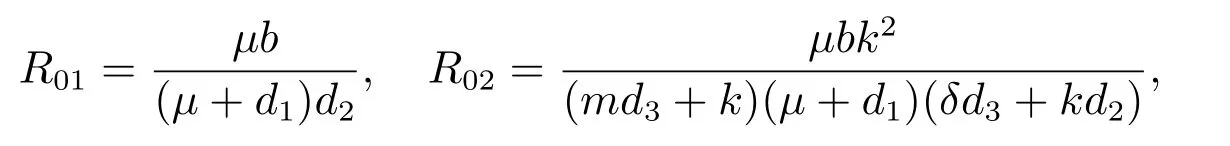
顯然R01>R02。

下面討論系統平衡點的存在性和穩定性。

2 平衡點的存在性和穩定性

定理1對于模型(1)，系統總存在絕滅平衡點E0(0,0,0)。當R01>1 時，模型(1)有系統存活無病平衡點E1(x1,y1,0)，其中

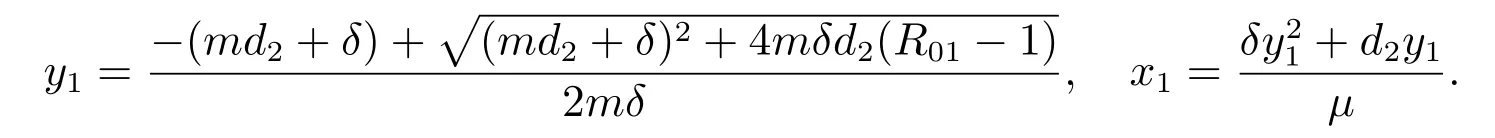
證明 模型(1)的平衡點由下面方程組的解給出

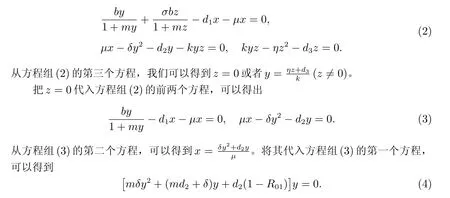
方程(4)總有解y=0，由此可以得到絕滅平衡點E0。當R01>1 時，方程(4)有唯一正解，且

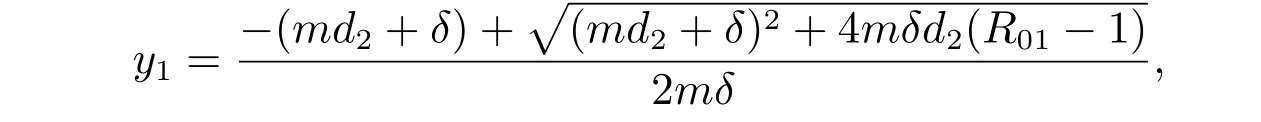
可以得到系統存活無病平衡點E1。

記

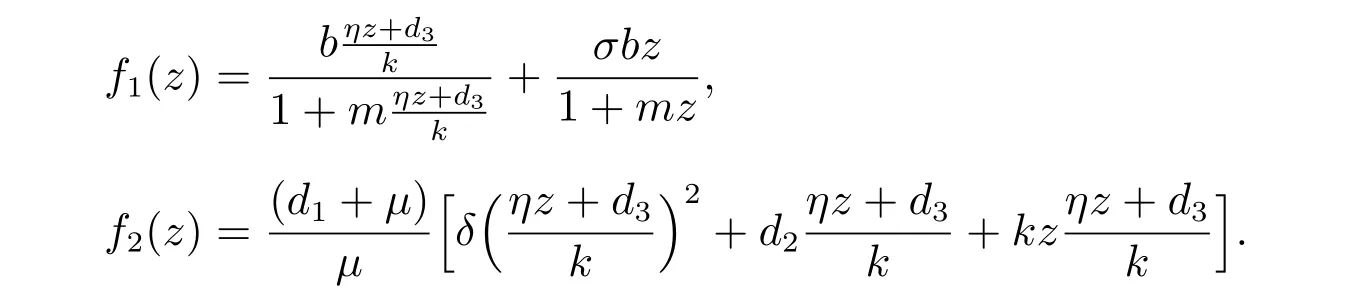
定理2對于模型(1)，下面結論成立：

對f1(z)和f2(z)求導，可得

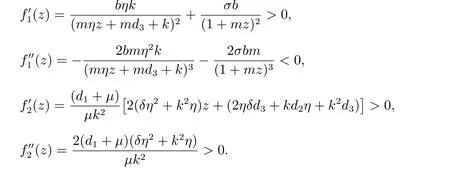
顯然f1(z)在第一象限是凸增曲線，且當z →+∞時，收斂于(1+σ)。f2(z)在第一象限凹增曲線，且當z →+∞時，趨于+∞。

(i) 當f1(0)>f2(0)，即就是

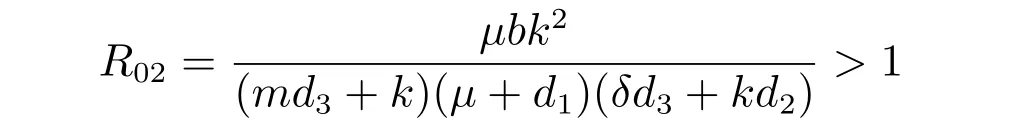
時，f1(z)和f2(z)在第一象限有唯一交點，也就是方程(6)有唯一正解z?，模型(1)有唯一正平衡點E?(x?,y?,z?)。

定理3對模型(1)，具有以下結論：

證明 在平衡點E0的特征方程為

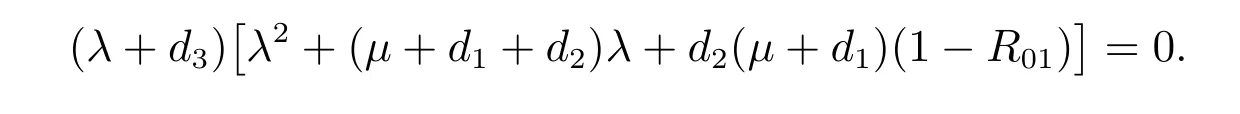
顯然，λ=?d3是一個特征根，另外兩個特征根由一元二次方程

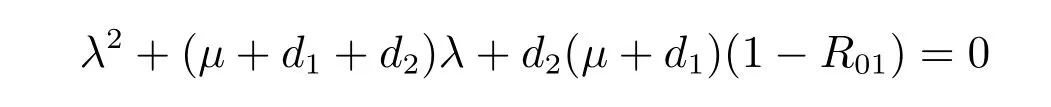
決定，由韋達定理知，當R01＜ 1 時，一元二次方程兩個根都是負的；當R01> 1 時，一元二次方程兩個根一正一負。所以，當R01＜1 時，模型的系統絕滅平衡點E0在上是局部漸近穩定的；當R01>1 時，E0是不穩定的。

在平衡點E1的特征方程為

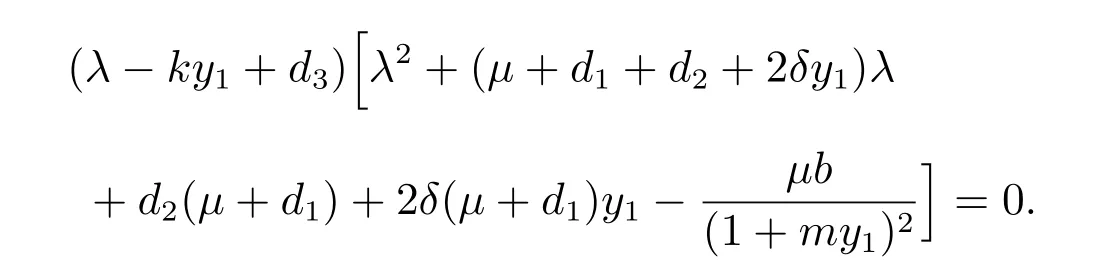
顯然，λ=ky1?d3是一個特征根，另外兩個特征根由一元二次方程

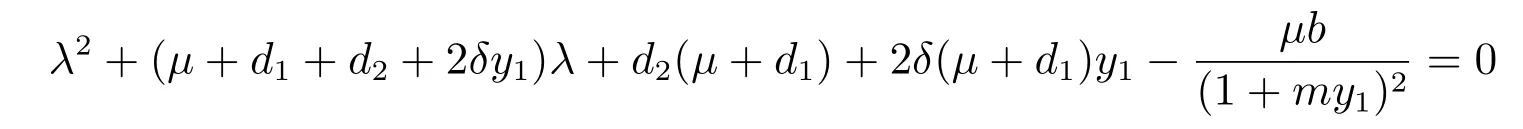
決定，且有

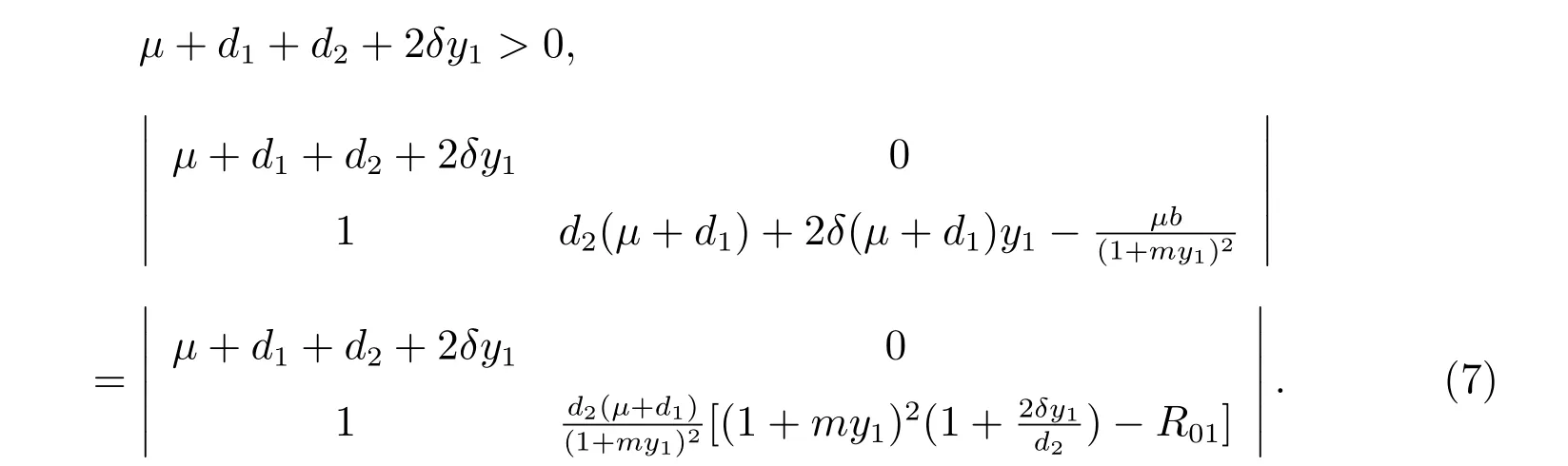
當

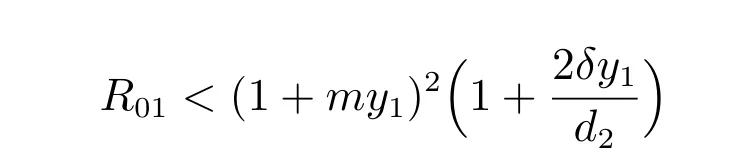
時，方程(7)大于零。由Routh-Hurwitz 判據知，當

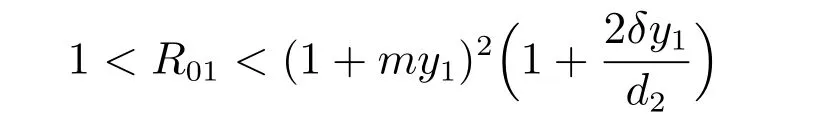
且ky1d3時，系統存活無病平衡點E1在{(x,y,z)|(x,y,z)∈且(x,y,z)?=(0,0,0)}上是局部漸近穩定的。

定理4對模型(1)，以下結論成立：

(i) 當R01＜ 1 且σμb＜ (μ+d1)d3時，模型的絕滅平衡點E0在上是全局漸近穩定的；

(ii) 當

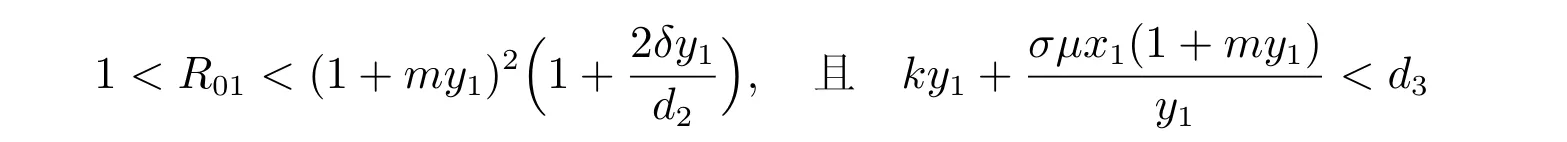
時，模型的存活無病平衡點E1(x1,y1,0)在{(x,y,z)|(x,y,z)∈且(x,y,z)?=(0,0,0)}上是全局漸近穩定的。

證明 (i) 定義Lyapunov 函數V1=μx+(μ+d1)(y+z)，則V1沿模型(1)的解的導數為

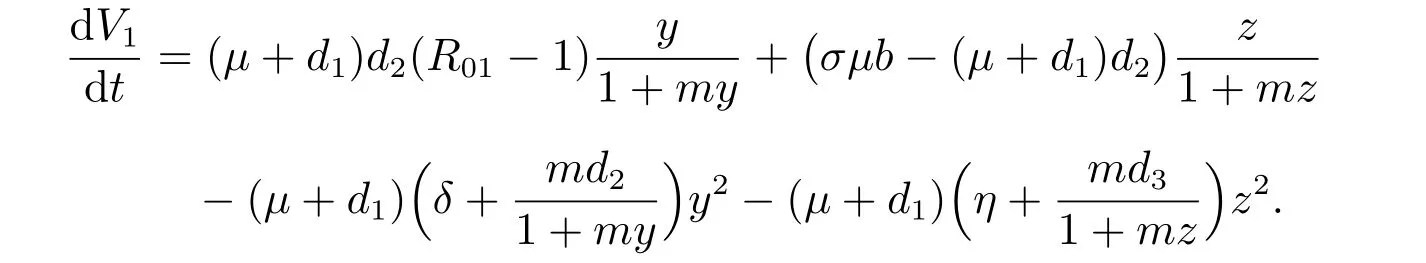
當R01＜1 且σμb＜(μ+d1)d3時，有dV1/dt ≤0。

dV1/dt= 0，當且僅當y=z= 0 時，顯然模型(1)在{(x,y,z)∈|dV1/dt=0}上的最大不變集是單點集E0。這樣，由LaSalle’s 不變集原理[14]知，平衡點E0在上是全局漸近穩定。

(ii) 下面討論系統存活無病平衡點E1的全局漸近穩定性。

定義Lyapunov 函數

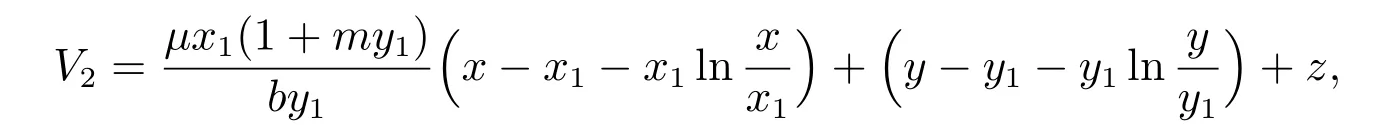
則V2沿模型(1)解的導數為

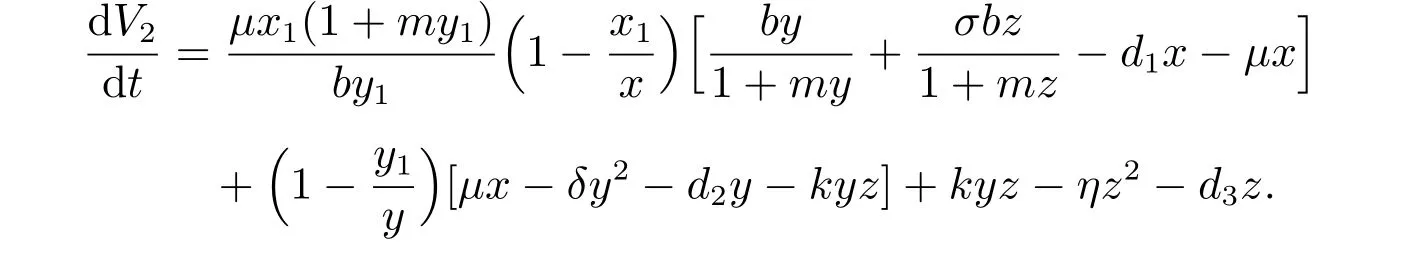
用等式

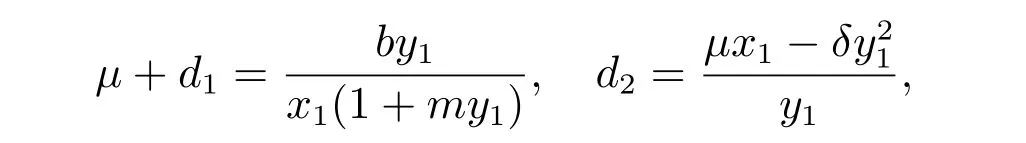
把dV2/dt重新寫為

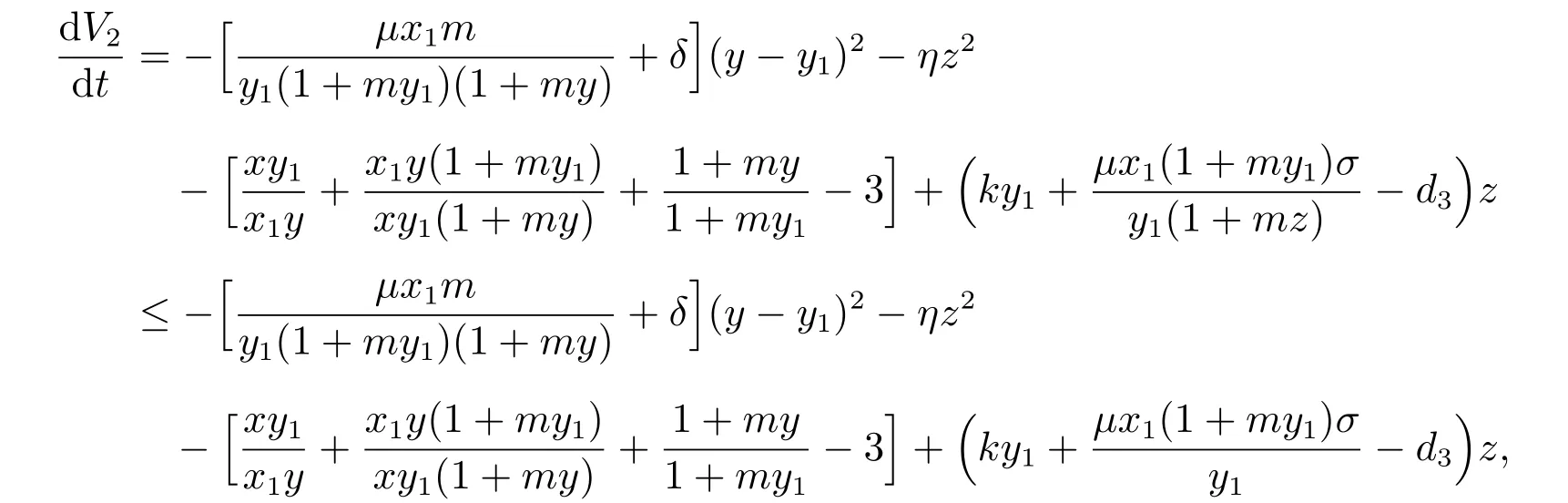
則當

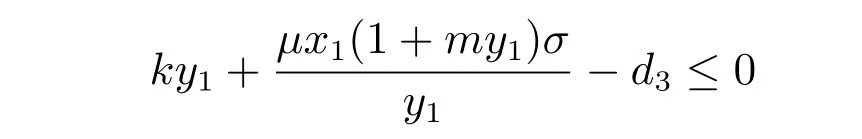
時，有dV2/dt ≤0，dV2/dt=0，當且僅當(x,y,z)=(x1,y1,0)。由Lyapunov 漸近穩定原理[14]，存活無病平衡點E1在{(x,y,z)|(x,y,z)∈且(x,y,z)?= (0,0,0)}上是全局漸近穩定的。

3 數值模擬

關于正平衡點的存在性，我們做了數值模擬如圖1。取參數b變化來模擬各種情況，在圖1 的(a)～(d)中分別取b=40,b=34.1,b=29.835 和b=32。其他參數如下

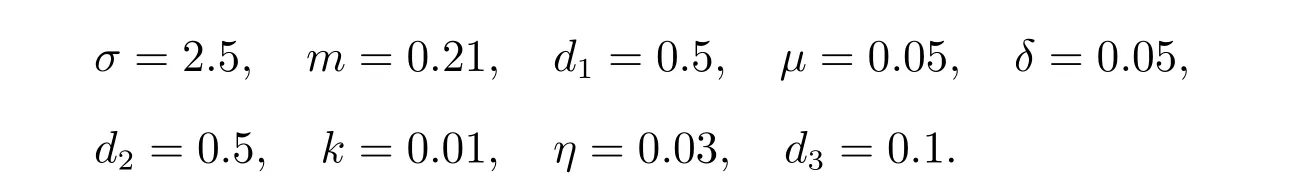
圖1 的(a)～(d)分別對應定理2 的(i)～(iv)正平衡點存在的四種情況。在圖1(a)中，正平衡點z?= 3.582 4，在圖1(b)中，正平衡點= 2.440 0，在圖1(c)中，正平衡點=0.888 0，在圖1(d)中，兩個正平衡點分別是z(1)=0.194 4,z(2)=1.914 8。

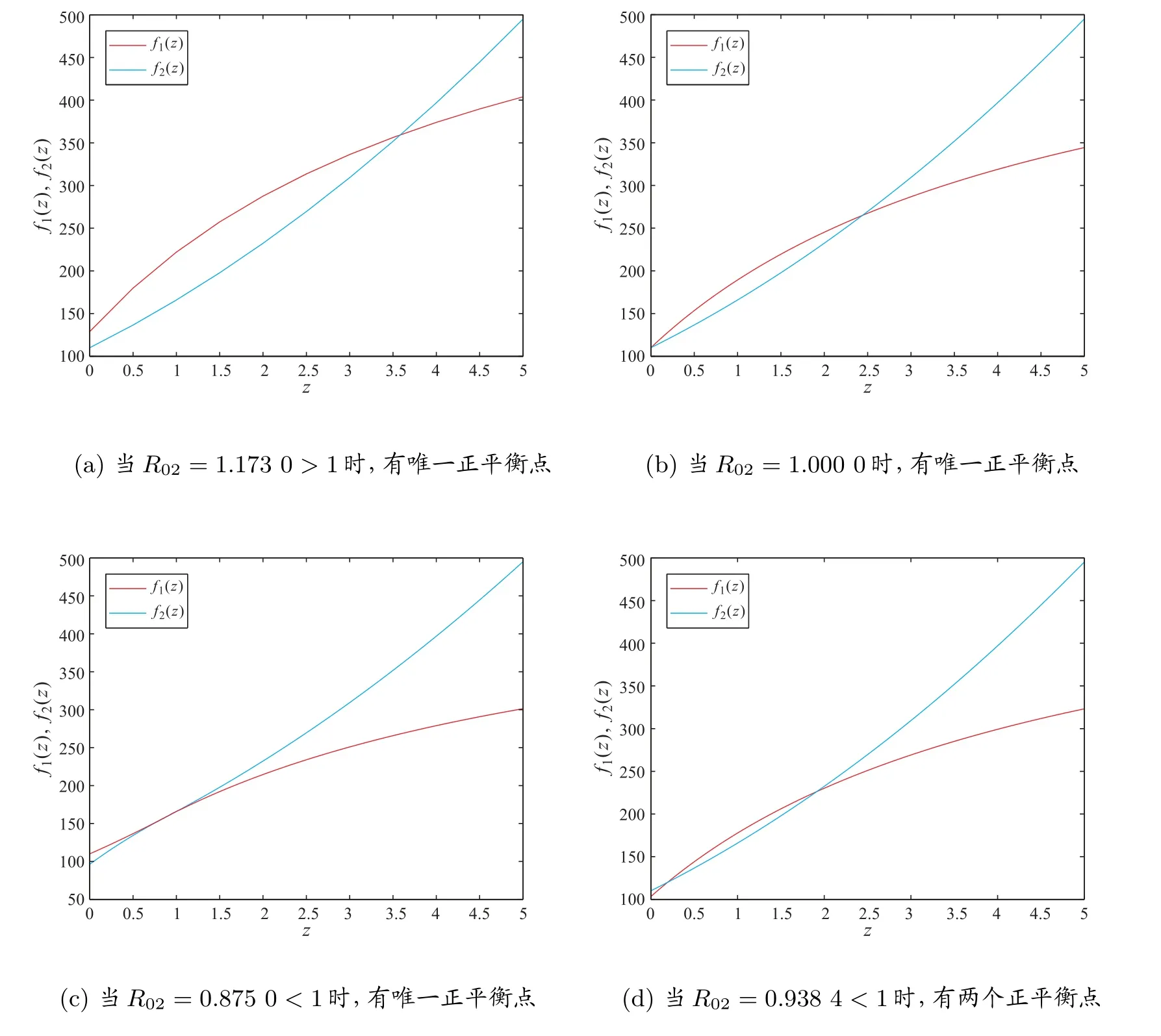
圖1 正平衡點的存在性

下面，我們應用軟件MatCont 做數值模擬來看平衡點的后向分支和前向分支，我們以閾值參數R02作為分支參數。b隨著R02變化，R02∈[0.8,1.9]，其他參數取值同圖1。從圖2(a)可以看出，取參數σ=2.5，此時

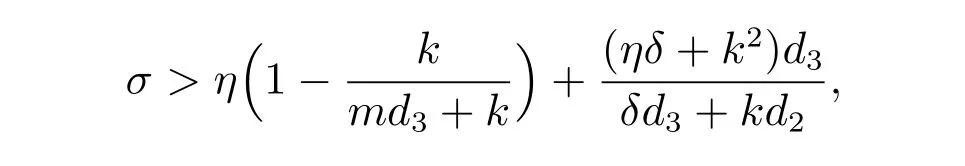
模型出現后向分支，可以看出R02= 1 為分支點BP，R02= 0.875 0 是臨界點LP。從圖2(b)可以看出，取參數σ=0.03，此時

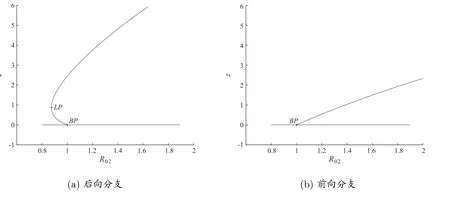
圖2 正平衡點分支

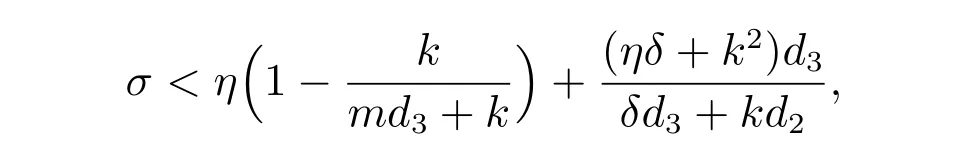
模型出現前向分支。

我們猜測R02> 1 時，唯一正平衡點是全局漸近穩定的，做了一些數值模擬也顯示正平衡點是全局漸近穩定的。取參數同圖1(a)，此時R02= 1.173 0> 1，正平衡點是全局穩定性，見圖3(a)。而當我們取參數同圖1(d)，R02= 0.938 4＜ 1，系統有兩個正平衡點。此時，數值模擬顯示一個正平衡點是局部穩定的，一個無病平衡點是局部穩定的，見圖3(b)。

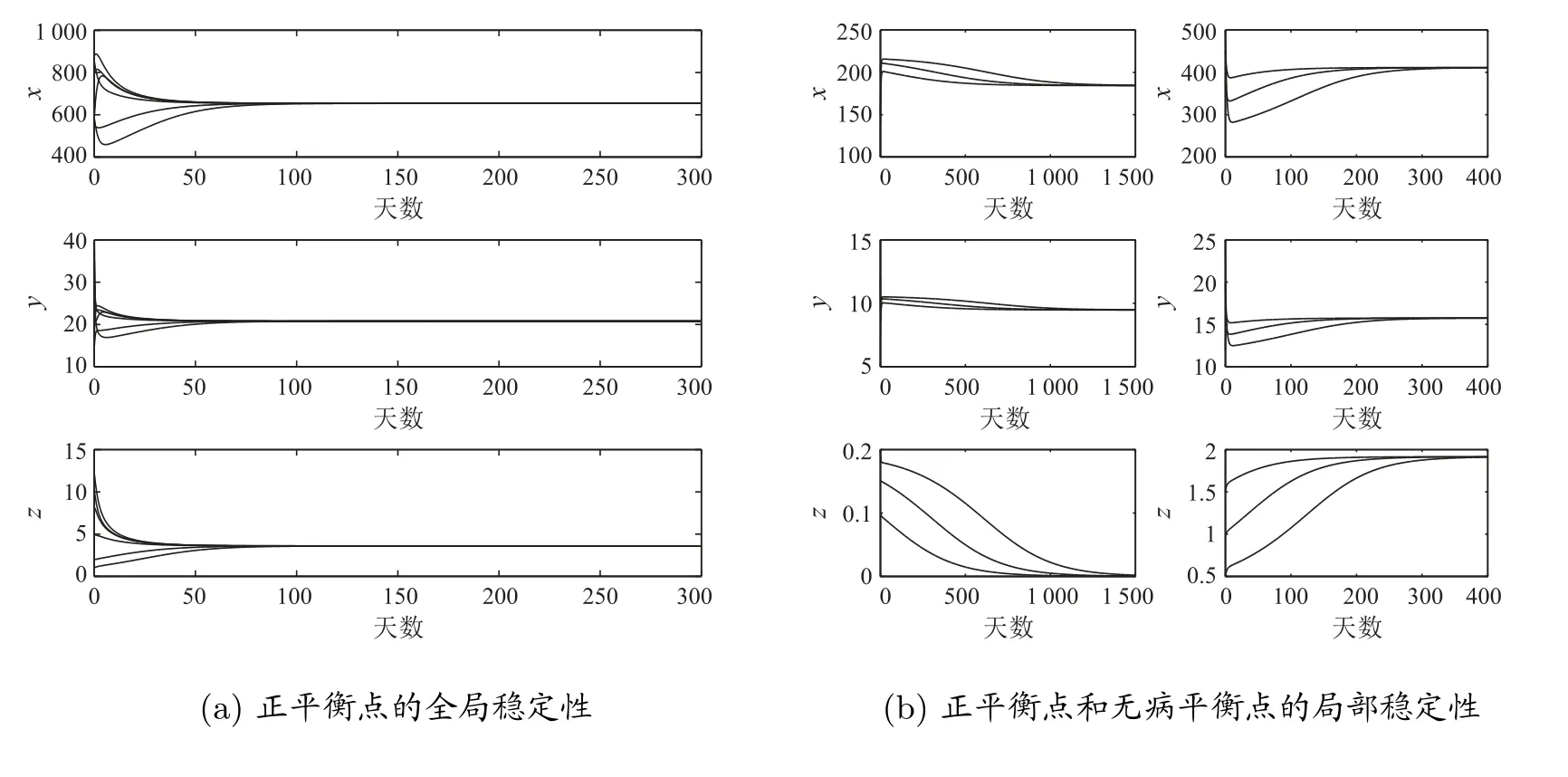
圖3 平衡點的穩定性

4 結論

本文建立了一個染病期也具有Bervent-Holt 生育率的階段結構傳染病模型，通過對模型的理論分析，得到了平衡點的存在性和穩定性，并且得到了系統絕滅的閾值參數R01和基本再生數R02。在本文中，我們研究了平衡點分支，得到了前向分支和后向分支發生的條件。

可以看出后向分支是由于染病期具有生育率的而引起的，當

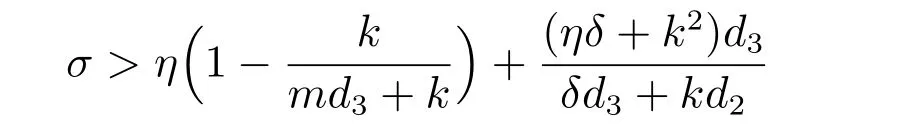
時，R02= 1 不再是疾病持續與否的閾值，R02＜ 1 時，疾病也會局部范圍內流行。Beverton-Holt 出生函數也對后向分支的出現有一定的作用，出生率的飽和水平常數m變小更可能出現后向分支。后向分支的出現是不利于疾病控制的，可以通過人為干預、媒體宣傳等手段使得患病群體在病愈之前不生育，從而降低σ到閾值以下，以達到控制疾病的目的。

關于R02>1 時，唯一正平衡點的全局穩定性，我們嘗試了構造類型

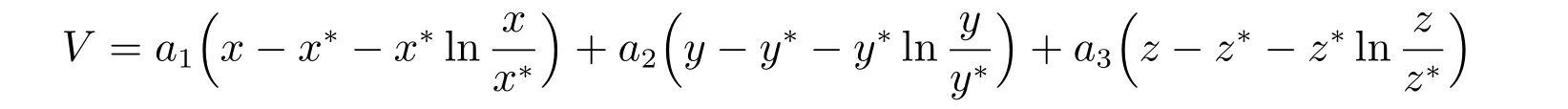
的V函數，沒有成功。構造V函數本身就是一個難點，也許可以構造其他類型的V函數，或者采用其他證明正平衡點全局穩定性的方法，我們把這個問題留作以后再解決。