M 矩陣的線性互補問題的誤差界

房喜明

(肇慶學院數學與統計學院，肇慶 526000)

0 引言

線性互補問題產生于一些科學計算，以及工程和經濟領域的應用，包括線性和二次規劃問題、彈性接觸問題、滑動軸承的自由邊界問題以及市場平衡問題等[1–4]。線性互補問題的數學模型為：尋找x ∈Rn，滿足條件

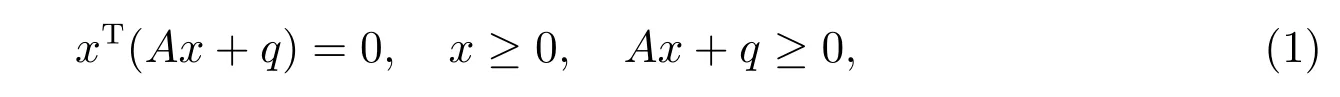
其中A ∈Rn×n,q ∈Rn為已知。線性互補問題通常簡記為LCP(A,q)。

對于線性互補問題LCP(A,q)，近幾十年來，無論是在理論方面還是在數值求解方面，許多學者一直在研究，取得了豐富的理論成果。理論研究包括解的存在性、唯一性、穩定性，以及線性互補問題LCP(A,q)與其他問題的聯系[5–10]。線性互補問題的一個著名的結論是：線性互補問題LCP(A,q)對于任意q ∈Rn存在唯一解的充分必要條件是A為P矩陣。關于P矩陣，它包括許多特殊類型，如正定矩陣和H+矩陣等[2,11–12]。Mathias 和Pang 在文獻[5]中引入一個關于P矩陣的函數c(A)，并對c(A)的值給出一些估計。Cottle 等在文獻[6]中，使用函數c(A)提出關于線性互補問題擾動的一些結論。由于函數c(A)不容易計算，許多學者探討使用其他函數來估計誤差界，處理系數矩陣為特殊矩陣，如H+矩陣和B矩陣等的線性互補問題[9,12–17]。Chen 和Xiang 在文獻[7]中基于矩陣函數αp(A)討論了線性互補問題的誤差界。函數αp(A)后來被一些學者使用，且在估計誤差界等方面表現比較好。αp(A)也存在不容易計算問題。因此，它的估計值常被使用[12–13,16]。有關線性互補問題LCP(A,q)的其他理論和數值解法，參見文獻[2,8,11]。

本文使用函數αp(A)進一步研究線性互補問題LCP(A,q)的誤差界。首先，給出函數αp(A)的準確值，其中A是一個主對角元為1 的M矩陣。之后，給出該類M矩陣的線性互補問題LCP(A,q)的絕對誤差界和相對誤差界。接下來，通過等價轉化將誤差界理論推廣到一般情形，即給出系數矩陣為一般M矩陣的線性互補問題的誤差界。最后，給出一些與誤差界有關的數值試驗。本文給出函數αp(A)的準確值，并將該函數應用到估計線性互補問題LCP(A,q)的誤差界。主要結論見定理1 至定理6。數值結果表明，由αp(A)的準確值得出的誤差界理論比現有一些理論好。

本文結構安排如下：第1 部分簡要介紹一些定義和基本結論等；第2 部分給出本文的主要結果；第3 部分給出一些數值例子；第4 部分是結束語。

1 準備知識

在這部分，我們簡要介紹本文中所涉及的一些概念、符號和基本結論等。

定義1[7]矩陣A=(aij)∈Rn×n稱為M矩陣(在一些文章中稱為非奇異M矩陣)，如果A滿足

定義2[2]矩陣A=(aij)∈Rn×n稱為H+矩陣，如果A滿足aii>0(i=1,2,···,n)，且其比較矩陣〈A〉=(〈aij〉) 為M矩陣，其中〈aij〉定義為

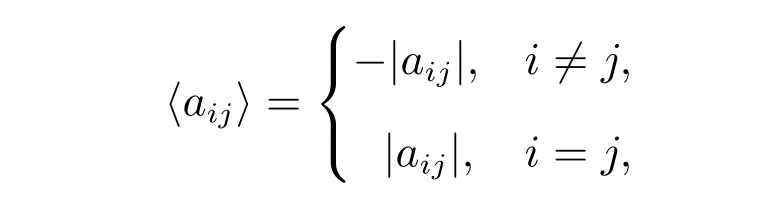
其中“|·|”表示絕對值函數。

對于P矩陣A，函數c(A)定義為

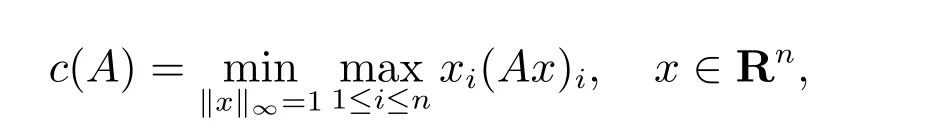
詳細資料可參考文獻[5]。對于任意向量x,y,x?,y?∈Rn，根據文獻[7]，有如下關系式

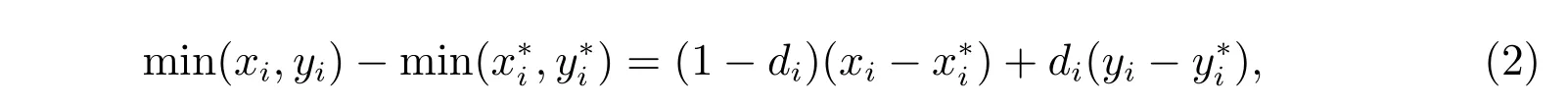
其中di ∈[0,1](i=1,2,···,n)。基于式(2)，Chen 和Xiang 在文獻[7]中給出線性互補問題的絕對誤差界，即

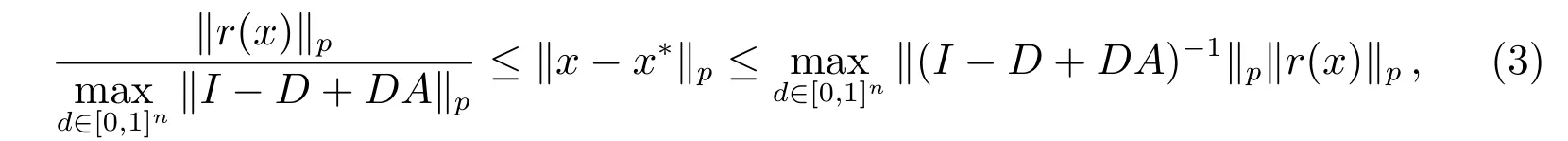
其中p ≥1 或p=∞，x?,x ∈Rn分別表示線性互補問題LCP(A,q)的解和任意實向量。D= diag(d) = diag([d1d2··· dn])是一個對角矩陣，其對角元di滿足di ∈[0,1](i=1,2,···,n)。線性互補問題LCP(A,q)的自然余量函數r(x)定義為

其中min 表示兩實向量依分量取最小。

引理1[7]假定A ∈Rn×n是一個H+矩陣，則

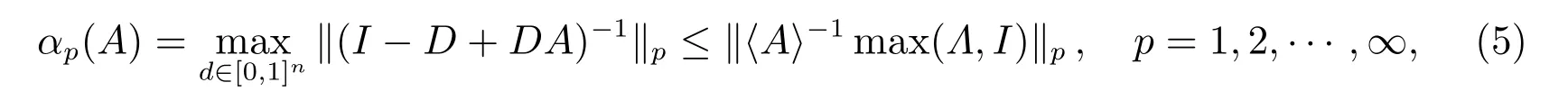
其中〈A〉和Λ分別表示矩陣A的比較矩陣和主對角矩陣，矩陣max(Λ,I)定義為

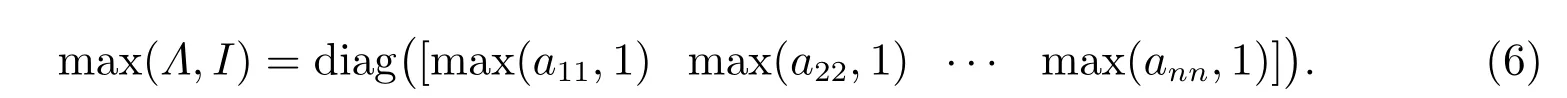
引理2[13]假定A ∈Rn×n是一個M矩陣，則

2 主要結果

在這部分，我們首先給出主對角元滿足aii= 1(i= 1,2,···,n)的M矩陣A的矩陣函數αp(A)的準確值，之后，使用該函數估計線性互補問題LCP(A,q)的誤差界，并給出一些結論。

定理1如果A ∈Rn×n是一個M矩陣，且滿足aii=1(i=1,2,···,n)，則

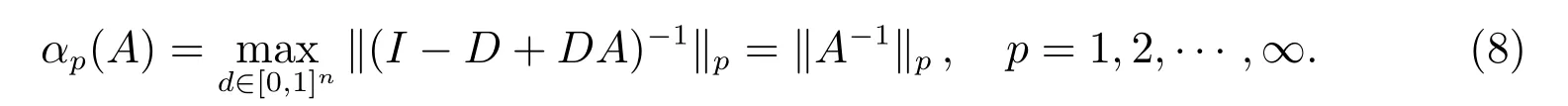
證明 因為A是一個M矩陣，所以A是一個H+矩陣，且滿足〈A〉=A。結合引理1 和已知條件aii=1(i=1,2,···,n)，有

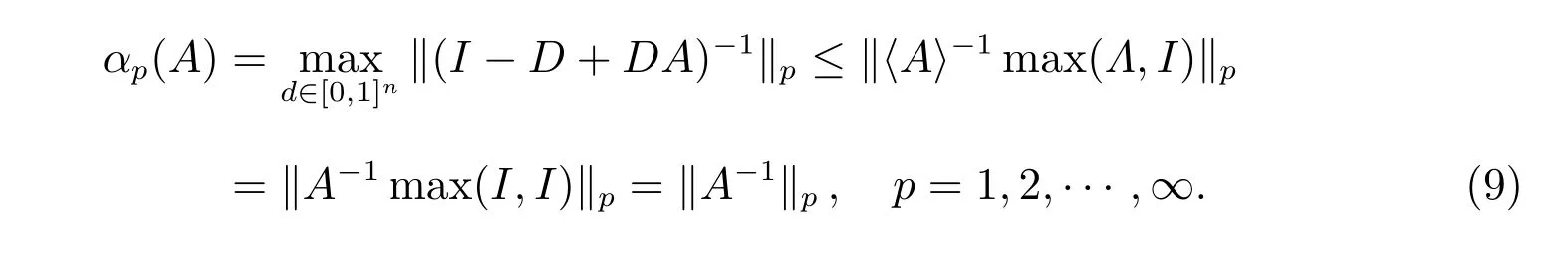
與此同時，由引理2，可得

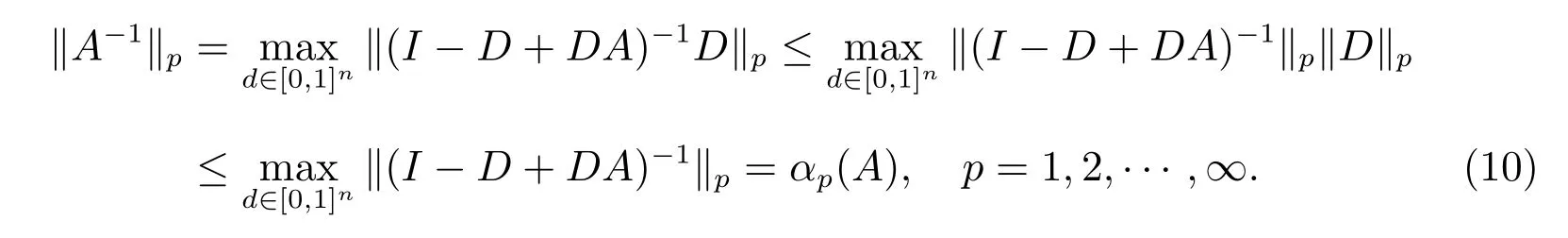
因此，根據式(9)和式(10)，可知等式(8)成立。

注1在文獻[7]中，作者討論函數α1(A)，并給出一個計算公式，即α1(A) =maxv∈V f(v)，其中容易看出，該公式不便于實際使用。定理1 給出函數αp(A)，當p=1,2,···,∞時的準確值，改進了文獻[7]的結果。

引理3如果A ∈Rn×n是一個M矩陣，并且滿足aii=1(i=1,2,···,n)，則

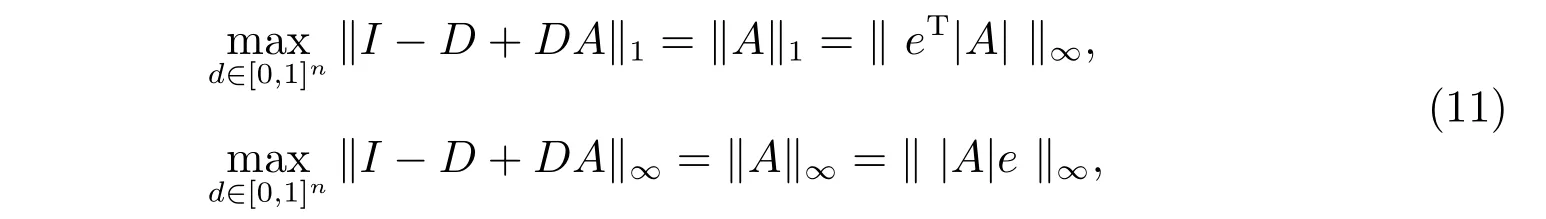
其中e=(1,1,···,1)T，|A|=(|aij|)表示矩陣A的絕對值矩陣。

證明 因為

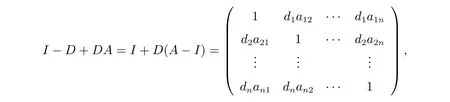
其中di ∈[0,1](i= 1,2,···,n)。根據矩陣范數//· //1和//· //∞的定義，容易證得公式(11)中的兩個等式成立。

根據定理1 和引理3，不等式(3)中的絕對誤差界可以表示成更精確形式，即下面的定理。

定理2如果A ∈Rn×n是一個M矩陣，且滿足aii= 1(i= 1,2,···,n)，向量x?∈Rn是線性互補問題LCP(A,q)的解，則對于任意向量x ∈Rn，不等式

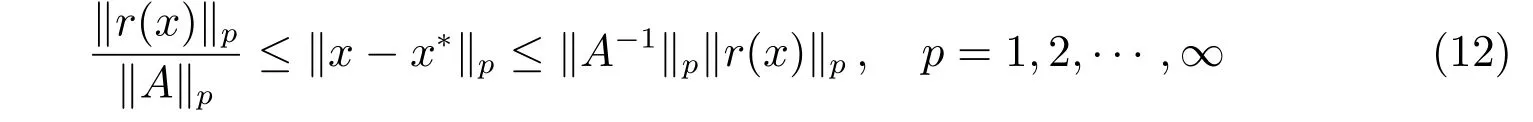
成立，其中r(x)由式(4)給出。

證明 根據定理1 和引理3，可知

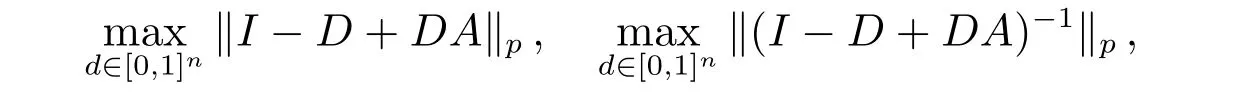
分別滿足

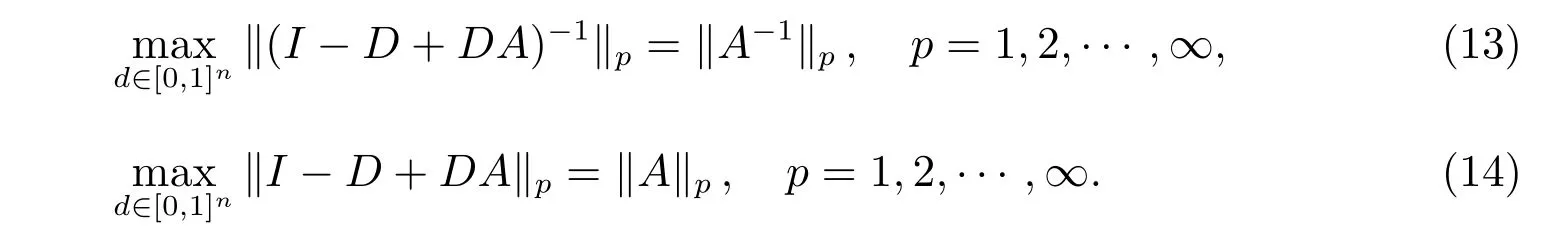
因此，在不等式(3)中使用式(13)和式(14)進行替換，易得式(12)成立。

推論1如果A ∈Rn×n是一個M矩陣，且滿足aii= 1(i= 1,2,···,n)，向量x?∈Rn是線性互補問題LCP(A,q)的解，則不等式

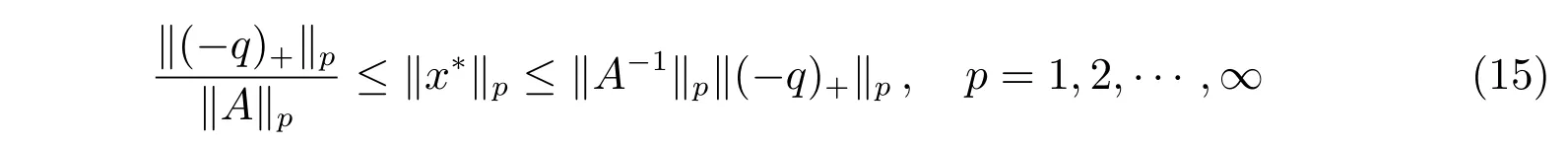
成立，其中(?q)+=max(0,?q)。

證明 由式(4)，可得

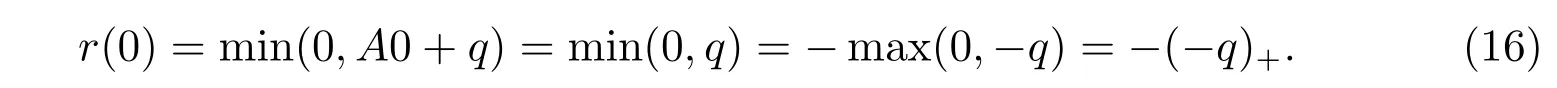
在式(12)中取x=0，結合式(16)，易證不等式(15)成立。

一方面，我們得到//x ?x?//p的界，即定理2 中的式(12)。另一方面，我們得到//x?//p的界，即推論1 中的式(15)。因此，易得下關于相對誤差界的結論。

定理3如果A ∈Rn×n是一個M矩陣，且滿足aii= 1(i= 1,2,···,n)，向量x?∈Rn是線性互補問題LCP(A,q)的解，則對于任意x ∈Rn，如果(?q)+?=0，不等式

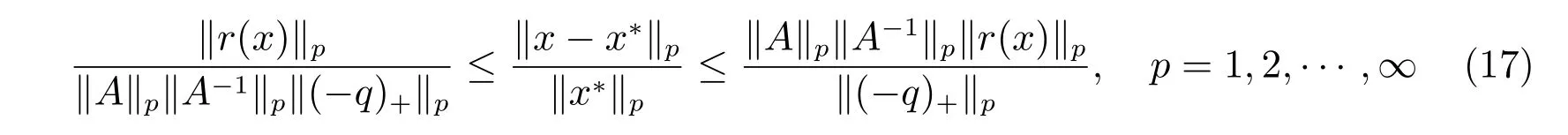
成立，其中r(x)由式(4)給出，(?q)+=max(0,?q)。

注2定理2、推論1 和定理3 顯示，如果A ∈Rn×n是一個M矩陣，且滿足aii=1(i=1,2,···,n)，則：

接下來，我們考慮一般情形，即線性互補問題LCP(A,q)的系數矩陣A為普通的M矩陣，也即A的主對角矩陣不一定是單位矩陣。首先，給出一個基本結論，即對于任意的正對角矩陣Λ，有等價關系

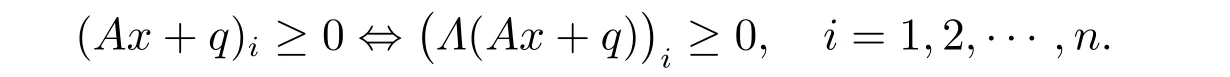
根據M矩陣的理論，線性互補問題LCP(A,q)的定義以及上面的等價關系，容易證得下面的引理。

引理4如果A ∈Rn×n是一個M矩陣，則對于任意的正對角矩陣Λ，矩陣ΛA也是M矩陣。

引理5如果A ∈Rn×n是一個M矩陣，則對于任意的正對角矩陣Λ，線性互補問題LCP(A,q)等價于線性互補問題

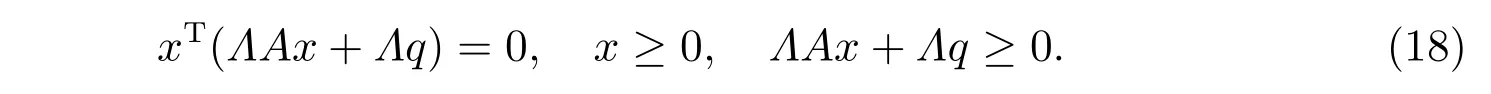
引理4和引理5 的證明過程省略。如果記線性互補問題(18)為LCP(ΛA,Λq)，則引理5 可以概況為：對于任意的正對角矩陣Λ，線性互補問題LCP(A,q)等價于線性互補問題LCP(ΛA,Λq)。因為M矩陣的主對角矩陣是正對角矩陣，結合引理4、引理5 以及定理1 至定理3，可得下面一些結論。

定理4如果A ∈Rn×n是一個M矩陣，其主對角矩陣為Λ，向量x?∈Rn是線性互補問題LCP(A,q)的解，則對于任意的x ∈Rn，不等式

成立，其中rΛ?1(x)=min(x,Λ?1Ax+Λ?1q)。

證明x?是系數矩陣為M矩陣的線性互補問題LCP(A,q)的解，也是線性互補問題LCP(Λ?1A,Λ?1q)的解。由于系數矩陣Λ?1A是一個M矩陣，且其主對角矩陣為單位陣，由定理2 可知，x和x?滿足式(12)，即

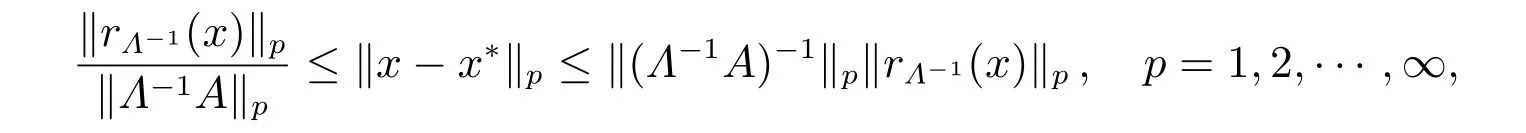
其中rΛ?1(x)由式(4)給出，即rΛ?1(x)=min(x,Λ?1Ax+Λ?1q)。因此，式(19)得證。

定理5如果A ∈Rn×n是一個M矩陣，其主對角矩陣為Λ，向量x?∈Rn是線性互補問題LCP(A,q)的解，則不等式

成立，其中(?Λ?1q)+=max(0,?Λ?1q)。

不等式(20)容易證明，只需在式(19)中取x= 0 即可。基于定理4 和定理5，與定理3 類似，可以得到系數矩陣為一般M矩陣的線性互補問題的相對誤差界。

定理6如果A ∈Rn×n是一個M矩陣，其主對角矩陣為Λ，向量x?∈Rn是線性互補問題LCP(A,q)的解，則對于任意x ∈Rn，如果(?q)+?=0，不等式

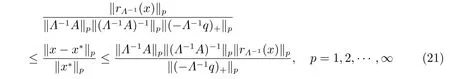
成立，其中

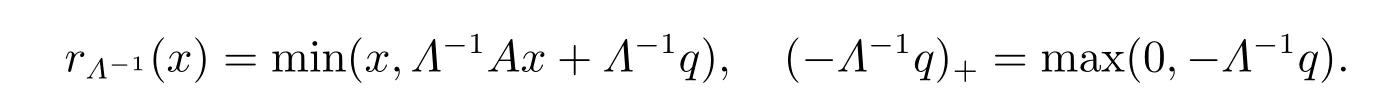
對于系數矩陣為M矩陣的線性互補問題LCP(A,q)，根據文獻[5]，有

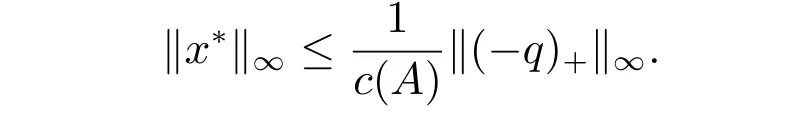
同時，根據推論1，有

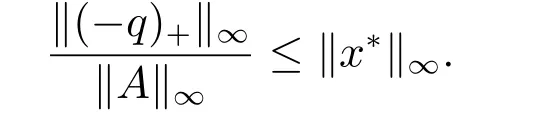
因此，有

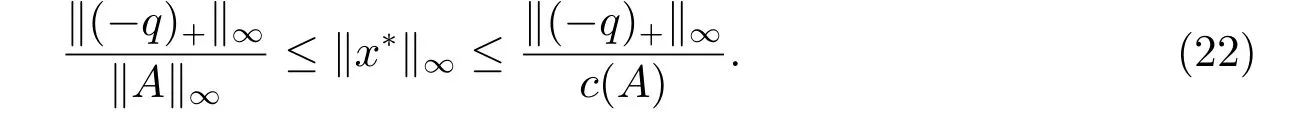
結合式(22)和定理5，可得x?新的界

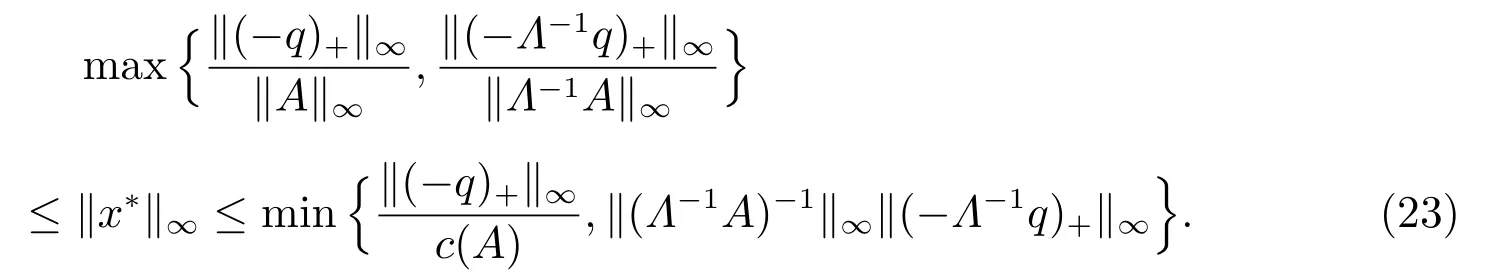
因此，如果記式(23)的左側和右側分別為Ul和Ur，可得新的相對誤差界

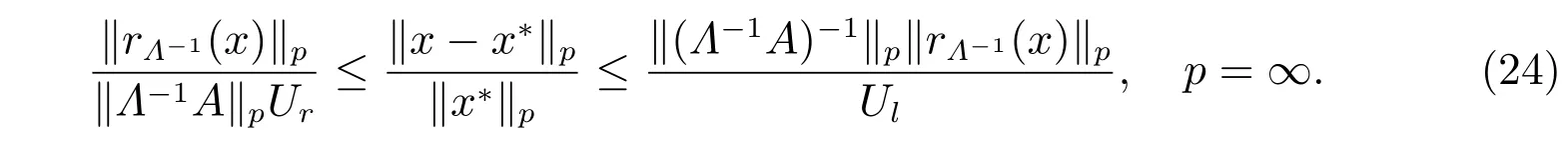
因為式(24)比式(21)更復雜，并且涉及不易計算的函數c(A)，本文不討論。

3 數值例子

在這部分，我們給出一些數值例子，并與已有結論進行比較。前3 個例子是低階線性互補問題，第4 個例子是高階線性互補問題。在第1 個例子中，我們將定理4 與文獻[7,12,16]中的結論進行數值比較。第2 個和第3 個例子分別關于準確解的界和數值解的誤差界。在最后的一個例子中，我們使用迭代法求解線性互補問題LCP(A,q)，并用定理4 估計每步所得數值解的誤差界。

例1在這個例子中，考慮數值解的絕對誤差界。選取線性互補問題LCP(A,q)中的系數矩陣A為

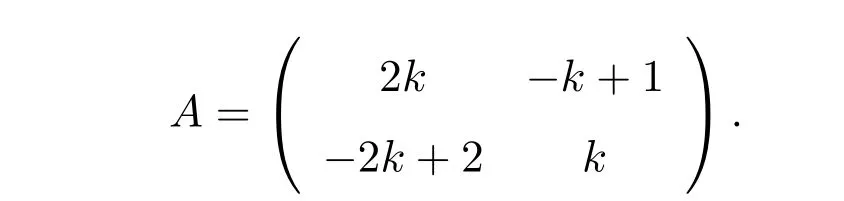
該矩陣是一個非對稱M矩陣，曾出現在文獻[12,16]中，其中k>1，則

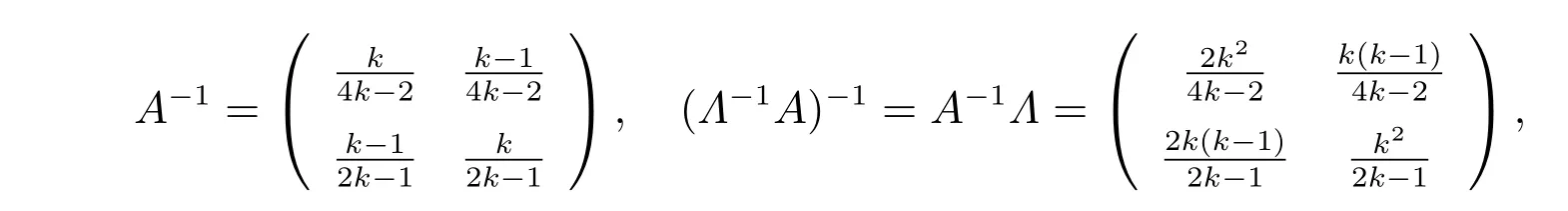
其中

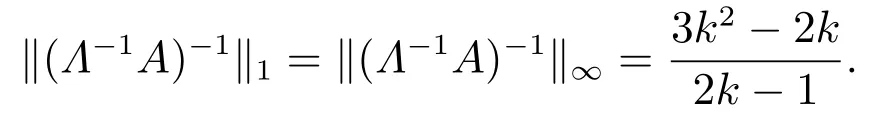
令q=(0,?ε)T,x=ε(1,2)T，則

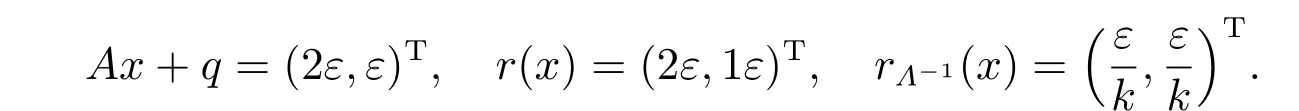
根據定理4，關于數值解x的誤差界，有

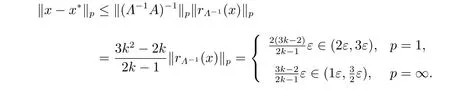
根據文獻[7]中的式(2.4)，有

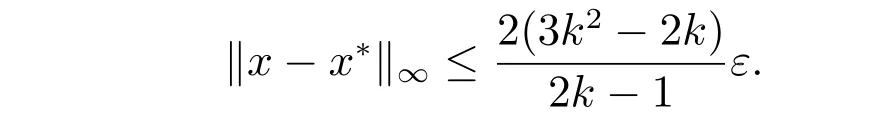
根據文獻[16]中的式(2.3)，有

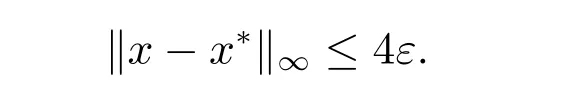
根據文獻[12]中的式(3.5)，有

例2在這個例子中，我們考慮線性互補問題真實解的界。在線性互補問題LCP(A,q)中，選取A和q分別為

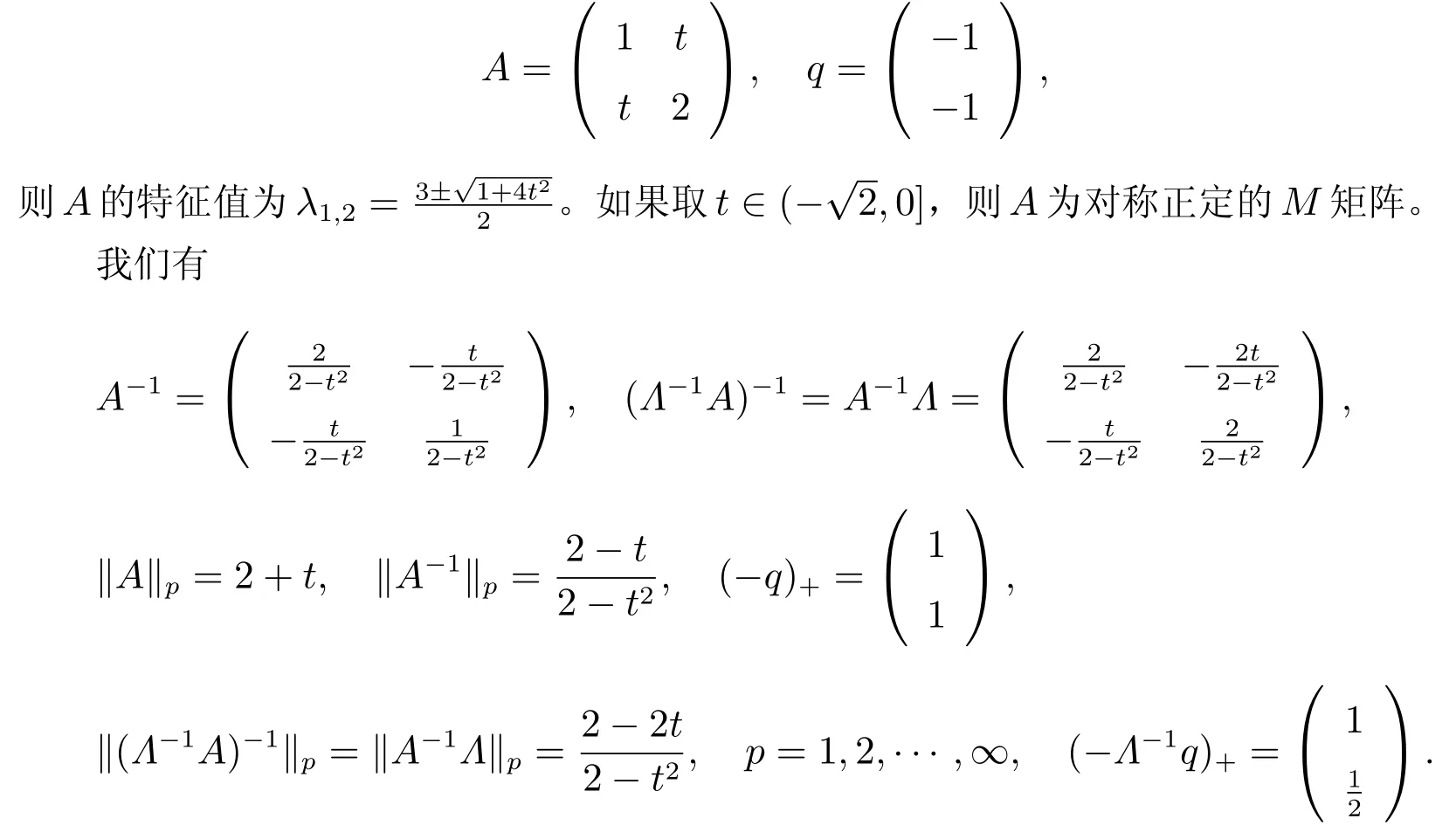
因此，可得線性互補問題LCP(A,q)的真實解x?的上界為

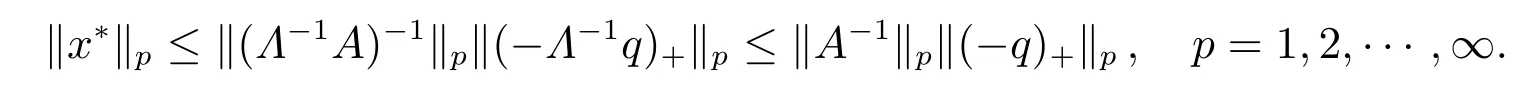
第一個不等式是根據定理5，第二個不等式是根據文獻[7]中的定理2.4。可以看出，兩個上界相等的一個條件是矩陣A為正對角矩陣，即t= 0，并且p=∞。因此，這個例子顯示，定理5 給出的上界比文獻[7]給出的上界好。

例3在這個例子中，我們考慮一個具體的線性互補問題，在LCP(A,q)中選取A和q分別為

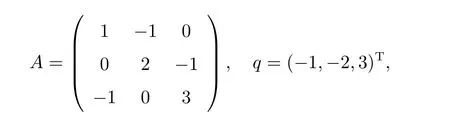
則A是一個非對稱的M矩陣，線性互補問題LCP(A,q)的準確解為x?=(2,1,0)T。假定數值解為x=(2.1,0.9,?0.1)T，則

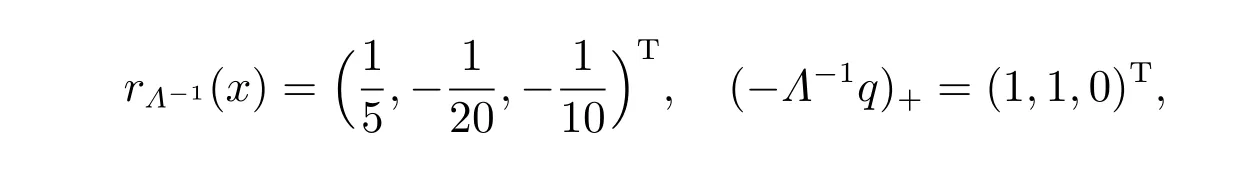
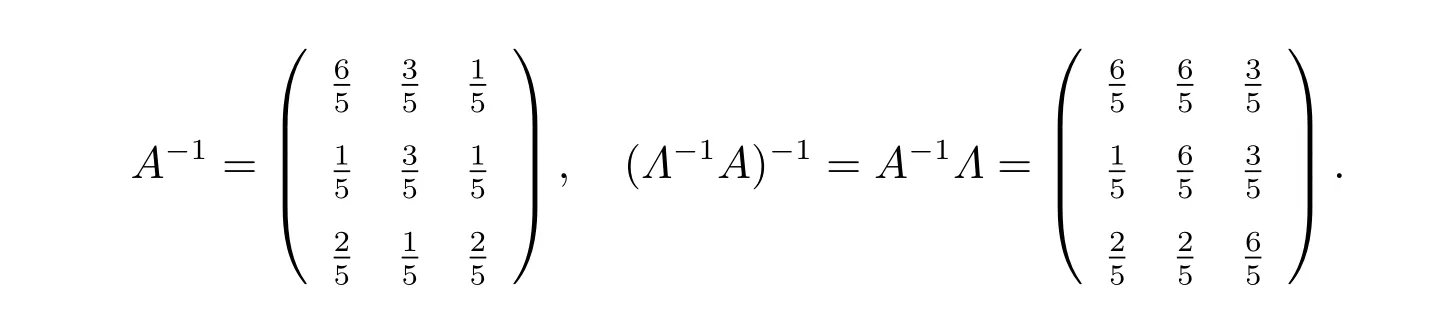
通過計算，可得表1 和表2。

表1 誤差界涉及的一些量

表2 絕對誤差界和相對誤差界

表1 給出誤差界涉及的一些量，表2 給出根據定理4 和定理6 計算得到的誤差界。從表2 可以看出，定理4 和定理6 給出的誤差界可以用來估計數值解與準確解之間的近似程度。從這個例子中也可以看出絕對誤差界比相對誤差界更接近真實情況。

例4在這個例子中，我們考慮一個高階的線性互補問題。數值解由Modulus-based Gauss-Seidel(MGS)迭代法計算得到，該方法是求解線性互補問題LCP(A,q)數值解的有效方法之一，詳細資料可參見文獻[2]。在LCP(A,q)中，選取A為一個塊三對角M矩陣，即A=Tridiag(?I,S,?I)+D ∈Rn×n，其中

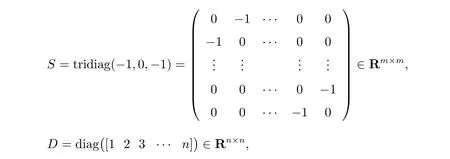
I是一個m階單位矩陣，其中n=m2。取準確解x?和q分別為x?= (1,2,1,2,···)T∈Rn,q=?Ax?。在MGS 迭代法中，選取參數矩陣?= diag(diag(A))，初始迭代向量x(0)為x(0)= (1,0,1,0,···)T∈Rn。設置停止迭代條件為norm(r(x(k)))＜ 10?5，其中x(k)表示k次迭代得到的數值解，符號“diag”和“norm”是數學軟件Matlab 中的兩個函數。考慮誤差//x(k)?x?//p的下界、上界和準確值，其中p= 1,2,···,∞。令n=900，得到下圖1 和圖2。

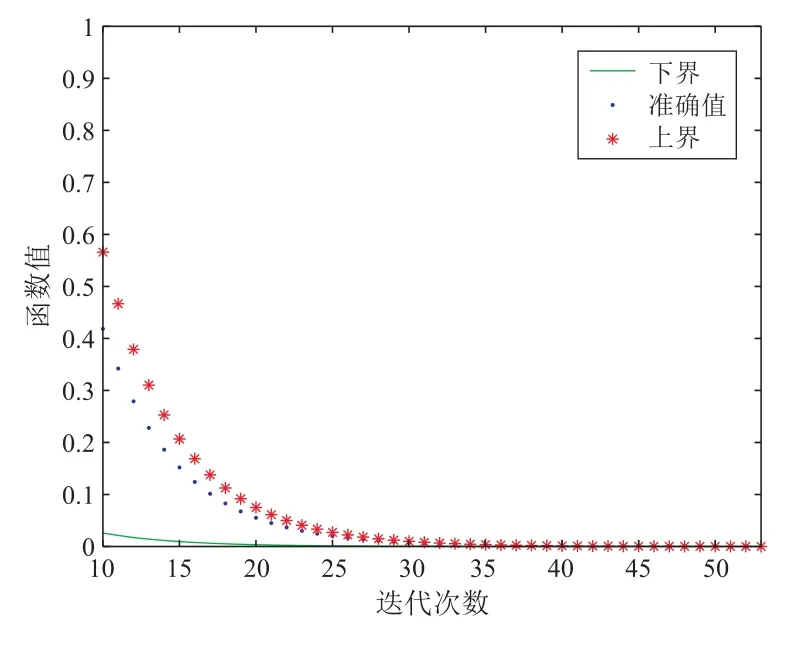
圖1 x(k)關于范數//·//1 的誤差界

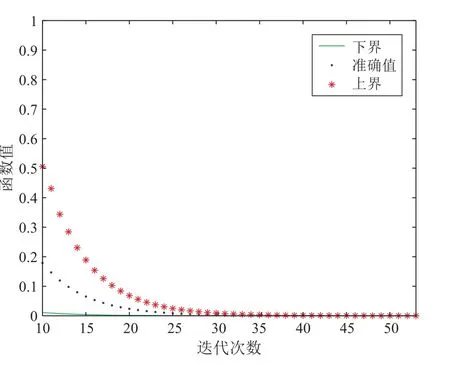
圖2 x(k)關于范數//·//∞的誤差界

在圖1 和圖2 中，水平軸表示迭代步數，圖中直線、點線和星線分別表示函數

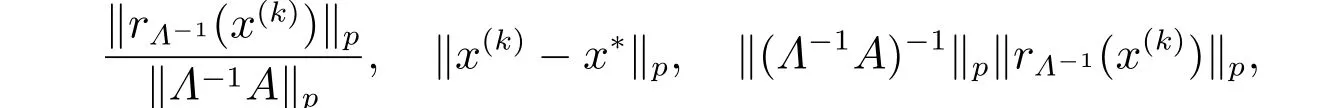
其中p=1,2,···,∞。數值結果表明，定理4 可以用來估計數值解的絕對誤差。

4 結束語

在本文中，基于矩陣函數αp(A)的準確值和線性互補問題LCP(A,q)的等價轉化，我們給出系數矩陣為M矩陣的線性互補問題的誤差界。數值結果表明，所給的誤差界是有效的和實用的。與相對誤差界比較，絕對誤差界與實際情況更接近一些。要更好地估計相對誤差界，需要探尋其他的理論和方法。同時，有關線性互補問題LCP(A,q)的擾動和求解方法等，也值得后續進一步探討。