借助中點(diǎn)精準(zhǔn)溯源，探究一題多解本質(zhì)

鮑利輝

（杭州師范大學(xué)東城中學(xué) 浙江杭州 310019）

作為從初中幾何學(xué)習(xí)初便涉及的知識(shí)點(diǎn)，“中點(diǎn)”有諸多相關(guān)知識(shí)點(diǎn)與衍生知識(shí)點(diǎn)，內(nèi)容體系相對(duì)復(fù)雜，因此學(xué)生在面對(duì)題目中此類條件時(shí)會(huì)顯得手足無(wú)措，無(wú)從入手.只有在整體視角下對(duì)這些知識(shí)點(diǎn)進(jìn)行梳理，結(jié)合具體的圖像，實(shí)現(xiàn)精準(zhǔn)溯源，才能真正理解與掌握中點(diǎn)相關(guān)的知識(shí)網(wǎng)絡(luò)，從而達(dá)到一題多解。

一、知識(shí)溯源分析法的意義

在平常教學(xué)過(guò)程中，經(jīng)常存在解法單一的情況，究其根源與忽視對(duì)多解生成本源的思考有關(guān)。就數(shù)學(xué)轉(zhuǎn)化思想而言，所有的數(shù)學(xué)問(wèn)題都可以用已經(jīng)學(xué)過(guò)的知識(shí)解決，但究竟如何聯(lián)系卻是教學(xué)過(guò)程中的難點(diǎn)。教師在教學(xué)過(guò)程中經(jīng)常教的是“怎么做”，因此學(xué)生在實(shí)際解題過(guò)程中往往存在思維定勢(shì).為了突破這一困局，教學(xué)應(yīng)當(dāng)以“怎么想到這么做”為切入點(diǎn)，建構(gòu)起“條件—知識(shí)源”之間的關(guān)聯(lián)，并以此為抓手加強(qiáng)學(xué)法指導(dǎo)，切實(shí)提升學(xué)生分析問(wèn)題和解決問(wèn)題的轉(zhuǎn)化能力[1]。

知識(shí)溯源分析法關(guān)鍵有三步：明確解題目標(biāo)；追溯知識(shí)源；選擇知識(shí)源。知識(shí)溯源分析法的優(yōu)勢(shì)性在于：通過(guò)目標(biāo)鎖定明確解決問(wèn)題的思考方向，借助知識(shí)溯源掌握處理問(wèn)題的轉(zhuǎn)化策略，依據(jù)過(guò)程分析提升受阻思維的調(diào)控技巧，從而不僅詳細(xì)地剖析輔助線生成的來(lái)龍去脈，在呈現(xiàn)“怎么做”的同時(shí)更加明晰“為什么這么做”，強(qiáng)化對(duì)學(xué)生轉(zhuǎn)化能力和遷移能力的有效培養(yǎng)[2]。

二、基于圖形載體的中點(diǎn)溯源

借助知識(shí)溯源分析法，可以在初中數(shù)學(xué)中，對(duì)中點(diǎn)有關(guān)的知識(shí)點(diǎn)在整體視角下基于圖形的載體進(jìn)行精準(zhǔn)溯源。首先在初中里面和中點(diǎn)直接有關(guān)的第一個(gè)概念便是中線。在初中的學(xué)習(xí)過(guò)程中，可以把三角形的種類作為分類依據(jù)，對(duì)中線作用進(jìn)行梳理。在任意三角形中的中線作用為平分線段，平分面積。而在等腰三角形中，中線的另一作用便是三線合一，即底邊上的中線、高線和頂角的角平分線重合。在直角三角形中，斜邊上的中線又衍生出來(lái)斜中線定理[3]。

另外一個(gè)中點(diǎn)衍生知識(shí)點(diǎn)便是中位線。與中線不同的是，連接同一個(gè)三角形兩邊上中點(diǎn)時(shí)，便產(chǎn)生了中位線。當(dāng)然，中位線的難點(diǎn)不僅僅是找到中位線，而更重要的是能在解題過(guò)程中理解中位線平行于第三邊且等于第三邊的一半，因此這里要建立二級(jí)鏈接，即中點(diǎn)-中位線-三角形第三邊。

其次，如果中點(diǎn)和垂線相聯(lián)系，便會(huì)產(chǎn)生中垂線，中垂線的性質(zhì)非常豐富，其最重要的性質(zhì)為中垂線上的點(diǎn)到線段兩端距離相等。而同一個(gè)三角形中三邊上的中垂線相交，便構(gòu)成了三角形的外心，三角形的外心又是圓中的一個(gè)重要概念。

最后，將中點(diǎn)放在圓中來(lái)看，除了弦的中點(diǎn)還可以是弧的中點(diǎn)，而不論是哪種，都可以與垂徑定理建立聯(lián)系，而將弧的中點(diǎn)和弦的中點(diǎn)作為能相互推導(dǎo)的結(jié)論，便可以聯(lián)想到圓心角定理及其推論，而弧與圓周角度數(shù)是一一對(duì)應(yīng)的，因此也可以聯(lián)想到圓周角定理。

三、借知識(shí)溯源探本質(zhì)

實(shí)際上能夠根據(jù)條件聯(lián)想到所需要的知識(shí)源固然重要，但只根據(jù)知識(shí)源也不能做到一題多解，解法多樣，最重要的不僅僅是關(guān)注多解的挖掘，更重要的是關(guān)注對(duì)多解生成本源的思考。下面在知識(shí)溯源的基礎(chǔ)上，以具體題目為例探究一題多解生成的本質(zhì)。

1.基于選擇知識(shí)源不同產(chǎn)生多解

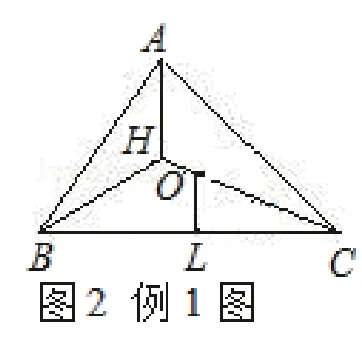
例1.如圖，已知H是△ABC的垂心，O是外心，OL⊥BC于L.求證：AH＝2OL。

分析：對(duì)于這道題目而言，條件較為簡(jiǎn)單。其中垂心的作用，便是延長(zhǎng)構(gòu)造出諸多的垂線。而三角形的外心很自然地可以聯(lián)想到構(gòu)造△ABC的外接圓，因此可以得到第一種方法。

另外基于外心，可以逆向追溯，從外心的本質(zhì)入手，中垂線與垂心相互聯(lián)系，可以得到多對(duì)平行，再結(jié)合中位線的性質(zhì)，可以構(gòu)造出來(lái)平行四邊形，因此得到第二種方法。

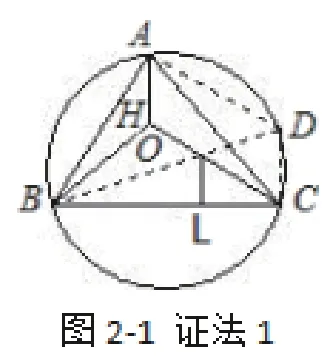
證法1：如圖2-1，作△ABC的外接圓⊙O，連接BO并延長(zhǎng)交⊙O于D，連接CD，AD，由中位線易得CD=2OL.又因CD⊥BC，AH⊥BC，可得AH∥CD.同理，AD∥HC，得四邊形AHCD為平行四邊形，可得AH=CD，即AH=2OL。

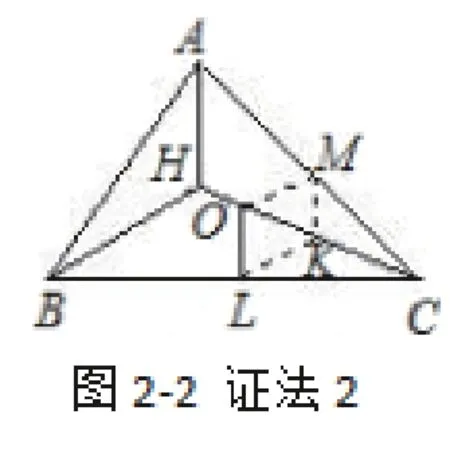
證法2：如圖2-2，作OM⊥AC于M，取CH的中點(diǎn)K，連接MK，LK，則有MK∥AH∥OL，LK∥BH∥OM，可得四邊形OLKM為平行四邊形，則MK=OL.又MK＝AH，所以AH=2OL。

證法比較：兩種方法基于不同的處理路徑，一種是基于外心的合情推理，一種從外心的本質(zhì)出發(fā)，再由中點(diǎn)進(jìn)一步聯(lián)想，通過(guò)中位線進(jìn)行聯(lián)系，兩種方法殊途同歸，不分伯仲，也切實(shí)證明了選擇知識(shí)源不同多解可行性。

2.基于構(gòu)圖位置不同產(chǎn)生多解

例2：在△ABC中，P為邊AB上一點(diǎn).M為CP的中點(diǎn)，AC＝2，AB＝3，∠PBM＝∠ACP，求BP的長(zhǎng)。

分析：基于題目中所給的∠PBM＝∠ACP，可以延長(zhǎng)BM與AC相交，這樣便可以得到兩對(duì)相似，進(jìn)而由兩對(duì)相似的對(duì)應(yīng)線段比構(gòu)造等量關(guān)系可以求出BP的長(zhǎng)。

從另一個(gè)角度來(lái)看，當(dāng)一個(gè)中點(diǎn)無(wú)法形成有效聯(lián)想，那么從題中觀察到，如果取AP的中點(diǎn)可以構(gòu)造出中位線，而這條中位線既可以聯(lián)系A(chǔ)C，又可以將轉(zhuǎn)換到∠PBM和∠ACP斜A型相似的基礎(chǔ)模型中，從而構(gòu)造方程求解。其次，如果把BM當(dāng)作中位線考慮，可以通過(guò)倍長(zhǎng)BP的方式構(gòu)造出相似三角形，同樣也可以求解。

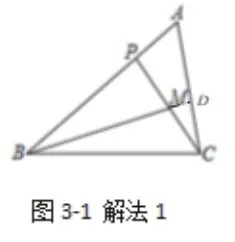
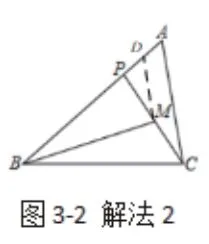
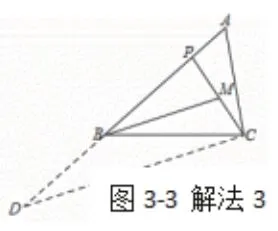
解 法3：如 圖3-3，延 長(zhǎng)PB至 點(diǎn)D，使BP=BD，連接CD.設(shè)BP=x，則PD=2x，∠PBM=∠ACP=∠PDC，∠PAC=∠CAD，可得△APC～△ACD.由AC2=AP·AQ得22=（3-x）（3+x），可得BP=x=

解法比較：對(duì)于上述三種解法，可以看到，如果單單把中點(diǎn)當(dāng)作中線來(lái)考慮，雖然也可以解決該問(wèn)題，但是不管從計(jì)算量還是思維難度上來(lái)講都要求較高。但如果將中點(diǎn)放在中位線的角度來(lái)看，通過(guò)合理地添加輔助線，可以有效減少計(jì)算量，減少思維的難度，并且將圖像轉(zhuǎn)換到我們熟知的A字形和斜A型相似，利用射影定理能快速求解。

3.基于輔助線的表述不同產(chǎn)生多解

同一輔助線從不同的角度描述，往往會(huì)產(chǎn)生不同的解題思路。以例題2解法3為例，較為簡(jiǎn)單的，若輔助線的表述為“延長(zhǎng)PB至點(diǎn)D，使PD=2BP”，那么需要從PD=2BP推得BM為中位線。若輔助線的表述為“作CD//BM，交AB延長(zhǎng)線于D”，需要通過(guò)CD//BM推得△BPM～△DPC，進(jìn)而得到BP=BD。再進(jìn)一步，輔助線的表述還可為“作∠BCD=∠CBM，交AB延長(zhǎng)線于D”，此時(shí)需要從∠BCD=∠CBM得到BM//CD。

解法雖然并不會(huì)因?yàn)檩o助線的作法不同而產(chǎn)生思路上本質(zhì)的改變，但是不同輔助線的表述及后續(xù)的推導(dǎo)過(guò)程也體現(xiàn)了數(shù)學(xué)的嚴(yán)謹(jǐn)性與邏輯性，而這恰恰也是學(xué)生經(jīng)常忽略并所欠缺的點(diǎn)。

4.基于不同知識(shí)體系的關(guān)聯(lián)性產(chǎn)生多解

例3：如圖，AB是⊙O的直徑，且AB＝10，弦CD⊥AB于點(diǎn)E，G是弧AC上任意一點(diǎn)，延長(zhǎng)AG，與DC的延長(zhǎng)線交于點(diǎn)F，連接AC，BC，DG.若求DG的長(zhǎng)。

分析：題目中的弦CD⊥AB，AG=BG很自然聯(lián)想到垂徑定理，由垂徑定理可以得到AB⊥OG，那么很自然地聯(lián)想到求DG的長(zhǎng)度便是構(gòu)造直角三角形，利用AB＝10很容易得到所需的直角三角形的各邊長(zhǎng)，從而求解。從不同知識(shí)體系上講，建立平面直角坐標(biāo)系求點(diǎn)D、G的坐標(biāo)，從而通過(guò)兩點(diǎn)間距離公式求出DG的長(zhǎng)度。

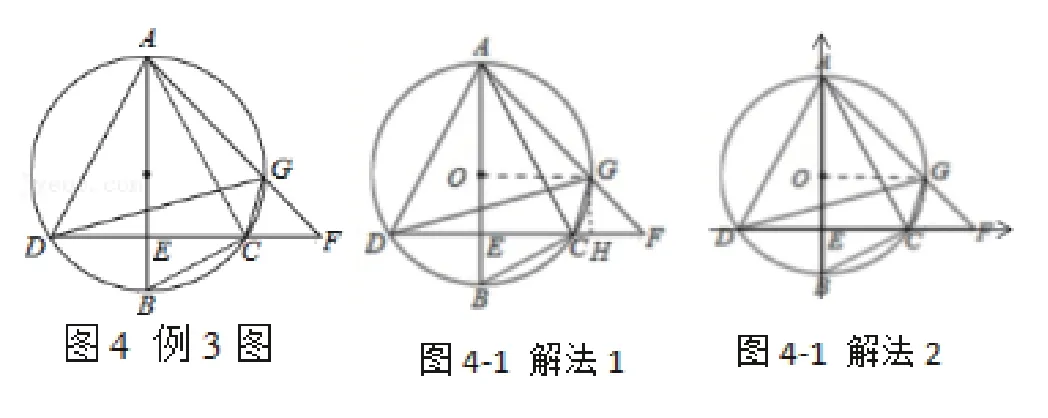
解法比較：兩種解法雖然在解題過(guò)程中有所相似，但垂徑定理在兩個(gè)種解法中起到的作用卻有所差異。但兩種解法起始的知識(shí)體系有著本質(zhì)的不同，第一種解法是立足于幾何的圖形直觀，通過(guò)尋找線段的等量關(guān)系，再結(jié)合求不共線線段的長(zhǎng)度一般性做法求解。另一種是基于解析幾何的一般觀念，通過(guò)求點(diǎn)的坐標(biāo)，再結(jié)合已經(jīng)有的公式進(jìn)行求解。這種多解的思考過(guò)程，無(wú)疑拓寬了思維的廣度。

四、教學(xué)導(dǎo)向

1.構(gòu)建知識(shí)網(wǎng)絡(luò)，提高知識(shí)完備性

初中階段學(xué)生對(duì)需要作輔助線的題目感覺(jué)到困難的原因，很大一部分是教師很多時(shí)候只教怎么做，不教怎么想，教師只分析解題過(guò)程，學(xué)生的“懂”，也僅僅停留在解題過(guò)程中的聽(tīng)懂層面，并未了解解題思路生成的本質(zhì)。因此教師在教學(xué)過(guò)程中更加應(yīng)當(dāng)關(guān)注基于條件的知識(shí)溯源挖掘，幫助學(xué)生構(gòu)建更加嚴(yán)密完整的知識(shí)網(wǎng)絡(luò)，并能夠打通各塊知識(shí)之間的聯(lián)系，而這又離不開(kāi)教師本身對(duì)于教材知識(shí)的發(fā)掘與整理，只有教師做到知識(shí)體系的充分完整，才能夠讓學(xué)生體會(huì)到各部分知識(shí)之間的聯(lián)系。當(dāng)學(xué)生的知識(shí)網(wǎng)絡(luò)逐漸完善，那么輔助線的作法自然不在話下，一題多解便能有其生長(zhǎng)的基礎(chǔ)條件。

2.掌握基本構(gòu)圖，提高轉(zhuǎn)化能力

然而事實(shí)上很多時(shí)候就算有完備的知識(shí)儲(chǔ)備，解題過(guò)程也并非一帆風(fēng)順，遇到困難也在所難免。這就要求教師在日常教學(xué)過(guò)程中更應(yīng)該對(duì)一些重要的轉(zhuǎn)化技巧進(jìn)行提煉、總結(jié)、升華。首先學(xué)生應(yīng)掌握基本圖形的構(gòu)圖策略，這是提升學(xué)生轉(zhuǎn)換技巧的重要途徑，例如倍長(zhǎng)中線和構(gòu)造中位線是處理線段中點(diǎn)的兩大基本技巧，構(gòu)造A字形、八字形相似也是建立邊與邊之間聯(lián)系的重要橋梁。其次，重現(xiàn)圖形的演變過(guò)程更有利于理解，例如先將復(fù)雜圖形的基本結(jié)構(gòu)抽離出來(lái)，讓學(xué)生進(jìn)行辨識(shí)，緊接著逐步添加線段或圖形演變?yōu)樽罱K圖像，讓學(xué)生一步步分析，明確添加的線段的作用以及將會(huì)產(chǎn)生的關(guān)聯(lián)，幫助學(xué)生系統(tǒng)性地學(xué)習(xí)分析問(wèn)題的方法，這樣一題多解才有生長(zhǎng)點(diǎn)。