一種基于Lorenz-Duffing混沌系統的視頻圖像加密新算法

涂 立，汪 彥

(1. 電子科技大學中山學院 機電工程學院，廣東 中山 528402；2. 湖南城市學院 信息與電子工程學院，湖南 益陽 413000)

隨著網絡和多媒體通信的高速發展，視頻技術在生活中得到了廣泛應用.由于網絡具備開放性的特點，圖像視頻信息的安全性受到了公眾的廣泛關注與重視，其相關研究顯得非常重要.在視頻圖像安全研究領域，加密是最為有效的方法，但是視頻的數據量比常規的靜態圖像要大，而且要求有一定的實時性，因此，對視頻的加密技術提出了更高的要求.

混沌系統具有良好的偽隨機性和對初值的高度敏感性，因此其被作為一種創新型研究應用于加密系統中.1989 年，著名數學家Robert A J Matthews 首次將混沌理論應用于保密通信，并提出了一種基于改進的Logistics 映射的數據加密方法.此后，大批學者在混沌加密研究方面取得了豐碩的研究成果.如Chen 等[1]提出先利用三維貓映射置亂加密，再利用混沌序列進行混合加密的算法；張錯玲等[2]提出了基于Lorenz 超混沌理論的圖像加密算法；朱艷平[3]提出了基于CNN 超混沌的視頻加密新算法；Elamir 等[4]提出了由混沌映射和DNA 計算編碼規則組合而成的密鑰加密新算法；牛瑩等[5]改進了約瑟夫遍歷問題，將其與DNA 編碼技術相結合并應用到圖像加密中.以上加密算法均屬于低維混沌映射，動力方程簡單，密鑰的敏感性不夠高，所設計的密鑰系統的密鑰空間較小，使得加密算法不夠安全.為了在安全性和穩定性等方面均達到較好的效果，還需要進一步研究新的視頻加密算法.

因此，本文基于Lorenz 和Duffing 復合超混沌系統，提出了一種新的視頻圖像加密算法，并對其加密效果等相關性能進行了仿真測試.

1 混沌系統理論

1.1 Lorenz 混沌系統

1963 年，美國氣象學家Lorenz 提出了混沌理論(Chaos)，指出在三階非線性自治系統中會出現非周期的無規律行為[6-9].Lorenz 系統方程式可表示為

將步長固定為0.01，并分別取a=10、b=28、c=8/3(組合參數1)和a=20、b=30、c=5/3(組合參數2)，經過迭代計算，可以得到圖1 所示的Lorenz系統吸引子圖.由圖1 可知，選取一定的參數組合，Lorenz 系統可表現為混沌狀態.

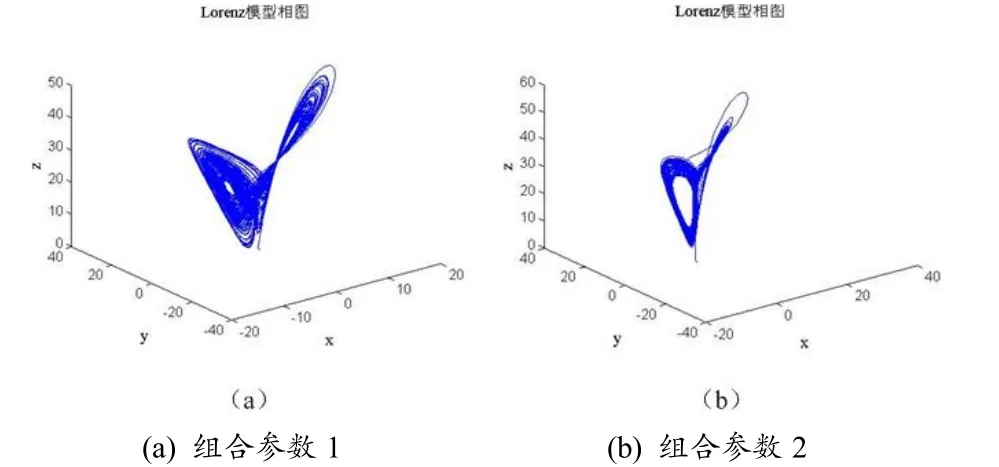
圖1 Lorenz 系統吸引子圖

1.2 Duffing 混沌系統

Duffing 混沌系統方程式可表示為

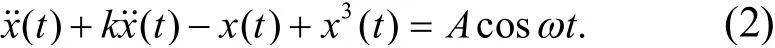
其中，k為Duffing 系統的阻尼系數[10-12]；x(t)+x3(t)為系統恢復力；Acosωt為外加周期激勵.

當參數ω取值為1 時，Duffing 系統方程可以簡化為

當選取參數k=0.1、a=48 時，該系統處于混沌狀態，其X-Y平面的相圖以及變量x的時域響應如圖2 所示.

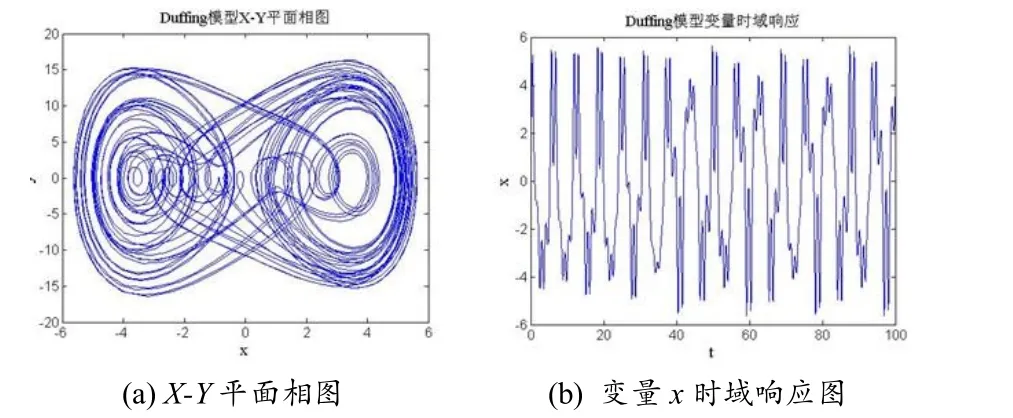
圖2 Duffing 系統相圖和變量x 時域響應圖

1.3 Lorenz-Duffing 復合混沌系統

將Duffing 混沌系統的方程轉換成等價方程，并且引入Duffing 方程的外部激勵w˙=gx，使得Duffing 系統成為自治系統；同時在Lorenz 系統中的第1 項加入dzu-w作為反饋控制器，以此連接2 個混沌系統，構建一個六維Lorenz-Duffing復合混沌系統，其動力學方程式為

取圖3 所用參數進一步分析，得到該系統時域響應如圖4 所示.

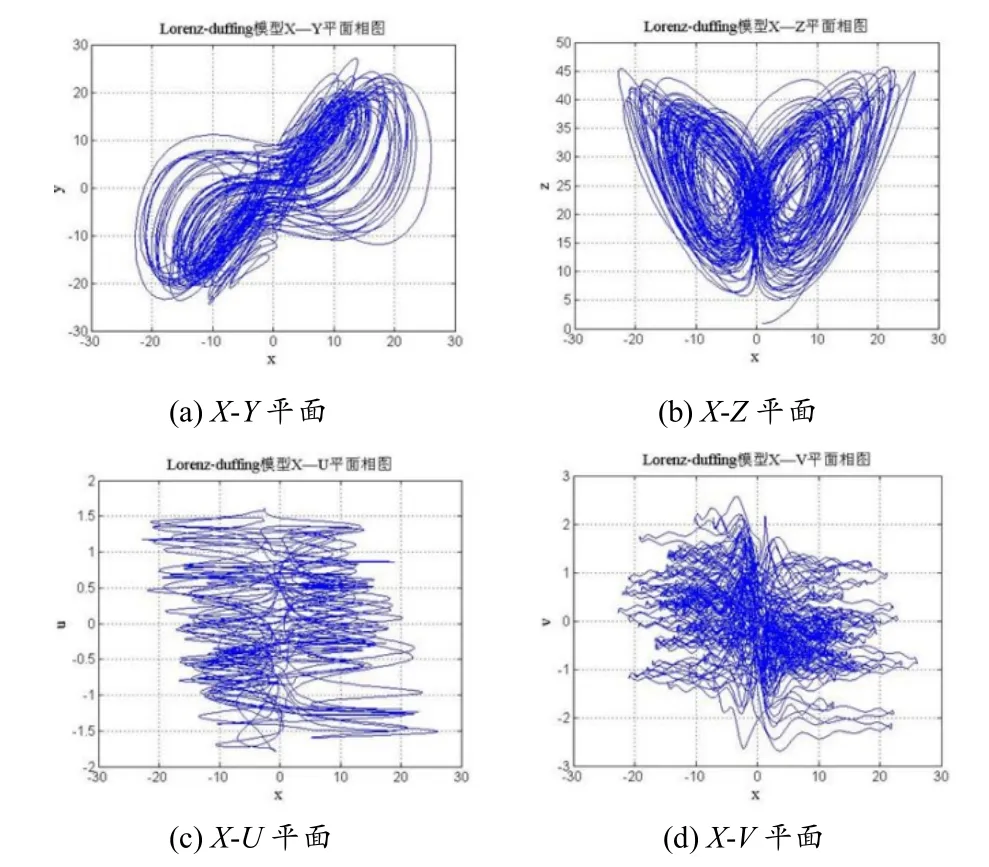
圖3 六維混沌系統相圖

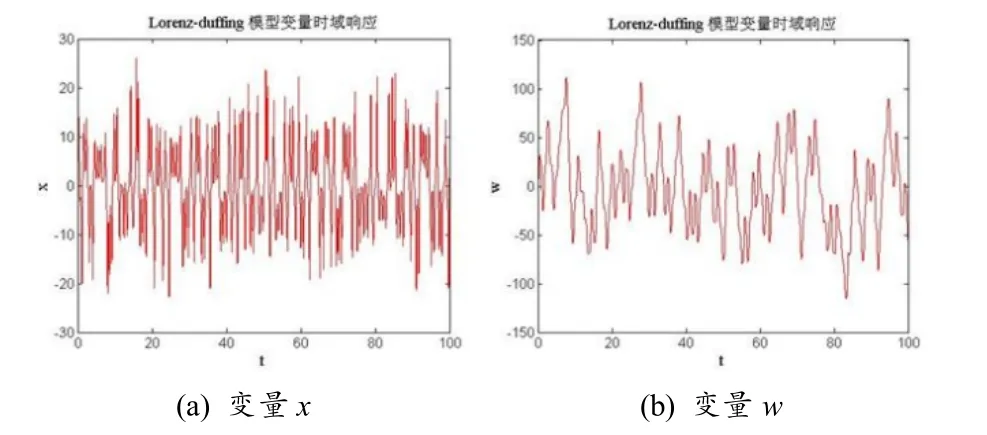
圖4 六維混沌系統時域響應圖

由圖3～圖4 可知，新構建的Lorenz-Duffing六維混沌系統有良好的混沌特性，可以應用于視頻和圖像的加密.

2 算法步驟

視頻圖像加密算法的步驟如下：

1)用高清攝像頭實時采集視頻，采用H.264視頻編碼標準對原始視頻進行壓縮并轉存為video 文件.

2)導入壓縮視頻，利用VideoReader 工具包讀取視頻信息(在4-Duint8 格式文件Frame 中).

3)將Frame 文件轉換成mov(k).cdata，其中k為視頻幀數，所得RGB 數據全部轉換成bmp 格式的圖片.

4)劃分k個數據存儲單元，讀取視頻轉換后圖片中的第i幅圖片，將該圖片的像素矩陣分解成紅(R(m,n))、綠(G(m,n))、藍(B(m,n)) 3 個分量，存儲在對應的第i個數據存儲單元中.

5)利用Lorenz-Duffing 方程生成3 個一維混沌序列U、V、W，這3 個混沌序列的長度均為待加密圖像的像素數量m*n.

6)對3 個混沌序列進行優化.先取出序列值小數點后的第2、4、6 位小數，把這3 個數組成1 個3 位十進制數，再把該十進制數對256 求余數，生成優化后的U1、V1、W1混沌序列.

7)對圖像進行約瑟夫環位置加密.先在2～20取E和F2 個整數(F＜E)；再讀取視頻轉換后圖片中的第i幅圖片，并把該圖片的紅色分量部分(R(m,n))轉換成一維數組K（m*n）.

8)對紅色分量圖像R(m,n)進行加密.即把數組K（m*n）中的m*n個元素依次排列成環，從K(1)開始報數至K(E)，把第F個數即K(F)取出來，放入J數組中；從K(E+1)開始，繼續從1 開始報數至E，取出第2 輪報數的第F個數，再放入數組J中；如此循環報數取值，直到K數組中的數值全部放入數組J中為止，得加密數組J（m*n）.

9)將步驟6)中所得U1、V1、W1轉換成m*n形式，即U1（m*n） 、V1（m*n） 、W1（m*n），并與J（m*n）依次進行異或運算，所得結果Ri(m,n)即為加密后的紅色分量圖像.

10)對第i幅圖片的綠色分量和藍色分量部分均采用相同方法進行加密，可得加密后的Gi(m,n)和Bi(m,n).

11)將Ri(m,n)、Gi(m,n)和Bi(m,n)矩陣還原成加密視頻的像素矩陣F，即為第i幀加密后的視頻圖像.

12)循環執行上述加密步驟，完成所有原始圖片加密工作，并把所有加密幀進行重新整合，得到最終的密文視頻流.

解密過程是加密過程的逆運算，收、發均采用相同的混沌序列參數，原始視頻信號才能從加密視頻信號中解調出來.需要注意的是，整個解密過程需要先進行像素值的灰度解密，再進行約瑟夫環位置解密，否則無法得到正確的解密視頻.

3 仿真測試與結果分析

3.1 實驗環境和視頻圖像加密

實驗環境：硬件系統為 Intel Core(TM)i5-7400 CPU E5300@3.0 GHz，8.00 GB 內存的計算機；軟件系統包括Microsoft Windows 10 專業版操作系統和Matlab 7.10.0.499 (R2010a)版本仿真軟件.

實驗以所得第20 幀圖像作為原始圖像對視頻進行轉換，如圖5(a)所示.經紅色分量轉換后的灰度圖像如圖5(b)所示(以下實驗均以圖5(b)作為仿真圖像).

圖5 第20 幀采樣圖像

選取參數a=10、b=8/3、c=28、d=-2.5、e=0.6、f=-8 和g=9.7，變量x、y、z、u、v、w初值均為1，時間步長為 0.01，進行迭代計算，得到U1、V1、W1 3 個長度為65 536 的一維序列；將約瑟夫環位置加密參數設置為E=7 和F=4，對第20 幀原始彩色圖像(圖5(a))經紅色分量轉換后的灰度圖像(圖5(b))進行加密，得到其約瑟夫環加密圖如圖6(a)所示；進一步對該加密圖進行像素值加密，得到的最終加密效果圖如圖6(b)所示.

圖6 圖像加密

3.2 直方圖分析

直方圖(histogram)又被稱為柱狀圖，是一種統計報告圖.圖像的直方圖被用來統計圖像像素點出現的數量，其中橫坐標表示圖像的像素值；縱坐標表示該像素值出現的次數.直方圖能夠很直觀地反映出圖像加密的效果，即對于加密圖像，若其加密安全性能高，那么它各像素點出現的次數是比較均勻的.圖像加密前后的直方圖如圖7 所示.

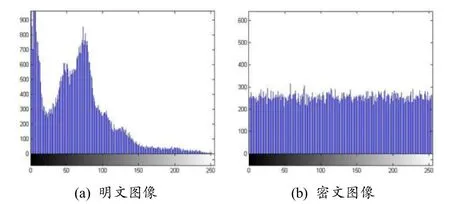
圖7 直方圖分析

由圖7(a)可知，加密前各像素級的像素分布波動非常大，其中一些像素值出現的頻率很大，而另一些像素值出現的頻率就非常小.圖7(b)是圖像加密后的直方圖(密文圖像).由圖7(b)可知，加密后各像素級的像素分布非常均勻，因此掩蓋了原始圖像各像素級像素的分布規律，能夠很好地抵御統計分析學的進攻.

3.3 相鄰像素點的相關性分析

圖片像素相關性[13]被用來表示圖像中2 個像素點間的關系，它可以準確地反映加密算法的加密效果.相關性系數可用協方差表示，其計算公式為

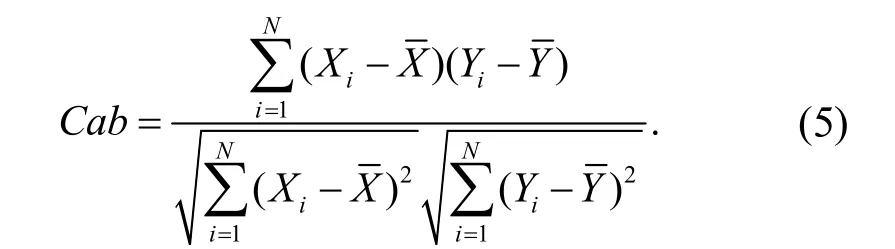
相關性系數Cab范圍為0～1，其值越接近1，說明圖像相關性越強，加密效果越差；其值越接近0，說明圖像相關性越弱，加密效果越好.

從明文圖像和密文圖像中各取5 000 個位置相同的像素點，分別計算出這些相鄰像素點在水平、垂直和對角線方向的相關系數，結果如表1所示.

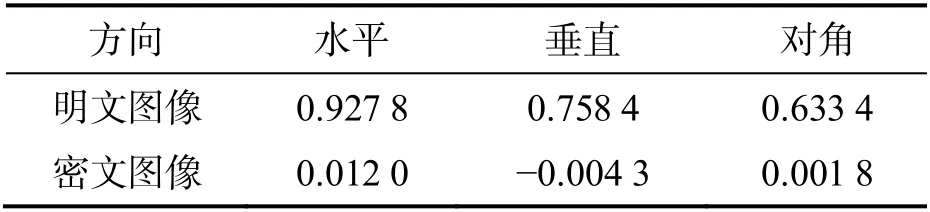
表1 相鄰像素的相關系數

由表1 可知，明文圖像中相鄰像素的相關系數比較大，表明相鄰的像素具有高度相關性；密文圖像中相鄰像素的相關性系數均值為0.003 17，接近0，表明相鄰的像素已基本不相關.這說明所提算法的加密效果具有非常好的擴散性和加密性，對統計分析攻擊具有良好的抵御性.

通常，還可以采用圖像3 個方向(水平、垂直和對角線)上相鄰像素點的相關性分析來了解其加密效果.從明文圖像和密文圖像中各選取5 000 個像素點，分析其水平、垂直和對角線相鄰的相關性，結果分別如圖8～圖10 所示.

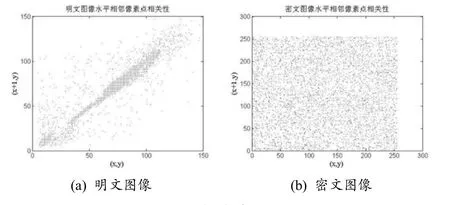
圖8 水平相鄰像素相關性分析

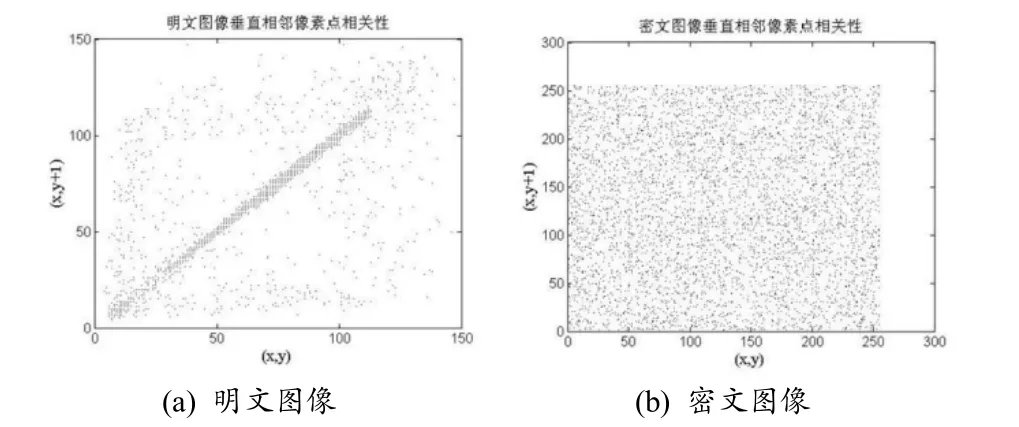
圖9 垂直相鄰像素相關性分析

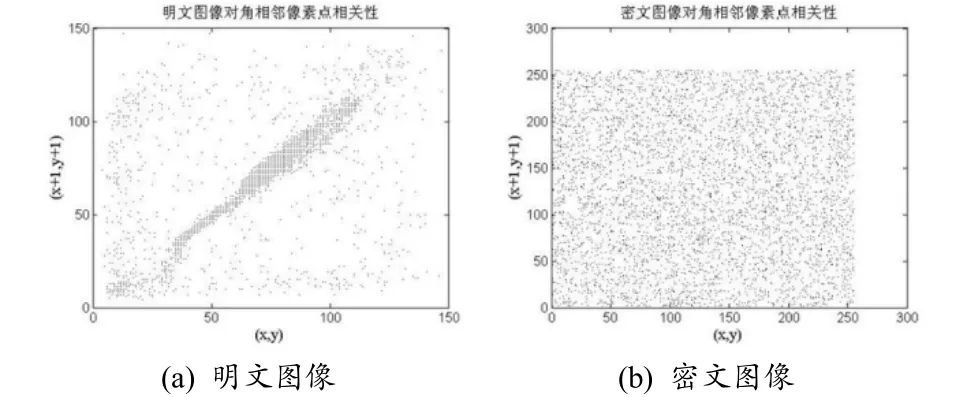
圖10 對角相鄰像素相關性分析

由圖(8)～圖(10)可以看出，明文圖像選取出來的點與相鄰點的數值是非常接近的，而密文圖像選取出來的點與相鄰點沒有明確的線性相關，呈混沌分布狀態.

3.4 MSE 和PSNR 分析

MSE(mean squared error)為均方誤差，是衡量“平均誤差”的一種較方便的方法.其值越小，說明原始圖像與加密圖像間的聯系越小.其計算表達式為

PSNR(peak signal to noise ratio)表示峰值信噪比，其單位為dB.PSNR越大，表示圖像失真程度越少；反之，圖像的失真程度越大.但對加密圖像來說，PSNR越小，加密效果越好.其計算表達式為

3.5 密鑰敏感性分析

由圖11 可知，即使密鑰參數發生極微小的變化，也不能成功解密，這說明本加密算法的密鑰具有很高的敏感性.

圖11 不同密鑰參數的解密效果

當密鑰參數細微變化時，經重新計算，得出解密圖像的MSE和PSNR，結果如表2 所示.

表2 密鑰敏感性分析

由表2 可知，所有情形下解密圖像的MSE均非常大，PSNR均很小.這說明解密圖像的失真程度很大，所提加密算法的密鑰敏感性很高，具有較高安全性.

3.6 信息熵分析

信息熵是指某種指定信息出現的概率，它可以體現出一個系統的有序化程度.信息熵的值越小，表示系統有序性越好；信息熵的值越大，表示系統越混亂.在圖像加密中，信息熵可被用來表示圖像中灰度值的分布情況及其出現概率，即其值越大，表示圖像中灰度分布越均勻，加密算法的保密性就越強；反之，加密效果就越差.

信息熵[14]計算公式為

3.7 密鑰空間分析

密鑰空間是一項用來衡量加密算法抵御暴力攻擊的重要指標.如果要抵御暴力破解，加密算法的密鑰空間的長度至少要達到100 位[15].本加密方法中使用的加密參數x、y、z、u、v、w均可作為密鑰，假設密鑰敏感性為10-10，且僅考慮參數u、v、w(其中u=[-1.7，1.7]、v=[-2.6，2.6]、w=[-115，115])，則u、v、w的取值分別有3.4×1010、5.2×1010和2.3×1012種可能.整個算法的密鑰空間為4.066×1032，密鑰空間長度為108 位，若用1臺2.6 GHz 主機進行破解，所需時間為4.33×1015a，窮舉搜索破解幾乎不可能實現.

4 結論

1)基于Lorenz 和Duffing 低維混沌系統，構建了高維復合混沌系統，該系統包含多個參數和自變量，具有更好的混沌特性和更大的混沌區間.

2)針對Lorenz-Duffing 高維復合混沌系統所提出的視頻圖像加密算法擴展了密鑰空間，使得暴力和已知明文攻擊等破解方法更難解密，其具有更高的安全性，也具有更好的加密效果.