依托數學文化 玩轉平面向量

湖北省襄陽市第四中學 (441021) 范 娜湖北省襄陽市第一中學 (441000) 王 勇

數學文化是貫穿整個高中數學的重要內容，在高考中，以數學文化為命題背景的試題立意深遠、構思精巧、內涵豐富，既能考查數學知識、能力、思想和方法，又能加深對中外數學文明的了解，增強愛國主義情懷，提高數學文化素養，豐厚數學文化底蘊.融入對數學文化的考查已成為新一輪高考命題改革的一個顯著特征.下面精選以數學文化為依托的平面向量問題七例并分類解析，旨在探索題型規律，揭示解題方法.

一、以“八卦模型圖”為依托

圖1 圖2

A.4 B.3 C.2 D.1

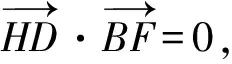
點評：本題中八卦模型圖只是為了引出八邊形ABCDEFGH的一個載體，重要的是理解平面圖形，即正八邊形ABCDEFGH所包含的幾何性質，在正八邊形ABCDEFGH中，通過對幾何圖形性質的理解，利用向量的和差運算、數量積運算等，逐一驗證給出的四個結論是否正確而得解.

二、以“趙爽弦圖”為依托

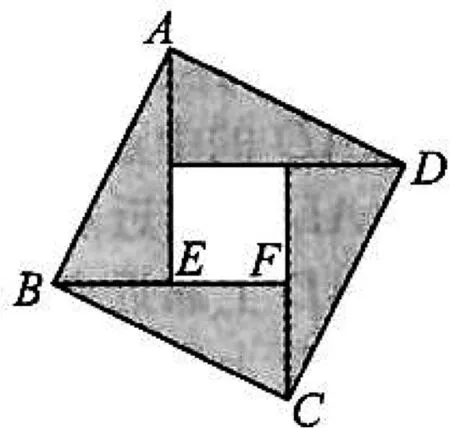
圖3

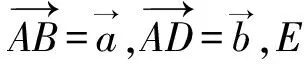
圖4

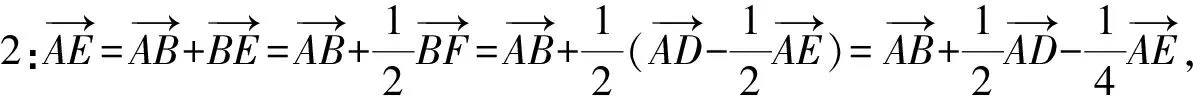
點評：本題借用“趙爽弦圖”考查平面向量的線性運算，具體推理時有一定的難度.

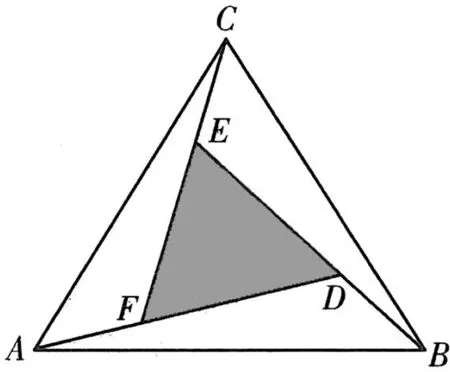
圖5

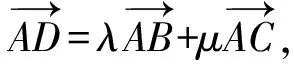
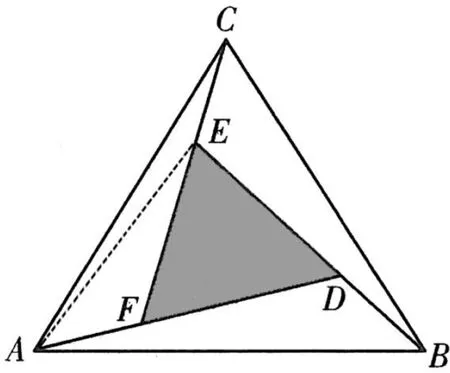
圖6

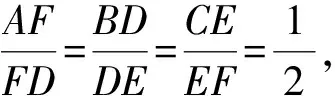
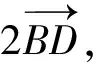
點評：本題以“趙爽弦圖”的類比圖為背景命制，新穎別致，韻味十足.主要考查平面向量的線性運算，具體推理時，需添加輔助線，極富思考性和挑戰性，是一道難得的好題.

三、以“黃金分割”為依托

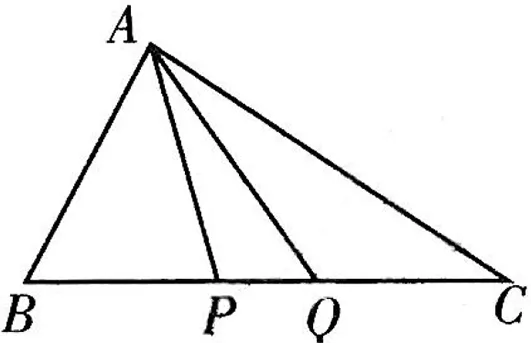
圖7

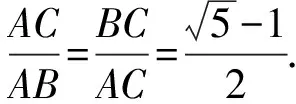
點評：本題以黃金分割數及黃金分割點為載體命制，主要考查平面向量的線性運算，對運算求解能力要求較高.

四、以“勾股定理”為依托

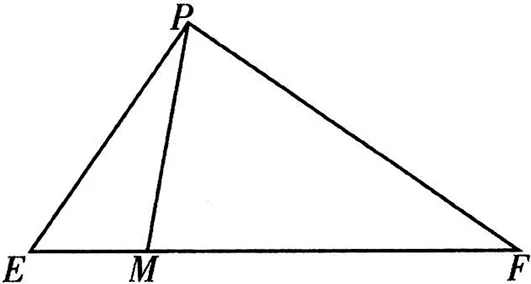
圖8

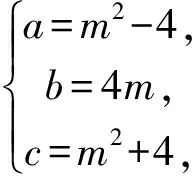
點評：本題首先通過已知確定三角形的三邊長，然后利用平面向量數量積運算求解即可.

五、以“歐拉線”為依托

例6 (2021·深圳市調考題)著名數學家歐拉提出了如下定理：三角形的外心、重心、垂心位于同一直線上，且重心到外心的距離是重心到垂心的距離的一半.此直線被稱為三角形的歐拉線，該定理則被稱為歐拉線定理.設點O,H分別是△ABC的外心、垂心，且M為BC的中點，則( ).

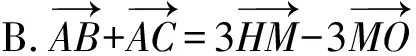
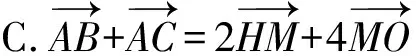
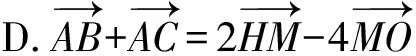
圖9

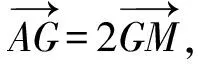
圖10

點評：本題以三角形的歐拉線及歐拉線定理為背景命制，主要考查平面向量的線性運算，具體推理時，有一定的難度.解法2利用特殊圖形法可輕松獲解，敬請同學們仔細品味和充分借鑒.

六、以“六芒星”為依托

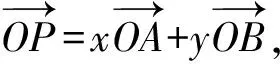
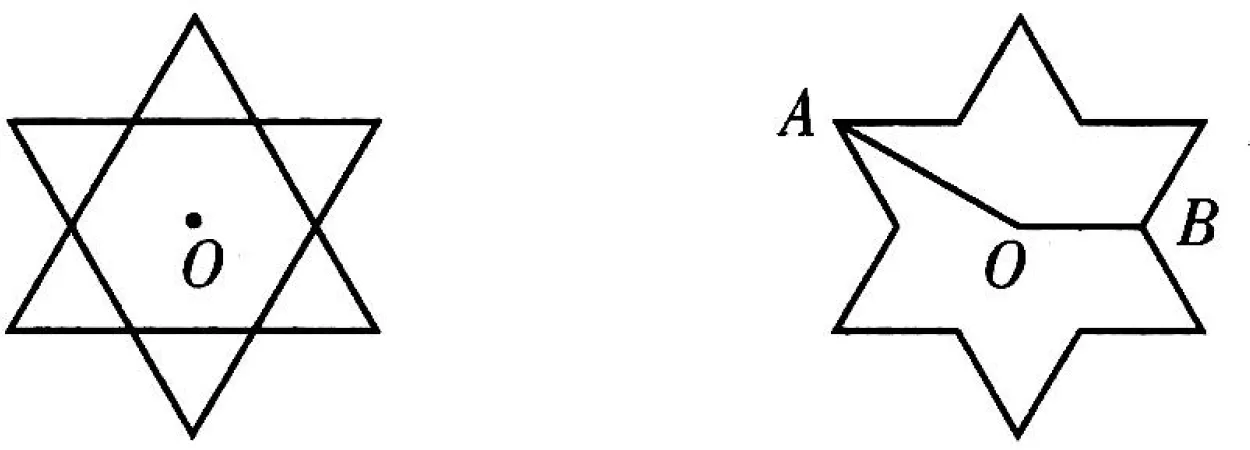
圖11 圖12

A．-6 B.1 C.5 D.9

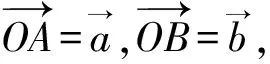
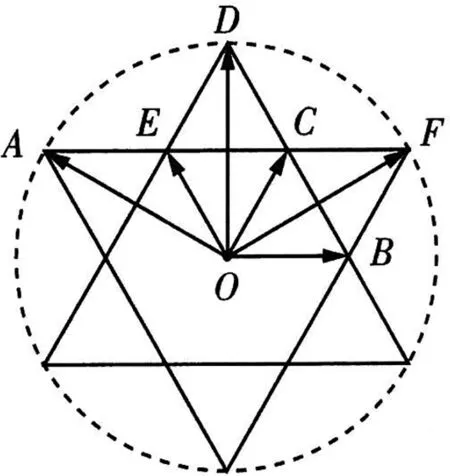
圖13

點評：本題是以“六芒星”為背景命制的多選題，圖形美觀大氣，主要考查平面向量的線性運算，分類討論思想考查充分，借助圖形的結構特征求出的取值范圍，進而求出的可能取值.

縱觀以上各例，我們發現，此類平面向量題一般是從中外優秀傳統文化中挖掘素材，將數學文化與平面向量知識有機結合，要求考生對試題所提供的數學文化信息材料進行整理和分析，在試題營造的數學文化氛圍中，考查平面向量的基礎知識、基本技能、基本思想、基本活動經驗，感受數學的思維方式，體驗數學的理性精神.