由一道菱形證明題引發(fā)的思考

湖南省長沙市長郡月亮島學校 (410200) 張月梅

菱形是一類特殊的平行四邊形，具有平行四邊形的共性和自身一些特殊性質(zhì)，是初中幾何教學的重點和難點，也是中考命題熱點，經(jīng)常與其他基本圖形結(jié)合進行考察. 本文通過一道菱形背景的幾何證明題，在梳理解題方法的同時，重在探究圖形內(nèi)部的聯(lián)系.

圖1

1.原題重現(xiàn)

如圖1，已知菱形ABCD中，∠BAD=120°，M為BC上一點，N為CD上一點.求證：若△AMN有一個內(nèi)角等于60°，則△AMN為等邊三角形.

2.思路分析

要證明△AMN為等邊三角形，已有一內(nèi)角為60°，只需證明△AMN中有兩邊相等即可.由于60°角位置不確定，需分∠MAN=60°、∠AMN=60°和∠ANM=60°三種情況討論，其中后兩種情況證明方法相同.

3.解法展示

如圖2，連接AC，易證△ABC和△ACD為等邊三角形，可得AC=AD，∠ACB=∠DAC=∠D=60°.

圖2

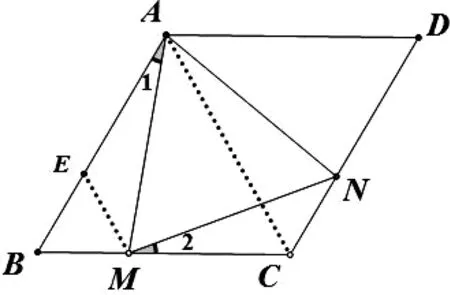
圖3

(1)若∠MAN=60°，則∠1+∠2=∠2+∠3=60°，所以∠1=∠3，可證△AMC≌△AND，得到AM=AN，進而完成證明.

(2)若∠AMN，如圖3，∠B+∠1=∠AMN+∠2，所以∠1=∠2.過點M作ME∥AC交AB于點E.易得△BEM為等邊三角形，所以BE=BM，∠BEM=60°，得到AE=MC，∠AEM=∠MCN，可證△AEM≌△MCN，得到AM=MN，進而完成證明.

圖4

若∠AMN=60°，還可以運用四點共圓方法創(chuàng)造條件進行證明.

如圖4，由∠ACD=∠AMN=60°，所以A、M、C、N四點共圓.所以∠ANM=∠ACB=60°，進而得到△AMN三個內(nèi)角均為60°，所以△AMN是等邊三角形.

(3)若∠ANM=60°，證明方法與(2)中相同，此略.

上面的解法中，(1)運用的是“角邊角”證明三角形全等的方法，(2)中方法一是“截長”構(gòu)造等邊三角形，得到三角形全等的條件，方法二則是利用四點共圓判定方法，先得到A、M、C、N四點共圓，再利用“同圓中相同的弧所對的圓周角相等”，得到∠ANM=∠ACB=60°，從而完成證明. 本題是多種幾何證明方法的綜合運用，很好地展現(xiàn)了菱形和等邊三角形這兩類初中幾何常見幾何圖形組合在一起，并蘊含豐富的數(shù)學思想.

4.解后探究

圖5

(1)原題給出含有一個60°內(nèi)角的菱形，同時要求“內(nèi)置”三角形有一個內(nèi)角為60°，最終得到了“內(nèi)置”三角形為等邊三角形的結(jié)論. 若將條件改為：如圖5，在菱形ABCD中，AC=AB，BM+DN=AB，可通過證明△ABM≌△ACN，證得“內(nèi)置”△AMN為等邊三角形.

(2)菱形ABCB′可看成由等腰三角形△ABC沿底邊AC翻折180°與原來三角形一起所成的圖形，也可看成由一個直角三角形Rt△ABO通過翻折(旋轉(zhuǎn))得到，如圖6所示. 所以菱形的性質(zhì)可由三角形中相關(guān)性質(zhì)推導得出.

圖6