控制棒下落與流體流動的耦合狀態方程及其保辛算法*

趙 珂，陳昌義，席炎炎，黃東威，吳 鋒，鐘萬勰

（1.大連理工大學 工程力學系 工業裝備結構分析國家重點實驗室，遼寧 大連 116024；2.中廣核研究院有限公司，廣東 深圳 518000）

（我刊編委鐘萬勰來稿）

引 言

控制棒是核反應堆在發生緊急情況時控制停堆的重要部件，控制棒的下落時間是保證核反應安全的關鍵指標.近年來，國內外許多學者對控制棒下落時間的問題做了大量研究：文獻[1]通過商業軟件ADINA 建立了單根控制棒二維流-固仿真模型，并將ADINA 得到的計算結果與未公開的企業內部代碼得到的結果進行比較，落棒時間誤差在7%以內；文獻[2]基于FLUENT 動網格算法，建立了單根控制棒三維流體仿真模型，將得到的控制棒落棒時間與試驗結果進行比較，誤差小于6%.采用二維、三維動力學模型的缺點是自由度多、計算量大，因此計算效率較低，往往只能分析單根控制棒，不能分析整個控制棒組件.考慮到控制棒和導向管均具有長細比大的特點，且控制棒的直徑與導向管的直徑相近，文獻[3]基于一維Navier-Stokes 方程建立了控制棒下落的數學模型，得到的結果能夠很好地匹配試驗結果；文獻[4-5]構建了基于一維Navier-Stokes 方程的落棒動力學模型，通過編譯C++程序進行計算.這些研究中常將流體與固體分開進行分析[4-5]：首先，假定控制棒的運動狀態恒定不變，計算流體流動的流量和壓強分布，得到流體阻力；然后，假定流體為擬穩態流動，其速度和壓強狀態不變，根據流體阻力計算控制棒的速度等變量.這種算法本質上是動力學求解算法中的算子分裂法[6]，因此只有一階精度，計算精度較低，需要取非常小的時間步長[3]才能保證“擬穩態流動”近似的精度.此外，控制棒下落過程中，流場中的流速、壓強等會發生非線性突變，采用單一的時間步長，算子分裂算法還存在不收斂問題，本文的研究將致力于解決這些問題.

在控制棒下落過程中，控制棒的下落與流體流動是同時發生的，因此應該采用流固耦合方法，以真實地描述控制棒的下落過程.基于流固耦合思想，本文首先建立了控制棒運動方程和導向管內流體壓降平衡的非線性微分方程組；然后引入關鍵恒等變換=v，得到非線性微分方程組的狀態方程.為精確求解該非線性狀態方程，本文建立了一種時間步長自適應保辛算法.該方法可以根據流動的實際狀態實時調整時間步長，精確捕捉流動狀態的突變，避免數值發散，并可以在流動變化平穩的時間段采用較大的時間步長，提高計算效率.

1 理論模型

1.1 物理模型

控制棒和導向管的縱剖面圖如圖1所示，其中陰影部分表示控制棒，控制棒下面是導向管，控制棒的直徑小于導向管的直徑，且控制棒的長度大于導向管的長度.導向管和控制棒全部豎直放置，導向管管壁和底部中心處均有流水孔，分別記為側孔和底部流水孔.導向管和控制棒完全浸在水中，底部流水孔保持進水狀態，而側孔存在流進和流出兩種狀態的突變.在控制棒下落過程中，導向管固定不動.初始時刻，控制棒在導向管側孔上方，如圖1(a)所示.控制棒由靜止釋放后，在重力、流體作用力等不同力的作用下開始下落，經過一段時間，控制棒底部下落至導向管側孔下方，如圖1(b)所示.

對圖1中的結構建立坐標.以導向管底部截面圓心為坐標原點o，以導向管中心軸為z軸，向上為正.圖1中，導向管底部Z0的坐標為0，對應的壓強為PZ0；導向管側孔的坐標為Z1，對應的壓強為PZ1；控制棒底部的坐標為Z，對應的壓強為PZ，Z在下落過程中會隨時間而變化；導向管頂部的坐標為Z2，對應的壓強為PZ2.

圖1(a)中，控制棒底部在導向管側孔上方.根據導向管內流量的不同可將導向管分成三個區間，分別為[Z,Z2]，[Z1,Z]，[Z0,Z1]，對應的流量分別記為Q2，Q1_Z，Q0.從導向管側孔流進或流出的流量記為Q1，以流出為正.同樣地，圖1(b)中也根據導向管內流量的不同，將導向管分成三個區間，分別為[Z1,Z2]，[Z,Z1]，[Z0,Z]，對應的流量記為Q2，Q1_Z，Q0，而導向管側孔處的流量仍記為Q1，以流出為正.

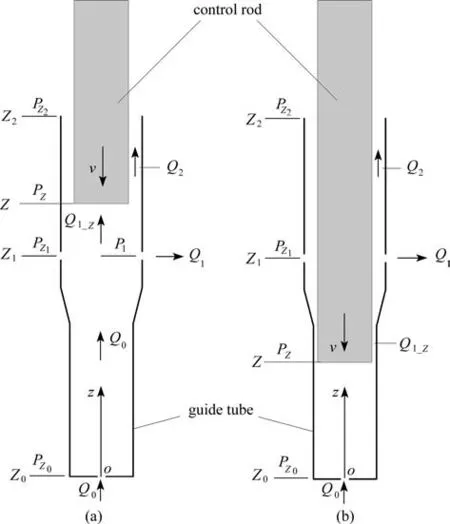
圖1 控制棒在導向管內的下落示意圖Fig.1 The falling diagram of the control rod in the guide tube

為方便論述，導向管頂部以上的控制棒部分所受的力暫不考慮；且假定控制棒在下落過程中保持豎直狀態，即控制棒沒有橫向偏移和橫向振動；反應堆內的流體滿足不可壓縮條件.

1.2 控制棒的運動方程

控制棒的運動受Newton 第二定律控制，其控制方程可以寫成

其中，M是控制棒的質量；w是控制棒的位移；表示控制棒的加速度；F是控制棒受到的合力，可表示為

式(2)中，Fg為控制棒的重力；Fb為控制棒受到的浮力；frod為控制棒受到的流體摩擦阻力；Fr為控制棒受到的流體壓差阻力；Fc為控制棒受到的機械摩擦力，由實驗擬合得到；Fs為控制棒受到的彈簧阻力，此力在控制棒快要到導向管底部時產生，防止由于控制棒速度過大從而與導向管產生強烈碰撞，可表示為

其中，Fprl表示彈簧預緊力，Ks表示彈簧剛度，hs表示控制棒接觸彈簧時的位移.

在某區間段[Za,Zb]內，摩擦力frod可表示為[7]

其中，ρ為流體密度，vf為流體流速，v為控制棒的下落速度，C2為控制棒的摩擦因數，l2為控制棒的濕周長，sgn為符號函數.

在式(2)所示控制棒受到的幾種合力中，重力和浮力很容易計算，摩擦阻力可通過式(4)來計算，而壓差阻力Fr的計算涉及到流體的非定常流動，計算相對復雜，將在下一小節詳細闡述.

1.3 壓降和壓差阻力計算

導向管內的流體流動可分為兩種情況，一種為圖1所示Q0對應的區間，流體在變截面的圓形導向管內流動；第二種為圖1所示Q2對應的區間，流體在變截面的導向管和控制棒之間的環形通道內流動.由于通道的長細比很大，流動可模擬為一維N-S 方程[1]：

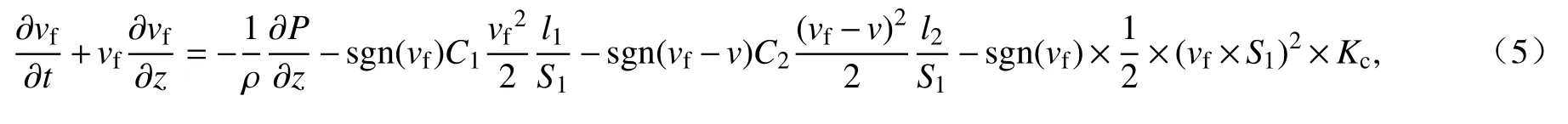
其中，t為時間，P為壓強，C1為導向管的摩擦因數，l1為導向管的濕周長，S1為控制棒與導向管之間的環形面積，Kc為局部形阻系數，由實驗測定，令環形面積之間的流量為Q=vfS1.將上式在區間 [Za,Zb]上積分，可得壓降方程：

引入如下變量：

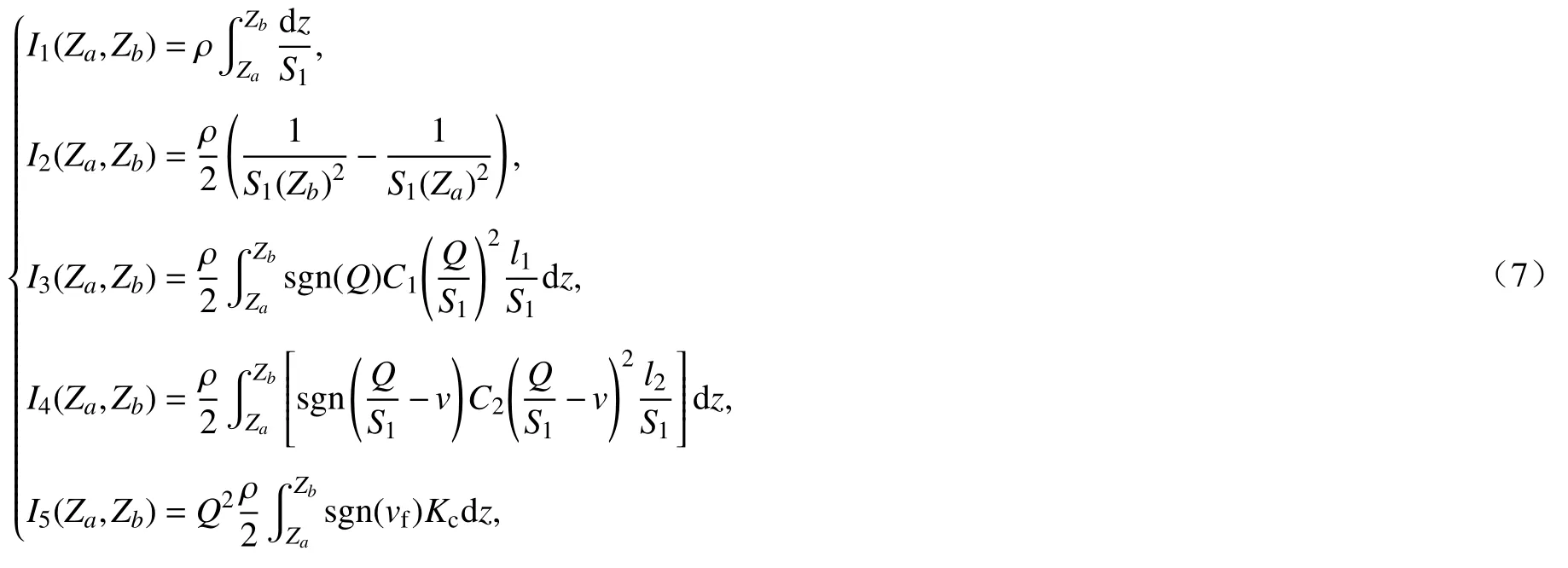
則壓降方程(6)化簡為

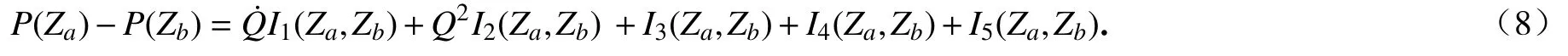
式(7)中的I1～I5均有特定的物理意義：I1表示由于局部加速度導致的壓降變化系數，稱為慣性壓降系數；I2表示對流加速度產生的壓降系數，稱為對流壓降系數；I3表示導向管受到的流體摩擦力產生的壓降；I4表示控制棒受到的流體摩擦力產生的壓降；I5表示由于導向管形狀改變產生的形阻壓降.根據求得的壓降，可進一步求出控制棒在區間[Za,Zb]受到的壓差阻力[5]：

其中，Srod表示控制棒的橫截面積.

以上分析討論的是導向管內存在控制棒時的壓降和壓差阻力計算.當導向管內沒有控制棒時，式(8)壓降的計算要減去控制棒摩擦力產生的壓降部分，即減去I4(Za,Zb)，則壓降方程為

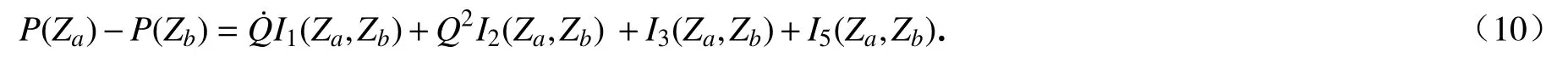
2 控制棒與流體耦合運動狀態方程

當控制棒底部在導向管側孔上部或者下部時，流場分布是不同的，壓降方程的建立以及控制棒所受壓差阻力的計算也是不同的，因此需分別討論.

2.1 控制棒底部在導向管側孔之上

首先討論控制棒底部在導向管側孔上部的情況.如1.1 小節論述，當控制棒底部在導向管側孔之上時，將導向管分成三個區間，分別為[Z,Z2]，[Z1,Z]，[Z0,Z1].在區間 [Z,Z2]內，由于流體在圓環內流動，其兩端壓降計算采用式(8)，可表示為

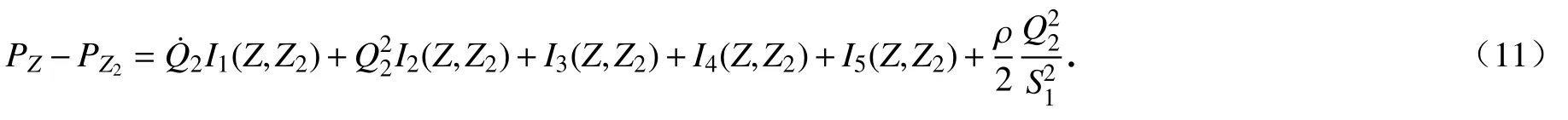
式(11)中的最后一項表示由于局部損失產生的壓降.為方便表示，記I11=I1(Z,Z2)，I11的第一個下標表示壓降類型，此處為慣性壓降系數；第二個下標表示導向管的區間，此處為區間[Z,Z2].其他壓降類型和其他導向管區間也類似表示，所以上式變為

在[Z1,Z]和 [Z0,Z1]兩段，流體在圓管內流動，因此可利用式(10)計算兩端壓強，分別表示為

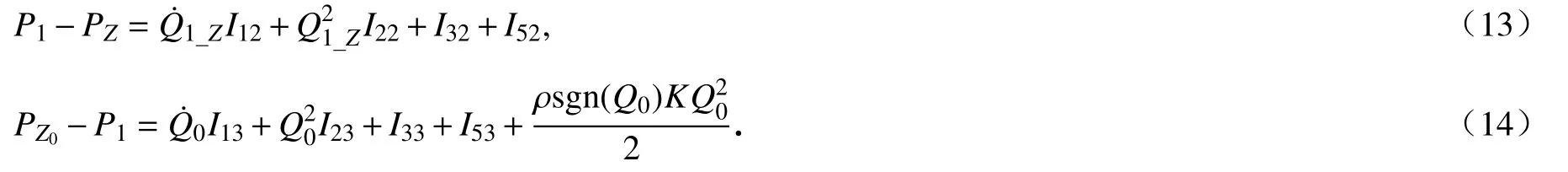
式(14)中最后一項表示流體從導向管底部流水孔流進導向管時產生的局部突變壓降，其中表示局部壓降損失系數，SK表示導向管底部流水孔的面積.在導向管側孔內外存在局部突變的壓降[4]可表示為

其中，C3為局部壓降損失系數[7]；ζC3是開孔的局部水頭損失系數，一般取1；nC3為導向管側孔的數目；SC3為側孔的面積.根據式(12)、(13)、(15)可得

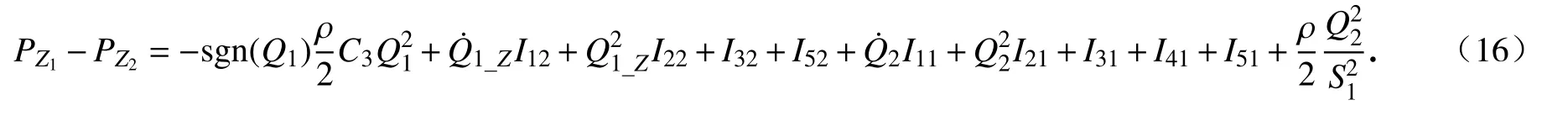
根據式(14)、(15)可得

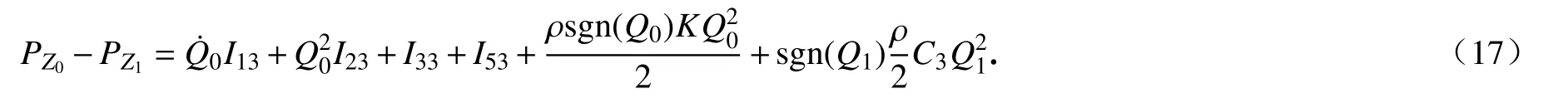
式(16)中的PZ1-PZ2表示導向管側孔外與導向管頂部外側之間的壓降；式(17)中的PZ0-PZ1為導向管底部外側與導向管側孔外之間的壓降.這兩個壓降的計算通常通過實驗求得.

式(16)與式(17)可以組成一個非線性方程組，其中的未知量有Q0，Q1，Q2.觀察圖1(a)中的四個流量及控制棒的運動速度v，根據不可壓縮條件，可以得出如下關系：

式(16)、(17)與式(1)可以組成三個方程和三個未知量的非線性微分方程組.此時可以使用將控制棒的運動和流體的流動解耦的方法求解.首先，假定控制棒運動狀態不變，計算流體流動的流量和壓強，從而得到流體阻力；然后，假定流體的流動狀態不變，根據流體阻力計算控制棒的速度和位移.計算控制棒的運動狀態時，文獻[3]采用了向前差分的方法，文獻[4-5]采用了Taylor 展開的方法.然而，這些傳統方法違背了控制棒下落運動的真實情況，只能通過不斷縮小迭代時間步長來提高精度，從而導致計算效率較低.

本文將控制棒的運動和流體的流動同時分析，即通過流-固耦合對控制棒下落進行求解.此時引入關鍵恒等變換=v，將微分方程的個數升級為四個，非線性微分方程組變為

其中

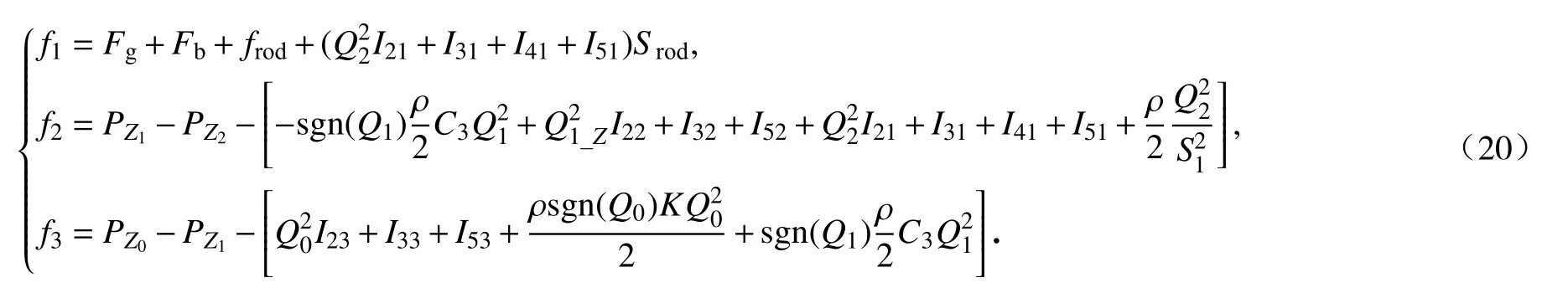
將式(19)寫成狀態方程的形式：

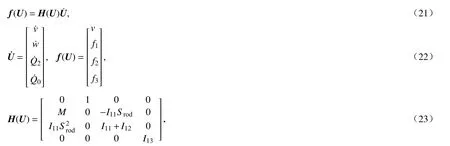
式(21)即為描述控制棒運動與導向管內流體流動的流-固耦合狀態方程，其中U為狀態向量，是待求解的未知量.當給定初始時刻的狀態向量，即可直接對上述非線性微分狀態方程進行時程積分，得到各個時間節點的狀態向量，同時得到控制棒的位移、速度、流體的流量等所有未知量.對于該方程有許多成熟算法，其中保辛算法[8-11]具有精度高和穩定性好的優點，在解決動力學[12]問題上有獨特的優勢，并在動力學的最優控制問題[13-14]、水波問題[15-16]等領域得到廣泛運用.本論文選擇辛Euler 中點格式，此部分將在后續介紹.

2.2 控制棒底部在導向管側孔之下

同理，如1.1 小節中所述，當控制棒底部在導向管側孔下方時，將導向管分成三個區間，分別為[Z1,Z2]，[Z,Z1]，[Z0,Z].

類似于上一小節的方法，可以得到如下非線性微分方程組：

其中

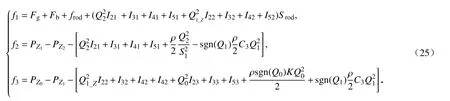
本小節與上一小節的不同主要體現在計算導向管內壓降和控制棒所受壓差阻力上.本小節中控制棒所在區間為[Z1,Z2]，[Z,Z1]，在計算區間[Z,Z1]內導向管的壓降時，需考慮控制棒所受摩擦阻力產生的壓降；同時，本小節中控制棒受到的壓差阻力需將這兩個區間上控制棒受到的壓差阻力相加.

同理，將式(24)寫成與式(21)完全相同的狀態方程，其中f1，f2和f3的表達式見式(25)，而H(U)的表達式如下：

至此，我們給出了描述控制棒下落與流體流動統一的耦合狀態方程，無論控制棒在導向管側孔上方還是下方，耦合方程的形式是相同的，即為f(U)=H(U)，不同之處在于H(U)和f(U)的表達形式.如果考慮控制棒上部分驅動桿結構和流場分析，也可表示為如式(21)所示的統一的狀態方程求解.

3 時間步長自適應保辛算法

求解式(21)所示狀態方程，本文選擇辛Euler 中點格式，在此詳細介紹.假設狀態方程(21)中t0時刻U0已知，要計算U1.將狀態方程變形為

則根據辛Euler 中點格式[9]有

其中

式(28)是一組非線性微分方程，可以迭代求解，首先假設=U0，然后按n=0,1,2,··· 開始循環：

直到與之間的相對誤差小于允許值，則停止計算，此時U1=.再以U1為初值，計算U2，U3,···.計算到臨界邊界條件的值時，結束計算.

在整個落棒過程中，導向管內的流場是非定常的，甚至出現突變，因此狀態向量的時程曲線并非光滑變化，將導致數值計算的不穩定.具體體現為迭代格式(30)在實際計算時不收斂.一般需要將時間步長取得足夠小才能保證數值計算收斂.然而在大部分時程積分區間，狀態向量的時程曲線是光滑的，時間步長并不需要取很小就可以保證收斂.綜合以上兩方面考慮，在保證整個時程分析收斂的同時，盡可能地提高計算效率，本文引入時間步長自適應算法.該方法將采用一個穩定的、較大的時間步長，記為Δt0（比如0.01 s）.因為在大部分時間段內，流場沒有突變，狀態向量變化是光滑的，因此取較大的時間步長 Δt0，可以保證迭代的收斂.當流場發生突變時，仍然取 Δt0會出現迭代格式不收斂的情況，據此可以根據迭代步數來判斷流場是否發生突變.在實際計算時，以給定的允許迭代步數Ni為依據，如果某次計算時，迭代步數大于Ni，則判斷該時間步長內，流場發生了突變，這時將時間步長減半為0.5Δt0，重新迭代.重新迭代后，如果迭代步數仍然超過Ni，則將時間步長再次減半為(0.5)2Δt0，重新迭代；如果迭代步數沒有超過Ni就收斂，則結束本次迭代，進入下個時間步計算.當給定Δt=Δt0時，在每個時間步的具體計算流程為：

1）令=U0，n=0.

2）判斷n＜Ni是否成立，如果是，計算式(30)，得到，進入步驟3）；如果否，Δt=進入步驟1）.

4）U1=，進入下一個時間步進行計算.

4 算 例

以本文建立的落棒分析模型分析某小型反應堆的控制棒下落過程，并將計算結果與在核工業長期使用的某商業軟件計算結果進行對比.整個控制棒下落組件分為上下兩個部分，這兩部分由星型架連接.其中下部分主要是24 根控制棒插入到24 根導向管中，上部分是驅動桿和驅動機構，驅動機構包括：熱套管、調節器、鉤爪、行程套筒等.小堆的主要輸入參數如表1所示.

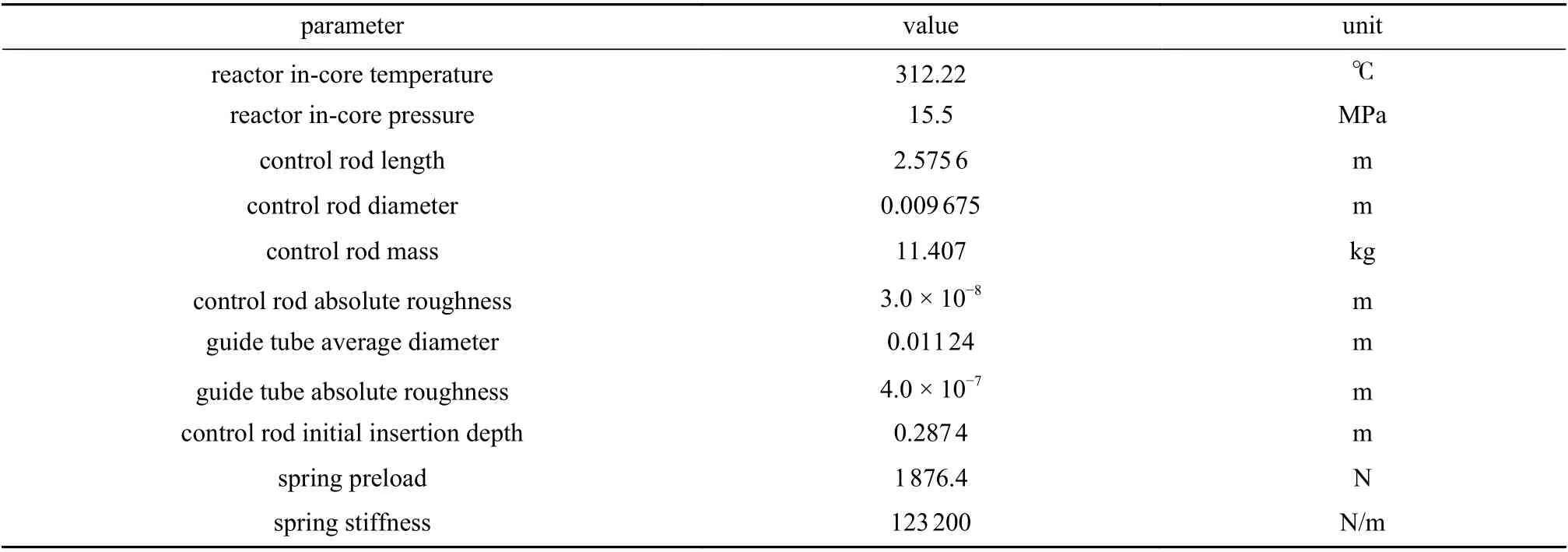
表1 小堆的主要輸入參數Table 1 Main input parameters for a small reactor

圖2所示為采用本文模型和商業軟件計算得到的控制棒在下落過程中的位移、速度和加速度的時程曲線對比圖，其中實線為本文方法的計算結果，虛線為商業軟件的計算結果.本文模型采用自適應時間步長計算，時間步長為Δt0=0.01 s ；商業軟件的時間步長為0.001 s.從圖2可以看出，本文模型采用時間步長 0.01 s計算得到的位移、速度和加速度時程曲線與商業軟件采用時間步長為0.001 s計算得到的位移、速度和加速度時程曲線高度吻合.計算結果不僅驗證了本文建立的狀態方程的正確性，且說明了本文方法的高效性.

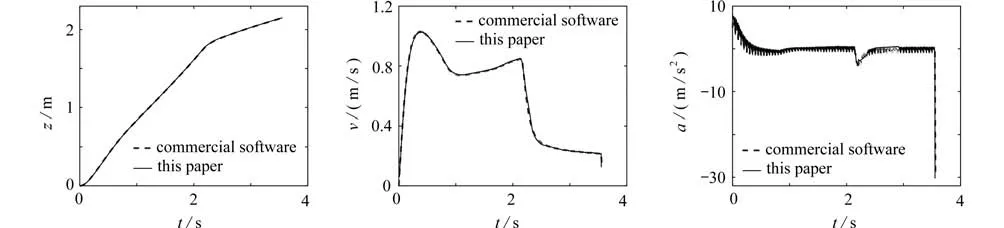
圖2 小型反應堆下本文模型與商業軟件關于位移、速度、加速度隨時間的變化對比Fig.2 The comparison of time-varying displacements,velocities and accelerations,between the proposed model and the commercial software for the case of a small reactor

以小堆為例，本文模型的初始時間步長 Δt0分別取為0.001 s，0.005 s，0.01 s，0.015 s，商業軟件的初始時間步長取為0.001 s.將本文模型得到兩個關鍵參數T5和T5+T6（T5為進入緩沖段時間，T5+T6為控制棒整體落棒時間）與商業軟件得到T5和T5+T6進行比較，結果如表2所示.

表2中，括號內的百分數表示本文模型的計算結果與商業軟件的計算結果的相對誤差.從表中可以看到，本文使用的4個時間步長所得結果與商業軟件對比，相對誤差均小于1%.本文使用的最大時間步長Δt0=0.015 s，是商業軟件時間步長的15 倍.而當商業軟件的時間步長取為0.002 s 時，計算結果發散.

表2 本文模型在不同時間步長下與商業軟件關于T5 和T5+T6的比較Table 2 The comparison of T5 and T5+T6 between the commercial software and the proposed model for different initial time steps

5 總 結

針對反應堆內控制棒下落問題，本文建立了導向管內控制棒下落和流體流動的理論模型，重點分析了控制棒受到的摩擦阻力、壓降阻力等作用力.在此基礎上，建立了描述控制棒下落與流體流動的耦合非線性方程組，再通過引入關鍵恒等變換v=，得到了流固耦合的非線性狀態方程，進一步通過高精度的辛Euler 中點格式對得到的狀態方程進行了時程分析.考慮到在不同時程分析段內導向管中流動狀態的突變，本文將時間步長自適應算法引入到時程分析中.最后以某小型反應堆控制棒下落為例進行模型和算法的驗證.算例中本文模型選取的最大時間步長 Δt0是商業軟件時間步長的15 倍，關于落棒時間T5和T5+T6的相對誤差小于1%，從而證明了本文模型和算法的正確性和高效性.本文建立的流固耦合非線性狀態方程和時間步長自適應算法不僅為控制棒下落分析提供更符合實際的計算思路，還為更加復雜的圓管內流動模型或者圓環內流動模型提供了高精度、高效率的解決方案.

致謝本文作者衷心感謝大連市“青年科技之星”項目（2018RQ06）對本文的資助.