有界多連通區(qū)域數(shù)值保角變換的GMRES(m)法*

伍 康，呂毅斌，石允龍，王櫻子

（1.昆明理工大學 理學院，昆明 650500；2.昆明理工大學 計算中心，昆明 650500）

引 言

保角變換是復變函數(shù)論中的經(jīng)典課題，可應用于流體力學、電磁理論、熱傳輸和圖像處理等，在計算復雜截面形狀的某些物理量中發(fā)揮著重要作用[1-5].保角變換的主要求解方法有解析法和數(shù)值法.解析法局限于只能在部分特殊的區(qū)域給出具體的變換函數(shù)表達式，而數(shù)值法能通過算法設計很好地逼近變換函數(shù).因此，對于那些更具一般性的實際問題，必須通過數(shù)值法計算變換函數(shù).計算保角變換的主要數(shù)值法有積分方程法、正交多項式法、有理逼近法以及有限差分法等[6-10].20世紀80年代以來，Amano 提出了基于模擬電荷法的數(shù)值保角變換計算法，用于計算將任意單連通區(qū)域內部或外部映射到單位圓內部或外部，雙連通區(qū)域映射到圓環(huán)以及多連通區(qū)域映射到部分正則狹縫域的保角變換函數(shù)[11-12].

多連通區(qū)域能通過保角變換映射到五種正則狹縫域：帶同心圓弧狹縫的圓環(huán)S(a)、帶同心圓弧狹縫的圓盤S(d)、同心圓弧狹縫域S(c)、徑向狹縫域S(r)和平行狹縫域S(p,θ)，θ是狹縫與水平正半軸的夾角，參見圖1[13].Okano 和Ogata 等成功地將有界多連通區(qū)域保角映射到了有界狹縫域S(a)和S(d)，但沒有給出將有界多連通區(qū)域映射到無界狹縫域S(c)，S(r)和S(p,θ)的保角變換函數(shù)形式[14].在上述研究的基礎上，本文研究了將有界多連通區(qū)域映射到無界狹縫域S(c)，S(r)和S(p,θ)的保角變換函數(shù)形式，補充了基于模擬電荷法的數(shù)值保角變換計算法的理論內容，同時推廣了文獻[15]的結果.本文的方法首先是將求解映射函數(shù)的問題轉化為通過模擬電荷法求解一對定義在問題區(qū)域D上的共軛調和函數(shù)g(z)和h(z)，這對共軛調和函數(shù)在D的邊界 ?D上滿足Dirichlet 邊界條件.在求解調和函數(shù)過程中使用復對數(shù)的線性組合近似g(z)，通過代入約束點和模擬電荷點得到約束方程，再用GMRES(m)法求解約束方程得到模擬電荷，獲得了高精度的近似保角變換函數(shù)，并用最大模原理進行誤差評價.提出了將有界多連通區(qū)域映射到S(c)，S(r)和S(p,θ)的數(shù)值保角變換的GMRES(m)法.

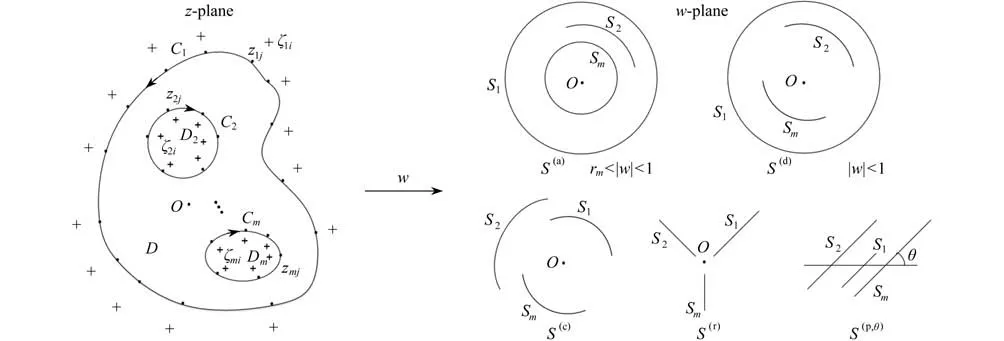
圖1 基于模擬電荷法的有界多連通區(qū)域保角變換(“·”代表約束點，“+” 代表模擬電荷點)Fig.1 The conformal mapping of bounded multi-connected regions based on the charge simulation method(“·” represents collocation points,“+” represents charge points)

本文的組織結構如下：第1 節(jié)給出了有界多連通區(qū)域映射為無界狹縫域S(c)，S(r)和S(p,θ)的保角變換函數(shù)形式和g(z)+ih(z)的近似形式，并根據(jù)邊界條件構造出約束方程.第2 節(jié)提出利用GMRES(m) 法計算約束方程.第3 節(jié)通過典型的數(shù)值實驗驗證了算法的有效性，結果顯示得到精度更高的變換函數(shù).第4 節(jié)給出了本文的結論與展望.

1 有界多連通區(qū)域映射到S(c),S(r)和S(p,θ)的數(shù)值保角變換

在z平面上，有界多連通區(qū)域D，是一個連通度為m(≥1)的區(qū)域，其邊界 ?D由m條封閉的Jordan 曲線C1,C2,···,Cm組成，區(qū)域D2,···,Dm在C1的內部是z平面內曲線C2,···,Cm圍成的單連通區(qū)域.與有界狹縫域S(a)和S(d)不同，S(c)，S(r)和S(p,θ)是w平面上的無界狹縫域.保角變換函數(shù)w(z)將邊界曲線C1,C2,···,Cm分別映射為狹縫S1,S2,···,Sm，將區(qū)域D映射為無界區(qū)域.

1.1 同心圓弧狹縫域S(c)

同心圓弧狹縫域S(c)由m條同心不同半徑的圓弧狹縫Sl和整個w平面組成，Sl的半徑為待確定的實數(shù)rl(l=1,2,···,m)，參見圖1.當保角變換函數(shù)wc(z)滿足正規(guī)化條件wc(u)=0，wc(v)=∞ 和Resz=v wc(z)=1(u,v∈D,u≠v)時(Res(·)表示取留數(shù)），可以表示如下[13]：

由Resz=v wc(z)=1，得g(v)+ih(v)=0，邊界條件可以表示為

那么g(z)是滿足Dirichlet 型場勢問題

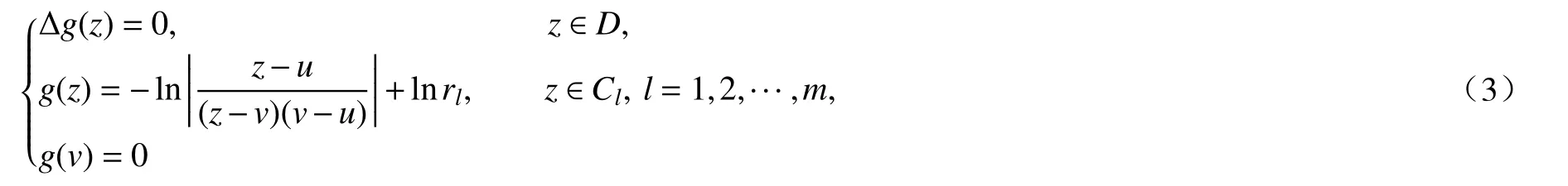
的解.

1.2 徑向狹縫域S(r)

徑向狹縫域S(r)由m條指向原點且與水平正半軸的夾角分別為待確定的實數(shù)rl的線段Sl(l=1,2,···,m)和整個w平面組成，參見圖1.當保角變換函數(shù)wr(z)滿足正規(guī)化條件wr(u)=0，wr(v)=∞ 和Resz=v wr(z)=1(u,v∈D,u≠v)時，可以表示如下[13]：

由Resz=v wr(z)=1，同樣可得g(v)+ih(v)=0，邊界條件可以表示為

那么g(z)是滿足Dirichlet 型場勢問題

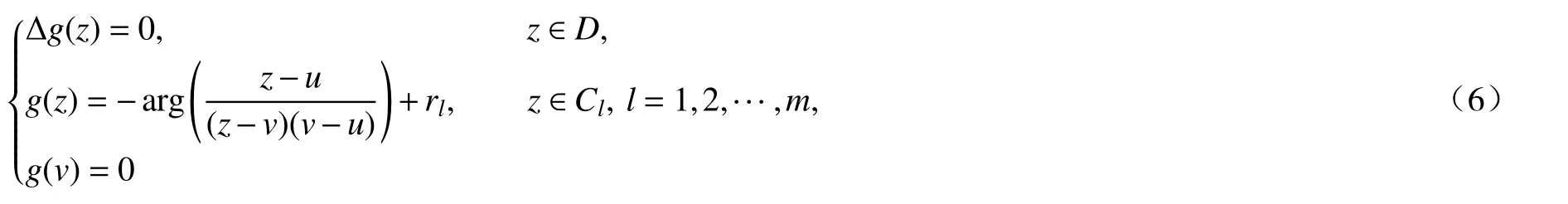
的解.

1.3 平行狹縫域S(p,θ)

平行狹縫域S(p,θ)由m條與水平正半軸的夾角為θ的平行線段Sl和整個w平面組成，Sl的位置由待確定的實數(shù)rl(l=1,2,···,m)決定，參見圖1.當保角變換函數(shù)wp(z)滿足正規(guī)化條件wp(v)=∞和 limz→v時，可以表示如下[13]：

由limz→v同樣可得g(v)+ih(v)=0，邊界條件可以表示為

那么g(z)是滿足Dirichlet 型場勢問題

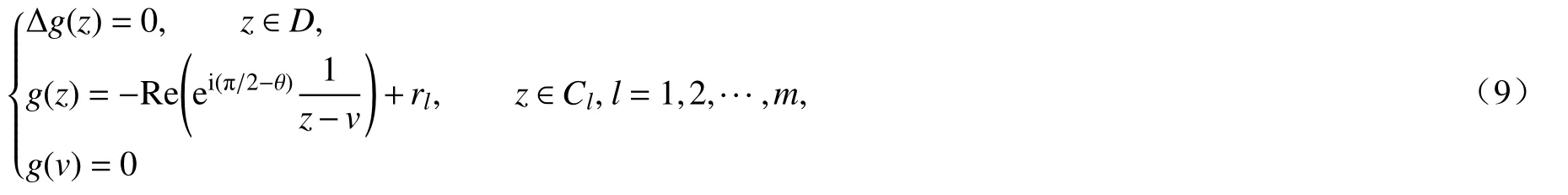
的解.

以上三種情況，h(z)與g(z)互為共軛調和函數(shù)，正規(guī)化條件都表示為g(v)+ih(v)=0，只有邊界條件表示不同.以下用W,G,H,Rl分別表示w,g,h,rl的近似值.根據(jù)模擬電荷法的原理，g(z)和h(z)可以被一個復對數(shù)函數(shù)的線性組合近似，

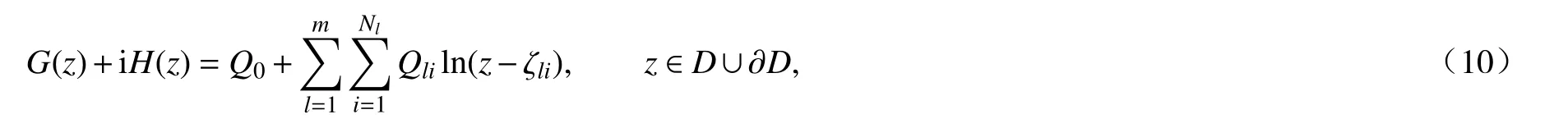
這里，ζli是配置在曲線Cl(l=1,2,···,m;i=1,2,···,Nl) 外部的模擬電荷點，未知量Q0和 模擬電荷Qli分別為復常數(shù)和實數(shù).為了實現(xiàn)上述三種類型的保角變換，該近似需要滿足以下四個條件[14].

① 邊界條件

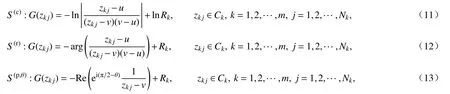
約束點zkj配置在邊界Ck(k=1,2,···,m)上，并與模擬電荷點的數(shù)量相同.

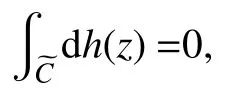
從而得

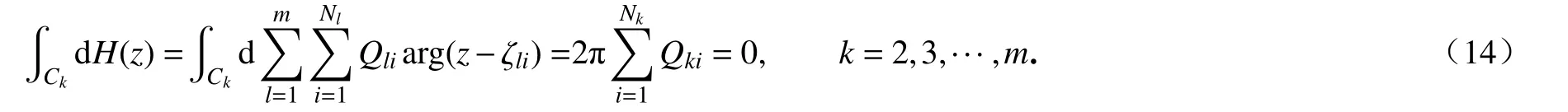
③ 根據(jù)文獻[14]和[16]，該近似形式中的Qli還需滿足

④ 正規(guī)化條件

根據(jù)式(16)，消去式(10)的Q0，得到近似形式：

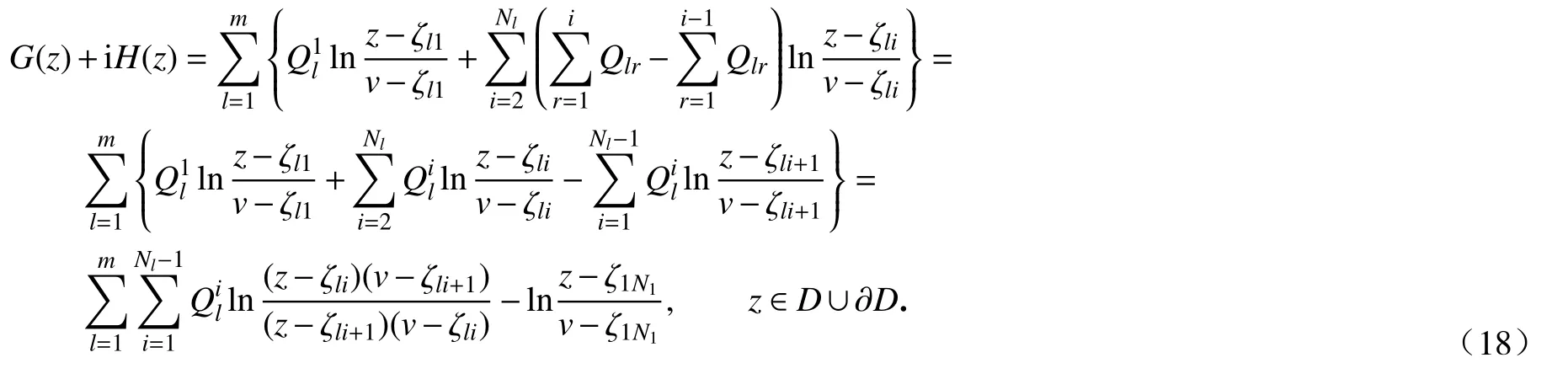
通過限制式(18)中z取Ck上的約束點zkj，并令其分別滿足邊界條件(11)～(13)，便可得到三種保角變換各自關于未知電荷Qil和Rk應該滿足的約束方程，即

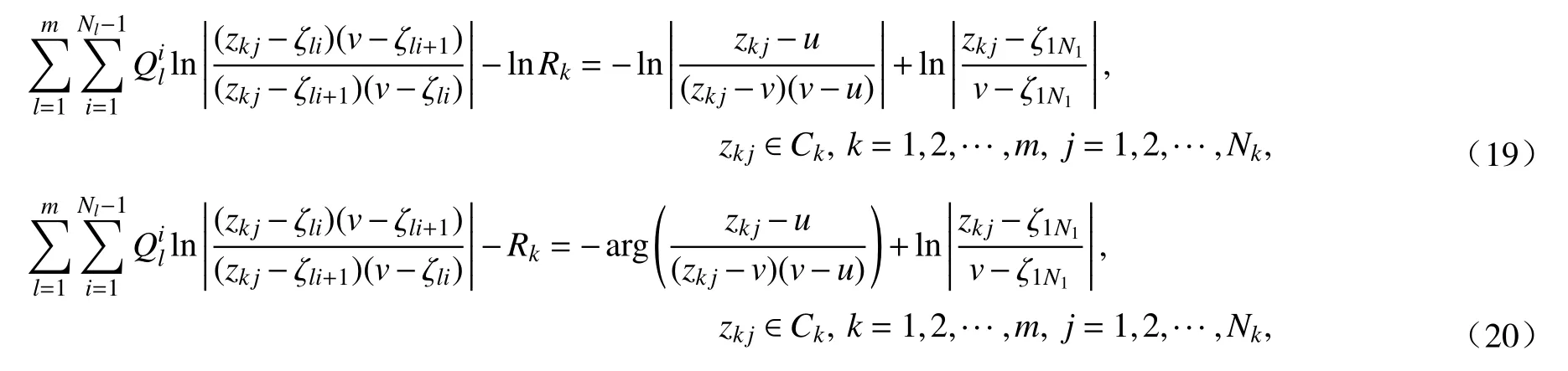
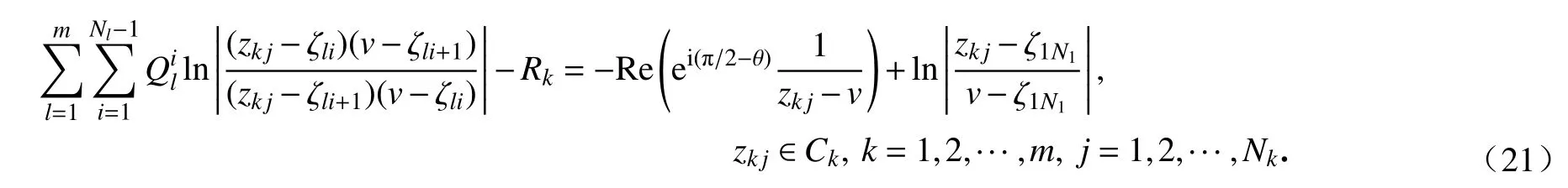
這些約束方程都構成N1+N2+···+Nm維的線性方程組，解出Qil后代入式(18)得到g(z)+ih(z)的近似，將其代入式(1)、(4)和(7)便可得到保角變換的近似函數(shù).

2 求解模擬電荷的GMRES(m)法

隨著電荷點數(shù)的增加，約束方程的系數(shù)矩陣的條件數(shù)會增大，這樣的約束方程是病態(tài)的.現(xiàn)將約束方程(19)～(21)寫成標準線性方程組Ax=b的形式，其中

A∈R(N1+N2+···+Nm)×(N1+N2+···+Nm),x∈RN1+N2+···+Nm,b∈RN1+N2+···+Nm,

A是非對稱的.m步重啟的廣義極小殘差法GMRES(m)是在Krylov 子空間

Km(A,r0)=span{r0,Ar0,···,Am-1r0}

討論求解線性方程組的方法，可以直接應用于求解系數(shù)矩陣密集且不對稱的大型線性方程組.它通過尋找近似解xm=x0+z來逼近線性方程組的準確解，其中z∈Km(A,r0)，并采用m步后必須重啟的方式避免了計算過程中計算量和存儲量過大的問題[17].其算法步驟如下：

算法1 模擬電荷的算法

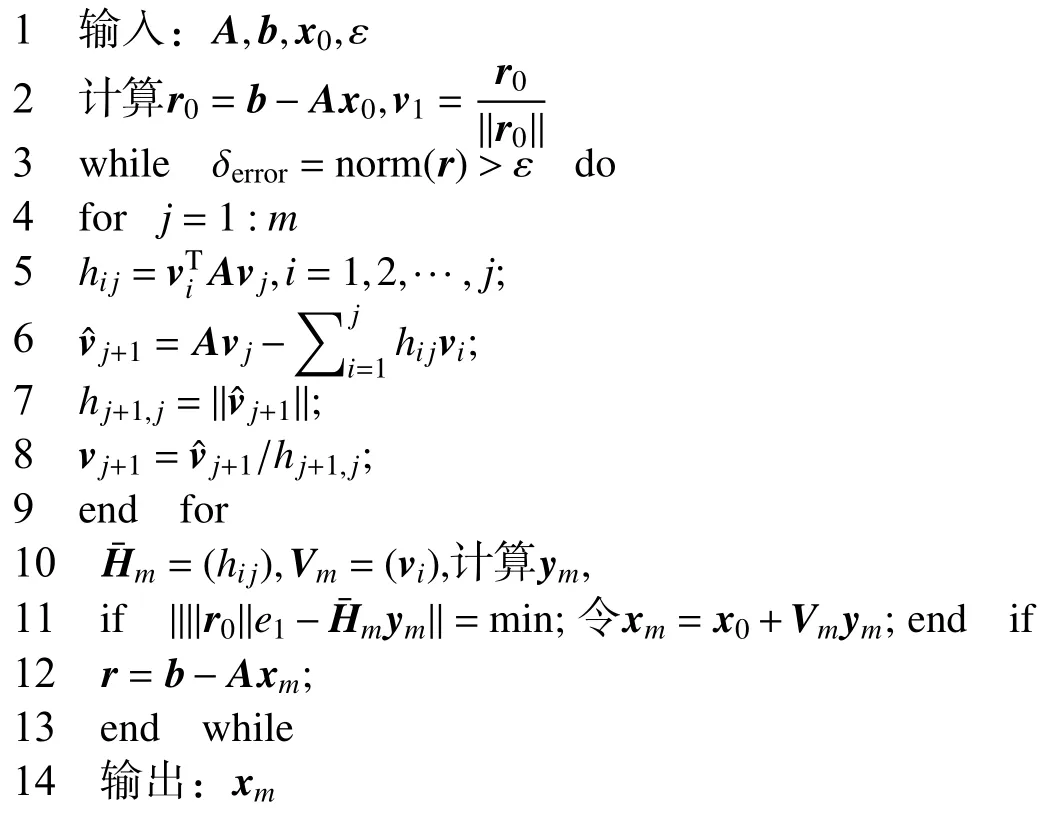
上述算法中，x0為給定的初始近似值，取為零向量，ε是允許的最大誤差.

3 數(shù)值實驗

在MATLAB 2018b的環(huán)境下，以三連通區(qū)域為例，參見圖2，其邊界曲線的方程為(x-a2)2+(y-b2)2=c22，C3:(x-a3)2+(y-b3)2=c23.利用約束方程(19)～(21) 計算保角變換函數(shù)稱為method 1，利用算法1 計算方程(19)～(21)得到保角變換函數(shù)稱為method 2.現(xiàn)用method 1 和method 2，分別對該區(qū)域到三種狹縫域的保角變換進行數(shù)值實驗，檢驗其有效性和精度，保角變換誤差由

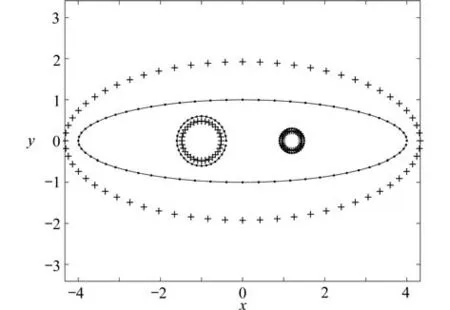
圖2 模擬電荷點ζ li和 約束點zkj的分布(N1=64,N2=32,N3=32)Fig.2 The distribution of charge points ζli and collocation points zkj,withN1=64,N2=32,N3=32

確定.表示邊界Ck(k=1,2,···,m)上任意兩個相鄰約束點的中點，且其數(shù)量與約束點數(shù)量相等.具體操作步驟如下：

步驟1設定模擬電荷點 ζli(l=1,2,···,m;i=1,2,···,Nl)和 對應的約束點zkj(k=1,2,···,m;j=1,2,···,Nk)以及其他參數(shù).

步驟2根據(jù)邊界條件(11)～(13)確定關于電荷Qil(l=1,2,···,m;i=1,2,···,Nl-1)滿足的約束方程.

步驟3求解約束方程，得到電荷Qil(l=1,2,···,m;i=1,2,···,Nl-1)，進而構造近似保角變換函數(shù)W(z).

例1a1=4,b1=1;a2=1.2,b2=0,c2=0.3;a3=-1,b3=0,c3=0.6時，根據(jù)文獻[14]，進行模擬電荷點和約束點的配置.取不同的Nl(l=1,2,3)進行實驗，圖3為邊界曲線映射后的結果.圖4是對應的誤差曲線，每幅折線圖中共有兩類六條折線，每一類的三條折線分別表示利用method 1 或method 2，將三條邊界映射為狹縫的誤差.圖中縱坐標是將誤差取10為底的對數(shù)，橫坐標表示電荷點數(shù)n.觀察可知隨著電荷點數(shù)n的增加，誤差隨之減小，當n＞160時，使用method 2的誤差曲線，在兩條邊界上的誤差明顯優(yōu)于method 1.

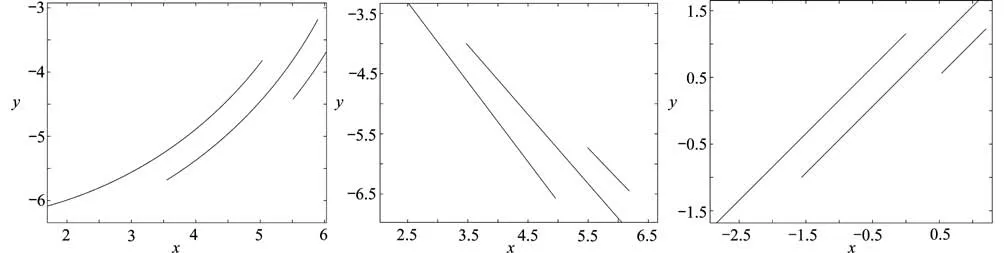
圖3 邊界保角變換為圓弧狹縫、徑向狹縫和平行狹縫(u=0,v=-0.1-0.1i,θ=π/4)Fig.3 Results of boundaries conformally mapped onto circular slits,radial slits and parallel slits,withu=0,v=-0.1-0.1i,θ=π/4

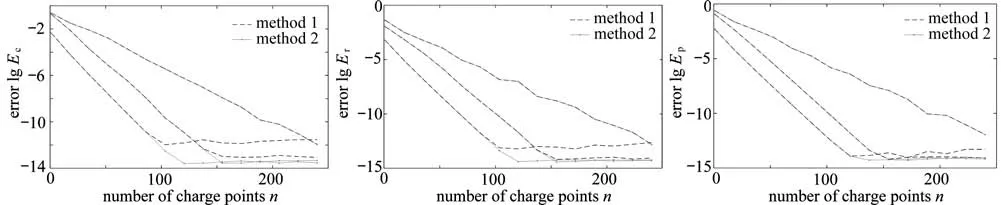
圖4 對應圖3映射到三種狹縫的數(shù)值保角變換誤差，此時(N1=N2=N3=n)Fig.4 Numerical conformal mapping errors corresponding to the mappings onto 3 kinds of slits in fig.3,with N1=N2=N3=n

圖5給出了將電荷點數(shù)調整為N1=2N2=2N3=2n時的誤差曲線，觀察可知當n＞160時，使用method 2的誤差曲線，在三條邊界上的誤差明顯優(yōu)于method 1.說明本文提出的有界多連通區(qū)域數(shù)值保角變換的GMRES(m)法可以得到更高精度的模擬電荷Qil(l=1,2,···,m;i=1,2,···,Nl-1).

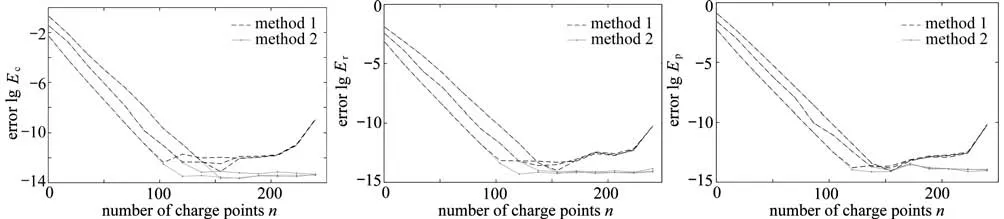
圖5 對應圖3映射到三種狹縫的數(shù)值保角變換誤差(N1=2N2=2N3=2n)Fig.5 Numerical conformal mapping errors corresponding to the mappings onto 3 kinds of slits in fig.3,withN1=2N2=2N3=2n

圖6是問題域的邊界和內部區(qū)域的網(wǎng)格，圖7～9為問題域及其網(wǎng)格映射結果的局部放大圖.可以看出近似變換函數(shù)將有界區(qū)域D成功映射為了無界的S(c)，S(r)和S(p,θ).

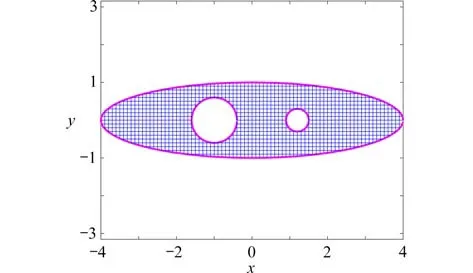
圖6 區(qū)域D 及其邊界Fig.6 Domain D and its boundaries

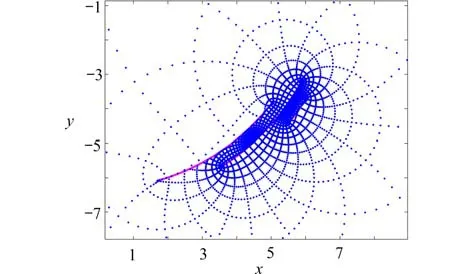
圖7 區(qū)域D 映射到圓弧狹縫域的像Fig.7 The image of domain D with circular slits

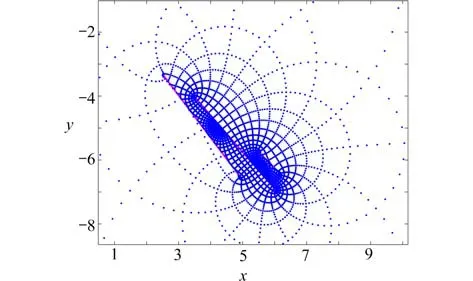
圖8 區(qū)域D 映射到徑向狹縫域的像Fig.8 The image of domain D with radial slits

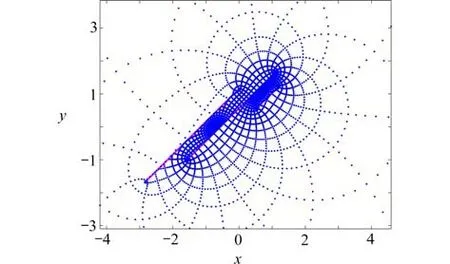
圖9 區(qū)域D 映射到平行狹縫域的像(θ=π/4)Fig.9 The image of domain D with parallel slits,whereθ=π/4

4 結 論

本文研究了將有界多連通區(qū)域映射為三種無界正則狹縫域（圓弧狹縫域、徑向狹縫域和平行狹縫域）的數(shù)值保角變換.在模擬電荷法的基礎上利用GMRES(m)法構造了上述三種狹縫域的高精度的保角變換函數(shù)，并通過數(shù)值實驗驗證了本文算法的有效性.今后我們將研究其他形式狹縫域的數(shù)值保角變換及其逆變換的算法，并將算法應用到流體力學和圖像處理等領域.