基于LiToSim平臺的疲勞壽命評估LtsFatigue軟件開發及應用*

彭夢瑤，顧水濤，周洋靖，王世猛，馮志強,3

（1.重慶大學 土木工程學院，重慶 400040；2.重慶勵頤拓軟件有限公司，重慶 401121；3.西南交通大學 力學與航空航天學院，成都 610031）

（我刊編委馮志強來稿）

引 言

工程結構在循環荷載作用下，其失效模式主要為疲勞破壞.結構疲勞破壞所受到的交變應力雖尚未達到材料屈服強度，但卻可能有瞬發性的斷裂問題，存在著巨大的安全隱患.而應用疲勞耐久性技術，可避免50%的疲勞斷裂問題，因此許多企業將疲勞耐久性定為產品質量控制的重要指標[1].

在實際應用中，汽車、飛行器及其他機械結構，大多在隨機荷載作用下工作.國內外諸多學者對其隨機疲勞問題展開了深入研究，主要工作有以下幾個部分：結構疲勞強度理論，包括常規疲勞強度設計、基于斷裂力學的疲勞強度設計、基于可靠性理論的疲勞強度設計[2]；隨機載荷的統計方法，隨機載荷不規則且無法重復，對隨機載荷只能進行統計描述，包括計數法和功率譜法兩種[3-4]；疲勞損傷累積理論，包括線性損傷累積理論和非線性損傷累積理論[5-6].目前可將隨機疲勞的分析方法歸為兩類：第一類是基于隨機過程的時間歷程曲線進行循環計數的時域法，第二類是利用隨機過程的功率譜密度(power spectral density,PSD)函數估算的頻域法.

對于時域法而言，疲勞損傷需要基于瞬態分析計算的動力響應進行時程計算.對其隨機載荷的統計，相應的計算方法包括峰值計數法、界限計數法、幅值平均計數法以及雨流計數法[7-9].其中雨流計數法具有良好的計算精度，被認為是疲勞損傷分析結果好壞的基準[10].然而，時域法的疲勞計算精度常常受到時距模擬時間長短的影響，只有通過足夠長的樣本時距以減小時域模擬中的誤差.對于復雜結構，樣本時距的增加將會大大提高計算時間[11-12].就其計算效率而言，時域法不能夠滿足工程實際需求.

盡管時域法計算結果準確，但其計算成本較大且計算精度受到樣本時距的影響.與時域法相比，頻域法通過疲勞危險點位置的應力響應PSD 計算隨機載荷引起的疲勞損傷，能夠有效減少計算工作量，是設計人員預測結構疲勞損傷的較好選擇.但是，頻域法的計算精度依賴于經驗公式的準確性，現有經驗方法包括：窄帶法、Dirlik 疲勞損傷公式、Z-B 法疲勞損傷公式、T-B 法疲勞損傷公式等[13-17].若能選擇適當的頻域計算公式使得疲勞計算精度滿足要求，則可以避免時域法的計算效率缺陷，因此頻域法具有良好的應用前景.

隨著計算機技術和有限元技術的發展[18]，國內外出現了多款疲勞分析軟件，如Fe-Fatigue（英國）、Fesafe（英國）、MSC-Fatigue（美國）、Ncode（英國）、WinLIFE（德國）、ProEMFAT（中國）等系列軟件.上述軟件功能強大，但隨機載荷的頻域算法尚不完善，除了Ncode、Fe-safe 可進行頻域疲勞分析的工作外，其余軟件暫未發展這方面的功能.為此，本文以開發定制化疲勞軟件LtsFatigue為目標，基于國內自主CAE 軟件開發平臺LiToSim，嵌入隨機疲勞數值分析程序，集成疲勞時域算法、頻域算法到有限元計算框架中，形成一套完整的疲勞求解計算程序，彌補了頻域算法在常見疲勞軟件中的空缺，同時利用LiToSim 強大的前后處理開發接口，可實現用戶界面友好、可視化效果豐富、隨機疲勞問題高效處理的定制化疲勞軟件LstFatigue的開發.

1 疲勞損傷及壽命預測理論基礎

1.1 時域法疲勞分析

結構疲勞是指結構在循環荷載作用下裂紋形成與擴展的過程.時域法通過結構動力計算得到疲勞危險點位置的應力響應時程，進而使用時域雨流計數法對時程數據處理得到危險點處的應力循環特性，包括應力循環幅值和每個幅值所對應的循環均值、循環次數.雨流計數法詳見文獻[9].

通過雨流計數法獲得的結果與材料S-N(stress-life) 曲線公式相結合，可實現結構疲勞壽命預測.S-N曲線通常由大量實驗數據擬合得到，其中常用的冪次表達式如式(1)所示，C，k均為材料參數.若構件在等幅應力S作用下，循環至破壞疲勞壽命N：

由于實驗得到的S-N曲線往往是通過零均值加載得到的，因此雨流計數法統計得到的應力循環特性需要考慮平均應力的影響[19]，可采用Goodman/Gerber 等方法修正：

式中，Sm表示實際應力循環應力均值，Su表示極限強度，Sa表示實際應力循環幅值，Sa(-1)表示零應力均值的等效循環幅值且應用于S-N曲線進行疲勞壽命估算.當p=1時，式(2)為G oodman 修正公式；當p=2時，式(2)為Gerber修正公式.

疲勞損傷通常采用Miner 線性損傷累積準則計算.結構在變幅應力Si作用ni次循環下的損傷為di，若在l個應力幅值Si作用下各經歷ni次循環，則其疲勞總損傷D為

結構疲勞壽命Nf指結構在疲勞破壞前所經歷的應力循環次數，變幅加載的隨機疲勞可根據累積疲勞損傷計算.由于結構在非危險點位置的疲勞壽命數值較大（10的冪次方），為簡化顯示結果，以10為底的對數形式l gNf表示：

時域法采用雨流計數對時程曲線進行準確計數，計算精度高.但時域法依賴于樣本時距的長短，由于雨流計數法需要對每個數據進行處理，樣本時距將對計算效率產生影響.對工程實際結構進行疲勞分析，需要在滿足計算精度要求的同時有效提高計算效率[10].

1.2 頻域法疲勞分析

頻域法通過隨機振動理論獲得結構疲勞破壞控制點處的應力響應PSD，利用頻譜參數等確定應力循環分布的概率密度函數，依據S-N曲線及Miner 線性損傷累積準則及經驗公式來估算疲勞損傷，其核心在于估算應力幅值的概率密度函數.由Miner 線性準則和應力幅值的概率密度間的關系，可將疲勞損傷的期望率E(D)表示為[20]

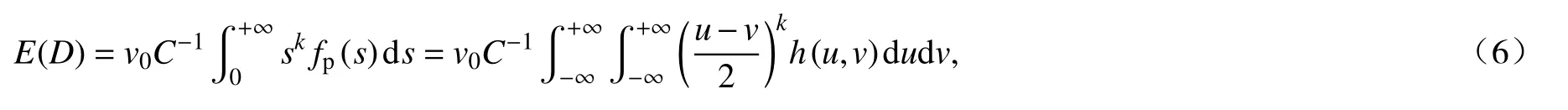
式中，穿零率v0為單位時間的循環總數；C，k為S-N曲線材料參數；s表示應力幅值；fp(s)為其概率密度函數；u，v分別為峰值和谷值，h(u,v)為其聯合概率密度.

疲勞總損傷D可由疲勞損傷的期望率E(D)表示為

式中，T為樣本時距；E(D)為疲勞損傷期望率，即單位時間疲勞損傷.頻域法結構疲勞壽命及壽命對數可由式(7)與式(4)、式(5)聯立求解得到.

由于應力循環的響應統計特性不同，可依據帶寬參數（α1，α2）和統計參數（均值Sm、標準差σX、偏度Sk、峰度Ku）將隨機過程分為窄帶Gauss 隨機過程、寬帶Gauss 隨機過程、非Gauss 隨機過程[21].

1.2.1 窄帶Gauss 隨機過程

窄帶Gauss 隨機過程應力幅值s的概率密度函數fp(s)近似服從Rayleigh 分布：

式中，σ2X為隨機過程的方差.

1.2.2 寬帶Gauss 隨機過程

寬帶Gauss 隨機過程計算疲勞損傷的應力幅值概率密度函數較復雜，若仍采用窄帶Gauss 過程的Rayleigh 分布假設，將會高估疲勞損傷率，需要找出更合理的應力幅值（或范圍）概率密度函數[22].T-B 譜方法提出一種線性組合近似計算：

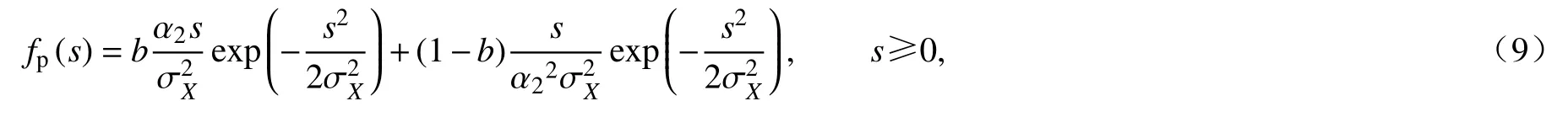
其中，b為組合參數，α1，α2是由譜矩表示的帶寬參數，且1＞α1＞α2＞0，當α1=α2=0 時為白噪聲，α1=α2=1時為嚴格的窄帶隨機過程.參數b的選擇主要通過大量模擬實驗擬合得到.文獻[17]提出b可由帶寬系數 α1和α2表示為

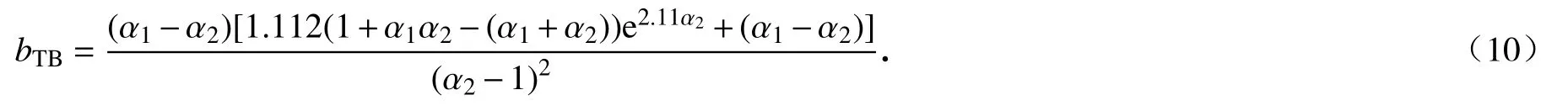
Ding 和Chen[23]基于T-B 法改進為D-C 譜方法，通過數據擬合的方式給出了更簡化的參數b的形式：

參數b與響應譜形狀相關，選擇不同經驗公式將直接影響頻域疲勞分析的計算精度.

1.2.3 非Gauss 隨機過程

式中，hGRF(xu,xv)為Gauss 過程中的雨流計數法所得峰值谷值概率分布函數，同時可表示為

其中，hGLC(xu,xv)為界限計數法(LC 法) 計算得到的峰值谷值聯合概率密度函數，hGRM(xu,xv)為范圍計數法(RM 法)計算得到的峰值谷值聯合概率密度函數[23]：

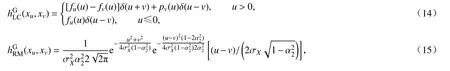
結構疲勞分析流程如圖1所示.

圖1 結構疲勞分析流程Fig.1 The structural fatigue analysis process

2 LtsFatigue 疲勞分析軟件構建

基于LiToSim 平臺，嵌入含時域、頻域算法的疲勞分析數值計算程序，定制化開發一款LtsFatigue 疲勞軟件.

2.1 LiToSim 平臺簡介

LiToSim是一款采用C++語言、面向對象編程思想及通用數據標準研發的有限元軟件共性開發平臺.具有數據處理、圖形交互和項目管理等諸多功能，能夠為用戶高效地開發專用CAE 軟件提供支持[18].

LiToSim 定制化層包括專業模塊和專業軟件求解器兩部分[24].專業模塊提供專業的CAE 軟件開發所需的前/后處理功能模塊及相關接口；專業軟件求解器提供常規問題通用求解器和特定問題相關定制求解器接口[25-28].LiToSim 平臺架構如圖2所示.

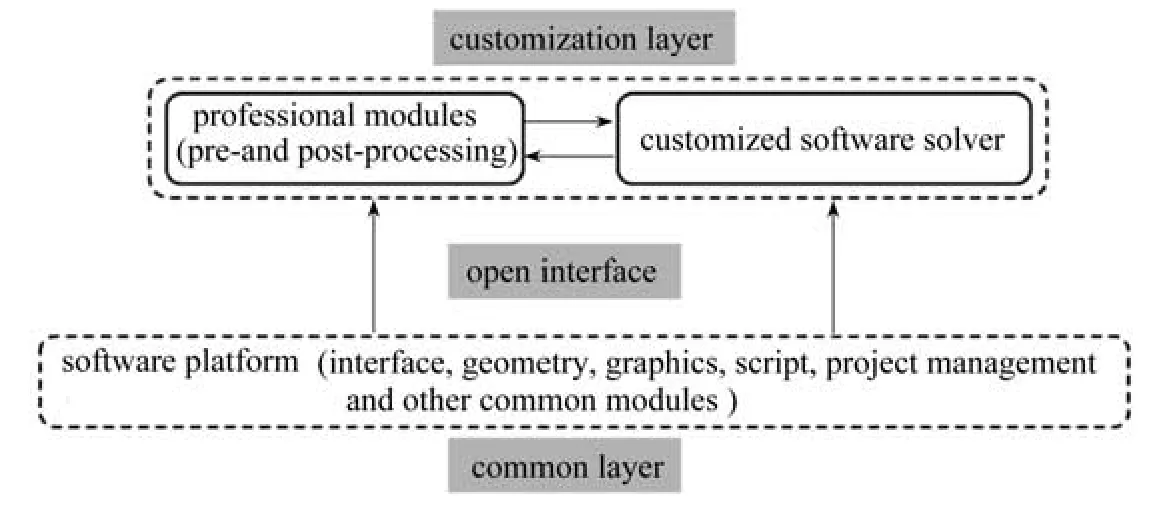
圖2 LiToSim 平臺架構圖Fig.2 The LiToSim platform architecture diagram

2.2 LtsFatigue 疲勞軟件組織結構

基于LiToSim 已有的通用前處理、求解器模塊及其開放接口，定制化開發疲勞分析軟件LtsFatigue.如圖3所示，疲勞分析所需新增的模塊包括計算模型、材料參數及疲勞算法模塊三個部分，同時新增針對疲勞分析的后處理結果顯示.

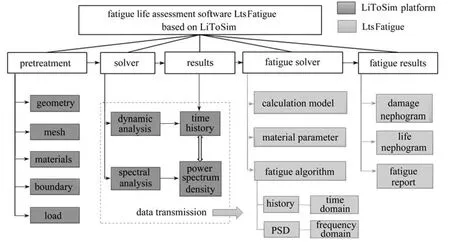
圖3 基于LiToSim的定制化疲勞軟件LtsFatigue 組織結構圖Fig.3 The organizational structure of the LiToSim software fatigue module (LtsFatigue)

針對疲勞各子模塊的功能應用，設計LtsFatigue 軟件的界面便于用戶操作.如圖4所示，界面可主要分為三個部分，包括計算模型、材料參數、疲勞算法及結果后處理模塊.

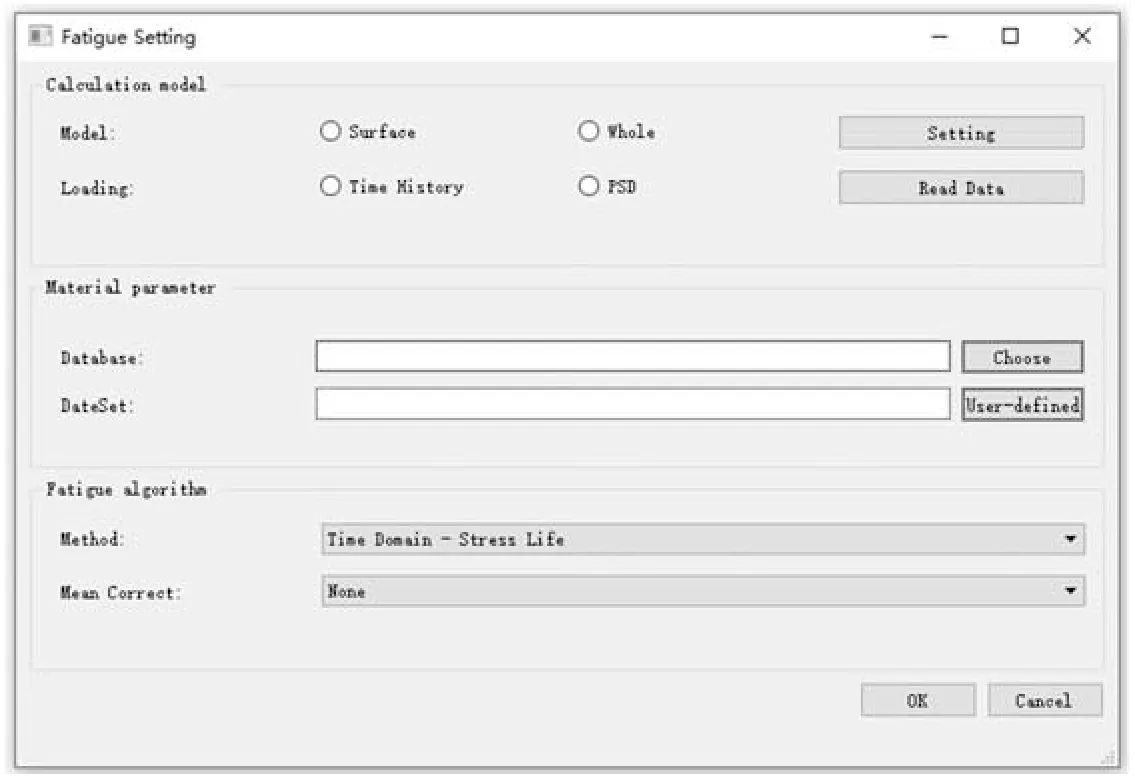
圖4 基于LiToSim的定制化疲勞軟件LtsFatigue 界面Fig.4 The interface for customized software LtsFatigue based on LiToSim

2.2.1 計算模型模塊

LtsFatigue 軟件與LiToSim 有限元分析軟件直接連接集成，依賴于有限元軟件的計算結果.在LiToSim 軟件完成結構動力計算后，通過界面操作導入模型整體或表面的節點、單元網格信息及其應力響應結果，同時選擇載荷類型為時程序列或PSD.

2.2.2 材料參數模塊

LtsFatigue 軟件的材料庫提供常用鋼材、鋁合金的疲勞性能數據，主要包括一般材料數據信息如彈性模量E、Poisson 比v、S-N曲線、E-N曲線、疲勞強度指數b、疲勞強度系數sf等數據.用戶在如圖5所示的主界面材料模塊點擊按鈕，可對這些數據進行自定義編輯、圖形繪制等操作.

2.2.3 疲勞算法模塊

對于導入應力響應時間歷程結果的疲勞計算，提供基于應力-壽命的時域疲勞算法.對于導入應力響應PSD 函數的疲勞計算，提供基于應力-壽命的頻域疲勞算法.

此外，該模塊提供多種平均應力修正方法，包括Goodman、Gerber 等修正公式.其中，時域法對雨流計數法計算得到的多個應力循環逐一進行平均應力修正，頻域法對應力響應PSD 函數的整體平均應力進行修正.

2.2.4 疲勞結果后處理模塊

LtsFatigue 后處理模塊可分別對節點、單元的計算結果繪制疲勞損傷、疲勞壽命云圖等，同時用戶可在圖6所示的界面中選擇幾何表面、幾何體、邊緣單元等多種方式查閱疲勞分析結果.

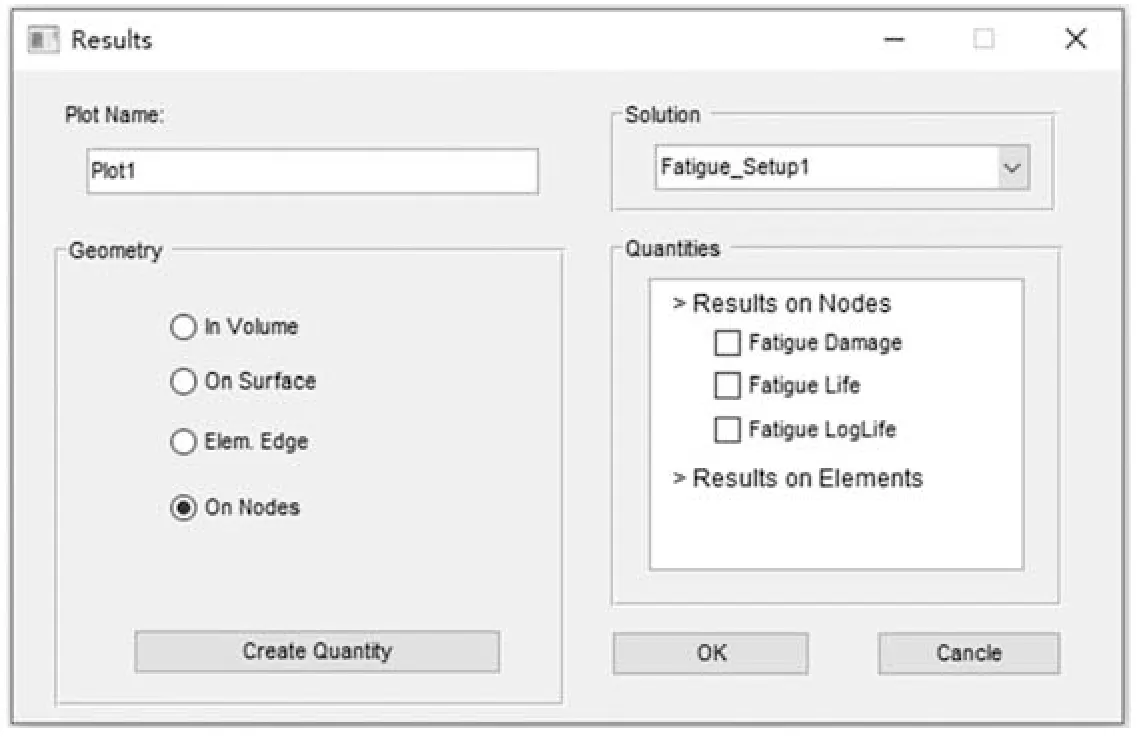
圖6 疲勞結果繪制Fig.6 The fatigue results plot

2.3 LtsFatigue 疲勞分析操作流程

LtsFatigue 疲勞軟件依賴于有限元分析結果，需要先通過LiToSim 完成結構模型的建立、材料參數的定義、邊界條件的設置、結構網格劃分等流程，并進行結構動力計算輸出應力響應數據.然后在LtsFatigue 疲勞軟件界面中的計算模型模塊提取有限元結果，材料模塊定義材料參數，疲勞算法模塊選擇疲勞算法及平均應力修正公式.通過LtsFatigue 界面操作完成上述設置，進行疲勞分析計算，其界面圖見圖4、流程圖見圖7.

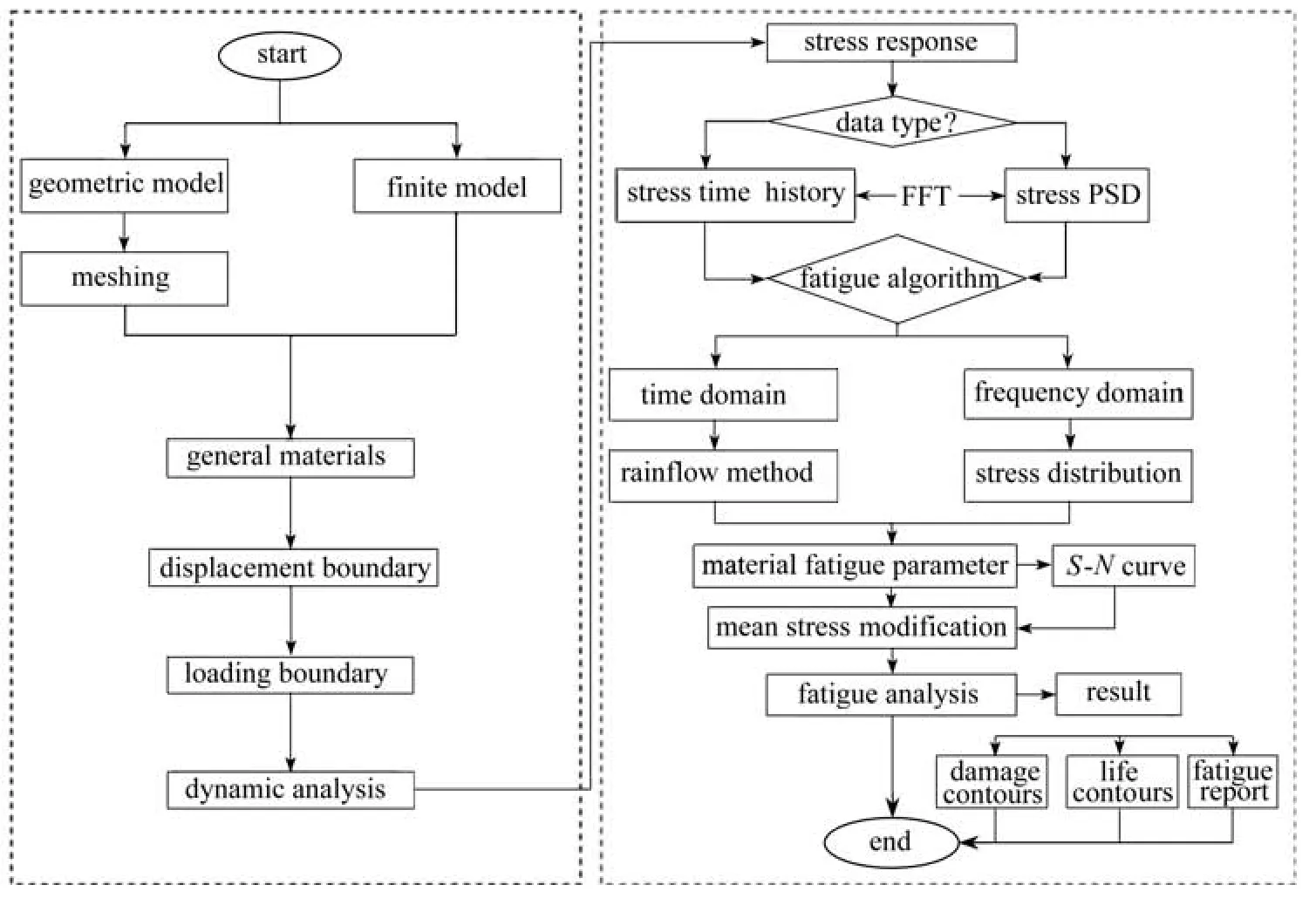
圖7 基于LiToSim的定制化疲勞軟件LtsFatigue 分析流程Fig.7 The analysis process of customized software LtsFatigue based on LiToSim

3 LtsFatigue 軟件數值算例

齒輪構件應用廣泛，其疲勞問題突出.本文以齒輪構件為例，鋼材選擇Q345 鋼，屈服強度345 MPa，極限拉伸強度500 MPa.

幾何參數：齒數為20，模數為2.75，如圖8所示.材料特性：彈性模量為2.1×105MPa，Poisson 比為0.33.疲勞參數：疲勞強度系數sf=600 MPa，疲勞強度指數b=-0.095，材料S-N曲線（S為應力幅值，N為S幅值循環的疲勞壽命）公式滿足

圖8 齒輪示意圖Fig.8 Schematic diagram of the gear

邊界條件：齒輪中心圓孔固定約束，圓環表面受到隨機載荷.

為探究自主開發的疲勞軟件LtsFatigue的計算優越性，對齒輪算例進行疲勞分析，以大型商業軟件ABAQUS聯合Fe-safe 計算結果為基準，從疲勞計算精度、計算效率兩方面探究LtsFatigue 軟件所具有的優勢.

齒輪受到的疲勞荷載為一組樣本時距長度4 000 s的隨機載荷，采樣頻率10 Hz.最后載荷步的有限元計算結果見圖9，第一主應力最大的節點9018(14 mm,-6.93 mm,0.99 mm)，所在位置被認為是疲勞危險點之一.國內自主CAE 軟件LiToSim的有限元分析結果與商業軟件ABAQUS 計算結果一致，這說明定制化疲勞軟件LtsFatigue 基于LiToSim 平臺進行開發可靠有效.

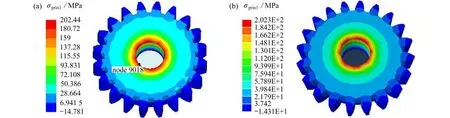
圖9 有限元分析結果，第一主應力對比：（a） LiToSim 有限元分析結果，第一主應力；（b） ABAQUS 有限元結果分析結果，第一主應力Fig.9 For finite element analysis (FEA) results,the comparison of the 1st principal stress: (a) LiToSim FEA results; (b) ABAQUS FEA results

疲勞危險位置節點9 018的應力響應時程曲線見圖10，該組數據的統計特性如表1所示，該點的應力響應時程為弱非Gauss 寬帶隨機過程，其疲勞分析在時域可采用雨流計數法，在頻域可選用D-C 譜方法估算齒輪結構的疲勞壽命.

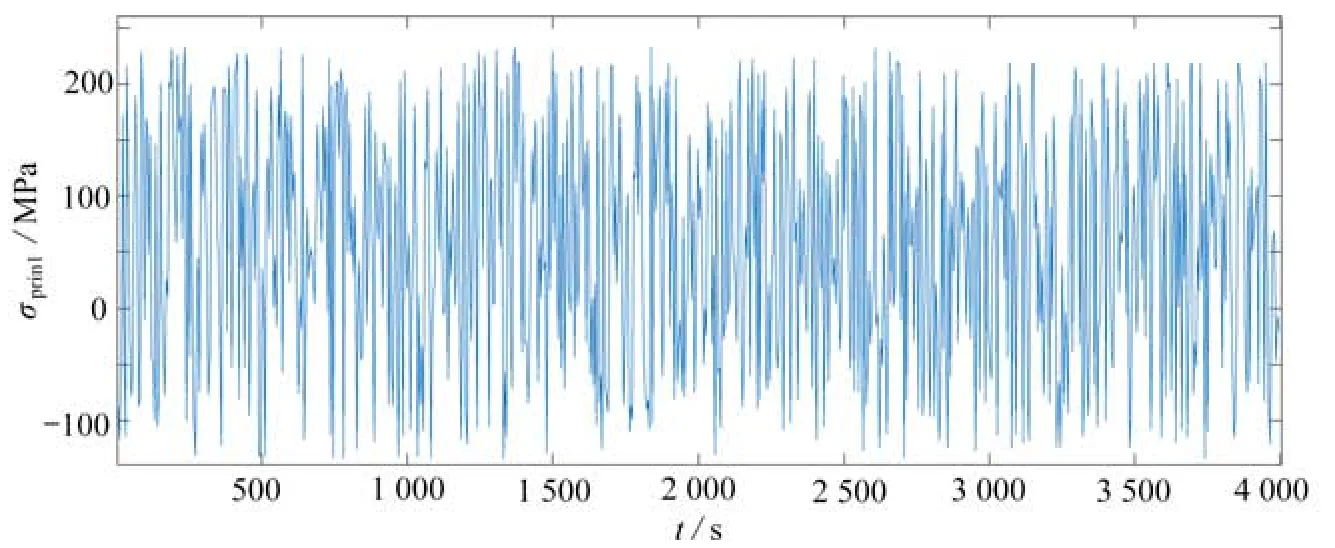
圖10 節點9 018 應力響應時程曲線Fig.10 The time-history curve of stress response at node 9 018

表1 應力響應統計特性Table 1 Stress response statistical characteristics

3.1 算例1：時域法疲勞分析

對于時域疲勞分析，采用雨流計數法對應力響應準確計數.LtsFatigue 軟件計算的齒輪構件疲勞損傷、疲勞壽命云圖見圖11(a)，Fe-safe 聯合ABAQUS 軟件計算的疲勞壽命云圖見圖11(b).對比結果可知，Fe-safe 計算得到的齒輪最危險位置的疲勞壽命（l gNf）為0.934 3，LtsFatigue 計算得到的疲勞壽命（l gNf）為0.938 1，結果相差約1%，軟件計算精度滿足要求.

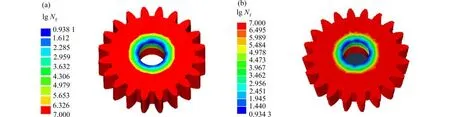
圖11 LtsFatigue 與Fe-safe 時域疲勞壽命對比：（a） LtsFatigue 疲勞壽命結果，時域法；（b） Fe-safe 疲勞壽命結果，時域法Fig.11 Comparison of the fatigue life between LtsFatigue and ABAQUS/Fe-safe time domain: (a) the LtsFatigue fatigue life-time domain;(b) the Fe-safe fatigue life-time domain

3.2 算例2：頻域法疲勞分析

對于頻域疲勞分析，采用應力循環分析函數的經驗公式估算疲勞損傷，可通過Fourier 變換將應力響應時程轉換為PSD.以LtsFatigue 內置D-C 譜方法為例，將時域疲勞結果作為基準，驗證頻域算法的準確性.從LtsFatigue 疲勞壽命云圖（圖12(a)為時域結果，圖12(b)為頻域結果）對比來看，頻域算法計算結果與時域結果相差約3%，計算精度基本滿足要求.同時，表2結果表明LtsFatigue 應用頻域算法估算疲勞壽命，計算效率提高約45%.分析其原因在于頻域法通過概率分布函數替代了時域法中雨流計數法對隨機過程的處理，使得疲勞分析過程有效簡化.頻域法與時域法二者精度相當，但頻域法在效率上有明顯優勢，因此對于復雜結構的隨機疲勞分析問題，應用頻域疲勞算法具有重要意義.

表2 LtsFatigue 與Fe-safe 計算精度和計算效率對比Table 2 Comparison of computational accuracy and computational efficiency between LtsFatigue and Fe-safe

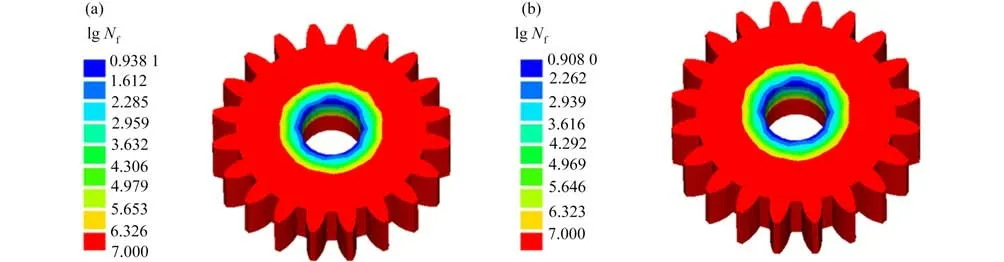
圖12 LtsFatigue 時域與頻域疲勞壽命：（a） 時域法；（b） 頻域法Fig.12 LtsFatigue time domain and frequency domain fatigue lives: (a) the fatigue life-time domain; (b) the fatigue life-frequency domain

4 結 論

本文將基于應力時間歷程的時域疲勞算法與基于應力PSD的頻域疲勞算法嵌入有限元分析框架，充分利用LiToSim 平臺的開放接口，形成了一款疲勞分析定制化軟件LtsFatigue.通過對齒輪算例疲勞分析，驗證了LiToSim 平臺有限元分析結果的可靠性，對比了定制化軟件LtsFatigue的時域算法、頻域算法計算精度與大型商業軟件ABAQUS 聯合Fe-safe 結果相差約3%，同時頻域算法將計算效率提高約45%.針對復雜結構的疲勞模擬分析，在保證計算精度的前提下，頻域算法是提高計算效率的重要工具.基于LiToSim 平臺的疲勞分析定制化軟件LtsFatigue，為國內自主研發軟件提供了一條新思路.