射流通道內方柱發熱器件的幾何設計*

饒 凱，謝志輝，關瀟男，孟凡凱，戈延林

（1.海軍工程大學 動力工程學院，武漢 430033；2.武漢工程大學 熱科學與動力工程研究所，武漢 430205；3.武漢工程大學 機電工程學院，武漢 430205）

引 言

隨著電子技術的發展，電子器件的性能不斷提升，其散熱需求日益增強，流體冷卻方式成為突破該類散熱瓶頸的重要技術手段之一[1-4].研究發現，發熱器件的間距和長度變化對器件散熱性能有重要影響[5-6].在電子系統中，常常包含一個或幾個高散熱組件，一種解決其散熱問題的可行方法是采用T 形通道射流冷卻，即將冷卻流體由垂直通道射入，通道射流入口被設置在高散熱部件上方，橫流則為其他需要較低冷卻能力的器件提供均勻的冷卻環境.Rundstroem 等[7]研究了沖擊射流的Reynolds 數、橫流的Reynolds 數以及頂板與底板之間的距離對流場的影響，其中停滯點、分離、回流和曲率效應等與流動相關的因素會影響傳熱速率和壓降.Meghdir 等[8]以有限體積法為基礎，研究了電子元器件在氣流通道中受到沖擊射流時，電子元器件的幾何形狀對冷卻效率的影響.此類散熱解決方案不會直接增加電子器件的重量、體積和成本，但能提升裝備的可靠性.

熵產反映了傳熱過程的不可逆耗散，Bejan[9-10]推導了有限壓差流體流動和有限溫差傳熱的熵產率公式，并應用在傳熱過程優化中，由此提出了熵產生最小化原理.Rehman 等[11]對具有新型側壁肋片結構的微通道散熱器內的流體傳熱特性進行了數值研究，發現水翼型側壁肋條可使系統熵產率最小.Pati 等[12]對高Prandtl 數流體層流強迫對流作用下圓管壁面熱流的非均勻分布進行了數值研究，與均勻加熱相比，該加熱策略產生的熵產率和峰值溫度更小.Kingston 等[13]利用基于速率分布的Taylor 和Krishna 模型，研究了低壓填料蒸餾塔中的空氣分離規律，通過數值優化確定了使系統熵產率最小的換熱溫度分布.

Bejan 研究了各種自然樹狀網絡結構生成的普遍物理機制，發現了構形定律，提出了構形理論，為熱設計優化開辟了新的途徑[14-19].構形定律可簡要表述為：事物結構源自于性能達到最優[16].Mustafa 等[20]在固定壓降條件下，自由改變大管間距和小管軸長，以系統最大換熱密度為優化目標，以大管間距為約束條件，對二維通道橫流中的雙尺度菱形管進行了構形優化.Abbas 等[21]對縱向翅片管的三種布置方式：前翅片、后翅片和等寬度前、后翅片進行構形設計，實現了從翅片管到通道橫流的熱流密度最大化.Ahmed 等[22]以管的垂直軸長和管間距為優化變量，以系統最大換熱密度為優化目標，以管的高度和管的水平軸長為約束條件，對二維通道中的單排菱形管進行了構形優化.Yu 等[23]設計了一種新型的構形分支回熱器，研究了不同絲網傾斜角對回熱器熱力特性的影響.Gong 等[24]以變截面圓柱體熱源為研究對象，進行了以無量綱熱點溫度最小為目標的構形優化.范旭東等[25]以變物性條件下圓柱體熱源為研究對象，進行了以火 積當量熱阻和最大熱阻最小化為目標的構形優化.王剛等[26]建立了圓柱體熱源的三維湍流散熱模型，研究了導熱系數、熱源強度和流體流速對器件最高溫度、火 積當量熱阻和平均Nusselt 數的影響.Teixeira 等[27]在強迫對流條件下，以熱源間縱向和橫向距離與自身尺寸的比值為優化變量，以熱源的橫截面積和熱源排列的占用面積為約束條件，以系統阻力系數最小為優化目標，對二維通道中按照三角形排列的方形鈍體熱源進行了構形優化.Aghenese 等[28]以最大化Nusselt 數和最小化氣缸與周圍流動之間的阻力系數為優化目標，以圓柱橫向間距與圓柱直徑之比為優化變量，以四個圓柱的總體積為約束條件，對四個交錯排列的圓柱熱源模型進行了構形優化.Razera 等[29]以橢圓柱之間的垂直距離和橢圓柱的長短軸比為優化變量，通過改變流體的壓力差，以橢圓管的橫截面面積為約束條件，以換熱密度最大化為優化目標，對二維通道中的橢圓柱熱源進行了構形優化.Wang 等[30]以無量綱熵產率最小為優化目標，以導熱系數分布與熱源強度分布為優化變量，以熱源總發熱功率和各熱源導熱系數之和為約束條件，分別得到了橢圓柱離散熱源的最優熱源強度分布和最優導熱系數分布.

在給定約束條件下，通過研究事物外形和結構的演化與性能變化的規律以獲得最優設計結果，是工程構形設計的核心思想[15-19].前述研究的熱源均采用單入單出橫向對流冷卻的方式，本文采用單入雙出射流冷卻的方式，結合熵產生最小化原理和構形理論，以熱源總縱截面面積和熱源高度一定作為約束條件，以系統最高溫度和熵產率最小為優化目標，以離散熱源之間的長度比為優化變量，對射流通道內的方柱離散熱源進行幾何設計，研究射流速度、熱源大小和位置分布對系統最高溫度和熵產率的影響，可為實際發熱器件的熱設計提供理論指導.

1 數理模型和求解方法

1.1 幾何模型

圖1給出了二維T 形通道內方柱熱源的幾何模型，圖2為整體網格圖.其中熱源處于一水平的矩形通道中，水平通道高為H，導熱基座長度和厚度分別為L=4H和Hb=0.03H.通道上方有一矩形射流通道，其口徑與水平通道長度L的比值為=0.1，射流速度為Uj.在基座中軸線上布置3個離散熱源（如圖1所示，編號為1，2，3），其中熱源長度為di=0.1L，高度為h=0.2H，熱源中點之間的距離從左至右依次為L1到L4，且

圖1 熱源幾何模型圖Fig.1 The geometric model for heat sources

圖2 整體網格圖Fig.2 The overall grid pattern

設三個方柱熱源的高度相等，且d1=d3，L2=L3，有熱源長度比

熱源之間的間距與通道總長度的比值為

構形設計的幾何約束為離散熱源的縱截面面積A和熱源高度h一定，即

將式（2）代入式（4），可得到

離散熱源為均勻產熱，熱源的總產熱率給定，3個離散熱源的熱源強度均相等.

在式(1)～(5)的幾何約束條件下，以熱源之間的長度比β為優化變量，以系統最高溫度和熵產率最小為優化目標，對二維T 形通道內方柱熱源進行構形優化.

1.2 傳熱模型

導熱基底材料為硅（定壓比熱容cp=700 J·kg-1·K-1，密度ρ=2 329 kg·m-3，導熱系數λb=130 W·m-1·K-1），熱源材料為銅(cp=385 J·kg-1·K-1，ρ=8 960 kg·m-3，λs=400 W·m-1·K-1).T 形通道中冷卻介質為空氣，通道內流體的流動為可壓縮穩態湍流流動（Re=2 889 ～8 668），通道外壁面為絕熱邊界條件，通道、熱源與空氣的接觸面為無滑移邊界條件，射流入口速度Uj垂直于入口端面，該處環境的空氣溫度設為293.15 K，通道兩出口端面為壓力邊界條件.

空氣流動的連續性方程、動量方程、能量方程、湍動能方程、湍流耗散率方程和湍流黏度方程分別為[21]

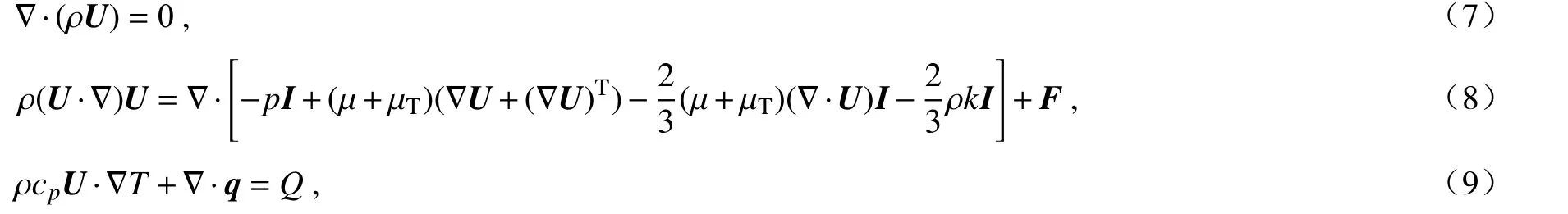
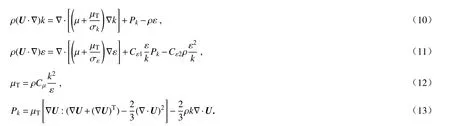
式(7) ～(13)中，I為單位矩陣，F為體積力，μ為分子黏性系數，μT為湍流黏性系數，k和ε 分別為湍動能和湍流耗散率，Q為包含黏性耗散和壓力功在內的熱源項，Pk為湍動能的生成項.Cε1，Cε2，Cμ，σk，σε均為經驗常數，取值分別為[25]：Cε1=1.44，Cε2=1.92，Cμ=0.09，σk=1，σε=1.3.

常物性固體基底穩態導熱的能量方程為

常物性熱源穩態導熱的能量方程為

圖1所示散熱系統的熵產率為

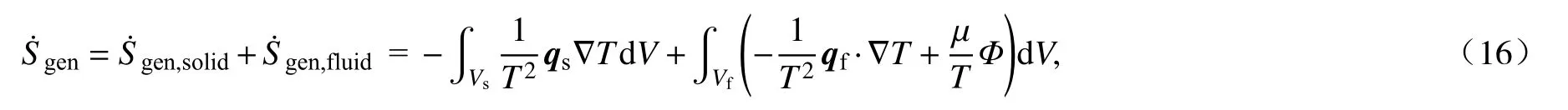
式中，等號右側括號中第一部分為固體熵產率，第二部分為流體部分產生的熵產率.Ф為單位體積黏性耗散函數，q為熱流密度矢量，單位W·m-2；μ為分子黏性系數，單位Pa·s.

綜上所述，圖1所示模型的構形設計問題可概括如下：

① 優化對象，射流通道內的方柱熱源；

② 優化目標，系統最高溫度和熵產率；

③ 優化變量，熱源間的長度比；

④ 約束條件，熱源縱截面面積和熱源高度一定；

⑤ 影響因素，熱源間距占通道長度的比值和射流速度.

1.3 數值求解方法

利用COMSOL Multiphysics 有限元數值計算軟件求解散熱模型的控制方程和邊界條件.采用標準k-ε 湍流模型，對固體和流體區域分別進行邊界層網格和自由三角形網格剖分，對網格獨立性進行了測試.在離散熱源的長度和高度都相等，熱源間距占通道總長度比值γ=0.2的情況下，利用物理場控制網格，單元大小按細化、較細化和超細化標準設置，對數值計算結果進行驗證，3 套網格的數量、對應的單元體內最高溫度及相對誤差如表1所示.考慮計算精度和效率，選擇單元數為69 132的較細化網格劃分策略計算網格.連續性、動量和能量方程的收斂標準均為1 × 10-6.

表1 網格獨立性檢驗Table 1 The grid independence test

為了進一步評估本文計算模型的準確性，建立文獻[22]的熱源模型，其中為熱源圓柱體的無量綱高度，b為肋片和熱源中心距與肋片半徑的比值，以無量綱最大溫差為評價指標進行對比，結果如表2所示.對于相同的和b，的最大相對誤差為0.85%，說明本文算法是可靠的.

表2 模型有效性驗證Table 2 Validation of the model

2 結果與討論

2.1 最高溫度最小化構形設計

圖3～5 給出了速度大小Uj分別為1 m/s，2 m/s 和3 m/s，熱源間距占比γ=0.2，0.3 和0.4 時，熱源長度比β與最高溫度Tmax的關系.

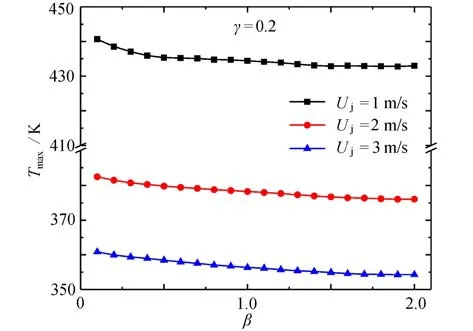
圖3 γ=0.2 時，Uj 對Tmax 與β 關系的影響Fig.3 Effects of Uj on the relationship of Tmax vs.β for γ=0.2

如圖3所示，當γ=0.2 時，Tmax均隨β的增大而減小，最后趨向于平穩.這表明熱源2（即射流入口下方的熱源）長度越小，兩側熱源長度越大，則熱源的最高溫度越小.但隨著β持續增大，Tmax減小的趨勢減緩并趨于穩定，此時提高β已難以改善系統散熱性能.當β給定時，隨著Uj的增大Tmax減小，即射流速度越大，系統散熱效果越明顯.

如圖4所示，當γ=0.3 時，Tmax均隨β的增大先減小后增大，即存在最優的βopt，使得Tmax取得最小值Tmax,min.當β＜βopt時，Tmax的遞減斜率較大，即β的大小對Tmax的影響較大；當β＞βopt時，Tmax的遞增斜率較小，即β大小對Tmax的影響較小.這主要是由于熱源2 距離射流入口較近，當其長度較大時，受射流垂直沖擊的散熱面較大，散熱效果較好，而兩側熱源距離射流入口較遠，因此其長度大小的變化對散熱效果的影響較弱.

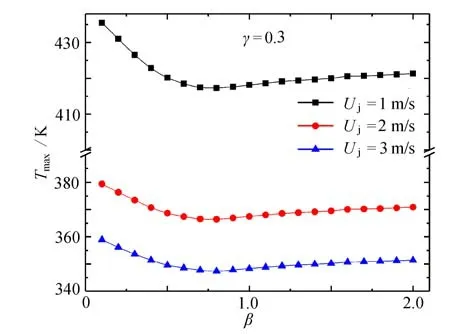
圖4 γ=0.3 時，Uj 對Tmax 與β 關系的影響Fig.4 Effects of Uj on the relationship of Tmax vs.β for γ=0.3

由圖5可知，當γ=0.4 時，Tmax均隨β的增大先減小后增大，且均存在最優的βopt，使得Tmax取得最小值Tmax,min.這表明實際應用中，隨著熱源間距的增大，設計人員可考慮將靠近射流入口的發熱器件的長度增大，兩側發熱器件長度減小，增大受射流沖擊面，降低系統溫度.

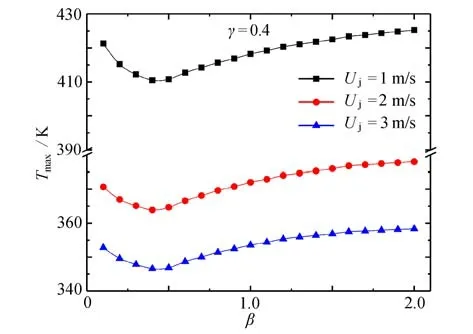
圖5 γ=0.4 時，Uj 對Tmax 與β 關系的影響Fig.5 Effects of Uj on the relationship of Tmax vs.β for γ=0.4

綜合對比圖3～5 可知，當Uj和β給定時，隨著γ的增大，Tmax減小.這主要是因為熱源間距增大時，射流流體能夠更加充分地沖擊導熱基座，使得導熱基座的散熱效果增強，間接地強化了熱能從高溫熱源向低溫導熱基座轉移的過程，從而提升了熱源的散熱效果.并且，隨著γ的增大，βopt減小.這表明，隨著熱源之間的間距增大，導熱基座受射流沖擊的表面積增大，其散熱效果增強.同時，熱源2 長度的增大也增加了與導熱基座的接觸面積和受射流沖擊的表面積，更有利于散熱.而兩側熱源由于距離射流入口較遠，所以其長度的變化對熱源散熱效果的影響較小.

表3給出了不同Uj和γ 與最優長度比βopt和Tmax,min之間的關系.

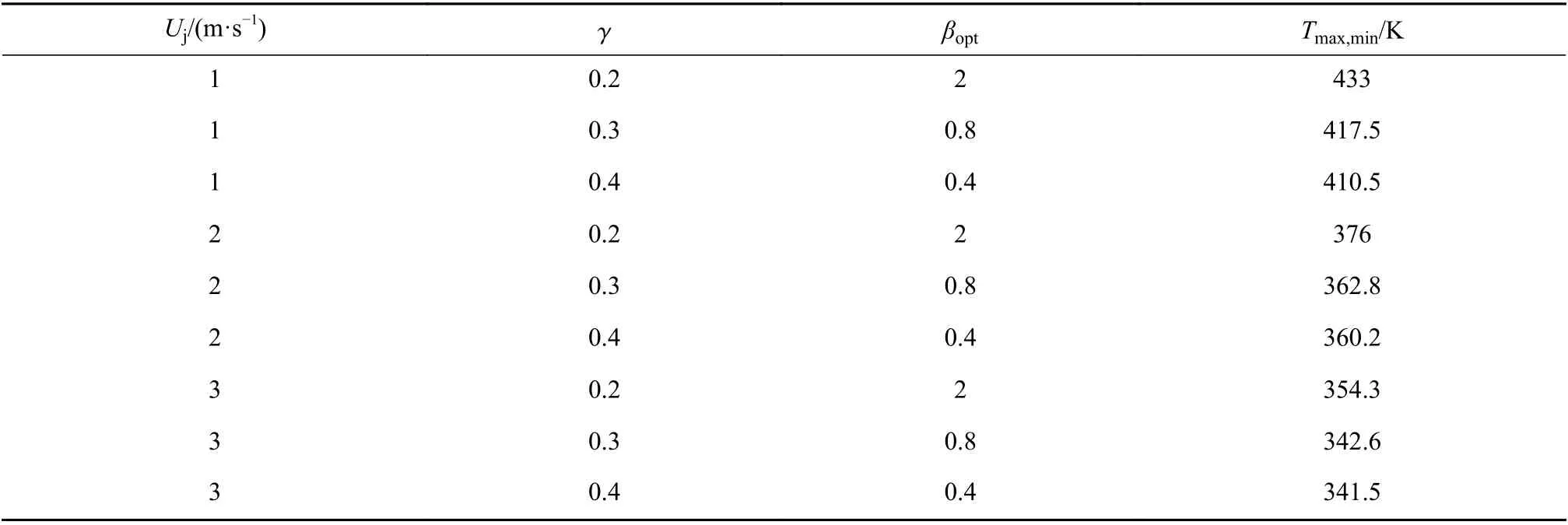
表3 不同Uj 時，Tmax,min 及對應的幾何參數Table 3 Tmax,min and its corresponding geometric parameters for different Uj values

圖6～8給出了3 種間距下，速度大小Uj為3 m/s 時，取最優長度比時的溫度等值線圖.從圖中可以看出，隨著γ的增大，等值線圖的高溫區域逐漸靠近通道底部和兩側出口處，射流入口附近始終是溫度最低區域.γ=0.2 時，高溫區域的面積比γ=0.3 和0.4 時的高溫區域的面積要大.而γ=0.3 時，導熱基座上的高溫點比γ=0.4 時的高溫點分布更加均勻，且均位于各離散熱源的兩側.

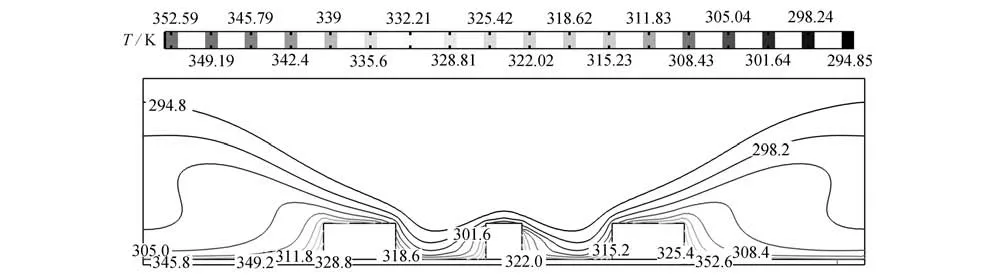
圖6 γ=0.2,β=2,Uj=3 m/s 時，溫度的等值線圖Fig.6 The temperature contour map for γ=0.2,β=2,Uj=3 m/s

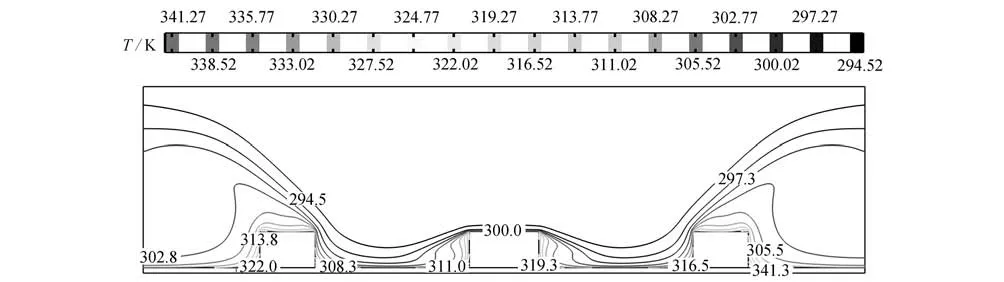
圖7 γ=0.3,β=0.8,Uj=3 m/s 時，溫度的等值線圖Fig.7 The temperature contour map for γ=0.3,β=0.8,Uj=3 m/s

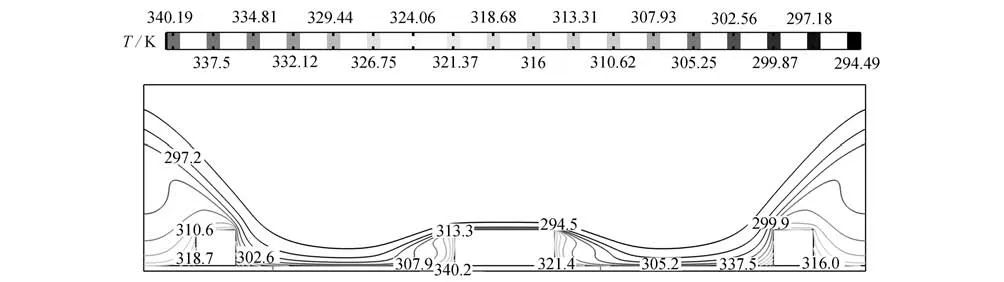
圖8 γ=0.4,β=0.4,Uj=3 m/s 時，溫度的等值線圖Fig.8 The temperature contour map for γ=0.4,β=0.4,Uj=3 m/s

2.2 熵產率最小化構形設計

圖9～11 給出了速度大小Uj分別為1 m/s，2 m/s 和3 m/s，熱源間距占比γ=0.2，0.3 和0.4 時，熱源長度比β與系統熵產率的關系.

注為了解釋圖中的顏色，讀者可以參考本文的電子網頁版本，后同.

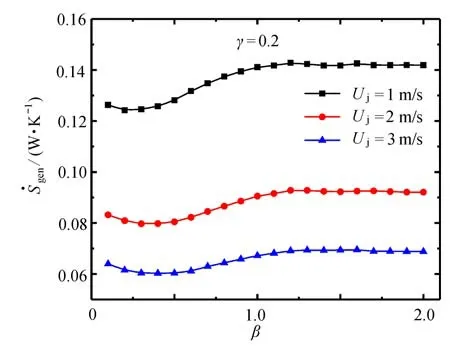
圖9 γ=0.2 時，Uj 對 與β 關系的影響Fig.9 Effects of Uj on the relationship of vs.β for γ=0.2

由圖10可知，當γ=0.3 時，隨著β的增大先減小后增大，存在最優長度比βopt使得達到最小值.當β＜βopt時，的下降斜率較大.當β＞βopt時，的上升斜率較小.這說明，當熱源2 長度大于兩側熱源長度時，β對的影響較大，而當熱源2 長度小于兩側熱源長度時，β的增大對的影響較小.這主要是因為β的減小增加了兩邊熱源與射流入口的距離，使得射流沖擊兩邊熱源的流動減弱，使一部分流體動能不可逆地耗散為熱，增加了系統熵產率.

圖10 γ=0.3 時，Uj 對 與β 關系的影響Fig.10 Effects of Uj on the relationship of vs.β for γ=0.3

由圖11可知，當γ=0.4 時，隨著β的增大先減小后增大，存在最優長度比βopt使得達到最小值.不同的是，當β大于或小于βopt時，單調增減的斜率相近.這表明，當熱源間的間距增大后，熱源間流場的流動更充分，使得熱源之間的長度比對流體流動的影響趨于相同.

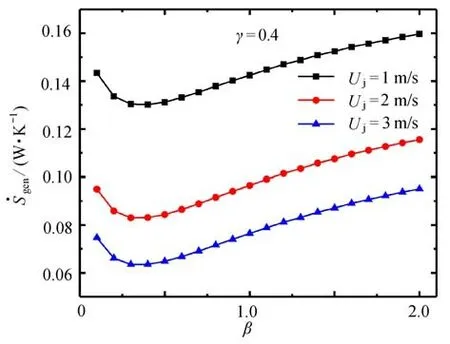
圖11 γ=0.4 時，Uj 對 與β 關系的影響Fig.11 EffectsofUjonthe relationship of vs.β for γ=0.4

綜合圖9～11 可知，當Uj和β給定時，隨著γ的增大，βopt先增大后減小.這主要是因為當熱源間距增大時，兩側熱源距離射流入口較遠，受射流冷卻流體的影響減小，所以其長度對對流傳熱效果的影響較小，而熱源2 長度增大后其影響增大，導致βopt減小.當熱源間距減小時，導熱基座受射流沖擊不充分，且βopt較小時，熱源2 上表面的增大阻礙了流體向兩邊出口的流動，流體在熱源上表面形成反射氣流，增強了渦旋，使流體旋轉動能轉變為熱能.

表4給出了不同Uj和γ 與最優長度比βopt和之間的關系.

表4 不同Uj 時，及對應的幾何參數Table 4 and its corresponding geometric parameters for different Uj values

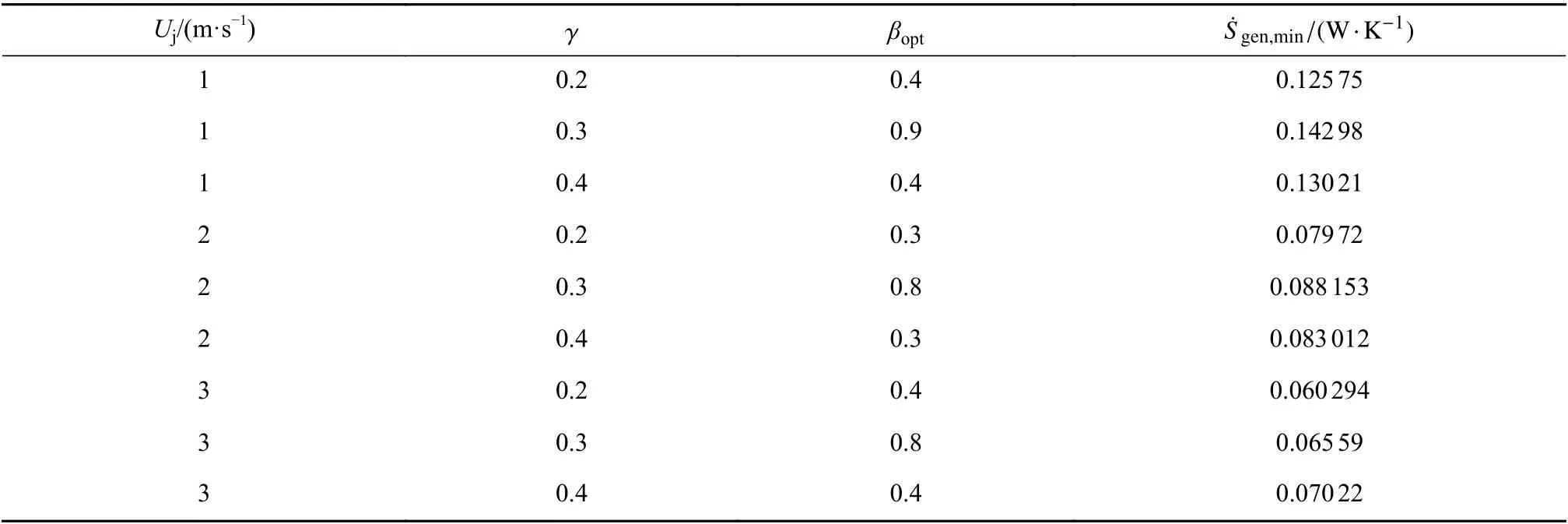
表4 不同Uj 時，及對應的幾何參數Table 4 and its corresponding geometric parameters for different Uj values

Uj/(m·s-1) γ βopt ˙Sgen,min/(W·K-1)1 0.2 0.4 0.125 75 1 0.3 0.9 0.142 98 1 0.4 0.4 0.130 21 2 0.2 0.3 0.079 72 2 0.3 0.8 0.088 153 2 0.4 0.3 0.083 012 3 0.2 0.4 0.060 294 3 0.3 0.8 0.065 59 3 0.4 0.4 0.070 22

圖12～14給出了三種間距下，速度大小Uj分別為1 m/s，2 m/s 和3 m/s 時，最優長度比的通道縱截面的速度分布圖.隨著γ的增大，射流與導熱基座的接觸面積不斷增大，這使得通道內流體流動克服沿程摩擦力所產生的能量損失不斷增大.同時，熱源的存在，使得流體的流動在熱源處、熱源上方和熱源之間存在明顯的局部繞流、流動阻滯和渦旋，其中流動阻滯增大了流動的耗散，渦旋強化了流體與熱源之間的對流傳熱.

圖12 γ=0.2,β=2,Uj=3 m/s 時，通道縱截面的速度分布圖Fig.12 The velocity profile of the channel longitudinal section for γ=0.2,β=2,Uj=3 m/s

圖13 γ=0.3,β=0.8,Uj=3 m/s 時，通道縱截面的速度分布云圖Fig.13 The velocity profile of the channel longitudinal section for γ=0.3,β=0.8,Uj=3 m/s

圖14 γ=0.4,β=0.4,Uj=3 m/s 時，通道縱截面的速度分布云圖Fig.14 The velocity profile of the channel longitudinal section for γ=0.4,β=0.4,Uj=3 m/s

3 結 論

本文建立了二維T 形通道內的方柱離散熱源散熱模型，研究了在離散熱源縱剖面面積和熱源高度一定的約束條件下，熱源之間的長度比、間距和入口射流速度對系統最高溫度和系統熵產率的影響.主要結論如下：

1) 當離散熱源縱剖面面積和熱源高度一定時，分別存在不同的最優熱源長度比使得系統最高溫度最小和系統熵產率最小.

2) 當熱源之間長度比和入口速度一定時，熱源間距越大，系統最高溫度最小值越小，而系統熵產率最小值越大.

3) 當熱源之間的長度比和間距一定時，入口射流速度越大，系統最高溫度和系統熵產率越小.

4) 當熱源間距較小時，增大熱源之間的長度比有利于降低系統的最高溫度；當熱源間距較大時，減小熱源之間的長度比有利于降低系統的最高溫度.并且，在不同間距條件下，最高溫度最小值所對應的最優熱源長度比也不同.