新課標下函數的教學策略研究
蒲志勇
(廣東省中山市實驗中學,廣東 中山 528404)
一、熟讀教材,理解編者目的
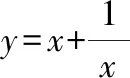
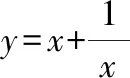
二、善于思考,創新教學模式
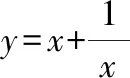
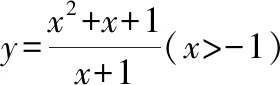
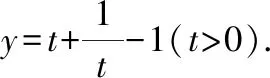
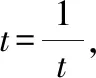
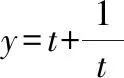
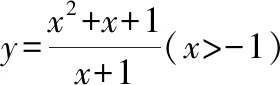
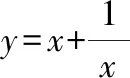
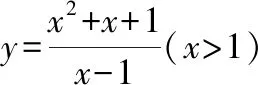
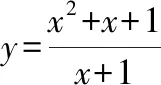
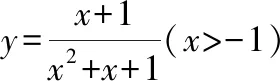
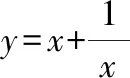
三、鞏固精煉,有效綜合練習
學生不能只學習書本的知識概念,必須要通過練習去加強自身對知識的理解與掌握練習是一個非常重要的環節如果學生只是學會了書本知識而不加以練習,那么對書本知識的理解不能長久記憶,是膚淺的、片面的所以,教師在知識學習后布置一定量的習題練習是非常必要的,而且布置什么樣的練習也是很有學問的
1要建造一個容積為1200 m,深為6 m的長方體無蓋蓄水池,池壁的造價為95元m,池底的造價為135元m,如何設計水池的長與寬,才能使水池的總造價控制在7萬元以內(精確到01 m)?
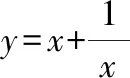
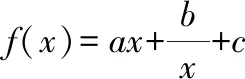
(1)求,,的值
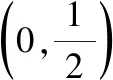
該題相對前一題適用性弱一些,理論性較強,體現出數學的理論研究特點該題既是對函數基本知識的練習(待定系數法求參數和奇偶性的應用),也是對數學嚴密邏輯推理的訓練,比如第二問的證明,可以讓學生進一步學會結合專門的數學術語用定義去證明問題,有利于提升學生思維的嚴密性和邏輯推理能力
四、知識提升,拓寬學生視野
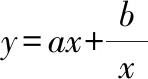
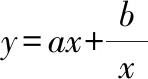
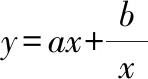
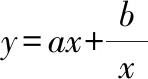
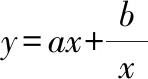
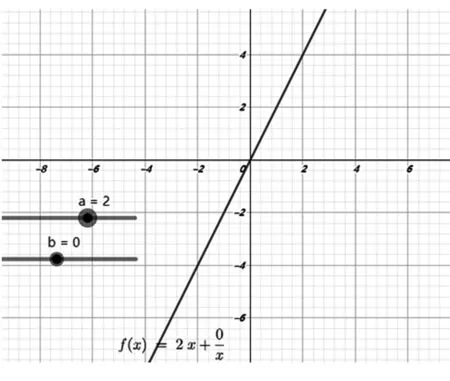
圖1
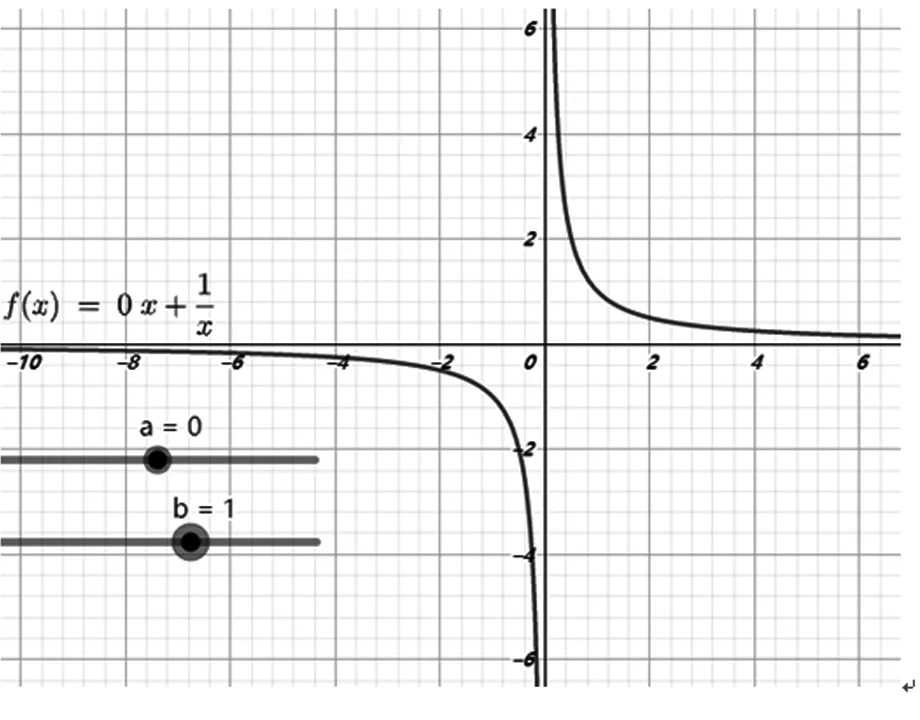
圖2
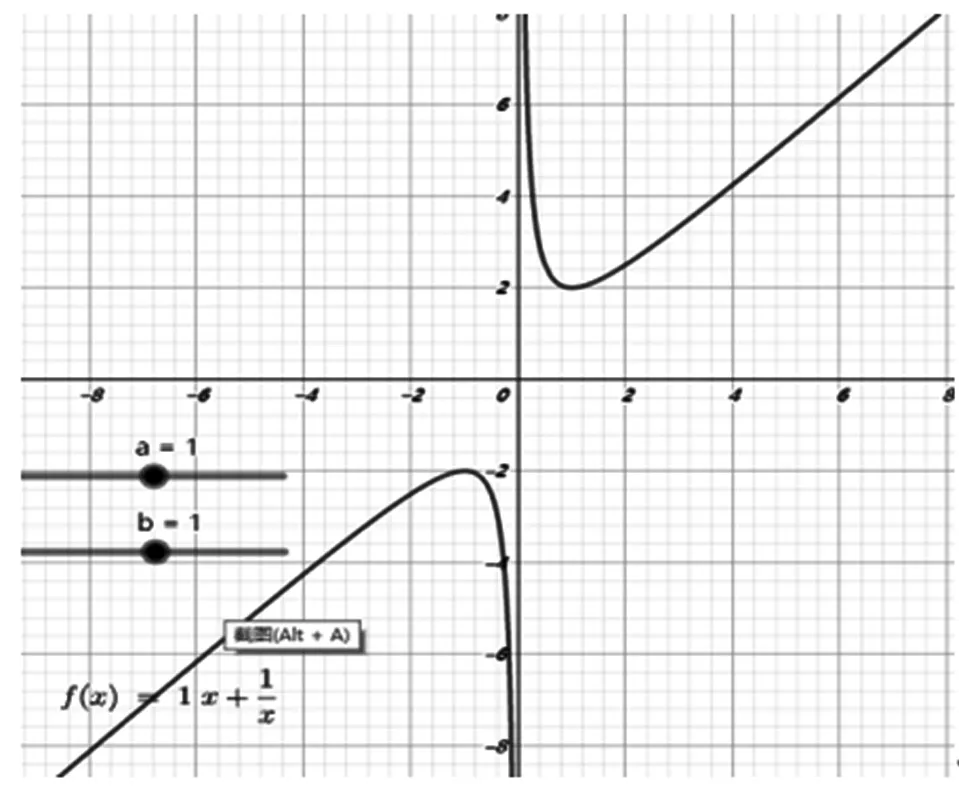
圖3
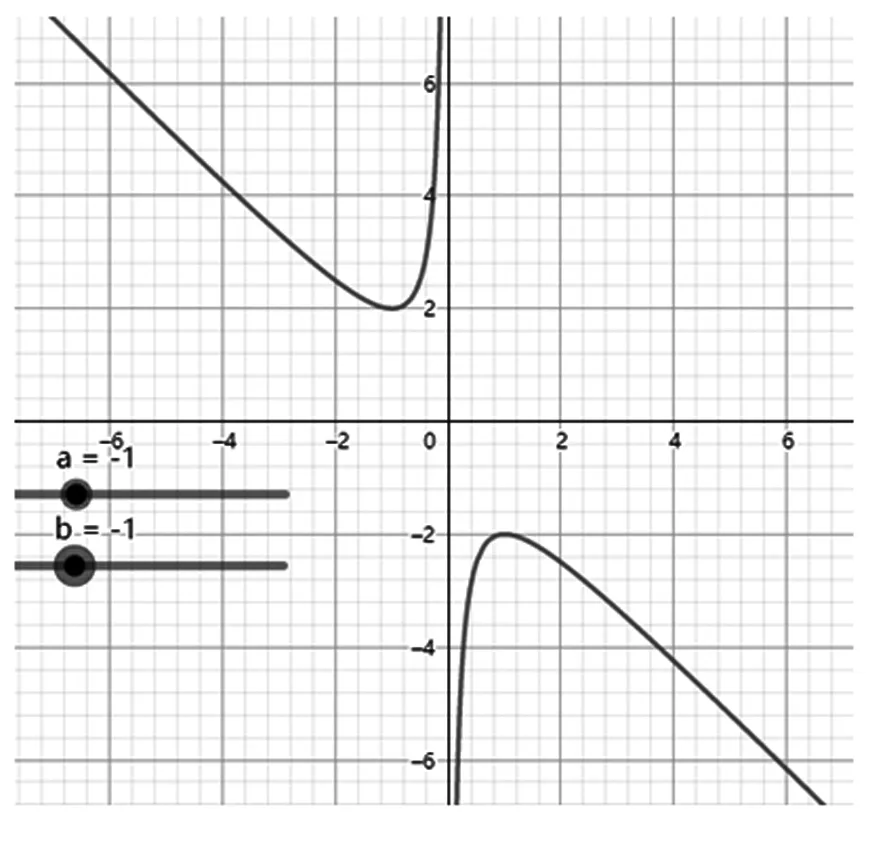
圖4
首先,由圖像可得到函數定義域、值域、奇偶性、單調性、對稱性、最值等其次,改變參數,的值,觀察函數的圖像形狀和變化情況,得出相應性質最后,觀察函數圖像,注意函數分別在哪些位置取到最小值和最大值,特別是借助基本不等式確定取到最值時相應的值
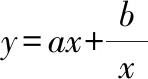
1定義域:{|∈,≠0};
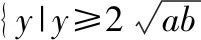
3圖3、圖4呈“對勾”形狀,是中心對稱圖形(關于原點對稱),是奇函數,可進一步用(-)=-()檢驗;
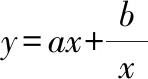
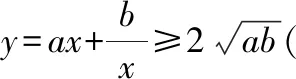
當<0時,其性質可仿照>0得到
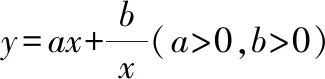
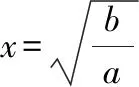
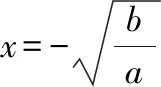
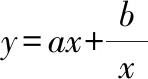
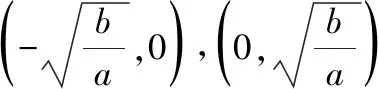
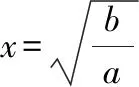
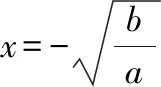
互動交流:當,同號時,雖然我們也可以通過函數的解析式判斷它的定義域、奇偶性,但是從圖像上可以更加直觀地發現這些性質,特別是最值與單調區間由圖像更加容易得到,當然要借助基本不等式來求得準確的最值點和最值,這也進一步體現出數形結合的魅力——數缺形時少直觀,形缺數時難入微!
以上的研究都是在,同號的情況下進行的,教師可結合學生實際,引導其繼續探索>0,<0或<0,>0的情況,讓學生感受數形結合的魅力我們借助數學軟件畫圖進行研究,可以讓問題變得直觀、簡單如圖5、圖6
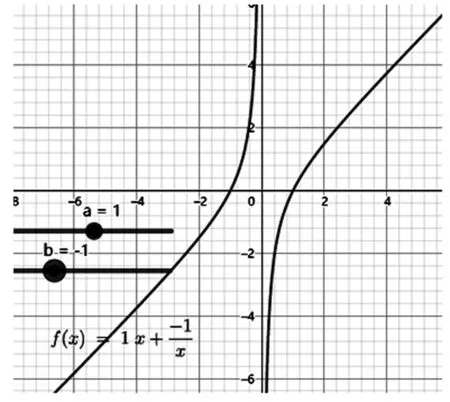
圖5
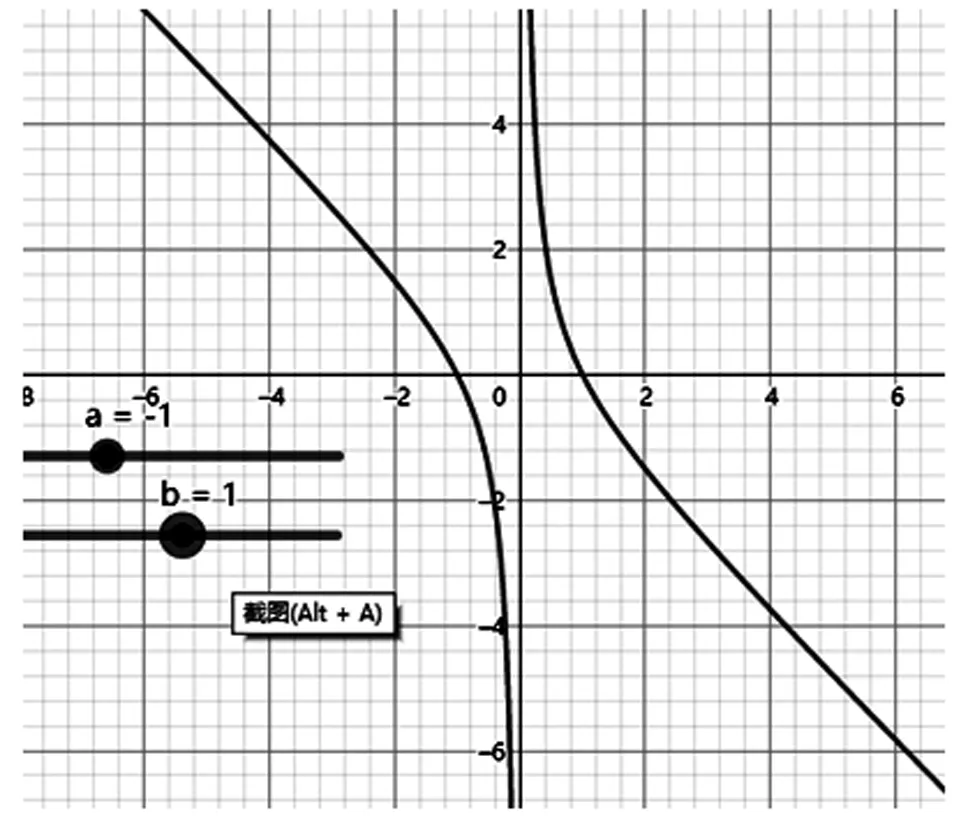
圖6
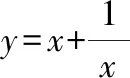
本研究為學生進一步學習提供了必要的數學準備,且使得不同層次的學生在數學上得到不同的發展,為學生提供多層次、多種類的選擇,促進學生個性化的發展教師應倡導積極主動、勇于探索的學習方式,讓學生動手實踐、自主探索、合作交流,使學習過程成為“再創作”的過程學生體驗發現知識和創新解法的歷程,有利于發展自身的創新意識,也有利于提高自身的數學思維能力,以及直觀感知、觀察發現、歸納類比、抽象概況、反思與體系建構等思維過程教師應發展學生的數學應用意識,注重數學活動過程,注重數學思想方法教學,讓學生體會其在后續學習中的作用此外信息技術的應用使得數學問題可以用圖形的和符號的方式進行表達、解決,并在這些表示方式間進行轉換,形成更多的解決問題的方法,使學生逐漸成為更加主動的學習者,形成更高級的概念與能力

