可微函數及其平方積分的估計

李容星

(湖北師范大學文理學院，湖北 黃石 435109)

一、引 言

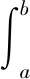
二、柯西-施瓦茨定理

我們先引入柯西-施瓦茨定理：

設函數()和()都在[,]上可積，則

柯西-施瓦茨定理有如下簡單的推論：

設函數()在[,]上可積，則

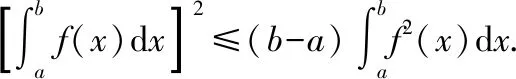
在柯西-施瓦茨定理中取()=1即可得證

設函數(),()在上連續可微，則

由引理1可得

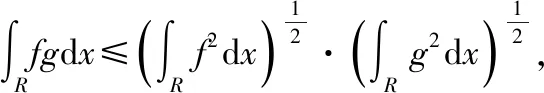
于是

即推論2得證

設函數(,)在上連續可微，則

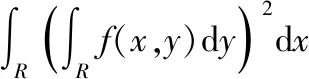
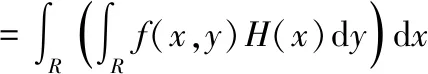
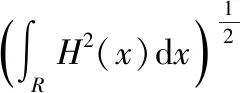
即定理1得證

三、可微函數平方積分的估計

我們首先對函數本身進行估計：

由牛頓-萊布尼茨公式有

由引理2有

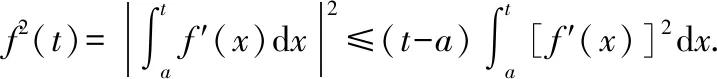
(1)

同理有

從而

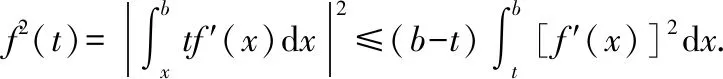
(2)

由(1)(2)式有

(-)()=(-)()+(-)()

(3)

即

即定理2得證

從定理2的證明過程中我們可以對函數的積分進行估計：

設函數()在[,]上連續可微，且()=()=0，則

由定理1證明過程中的(3)式，對?∈[,]有

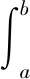
兩邊對積分有

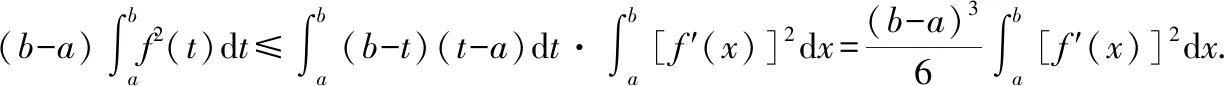
從而

即定理3得證

繼續研究定理3的證明過程我們可以得到如下結論：

設函數()在[,]上連續可微，且()=()=0，則

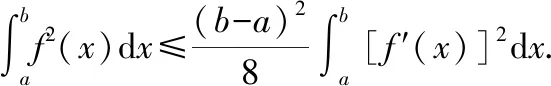
由定理2證明過程中的(1)(2)式，對?∈[,]有

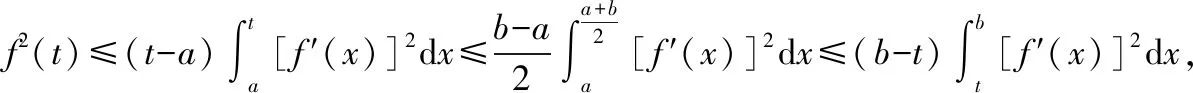
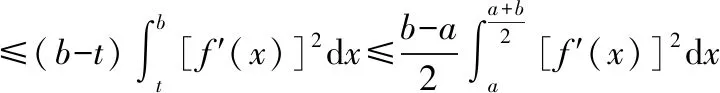
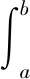
累次積分變換積分次序可得

(4)

累次積分變換積分次序可得

(5)

從而由(4)(5)式有

即定理4得證

四、可微函數其他積分的估計

利用上述的結論可以對函數及其導數的乘積進行估計：

設函數()在[,]上連續可微，且()=()=0，則

證 由引理1和定理4可得

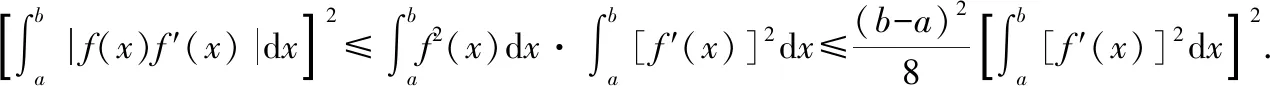
從而

即定理5得證

利用定積分與原函數的關系也可以對定理2的結論進行改進：

設函數()在[,]上連續可微，且()=()=0，則

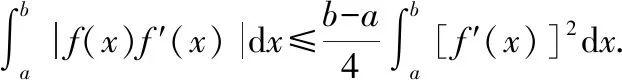
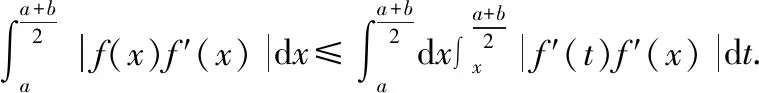
兩式相加，并利用推論1可得

同理可得

故而

即定理6得證

五、在高等數學中的應用

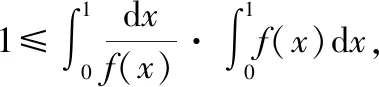
因此該題得證

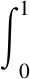
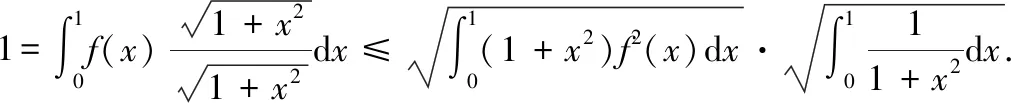
六、結 語

利用函數的性質以及相關的定理與公式對函數及其變式的積分進行估計是數學分析中一個非常重要的工作在第一部分，本文先對函數本身進行估計，然后利用柯西-施瓦茨定理對函數的平方進行估計，接著利用重積分可以交換積分順序的特性來改進結果在第二部分，本文利用第一部分的結果，對函數及其導數的乘積進行估計該思想的本質是利用柯西-施瓦茨定理結合函數本身導數的性質對函數進行估計，只要掌握好該思想，就能夠簡化高等數學中相關問題的推導，對函數的積分進行更好的估計