成都市臭氧生成對氣象因素的敏感性分析

侯夢琪，明鎮洋，付 虹，李 迪，劉岳軍

（西南交通大學地球科學與環境工程學院，成都 611756）

氮氧化物（NOx）是臭氧（O3）生成的根本，揮發性有機物（VOCs）是O3濃度升高的增長劑，氣象因子是O3生成的基本條件，量化氣象因子對O3生成的影響是研究O3生成機理的重要內容。KOVACANDRIC 等[1]采用傅里葉分析、主成分分析（PCA）以及多元線性回歸分析等方法研究了克羅地亞東部氣象變化與O3濃度的關系，結果表明，溫度、太陽輻射時間、能見度和壓力有利于O3的形成，相對濕度和云量降低了O3濃度。DAWSON等[2]基于CMAx模型，模擬分析了O3濃度對美國東部地區氣象因子的敏感性，研究結果表明，溫度對O3影響最大，溫度每升高1 K，O3濃度升高0.73 μg/m3；絕對濕度對該指標的影響較小但顯著；風速、混合層高度、云液態水含量和光學厚度對該指標的影響極小；對于超標日濃度而言，溫度的影響最大，其次為風速和混合層高度。楊成江等[3]對吉林省O3污染與氣象要素關系的研究表明，吉林省O3平均濃度隨氣壓升高先增后減，與氣溫指標呈正相關。張磊[4]分析了氣象要素對遼中地區O3的影響，發現太陽輻射和紫外輻射是影響遼中地區O3的主要氣象因素。王玫等[5]利用相關系數分析了2014—2017年京津冀地區13 座城市O3與氣象因子的相關性，指出冬季影響京津冀地區O3濃度變化的主要因素是相對濕度與風速，其他季節氣溫是主要因素。胡成媛等[6]利用2015—2016年四川盆地18個城市的國控站點監測數據及氣象臺站數據，采用廣義加性模型（GAM）對影響四川盆地O3污染的主要氣象因子進行識別，結果表明，臭氧與各氣象因子均呈非線性關系，日照時數、相對濕度和氣溫是影響四川盆地O3濃度的主要氣象因子。李英杰等[7]對成都中心城區O3濃度與各個氣象要素進行研究，結果表明，成都中心城區近地面產生高濃度O3的主要氣象因素為高溫度、較低濕度、高邊界層、無降水以及偏南風。由此可見，不同地區氣象要素對O3污染的影響存在差異。

為了更加準確地揭示氣象因子對成都市O3的影響程度，有必要建立可靠的臭氧預測模型，針對O3對各氣象因子的敏感性，確定影響成都市O3的主要氣象因子序列。本文利用2015—2019年成都市西南交通大學站污染物濃度監測數據、同期氣象監測數據以及探空資料，構建BP 神經網絡臭氧預測模型，之后采用全局敏感性分析方法，分別研究成都市O3濃度對上述氣象因子的敏感度，以此確定影響成都市O3濃度的主要氣象因子。

1 數據來源與方法

1.1 數據來源

本文所使用的O3-1 h 濃度數據及氣象監測數據來源于四川省環境空氣質量綜合監測站，該站點位于成都市金牛區西南交通大學九里校區土木工程學院樓頂。氣象監測數據內容包括太陽輻射（W/m2）、相對濕度（%）、溫度（℃）、氣壓（hPa）、風向（°）和風速（m/s）。混合層高度（m）數據利用探空數據計算得到，其中探空資料來源于成都溫江探空站（站點編號56187）。時間為2016年1月1日至2019年12月31日。本研究已參照《環境空氣質量標準》（GB 3095—2012）的規定，對數據進行篩選和剔除，數據有效性滿足要求。

1.2 臭氧濃度的BP 神經網絡模型

1.2.1 模型建立方法

本文基于2016—2018年氣象數據及O3濃度監測數據，采用后向傳播（BP）神經網絡模型構建臭氧濃度預測模型。網絡初始化是構建BP 神經網絡模型的先決條件，可直接影響模型的準確性。網絡輸入層、輸出層和隱含層節點數、各層之間的連接權重值、學習率以及最大迭代次數等參數均需要在初始化過程中設置和選定。網絡輸入層節點數n由輸入參數的個數決定，輸出層節點數m則取決于輸出參數的個數。由于本文擬構建利用溫度、相對濕度、大氣壓力、太陽輻射強度、混合層高度、風速等氣象因子預測臭氧濃度的神經網絡模型，因此本文將輸入層節點數n設置為6。輸出數據為臭氧濃度，即本研究中輸出層節點數m設置為1。

本研究首先參照經驗公式計算隱含層節點數范圍，再通過多次調試對比，得出最合適的隱含層節點數。節點數范圍參考式（1）確定。

式中：l為隱含層節點數；a為（0，10）區間內的常數[8]。

由計算可知，隱含層節點數應在一定范圍內選取[3]，經模型多次調試比較后，最終確定將隱含層節點數設置為4。

迭代次數影響隱含層節點的調整和權重值的更新。經多次測試比較，最終采用的學習率為0.001，最大迭代次數為20 000 次。選用ReLU 函數作為BP神經網絡模型的激活函數f(z)，并以此對數據進行非線性處理。選用均方差函數作為BP 神經網絡模型的損失函數，以此表征模型輸出與期望輸出的誤差大小。

1.2.2 模型評估方法

利用標準化平均偏差（NMB）、標準化平均誤差（NME）以及相關系數（R）等指標來驗證神經網絡模型的可靠性。NMB和NME表示模型輸出值和觀測值的偏離程度，其絕對值越小表明模型輸出值越接近觀測值；R用于表征模型輸出值和觀測值的接近程度，其值越接近1，表明模型輸出值與觀測值越接近。

1.3 敏感性分析方法

敏感性分析是研究模型各個輸入參數對模型輸出的影響程度[9-10]，通過對模型進行敏感性分析，對模型輸入參數進行敏感性排序，可以確定影響模型輸出的關鍵參數。目前，敏感性分析在生物學模型和水文水質模型等方面的應用已較為廣泛[11-13]。敏感性分析主要分為局部敏感性分析和全局敏感性分析兩類，其中，局部敏感性分析忽略了各輸入參數的相互作用，不適用于非線性模型，且無法計算高階敏感性。全局敏感性分析可以研究多個輸入參數同時變化對模型輸出的影響，克服了局部敏感性分析的缺點。常見的全局敏感性分析方法包括回歸分析法、Morris 篩選法、Sobol 法、傅里葉振幅敏感性分析法（FAST）和區域敏感性分析法（RSA）等。

Sobol 法是一種基于方差的分析方法，以輸入參數對模型輸出方差的貢獻比例衡量參數敏感性[14]，適用于非線性模型，計算結果穩定可靠，目前已在環境領域的非線性模型中有較多應用[15-17]。

Sobol 法的核心思想是將模型輸出的總方差分解為每個輸入參數的方差和多個輸入參數間相互作用的方差，然后通過輸入參數對輸出方差的貢獻比例進行敏感性分級[18]。Sobol 法模型函數可表示為

式中，Y為模型輸出值；X={X1，X2，…，Xn}，其為模型的輸入參數數據集。

將函數f(X)的總方差D(Y)表示為每個輸入參數的方差和多個輸入參數間相互作用的方差之和，即

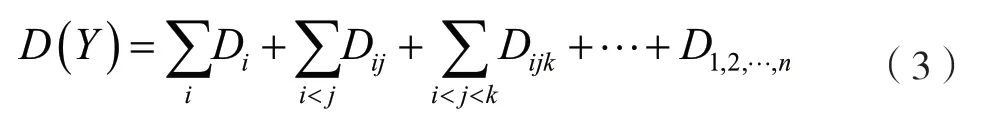
式中：Di為輸入參數Xi產生的方差；Dij為輸入參數Xi和Xj相互作用產生的方差；Dijk為參數Xi、Xj和Xk共同作用產生的方差；D1，2，…，n為參數模型X1、X2、…、Xn共同作用產生的方差。

根據對總方差D(Y)的貢獻比例，可計算得到各階Sobol 敏感性指數。

一階敏感性指數用公式可以表示為

二階敏感性指數用公式可以表示為

總敏感性指數用公式可以表示為

式中：Si用于表征輸入參數Xi單獨作用的敏感度；Sij為輸入參數Xi和Xj相互作用的敏感指數；STi為參數Xi的總敏感性指數；D～i表示除參數Xi外其他參數共同作用產生的方差。

2 結果與分析

2.1 模型的構建及模擬結果評價

利用2016—2018年西南交通大學站O3濃度數據和溫度、相對濕度、大氣壓力、太陽輻射強度、混合層高度、風速等氣象監測資料作為學習樣本數據集，應用Python3.7 軟件構建BP 神經網絡預測模型，訓練過程的誤差曲線如圖1所示，在第8 285 次訓練時，輸出誤差已收斂至0.5。選取2019年O3濃度監測數據和氣象數據作為驗證樣本數據集，運用構建的神經網絡模型，對2019年O3濃度進行預測，將預測值與觀測值進行分析對比，以此評估模型的可靠性。

圖1 BP 神經網絡訓練誤差曲線

將2019年4月、7月、10月、1月作為春夏秋冬代表月，對比臭氧日均濃度的預測值和監測值，如圖2所示。從圖2可以看出，O3濃度預測值和監測值的變化趨勢整體一致，兩者的NMB、NME及相關系數R如表1所示。

圖2 2019年四季臭氧日均濃度的預測值和監測值對比

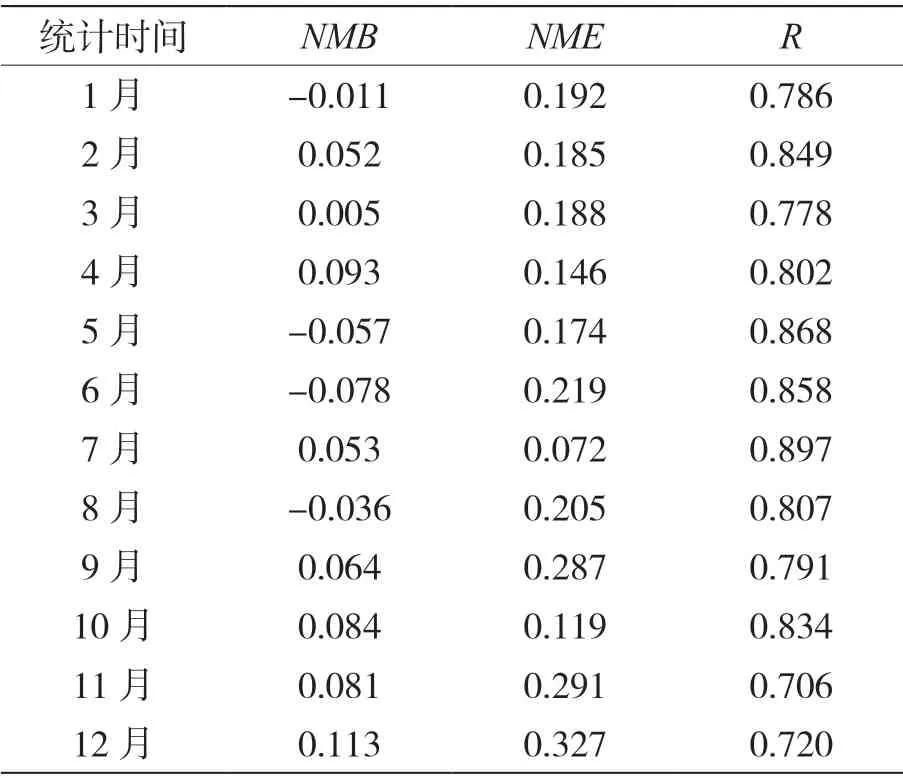
表1 BP 神經網絡模型模擬結果評價指標

由表1可知，BP 神經網絡模型輸出值與實際監測值吻合度較高，逐月相關系數均大于0.7，其中7月模型輸出值和實際監測值的相關性最高，相關系數R達0.897；NMB的絕對值均小于0.12，NME的值保持在0.072～0.327，這表明模型輸出值和實際監測值的偏離程度較小。因此，可利用該模型對O3濃度進行預測，進而用于后續全局敏感性分析。

2.2 O3 濃度對各氣象因子的敏感性分析

2.2.1 敏感性指數計算

由于Sobol 法的求解過程計算量較大，且存在高次積分，計算難度大，因此本研究采用基于蒙特卡洛的估計來模擬積分求解過程[19]，計算輸入參數的一階敏感性指數、二階敏感性指數以及總敏感性指數。本研究利用2016—2019年的污染物濃度和氣象監測數據分析O3濃度變化對各氣象因子的敏感性，其中輸入參數共計6 個，分別為溫度、相對濕度、大氣壓力、太陽輻射強度、風速以及混合層高度，輸出參數為O3濃度。下面分析具體的抽樣和計算過程。

首先，將溫度、相對濕度、大氣壓力、太陽輻射強度、風速以及混合層高度分別視作輸入變量X1、X2、X3、X4、X5、X6，采用Sobol 隨機序列采樣方法在各輸入參數變化范圍內隨機抽樣7 000 次，生成兩組樣本，將抽取的樣本分為矩陣A和矩陣B。

式中：N代表樣本點個數，為3 500 個。

其后，用矩陣A中的某列數據替換矩陣B中的對應列，生成新的矩陣Ci；將矩陣A中的某列數據替換為矩陣B中的對應列，生成新的矩陣C～i。矩陣Ci和C～i可以表示為

其次，將矩陣生成的每組輸入參數輸入BP 神經網絡模型進行計算，可得到對應每組輸入參數的模型響應輸出值，根據式（11）至式（14）計算模型響應的方差估計和各參數敏感性指標。

式中：表示模型總方差；表示輸入參數Xi的方差；表示除輸入參數Xi以外其他參數的方差；xr1表示第r行第1 列的參數，其他參數同理；表示輸入參數Xi和Xj的方差。

傅里葉變換后的一階敏感性指數為

傅里葉變換后的總敏感性指數為

采用上述計算方法得到傅里葉變換后兩個輸入參數相互作用的二階敏感性指數，即

式中：Si用于表征輸入參數Xj單獨作用的敏感度。

最后，通過比較各氣象因子的一階敏感性指數、二階敏感性指數以及總敏感性指數的大小，確定影響成都市O3污染的主要氣象因子序列。

2.2.2 一階敏感度和總敏感度

一階敏感性指數Si是指輸入參數Xi固定時模型輸出響應量總方差的平均減小量與總方差的比值，可用于表征輸入參數Xi單獨作用時對輸出方差不確定性的貢獻，即各氣象因子單獨作用對臭氧變化的影響，Si越大，說明該氣象因子Xi對臭氧濃度變化影響越大[20]。總敏感性指數STi表征了輸入參數Xi對輸出響應量的總影響程度，即STi除包括各氣象因子的單獨作用外，還包括各氣象因子相互作用對臭氧濃度產生的影響。若STi和Si均較小，則表明該氣象因子對臭氧濃度影響較小，且與其他氣象因子的相互作用效應也很小；若STi較大而Si較小，則表明該氣象因子對臭氧濃度影響較小，但其與其他氣象因子的相互作用效應較大。因此，在確定影響成都市O3污染的主要氣象因子序列時，既需要分析其一階敏感度，還需要考量其總敏感度。

本研究利用大氣溫度、相對濕度、大氣壓力、太陽輻射強度、風速以及混合層高度等氣象因子作為輸入參數，并將其按順序分別視作輸入變量X1、X2、X3、X4、X5、X6。為減小極端值對后續分析的影響，本研究以2016—2019年各氣象因子數據的第10 百分位值作為取值范圍的下限，以各氣象因子數據的第90 百分位值作為取值范圍的上限，統計結果如表2所示。采用Sobol 隨機序列采樣方法在各輸入參數變化范圍內隨機抽樣7 000 次，得到矩陣A和矩陣B。根據上述方法，可以計算各氣象因子的一階敏感性指數和總敏感性指數，結果如圖3所示。

表2 各輸入參數變化范圍

圖3直觀地對比了各氣象因子對臭氧的敏感度差異，柱狀圖分為上下兩部分。圖3中，下柱體代表一階敏感度；上柱體表示除一階敏感度以外的總敏感度部分，即參數的相互效應；下柱體加上柱體的和表示總敏感度。若某輸入參數的總敏感度超過閾值0.1，則定義該參數為敏感參數[21]。可以看出，不同氣象因子的一階敏感度和總敏感度差異較大。對一階敏感性指數進行對比，結果表明，各氣象因子對成都市臭氧濃度的影響大小排序為太陽輻射強度X4（0.220 3）＞大氣溫度X1（0.218 7）＞混合層高度X6（0.068 2）＞相對濕度X2（0.037 3），氣壓X3（0.005 8）和風速X5（0.000 8）的單獨作用對臭氧的影響極小。溫度、相對濕度、太陽輻射強度和混合層高度的總敏感性指數均大于0.1，其中，太陽輻射強度總敏感性指數最大（0.616 9），其后依次為溫度（0.560 7）、混合層高度（0.516 0）和相對濕度（0.260 0），氣壓（0.029 6）和風速（0.044 8）對臭氧的影響則較小。此外，每個氣象因子的一階敏感度占總敏感度的比例均較小，這表明各氣象因子的相互效應是影響臭氧濃度的重要因素。

圖3 各氣象因子對臭氧濃度的一階敏感度及總敏感度

2.2.3 二階敏感度

二階敏感性指數Sij可以反映輸入參數Xi和Xj的交互效應對輸出響應量的影響，其在本研究中用于表征兩個氣象因子相互作用對臭氧濃度的影響。Sobol敏感性分析中，將二階敏感性指數按大小劃分為不同區間，分別為很敏感、敏感和不敏感[22]，如表3所示。

表3 各氣象因子對臭氧濃度的二階敏感度

表4統計了各氣象因子的二階敏感性指數。可以看出，臭氧濃度對溫度、太陽輻射強度和混合層高度的相互作用都敏感（Sij≥0.01），其對溫度和太陽輻射強度的相互作用最為敏感（Sij=0.020 9）；其次為溫度和混合層高度的相互作用（0.015 5）；太陽輻射強度和混合層高度的相互作用排名第三（0.012 4）；臭氧濃度對其他氣象因子相互作用的敏感度極小，可視作不敏感。

表4 各氣象因子對臭氧濃度的二階敏感度

3 結論

一階敏感性指數分析結果表明，成都市各個氣象因子對臭氧濃度的敏感性排序為太陽輻射強度（0.220 3）＞溫度（0.218 7）＞混合層高度（0.068 2）＞相對濕度（0.037 3），氣壓（0.005 8）和風速（0.000 8）的單獨作用對臭氧的影響極小。二階敏感性指數分析結果表明，臭氧濃度對溫度、太陽輻射強度和混合層高度的相互作用較為敏感，其中臭氧對溫度和太陽輻射的相互作用最敏感，其次為溫度和混合層高度的相互作用，太陽輻射和混合層高度的相互作用排名第三，其他氣象因子的相互作用對臭氧濃度的敏感性極小。總敏感性指數分析結果表明，成都市溫度、相對濕度、太陽輻射強度和混合層高度的總敏感性指數均大于0.1，氣壓、風速的總敏感性指數均小于0.1，其中太陽輻射強度總敏感性指數最大（0.616 9），其后依次為溫度（0.560 7）、混合層高度（0.516 0）和相對濕度（0.260 0），氣壓（0.029 6）和風速（0.044 8）的總敏感性指數則極小，即主要影響成都市臭氧濃度變化的4 種氣象因子分別為太陽輻射強度、溫度、混合層高度和相對濕度。