對(duì)新教材“充分條件與必要條件”的思考與重構(gòu)

杜 瑛

(無錫市青山高級(jí)中學(xué)，江蘇無錫，214000)

在“立德樹人，提升素養(yǎng)”的理念下，《普通高中數(shù)學(xué)教科書(人教A版)》(以下簡稱“新教材”)對(duì)高中數(shù)學(xué)課程結(jié)構(gòu)進(jìn)行了重組與優(yōu)化，突出了數(shù)學(xué)教學(xué)的主線，凸顯了數(shù)學(xué)的內(nèi)在邏輯和思想方法.新教材在必修1中最大的結(jié)構(gòu)變化是將集合、常用邏輯用語、相等關(guān)系和不等關(guān)系、函數(shù)觀點(diǎn)看一元二次方程和一元二次不等式四部分內(nèi)容作為預(yù)備知識(shí)，放在其他教學(xué)模塊之前，旨在先教會(huì)學(xué)生使用基本的數(shù)學(xué)邏輯語言工具、明確最基本的數(shù)量關(guān)系、理解最基本的數(shù)學(xué)思想方法，幫助學(xué)生更順利地完成初高中銜接，為之后的學(xué)習(xí)做好鋪墊.

充分條件、必要條件和充要條件是三個(gè)常用的邏輯用語，是研究數(shù)學(xué)問題時(shí)經(jīng)常遇到的基本邏輯關(guān)系，是數(shù)學(xué)判定定理、性質(zhì)定理和定義的邏輯本質(zhì)，是表達(dá)數(shù)學(xué)對(duì)象的基本邏輯語言和論證數(shù)學(xué)結(jié)論的基本邏輯思維方向.

1 內(nèi)容簡析

1.1 課標(biāo)要求

本課是普通高中數(shù)學(xué)教科書人教A版第一冊(cè)第一章第二單元“常用邏輯用語”第一、二課的內(nèi)容.

本單元內(nèi)容包括：充分條件、必要條件、充要條件，全稱量詞與存在量詞、全稱量詞命題與存在量詞命題的否定.

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017版)》對(duì)兩課內(nèi)容的教學(xué)要求是：通過對(duì)典型數(shù)學(xué)命題的梳理，理解充分條件、必要條件和充要條件的意義，理解判定定理與充分條件、性質(zhì)定理與必要條件和定義與充要條件的關(guān)系.幫助學(xué)生使用常用邏輯用語表達(dá)數(shù)學(xué)對(duì)象、進(jìn)行數(shù)學(xué)推理，提高交流的嚴(yán)謹(jǐn)性與準(zhǔn)確性.

1.2 教材內(nèi)容

1.2.1 知識(shí)結(jié)構(gòu)

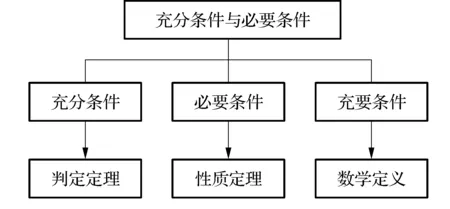
1.2.2 教材解讀

教材中，兩節(jié)課均以命題的真假為載體，第一課通過判斷命題真假總結(jié)出充分條件和必要條件的定義.例1和思考1加深對(duì)充分條件判斷方法的理解、探究判定定理與充分條件的關(guān)系；例2和思考2加深對(duì)必要條件判斷方法的理解、探究性質(zhì)定理與必要條件的關(guān)系.這樣安排一是考慮到教學(xué)內(nèi)容比較抽象，分別探究可以降低難度；二是通過兩個(gè)思考問題培養(yǎng)學(xué)生的論證能力，為第二課的學(xué)習(xí)做好鋪墊.

第二課“思考”中給出四個(gè)命題，既能總結(jié)出充要條件的概念，又給發(fā)現(xiàn)充分不必要條件和必要不充分條件埋下伏筆.通過例3、例4和探究問題的解決，提升學(xué)生邏輯推理素養(yǎng)，培養(yǎng)辯證求實(shí)的科學(xué)精神.

2 教學(xué)困惑

“充分條件與必要條件”原為舊教材選修2-1第一章第一單元內(nèi)容，安排為2課時(shí)，教學(xué)對(duì)象為高二年級(jí)學(xué)生.現(xiàn)被調(diào)整為新教材必修第一冊(cè)第一章第二單元內(nèi)容，安排為2課時(shí)，授課對(duì)象為高一年級(jí)學(xué)生.

除教學(xué)模塊上的調(diào)整之外，教學(xué)內(nèi)容的安排也有了較大的變化.舊教材第一課同時(shí)學(xué)習(xí)充分條件、必要條件和充要條件，第二課主要為鞏固概念與提升應(yīng)用；新教材第一課只學(xué)習(xí)充分條件和必要條件，第二課學(xué)習(xí)充要條件.新教材在教學(xué)目標(biāo)上突出了素養(yǎng)導(dǎo)向，更重視培養(yǎng)學(xué)生的邏輯推理能力與數(shù)學(xué)表達(dá)能力，在教學(xué)內(nèi)容上更重視把握數(shù)學(xué)本質(zhì).

由于這些變化，給一線教師的教學(xué)設(shè)計(jì)帶來許多困惑，也是一種挑戰(zhàn).首先，初中數(shù)學(xué)知識(shí)比較具體，高中數(shù)學(xué)知識(shí)相對(duì)抽象.面對(duì)剛進(jìn)入高中學(xué)習(xí)的新生，如何使其理解抽象的數(shù)學(xué)概念，并滲透培養(yǎng)其應(yīng)用概念進(jìn)行論證的數(shù)學(xué)能力，順利完成教學(xué)目標(biāo)？其次，充分條件和必要條件是相伴而生的兩個(gè)邏輯關(guān)系，將這兩個(gè)條件放在一起判斷，更有利于學(xué)生對(duì)兩個(gè)條件之間邏輯關(guān)系的理解.如何兼顧教材安排和教學(xué)內(nèi)容的邏輯關(guān)系？

要解決上面兩個(gè)困惑，本課教學(xué)中的問題設(shè)計(jì)、教學(xué)環(huán)節(jié)設(shè)計(jì)與師生互動(dòng)設(shè)計(jì)都需要進(jìn)行一次整合，使得學(xué)習(xí)既符合概念的邏輯關(guān)系，也符合學(xué)生認(rèn)知特點(diǎn).下面是筆者的具體設(shè)計(jì)，如有不足之處，望同行批評(píng)指正.

3 教學(xué)重構(gòu)

第一課的設(shè)計(jì)，首先，考慮到充分條件與必要條件相伴而生，從邏輯關(guān)系的角度上，應(yīng)該同時(shí)給與判斷，故將例1、例2的學(xué)習(xí)目標(biāo)合并起來；其次，結(jié)合判斷，要求學(xué)生對(duì)這兩種條件的邏輯關(guān)系有深刻的認(rèn)知，因此對(duì)引例與問題的設(shè)計(jì)從正反兩個(gè)方向反復(fù)咀嚼，幫助學(xué)生更透徹地厘清充分條件與必要條件的含義與聯(lián)系；最后，在學(xué)生充分理解其含義之后，再設(shè)置判定定理與充分條件、性質(zhì)定理與必要條件關(guān)系的探究問題，有利于學(xué)生從邏輯關(guān)系的角度理解探究結(jié)果.

第二節(jié)課的設(shè)計(jì)，充分挖掘教材中思考、探究和例題之間的聯(lián)系，以“判斷充要條件的邏輯過程”為聯(lián)系的紐帶，問題逐層鋪墊引導(dǎo)，讓學(xué)生體會(huì)應(yīng)從正逆兩個(gè)方向判斷的邏輯思維，將邏輯推理素養(yǎng)的培養(yǎng)滲透在問題解決的各個(gè)環(huán)節(jié)之中.

基于上述分析，教學(xué)流程如下：

第一課：判斷命題真假，p與q關(guān)系的符號(hào)化應(yīng)用，充分條件的定義與判斷，探究q與p的辯證關(guān)系，必要條件的定義與判斷，充分條件與必要條件的定義與相互關(guān)系，探究判定定理與充分條件、性質(zhì)定理與必要條件關(guān)系，統(tǒng)總與提升.

第二課：判斷原命題與逆命題真假，充要條件的定義，感受正逆兩個(gè)方向判斷充要條件，從正逆兩個(gè)方向探究其他三種邏輯關(guān)系，充要條件的實(shí)際應(yīng)用，從正逆兩個(gè)方向探究定義與充要條件關(guān)系，證明充要條件.

4 具體設(shè)計(jì)

4.1 第一課設(shè)計(jì)要點(diǎn)

(一) 前后銜接、概念引入

例1指出下列“若p，則q”形式命題中的p與q，判斷哪些是真命題？哪些是假命題？

(1) 若平行四邊形的對(duì)角線互相垂直，則這個(gè)平行四邊形是菱形；

(2) 若兩個(gè)三角形的周長相等，則這兩個(gè)三角形全等；

(3) 若a=b，則ac=bc；

(4) 若x=1，則x2=1；

(5) 若平面內(nèi)兩條直線a和b均垂直于直線l，則a∥b.

設(shè)計(jì)意圖：鞏固命題中的p與q，以命題的真假為載體，引出p和q的符號(hào)關(guān)系.

(二) 問題引領(lǐng)、概念形成

1. 逐層設(shè)問、感知概念

若命題“若p，則q”為真，即p經(jīng)過推理可以得出q，這時(shí)我們就說，p可以推出q，記作p?q，若命題“若p，則q”為假，則p不能推出p，記作p?/q.

問題1請(qǐng)你利用p?q，p?/q表示上面命題中p與q的關(guān)系.

若p?q，即當(dāng)p成立時(shí)，足夠充分保證q成立，此時(shí)稱p是q成立的充分條件；若p?/q，即當(dāng)p成立時(shí)，不足以保證q成立，此時(shí)稱p不是q成立的充分條件.

問題2從“充分條件”的角度上，說一說上面命題中p與q的關(guān)系.

問題3在p?q的前提下，q一定可以推出p嗎？

問題4問題3的基礎(chǔ)上，當(dāng)q不成立時(shí)，p成立嗎？

雖然，當(dāng)p能推出q時(shí)，q不一定能推出p，但當(dāng)q不成立時(shí)，p一定不成立，q是p成立的必不可少的條件，因此，我們稱q是p的必要條件.

設(shè)計(jì)意圖：按照研究步驟(p與q的符號(hào)關(guān)系→p與q的充分條件關(guān)系→q與p的關(guān)系探究→q與p的必要條件關(guān)系)設(shè)計(jì)四個(gè)問題.從文字語言到符號(hào)語言，從符號(hào)語言到概念理解，逐步培養(yǎng)用數(shù)學(xué)的邏輯思維思考問題、用數(shù)學(xué)的邏輯用語表達(dá)問題的能力.問題3和問題4的連環(huán)設(shè)計(jì)，幫助學(xué)生理解“必要條件”的含義，同時(shí)，讓學(xué)生感受辯證思維的應(yīng)用，促進(jìn)其邏輯推理素養(yǎng)的提升.

2. 水到渠成、概念形成

介紹充分條件與必要條件的概念與邏輯聯(lián)系.

(三)解決問題、內(nèi)化概念

例2下列“若p，則q”形式的命題中，哪些命題中的p是q的充分條件，同時(shí)，q是p的必要條件？

(1) 若四邊形的兩組對(duì)角分別相等，則這個(gè)四邊形是平行四邊形；

(2) 若兩個(gè)三角形的三邊成比例，則這兩個(gè)三角形相似；

(3) 若x2-4x+3=0，則x=1；

(4) 若x，y為無理數(shù)，則xy為無理數(shù)；

(5) 若兩個(gè)三角形全等，則它們的周長相等.

(四) 探究問題、升華概念

探究1命題“若四邊形的兩組對(duì)角分別相等，則這個(gè)四邊形是平行四邊形”中，給出了“四邊形是平行四邊形”的一個(gè)充分條件，即“四邊形的兩組對(duì)角分別相等”.這樣的充分條件唯一嗎？你能再給幾個(gè)嗎？

總結(jié)：(1) 寫充分條件，就是寫一個(gè)條件，使得其可以推出q；(2) 使得q成立的充分條件p是不唯一的；(3) 判定定理都給出了相應(yīng)結(jié)論的一個(gè)充分條件.

問題5你能寫出幾個(gè)使“三角形相似”成立的充分條件嗎？

探究2命題“若兩個(gè)三角形全等，則它們的周長相等”中，給出了“兩個(gè)三角形全等”的一個(gè)必要條件，即“它們的周長相等”.這樣的必要條件唯一嗎？你能再給幾個(gè)嗎？

總結(jié)：(1) 寫必要條件，就是寫p可以得到的一個(gè)正確結(jié)論；(2) 給定條件p，由p可以推出的必要條件q是不唯一的；(3) 性質(zhì)定理的結(jié)論都是給出了一個(gè)必要條件.

問題6你能寫出幾個(gè)使“三角形相似”成立的必要條件嗎？

探究3寫出使“x>2”成立的一個(gè)充分條件，寫出使“x>2”成立的一個(gè)必要條件.

設(shè)計(jì)意圖：探究1和探究2目的在于加深對(duì)“充分條件”和“必要條件”含義的理解，并幫助學(xué)生理解判定定理與充分條件、性質(zhì)定理與必要條件的關(guān)系.探究3則進(jìn)一步提升學(xué)生數(shù)學(xué)抽象、邏輯推理素養(yǎng)，從具體上升到抽象，研究“x>2”的充分條件和必要條件，從概念的角度上再認(rèn)識(shí)“充分條件”和“必要條件”.

4.2 第二課設(shè)計(jì)要點(diǎn)

(一) 前后銜接、概念引入

例3下列“若p，則q”形式的命題中，哪些命題與它的逆命題都是真命題？

(1) 若兩個(gè)三角形的兩角和其中一角所對(duì)的邊分別相等，則這兩個(gè)三角形全等；

(2) 若兩個(gè)三角形全等，則這兩個(gè)三角形的周長相等；

(3) 若一元二次方程ax2+bx+c=0有兩個(gè)不相等的實(shí)數(shù)根，則ac<0；

(4) 若A∪B是空集，則A與B均是空集.

問題7命題(1)中，p是q的什么條件，為什么？

設(shè)計(jì)意圖引導(dǎo)學(xué)生，利用充分條件和必要條件的定義，從正逆兩個(gè)方向判定p與q的關(guān)系，引出充要條件的定義.

(二)問題引領(lǐng)、概念形成

介紹充要條件的定義(略).

1. 逐層設(shè)問、感知概念

問題8若p是q的充要條件時(shí)，q是p的什么條件？

問題9以上命題中還有充要條件嗎？

問題10命題(2)(3)中p是q的什么條件?嘗試論證.

問題11命題(2)(3)中q是p的什么條件?嘗試論證.

問題12除了上述幾個(gè)關(guān)系外，p與q還有其他關(guān)系嗎?相應(yīng)的原命題和逆命題真假是怎樣的？

2. 水到渠成、概念完善

介紹充要條件、充分不必要條件、必要不充分條件和既不充分也不必要條件.(略)

設(shè)計(jì)意圖：逐層設(shè)問，引導(dǎo)學(xué)生利用充分條件和必要條件的定義，發(fā)現(xiàn)p與q的關(guān)系，感受相伴而生的q與p的關(guān)系.并利用定義口述論證關(guān)系，培養(yǎng)學(xué)生數(shù)學(xué)論證能力、辯證思維與嚴(yán)謹(jǐn)?shù)目茖W(xué)精神，促進(jìn)邏輯推理素養(yǎng)的提升，同時(shí)為定義與充要條件的關(guān)系及充要條件的證明做好鋪墊.

(三) 解決問題、應(yīng)用概念

例4下列各命題中，p是q的什么條件，同時(shí)，q是p的什么條件？

(1)p：四邊形是正方形，q：四邊形的對(duì)角線互相垂直且平分；

(2)p：兩個(gè)三角形相似，q：兩個(gè)三角形三邊成比例；

(3)p：xy>0，q：x>0，y>0；

(4)p：x=1是一元二次方程ax2+bx+c=0的一個(gè)根，q：a+b+c=0.

(四) 探究問題、內(nèi)化概念

探究4請(qǐng)給出“四邊形是平行四邊形”的一個(gè)充要條件，并嘗試論證.

問題13你還能給出其他“四邊形是平行四邊”的充要條件，并簡單論證嗎？

結(jié)論1：寫結(jié)論q的一個(gè)充要條件p，其應(yīng)滿足兩方面，即p能推出q，反之，q也能推出p.

結(jié)論2：我們可以利用充要條件給出一個(gè)概念的定義.

問題14請(qǐng)你利用充要條件給出“兩個(gè)三角形全等”的定義.

結(jié)論3：由于定義是充要條件，因此要給出定義必須滿足兩個(gè)方面，p?q，q?p，即p?q.

設(shè)計(jì)意圖：進(jìn)一步應(yīng)用充分條件和必要條件的定義論證充要條件，感受定義的充要性，區(qū)分條件p與結(jié)論q，為證明充要條件做好準(zhǔn)備.

5 教學(xué)體會(huì)

兩課依照小單元結(jié)構(gòu)設(shè)計(jì)，第一課為第二課鋪墊，符合知識(shí)“螺旋上升”的學(xué)習(xí)方式.

“必要條件”是學(xué)生學(xué)習(xí)的難點(diǎn)，在以往的學(xué)習(xí)中多數(shù)學(xué)生不理解“必要”的意義，只能通過“名詞記背”的方式學(xué)習(xí)這個(gè)概念.第一課中問題3、4針對(duì)“必要”的意義而設(shè)計(jì)，讓學(xué)生感受到了“雖然，q成立時(shí)，p不一定成立，但是，當(dāng)q不成立時(shí)，p一定不成立，q是p成立的必不可少的條件”.

“證明充要條件”也是學(xué)生學(xué)習(xí)的難點(diǎn)，在以往的學(xué)習(xí)中學(xué)生不理解為什么要從“充分性”和“必要性”兩個(gè)方面證明，作業(yè)通常也只證一個(gè)方面，根本原因是對(duì)“充要條件”的邏輯關(guān)系理解不夠深入.第二課的例題和問題均要求學(xué)生從兩個(gè)方面口述論證，培養(yǎng)學(xué)生的“邏輯”意識(shí).通過學(xué)習(xí)的深入，學(xué)生從“被牽引式論證”，到“意識(shí)到兩方面論證的需要”，數(shù)學(xué)思維的辯證性和邏輯性得到發(fā)展.

兩課均突出了“以學(xué)為主，以教為輔，有數(shù)學(xué)味”的理念.首先，問題面向“學(xué)習(xí)需要”而設(shè)計(jì)，符合學(xué)生的最近發(fā)展區(qū)，因此課堂有效互動(dòng)頻繁；其次，問題符合數(shù)學(xué)學(xué)科特點(diǎn)，具有邏輯性、辯證性和科學(xué)性，利于學(xué)生數(shù)學(xué)核心素養(yǎng)的提升；最后，學(xué)生互動(dòng)間產(chǎn)生了許多有趣的結(jié)論，將學(xué)習(xí)逐漸引向深入，課堂目標(biāo)達(dá)成度高.