特殊到一般 具體到抽象
——以一道幾何探究題為例

何 偉

(上海外國(guó)語(yǔ)大學(xué)蘇河灣實(shí)驗(yàn)中學(xué),200071)

數(shù)學(xué)學(xué)習(xí)來(lái)源于解決問(wèn)題的過(guò)程,解題需要的是思維能力和數(shù)學(xué)方法.對(duì)探究性問(wèn)題的深入思考和不斷嘗試,能夠幫助學(xué)生更好地完善知識(shí)體系、提升思維能力、徹底理解數(shù)學(xué)思想方法,最終形成良好的認(rèn)知結(jié)構(gòu)和解決問(wèn)題的核心能力.本文從一道幾何探究題入手,闡述如何在探究過(guò)程中,體現(xiàn)由特殊到一般、由具體到抽象的數(shù)學(xué)方法.

一、問(wèn)題提出

由小正方形組成的長(zhǎng)方形的對(duì)角線(xiàn)所穿越的小正方形個(gè)數(shù)研究:

不難發(fā)現(xiàn),由6×2個(gè)小正方形組成的長(zhǎng)方形,它的對(duì)角線(xiàn)穿過(guò)6個(gè)小正方形(如圖1).由7×5個(gè)小正方形組成的長(zhǎng)方形,它的對(duì)角線(xiàn)穿過(guò)11個(gè)小正方形(如圖2).

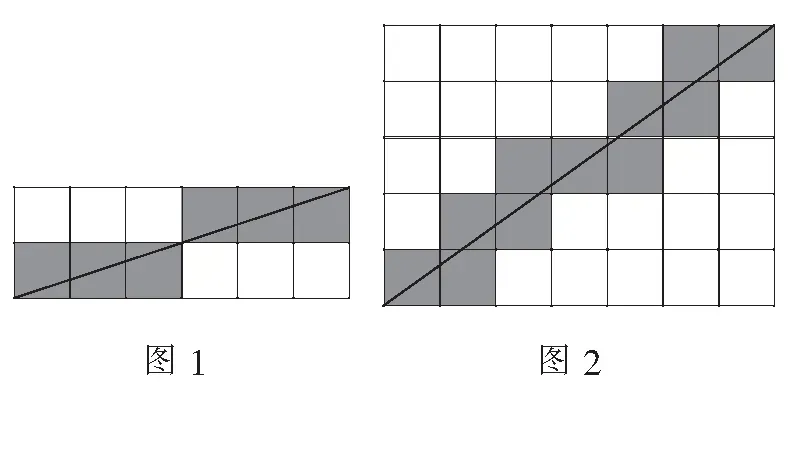
問(wèn)題(1)由2022×120個(gè)小正方形組成的長(zhǎng)方形,它的對(duì)角線(xiàn)穿過(guò)多少個(gè)小正方形?

(2)能否給出由m×n個(gè)(其中m,n是正整數(shù))小正方形組成的長(zhǎng)方形,它的對(duì)角線(xiàn)穿過(guò)的小正方形個(gè)數(shù)的計(jì)算公式,并說(shuō)明理由.

(3)能否將上述結(jié)論推廣成由m×n×h(其中m,n,h是正整數(shù))個(gè)小立方體組成的長(zhǎng)方體,它的對(duì)角線(xiàn)穿過(guò)的小立方體的個(gè)數(shù)?

二、問(wèn)題分析

長(zhǎng)方形由m×n個(gè)(其中m,n是正整數(shù))小正方形組成，如何來(lái)計(jì)算它的對(duì)角線(xiàn)穿過(guò)的小正方形數(shù)量呢?

從特殊情況入手:

1.m=n(如圖3～圖4);

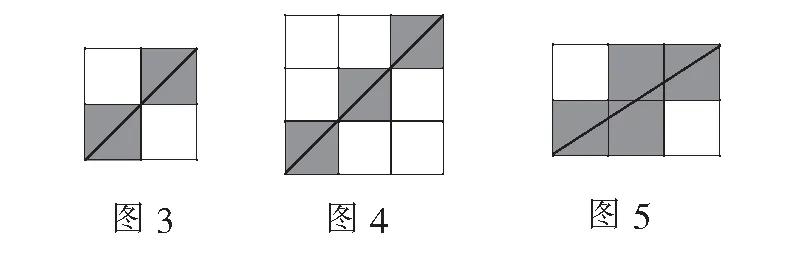
2.gcd(m,n)=1(如圖5～圖6);

3.gcd(m,n)>1(圖7～圖8),其中g(shù)cd(m,n)表示m,n的最大公約數(shù).

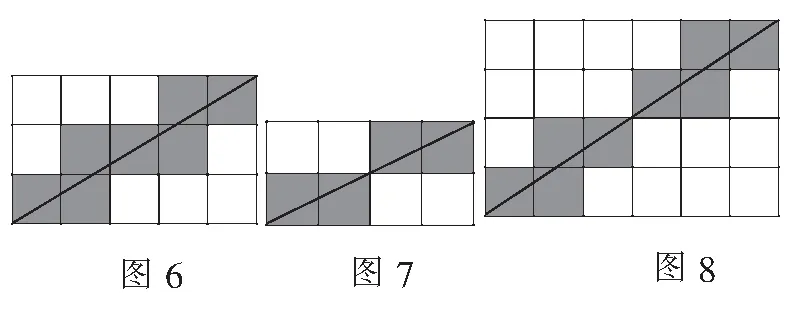
對(duì)三種情況進(jìn)行研究,可得f(對(duì)角線(xiàn)穿過(guò)的小正方形數(shù)量)與m,n的關(guān)系(見(jiàn)表1).

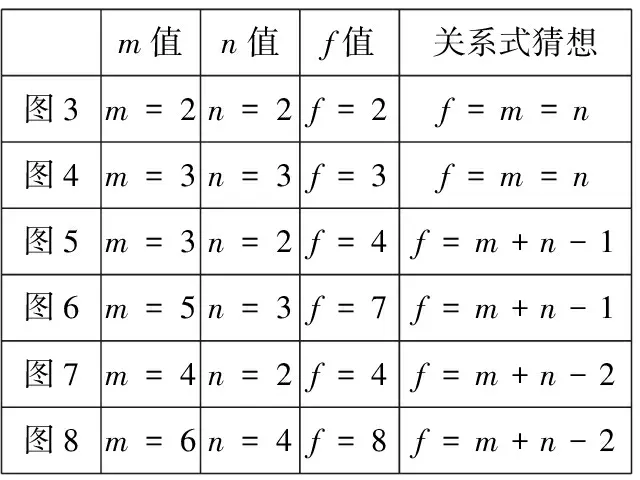
表1

由表1，可提出如下猜想:長(zhǎng)方形由m×n個(gè)(其中m,n是正整數(shù))小正方形組成,它的對(duì)角線(xiàn)穿過(guò)的小正方形數(shù)量f=m+n-gcd(m,n).

三、結(jié)論驗(yàn)證

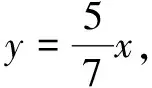
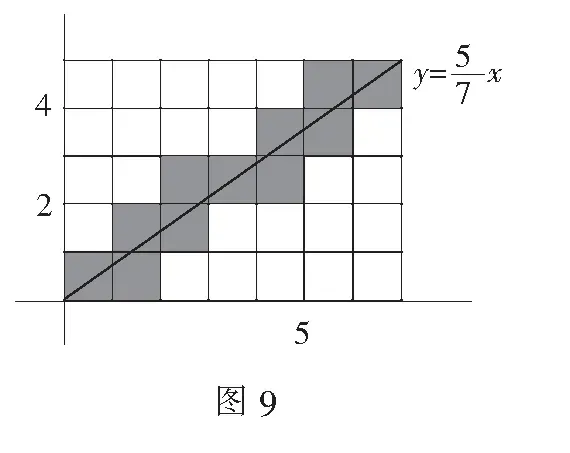
(2)對(duì)角線(xiàn)與m+1條豎直線(xiàn)有m+1個(gè)交點(diǎn),與n+1條水平線(xiàn)有n+1個(gè)交點(diǎn),由于對(duì)角線(xiàn)的兩個(gè)端點(diǎn)被重復(fù)計(jì)算,所以對(duì)角線(xiàn)與所有格線(xiàn)共有(m+1)+(n+1)-2=m+n個(gè)交點(diǎn),且除去兩端端點(diǎn)外,其余的交點(diǎn)坐標(biāo)(a,b)中有且只有一個(gè)數(shù)值為整數(shù),0≤a≤m,0≤b≤n.

(3)這m+n個(gè)交點(diǎn)將對(duì)角線(xiàn)分為(m+n-1)段,每一小段都與穿越它的小方格一一對(duì)應(yīng),所以對(duì)角線(xiàn)共穿過(guò)了(m+n-1)個(gè)小方格,即滿(mǎn)足猜想公式f=m+n-gcd(m,n)，此時(shí)gcd(m,n)=1.

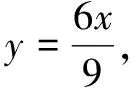
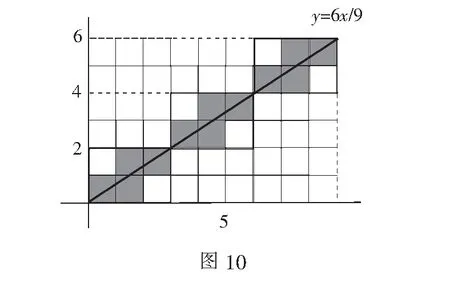
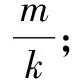
綜上所述,長(zhǎng)方形由m×n個(gè)(其中m,n是正整數(shù))小正方形組成,其對(duì)角線(xiàn)穿過(guò)的小正方形數(shù)量f=m+n-gcd(m,n),無(wú)論m與n的數(shù)量關(guān)系如何均滿(mǎn)足此公式.

四、問(wèn)題解決

對(duì)于問(wèn)題(1),因?yàn)間cd(2022,120)=6,所以由2022×120個(gè)小正方形組成的長(zhǎng)方形,它的對(duì)角線(xiàn)穿過(guò)的小正方形數(shù)量f=m+n-gcd(m,n)=2022+120-6=2136.

五、特殊問(wèn)題一般化、具體問(wèn)題抽象化

接下來(lái),我們將上述結(jié)論推廣到由m×n×h(其中m,n,h是正整數(shù))個(gè)小立方體組成的長(zhǎng)方體中,它的對(duì)角線(xiàn)穿過(guò)的小立方體的個(gè)數(shù).

在平面十字坐標(biāo)系中,筆者在解決“由m×n個(gè)(其中m,n是正整數(shù))小正方形組成的長(zhǎng)方形中,它的對(duì)角線(xiàn)穿過(guò)的小正方形個(gè)數(shù)的計(jì)算公式”是通過(guò)計(jì)算對(duì)角線(xiàn)分別與橫格線(xiàn)、豎格線(xiàn)的交點(diǎn)數(shù),來(lái)計(jì)算對(duì)角線(xiàn)的分段數(shù),從而找出所穿越的小方格數(shù)量,得出f=m+n-gcd(m,n)的結(jié)論.

經(jīng)分析,不難發(fā)現(xiàn)公式f=m+n-gcd(m,n)形似容斥原理公式,即對(duì)于長(zhǎng)方形的對(duì)角線(xiàn)每穿越一次縱、橫格線(xiàn)時(shí)產(chǎn)生一個(gè)交點(diǎn),其在十字坐標(biāo)系內(nèi)坐標(biāo)為(a,b),0≤a≤m,0≤b≤n,a,b中至少有一個(gè)數(shù)值為整數(shù),這些交點(diǎn)將對(duì)角線(xiàn)分段,分段數(shù)為f(m∪n)=m+n-m∩n(如圖11).

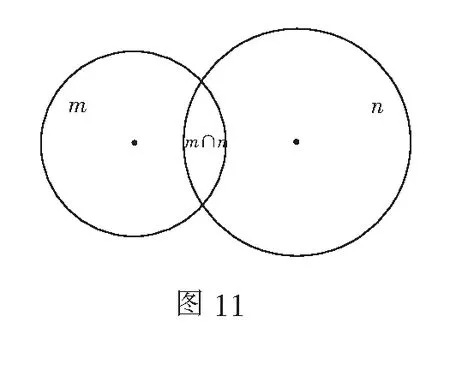
而在立體三維坐標(biāo)系中,想象由m×n×h(其中,m,n,h是正整數(shù))個(gè)小立方體組成的長(zhǎng)方體中,體對(duì)角線(xiàn)所穿越的將是內(nèi)部小立方體的頂點(diǎn)、棱和面.由前文中的平面體系證明，不難發(fā)現(xiàn)如下結(jié)論:

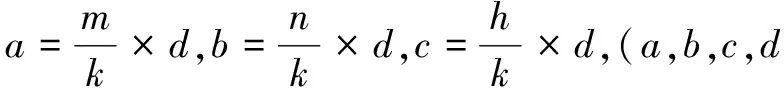
2.當(dāng)體對(duì)角線(xiàn)穿越內(nèi)部小立方體棱上某點(diǎn)(棱兩端端點(diǎn)除外)的時(shí)候,必有棱所交界的兩個(gè)方向產(chǎn)生大于1的最大公約數(shù)的整數(shù)倍,即坐標(biāo)(a,b,c)中必有2個(gè)數(shù)值為整數(shù),此時(shí)體對(duì)角線(xiàn)可穿越2個(gè)數(shù)值為整數(shù)值的坐標(biāo)點(diǎn)后進(jìn)入一個(gè)新小立方體.

3.當(dāng)體對(duì)角線(xiàn)穿越內(nèi)部小立方體面上某點(diǎn)(四周棱上點(diǎn)除外)的時(shí)候,必有點(diǎn)的坐標(biāo)(a,b,c)中有且只有1個(gè)數(shù)值為整數(shù),而且每穿過(guò)一個(gè)面,就可以到達(dá)一個(gè)新的小立方體.

例如,由 9×5×6個(gè)小立方體組成的長(zhǎng)方體,其三視圖如圖12所示.

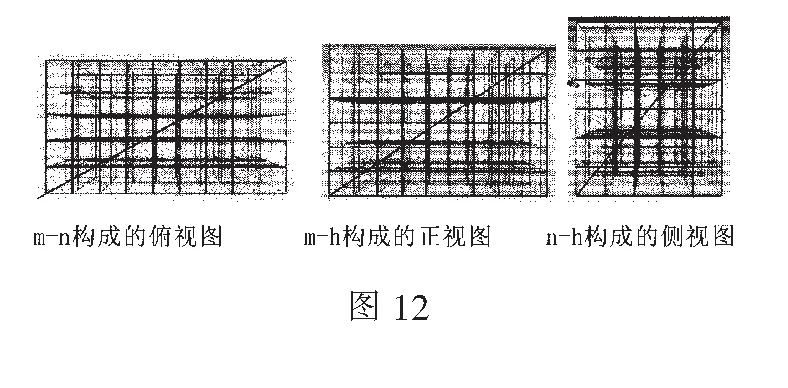
因?yàn)間cd(9,5,6)=1,所以體對(duì)角線(xiàn)沒(méi)有直接穿越小立方體頂點(diǎn);

因?yàn)間cd(9,6)=3,所以在m-h構(gòu)成的正視圖中,體對(duì)角線(xiàn)在長(zhǎng)方體內(nèi)部2次穿越小立方體的棱(不包括兩端端點(diǎn));

因?yàn)間cd(9,5)=1,gcd(5,6)=1,所以在m-n構(gòu)成的俯視圖、n-h構(gòu)成的側(cè)視圖中體對(duì)角線(xiàn)無(wú)穿越內(nèi)部小立方體棱,均穿越面到達(dá)新的小立方體.

經(jīng)過(guò)作圖計(jì)數(shù)得到體對(duì)角線(xiàn)穿越小立方體數(shù)量是:

9+5+6-gcd(9,6)-gcd(9,5)-gcd(5,6)+gcd(9,5,6)=16(個(gè))

由上分析,可以將問(wèn)題轉(zhuǎn)化為體對(duì)角線(xiàn)在立體坐標(biāo)系中與小立方體面、棱、頂點(diǎn)的所有交點(diǎn)坐標(biāo)(a,b,c),已知0≤a≤m,0≤b≤n，0≤c≤h,至少有一個(gè)數(shù)值為整數(shù),即可計(jì)入穿越一個(gè)新的立方體.

因此,由m×n×h(其中m,n,h是正整數(shù))個(gè)小立方體組成的長(zhǎng)方體,它的體對(duì)角線(xiàn)穿過(guò)小立方體個(gè)數(shù)F的計(jì)數(shù)公式為:

F=m+n+h-gcd(m,n)-gcd(m,h)-gcd(n,h)+gcd(m,n,h).

同樣,上述公式也形似容斥原理公式m+n+h-m∩n-m∩h-n∩h+m∩n∩h.

六、反思

問(wèn)題(1)中給出具體的行和列的數(shù)字,計(jì)算出對(duì)角線(xiàn)穿過(guò)的正方形,便于上手解決該問(wèn)題,通過(guò)一般化、具體化的問(wèn)題,找出相同點(diǎn)和不同點(diǎn),從而推導(dǎo)出公式;問(wèn)題(2)遞進(jìn)到一般化的m×n個(gè)(其中m,n是正整數(shù))小正方形組成的長(zhǎng)方形中,它的對(duì)角線(xiàn)穿過(guò)的小正方形個(gè)數(shù)的計(jì)算公式,需要找出行列數(shù)互素以及不互素情況下如何用一個(gè)公式來(lái)表示;問(wèn)題(3)更進(jìn)一步,從平面上升到立體,需要推導(dǎo)出長(zhǎng)方體對(duì)角線(xiàn)穿過(guò)的正方體個(gè)數(shù)的公式.該探究題由具體數(shù)字到抽象字母,從平面圖形到立體圖形的延伸,開(kāi)闊了學(xué)生的視野，激發(fā)了學(xué)生的數(shù)學(xué)思維.