作圖無定法 要旨系得法
——以網格作圖中的軸對稱為例

雷改良

(湖北省武漢經濟技術開發區第二中學,430056)

近幾年中考網格作圖經常出現軸對稱的影子.相較于網格作圖中的作分點、作垂線、作平移、作角平分線而言,網格中的作對稱要稍微難一點.很多問題不是直接要我們作對稱,而是將對稱性的作圖意圖雜糅在頗為棘手的看似與對稱無關的問題里面,導致學生對作圖的核心把握不準,更不能將平時提煉的基本模型直接運用到該問題上.本文分類例說如何利用作對稱的常用策略解決網格的有關經典作圖問題.

一、作對稱的常用策略

策略1利用軸對稱性質直接作對稱

例1如圖1～圖3,作點A關于MN的對稱點.

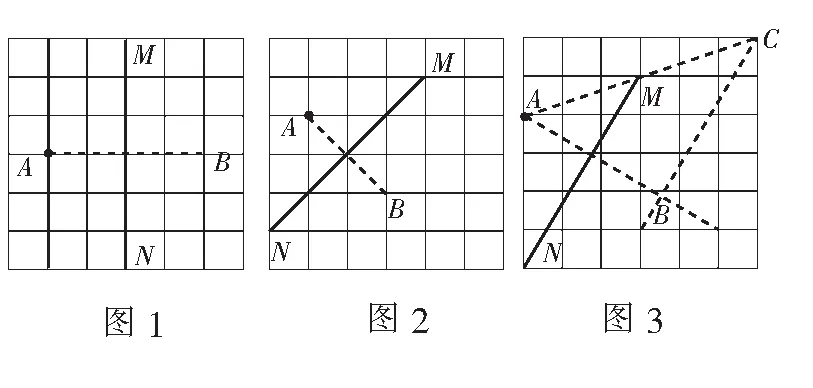
基本方法對稱軸是任何一對對稱點所連線段的垂直平分線.

分析先過點A作對稱軸的垂線,垂足是格點(如圖1～圖2)，則直接倍長.若垂足不是格點,則可想辦法構造中位線模型,如圖3,連結AM并將其倍長至點C,再過C作對稱軸MN的平行線交對稱軸的垂線于一點B即為所求.

例2如圖4,?ABC是邊長為1正方形網格中的格點三角形.

(1)畫點A關于BC的對稱點D;

(2)連結AD交BC于E點,畫點E關于AC的對稱點F.

分析(1)過點A作對稱軸BC的垂線,垂足不是格點,則先將AB倍長至點M,再過點M作對稱軸BC的平行線交對稱軸的垂線于點D即為所求.

(2)因為點E為非格點,且∠BAC=45°，則可利用后面的策略3,構造?ACH與?ACB全等,再作CH邊上的高AF,即可得點E關于AC的對稱點F.

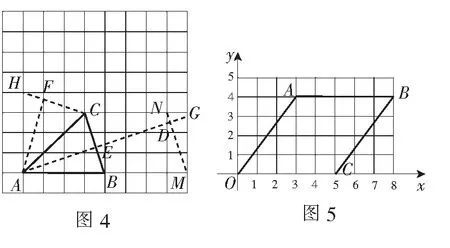
策略2利用對稱軸作對稱

例3(2020年武漢中考題)在8×5的網格中建立如圖5的平面直角坐標系,四邊形OABC的頂點坐標分別為O(0,0),A(3,4),B(8,4),C(5,0).僅用無刻度的直尺在給定網格中按下列步驟完成畫圖,并回答問題:

(1)將線段CB繞點C逆時針旋轉90°,畫出對應線段CD;

(2)在線段AB上畫點E,使∠BCE=45°(保留畫圖過程的痕跡);

(3)連結AC,畫點E關于直線AC的對稱點F,并簡要說明畫法.

基本方法軸對稱圖形兩對對稱點交叉相連的交點在對稱軸上.

分析第(1)、(2)問如圖6.第(3)問,因為四邊形ABCD是菱形,則對角線AC為對稱軸,且點O與點B關于AC對稱,連結OE與對稱軸AC交于點M,連結BM并延長與AO的交點即為所求的對稱點F(如圖7).

策略3利用全等作對稱

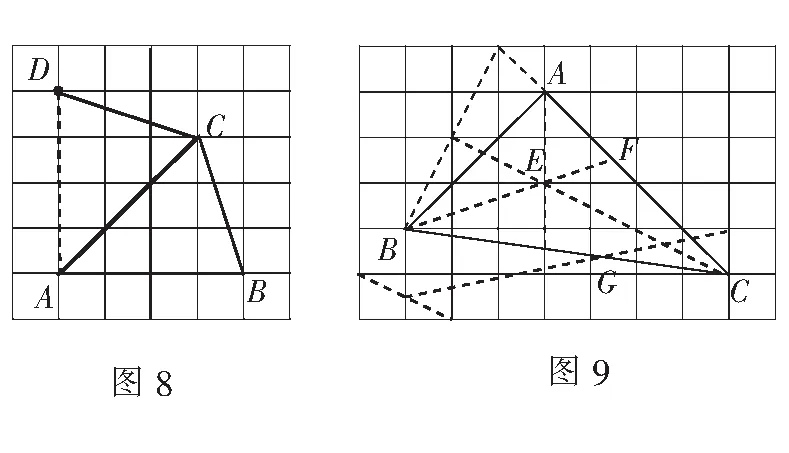
例4圖8是由邊長為1的小正方形構成的網格,每個小正方形的頂點叫做格點.?ABC的頂點在格點上,僅用無刻度尺的直尺在給定網格中畫圖,畫圖過程用虛線表示,畫圖結果用實線表示,按步驟畫出BC關于AC對稱的線段CD.

基本方法由點或線段所在三角形的對稱圖形,得到相應的對稱點或對稱邊.

分析易知∠BAC=45°.如圖8,構造?ACD與?ACB全等,即可得CB關于AC對稱的線段CD.

例5如圖9,?ABC是邊長為1正方形網格中的格點三角形.

(1)畫?ABC的角平分線BF;

(2)畫點A關于BF的對稱點G.

分析(1)利用三角形三個角平分線交于一點的性質.如圖9,作出∠BAC和∠ACB的角平分線的交點E,連結BE并延長交AC于點F，BF即為?ABC的角平分線.

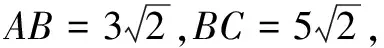
二、常用策略應用

類型1利用對稱求最值

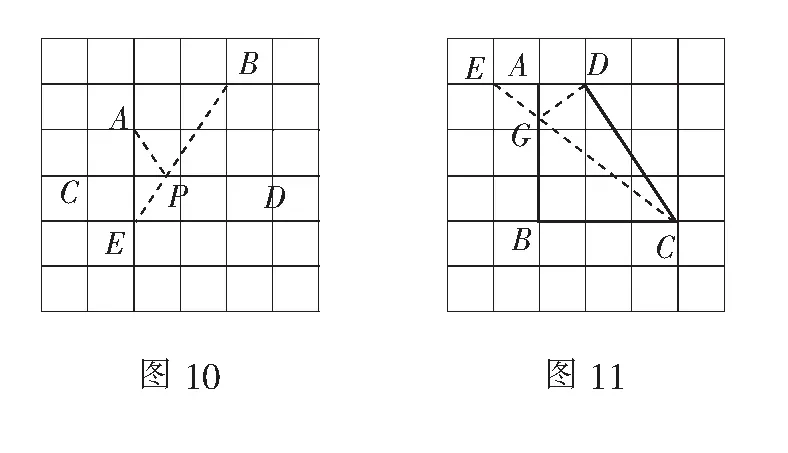
例6如圖10,在CD上確定一點P,使PA+PB的值最小.

分析本題求最值,本質則是作對稱.如圖10,利用策略1,找到點A關于CD的對稱點E,連結BE交CD于點P即為所求.

類型2利用對稱作角相等

例7(2019年武漢中考題改編)圖11是由邊長為1的小正方形構成的網格,每個小正方形的頂點叫做格點.四邊形ABCD的頂點在格點上,請選擇適當的格點,用無刻度的直尺在邊AB上畫一點G,使∠AGD=∠BGC.(保留連線的痕跡,不要求說明理由)

分析要找到滿足條件的點G,使∠AGD=∠BGC,可利用策略1.如圖11,作D點關于AB的對稱點E,連結CE交AB于點G即為所求.

類型3利用對稱作線段相等

例8如圖12,?ABC中,AB=AC,B,C為格點.

(1)P為邊AB上一點,用無刻度直尺在AC上找一點Q,使AQ=AP；

(2)M為BC上任意一點,在BC上找一點N，使CN=BM.

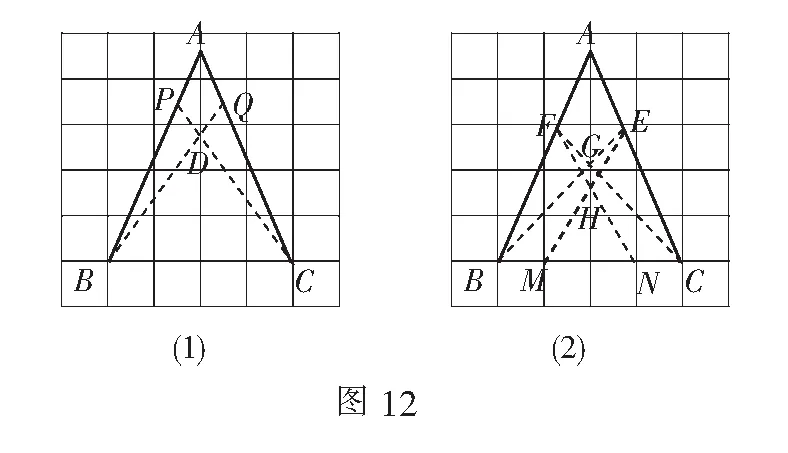
分析(1)此問可利用策略2解決.如圖12(1),連結CP交對稱軸于點D,連結BD并延長與AC的交點Q即為所求.

(2)可仿照問題(1),先在AC上取點E,在AB上找到點E關于對稱軸的對稱點F,再連結ME,與對稱軸交于點H,連結FH并延長與BC的交點即為N(如圖12(2)).

類型4利用對稱作全等

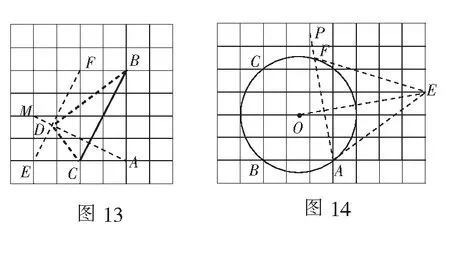
例9如圖13,點A,B,C都在格點上,僅用無刻度的直尺,將?ABC沿BC邊翻折,畫出翻折后的?DBC.

分析要求畫出翻折后的三角形,其核心是找到點A關于BC的對稱點D,可利用策略1解決.如圖13,先倍長AC到點E,作EF∥CB,再作BC的垂線AM,則AM與EF的交點即為點D.

類型5利用對稱作切線

例10圖14是由小正方形組成的9×7網格,每個小正方形的頂點叫做格點,A,B,C三個格點都在圓上.僅用無刻度的直尺在給定網格中完成畫圖,畫圖過程用虛線表示.

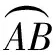
(2)畫出格點E,使EA為⊙O的一條切線,并畫出過點E的另一條切線EF,切點為F.

分析(1)略.(2)如圖14,要求畫出過點E的另一條切線EF,其核心就是作點A關于OE的對稱點.因為OE所在直線是圓O的對稱軸,只需要利用策略1,過點A作OE的垂線并延長,與圓O的交點即為點F.(因為OE為橫5.5豎1的直角三角形的斜邊,導致很多學生沒有想到過點A作橫1豎5.5的直角三角形的斜邊與OE垂直.)

三、結束語

網格作圖題靈活多變、豐富多彩,平面幾何中很多問題都能借助網格來呈現.網格自身具有的幾何特征和數值特征,使圖形的一般幾何性質得以特殊化和數量化.因此,網格作圖為學生發現問題、分析問題、解決問題提供了多角度探究的空間.網格作圖不僅能提高學生的識圖和作圖能力,還能多維度地培養學生的分析推理能力、計算能力、幾何直觀能力以及綜合運用知識解決問題的能力.

初中數學中的尺規作圖操作方法多種多樣,教學中往往只注重操作方法,缺少對作圖依據的合理闡釋,這樣會讓學生知其然而不知其所以然,一旦遇到新問題仍是束手無策.網格作圖問題其本質和常規尺規作圖相同,作圖原理并沒有發生改變,只是采用的作圖工具由直尺圓規變成了網格和無刻度的直尺,相當于是問題的載體發生了變化,因此在課堂教學中我們應更注重知識的生成過程,梳理相關內容的邏輯,幫助學生構建完善的知識體系,這樣才能有助于學生在應用知識時進行知識的正遷移.

《義務教育數學課程標準(2011年版)》指出,核心素養反映的是數學本質和數學思想,是在數學學習過程中形成的,具有綜合性、整體性和持久性.這就要求教師在課堂教學中不能按部就班地教學生獲得問題的答案,而應啟發學生挖掘問題內涵,讓學生去主動思考解決這個問題應該使用哪些學過的數學知識及數學思想方法.教師只有在平時教學中滲透這樣的數學思想方法,才能真正提高學生的數學核心素養.