立足幾何建模 領悟構造思想

劉 震

(浙江省杭州銀湖實驗中學,311422)

數學模型在初中數學教學與解題中扮演著非常重要的角色,特別是在幾何部分,通過構造數學模型,常常可以將抽象問題直觀化,復雜問題簡單化.本文介紹“手拉手”模型,并運用“手拉手”模型解決近年來中考數學中的一系列熱點難點問題,旨在深挖模型構造依據,感悟數學建模思想,培養學生的數學核心素養.

一、模型預備

1.“手拉手”全等

如圖1,已知?ABC和?ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,連結BD,CE,則?ABD≌?ACE.

此模型具有三個特征:共頂點、雙等腰、頂角相等.

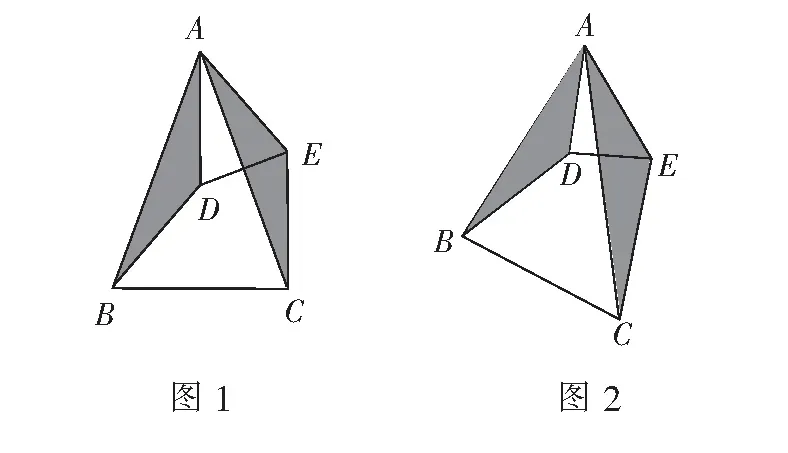
2.“手拉手”相似

如圖2,已知?ABC∽?ADE,連結BD,CE,則?ABD∽?ACE.

此模型具有三個特征:共頂點且共頂點的兩對對應邊成比例、頂角相等.

二、模型應用

1.求線段長度

例1(2014年武漢中考題)如圖3,在四邊形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,則BD的長為______.

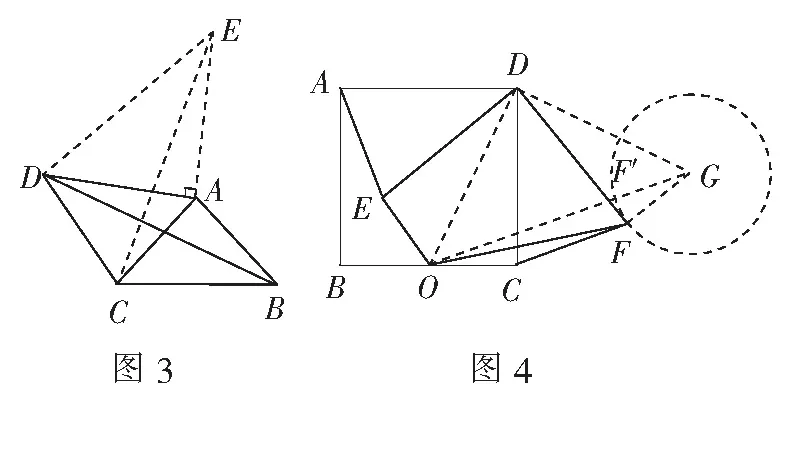
2.求線段最值

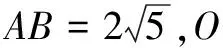
(1)求證:AE=CF;

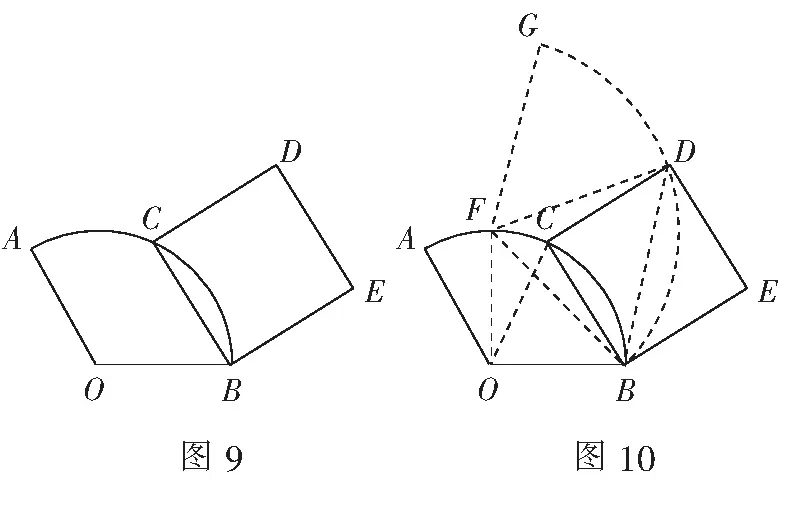
(2)若A,E,O三點共線,連結OF,求線段OF的長；

(3)求線段OF長的最小值.

解析(1)由“手拉手”全等模型,易得?ADE≌?CDF,所以AE=CF.

(2)略.

(3)如圖4,連結OD,將線段OD繞點D逆時針旋轉90°得GD,連結OG,FG.同樣,由“手拉手”全等模型,易得?GDF≌?ODE,所以GF=OE=2.

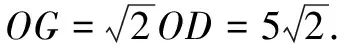
3.判定線段的數量關系

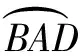
(1)求證:BD是該外接圓的直徑;

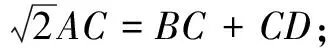
(3)若?ABC關于直線AB的對稱圖形為?ABM,連結DM,試探究DM2,AM2,BM2三者之間滿足的等量關系,并證明你的結論.

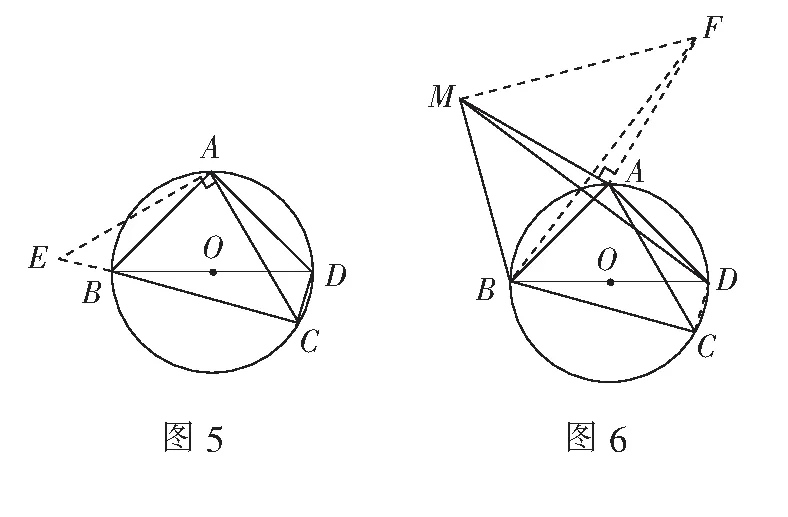
解析(1)略.

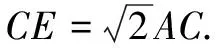
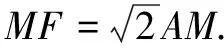
4.求面積最值

例4如圖7,在四邊形ABCD中,AD=2,CD=4.若?ABC為正三角形,則?BCD面積的最大值為______,最小值為______.

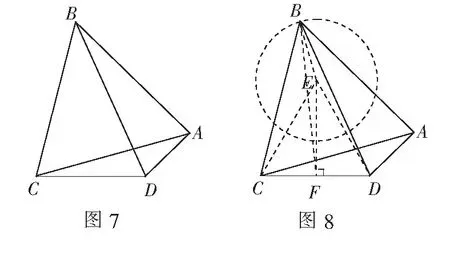
解析如圖8,以CD為邊向形內作正?CDE,連結BE.因為?ABC也為正三角形,由“手拉手”全等模型,易得?BCE≌?ACD,所以BE=AD=2.

因為?CDE位置確定,所以點E為定點,由圓的定義可知,動點B在以E為圓心,2為半徑的⊙E上運動.

5.求動點路徑長

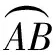
三、教學反思

1.分析條件特征,挖掘構造依據

通過構造“手拉手”模型,我們解決了初中幾何中多種類型難題.那么上述問題為什么都可以構造“手拉手”模型呢?我們不難發現,這類題目中都存在著特殊幾何圖形——“等腰三角形”“等腰直角三角形”“等邊三角形”,它們自身的幾何性質為構造“手拉手”模型提供了方便.這樣的例子有很多,如“中點”.當遇到中點時,我們應從哪些方面進行思考,進而構造出對應的模型呢?可以通過分析條件特征,挖掘模型構造依據:(1)已知一個中點,聯系條件看是否為“等腰三角形三線合一”還是“直角三角形斜邊上的中線等于斜邊的一半”.普通三角形中線可考慮“倍長中線”,有時也可考慮過中點作平行線或再取中點構造中位線以挖掘出隱含中點;(2)已知兩個中點,多為三角形中位線,若是兩中點不在一個三角形中,可考慮再構造一個中點,將分散條件集中,化隱性為顯性.

2.重視閱讀能力,培養核心素養

很多學生在閱讀題目之后沒有頭緒,缺乏思路,甚至出現理解錯誤.究其原因，一方面是因為幾何模型的綜合,有時并不會完整地展現幾何模型,而只會展現模型中最基礎的、關鍵的非連續文本或片段.這就需要我們掌握一定的非連續性文本閱讀策略以提高數學閱讀能力,進而能準確快速地捕捉到這些關鍵字眼或圖表信息,找到顯性或隱性的已知條件,并能在大腦中反應出可能的基本幾何模型,進而選出正確的做法;另一方面是因為學生的推理能力不足,邏輯思維混亂,對模型的條件、結論及推理過程不熟,也就是對圖形的數學本質沒有深入的認識和理解.因此,在解題教學中,教師應注重對試題的本質屬性,圖形的數學本質進行鉆研和挖掘,讓學生清楚知識的來龍去脈.只有這樣才能發展學生的合情推理、演繹推理能力和理性精神,培養他們的數學抽象、數學建模和直觀想象等核心素養,養成良好的數學學習品質.

3.立足幾何建模,領悟構造思想

數學建模就是根據實際問題來建立數學模型,并對數學模型進行求解,然后根據結果去解決實際問題.而數學建模思想其實是數學思想方法中的“構造法”.所謂“構造法”，就是指結合題目條件,在對條件進行深入分析的基礎上,通過數學想象構建出一個合適的數學模型,從而輔助數學解題的方法.初中數學中的很多問題都可以模型化,但在構造模型時,一要明確構造的目的, 即為什么目的而構造(對問題進行轉化化歸,化抽象為具體,化繁為簡,化難為易);二要弄清問題的特點,以便依據特點,確定方案、實現構造.正如匈牙利數學家路沙·彼得在其名著《無窮的玩藝:數學的探索與旅行》中所指出的:數學家們往往不是對問題進行正面攻擊,而是不斷將它構造、變形,直至把它轉化成能夠得到解決的問題.