基于Wellplan 的隨鉆扭矩精準模擬方法研究

羅 曼,和鵬飛,宋峙潮

（中海油能源發展股份有限公司工程技術分公司,天津 300452）

引言

扭矩是鉆完井工程的極其重要的參數,直觀的分析鉆柱、套管柱的最終地面扭矩是否在鉆機裝備的持續輸出安全扭矩范圍內,更深層次的驗證井筒清潔情況[1-5]。因此開展井筒扭矩的分析是非常必要的,可以在作業前開展工藝方案優選,提前開展預案研究。行業內也開展了較多的扭矩分析方法研究。

1 研究現狀分析與問題

薄和秋[6]等人,針對墾東大位移井從摩阻扭矩算法模型的優缺點對比出發,選擇了適合現場的軟繩模型,開展了摩阻扭矩預測。張林強[7]同樣開展了三種計算模型的對比研究,給出適合大位移井的軟繩模型算法。閆鐵[8]以三維縱橫彎曲梁理論計算了底部鉆具組合的摩阻扭矩,鉆桿段優選軟繩模型。翟鵬[9]提出了復雜結構井分段計算摩阻扭矩新模型,即按照軌跡曲率分別選擇剛性和軟繩模型。付天池[10]采用了基于軟繩累計扭矩基數的算法。劉義嶺[11]考慮鉆井液粘滯力和套管屈曲后開展了摩阻扭矩計算模型研究。丁培宇[12]以數據挖掘為手段建立了預測摩阻系數的BP 神經網絡模型。何世明[13]以小井眼長水平段為目標對象研究了摩阻扭矩的計算和控制技術。李波[14]建立了基于有限元法的三維非線性動力學模型。馬志攀[15]考慮鉆井液粘滯因素、管柱屈曲和大鉤載荷校正等因素進行了摩阻扭矩計算和套管磨損分析。張楊[16]基于套管柱下入計算了能夠通過的最大井眼曲率。唐洪林[17]以實時鉆井參數為依據,建立摩阻扭矩監測圖版。

綜上可見,均對扭矩模型開展了對比研究,軟繩模型是公認的優選模型,差異性的是對考量的因素分析不統一。目前國內海洋鉆完井通用采用Wellplan 軟件開展扭矩分析,該軟件提供了剛性和軟繩模型,存在的主要問題是,對于軟件摩阻扭矩計算考慮的影響因素的參數敏感性和確定方法存在較大差異,由此導致計算結果的誤差率較大的問題。因此開展了基于Wellplan 的扭矩影響敏感性分析和精確預測方法研究。

2 扭矩敏感性影響模型

分析扭矩敏感性,最主要的是分析扭矩如何產生的。扭矩簡單的講是管柱在井筒內橫向面相互作用產生的阻力和力臂的力矩表現,在斜井中主要由管柱和井筒內壁橫向相互摩擦作用、管柱和井內泥漿橫向相互摩擦作用以及井底鉆頭與地層垂直相互作用摩擦產生,因此可用模型表示為公式（1）

式中,T地面為井口地面顯示的總扭矩,T井壁為管柱與井壁之間產生的扭矩,T鉆井液為管柱與鉆井液之間產生的扭矩,T鉆頭為鉆頭與地層產生的扭矩。

假設管柱與井壁在某一點產生扭矩,二者必然是相互產生了接觸（接觸點一側管柱和井壁之間距離可約為0）,此時接觸的力為該點在井筒內側向力與二者摩擦系數產生的摩擦力,力臂為管柱中心到管柱外壁也就是管柱外徑的二分之一,此時管柱與井壁產生的扭矩可表示為公式（2）

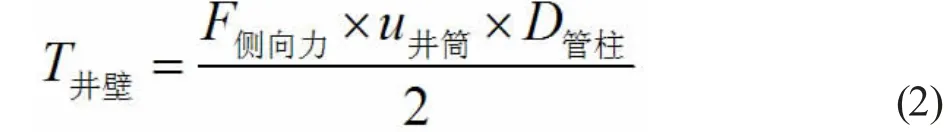
式中,F側向力為接觸點產生的管柱側向力,D管柱為管柱外徑直徑,u井筒為管柱和井壁之間的摩擦系數。

對于管柱從鉆頭以上底部開始到井口,全井筒的接觸扭矩為公式（3）,表征為從鉆頭深度md 到井口的管柱扭矩累積

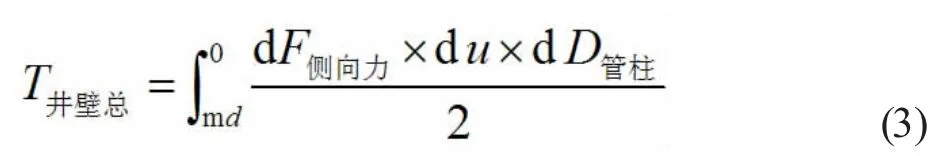
側向力的獲得,通過公式（4）。

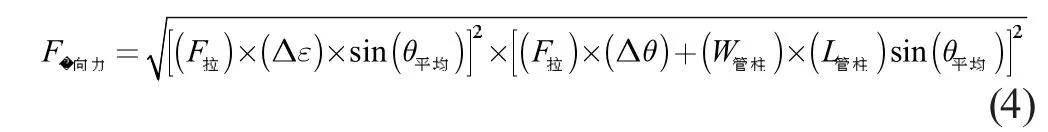
式中,F拉為該處管柱所受拉力,△ε 為計算單位內方位角的變化量,△θ 為計算單元內井斜角的變化量,θ平均為計算單元內的平均井斜角,ε平均為計算單元內的平均方位角,W管柱單位重量,L管柱為計算單元長度。

管柱與鉆井液之間相互作用產生的扭矩稱為粘滯扭矩,計算公式為（5）

式中,T 為鉆井液切力,L 管柱為管柱長度,D 管柱為管柱外徑直徑。

鉆頭扭矩模型,可理解為鉆壓導致鉆頭與井底摩擦,加上鉆頭直徑產生的力臂,得到的扭矩公式（6）

式中,μ鉆頭為鉆頭與地層之間的摩擦系數,W鉆壓為鉆壓,D鉆頭為鉆頭直徑。

3 基于Wellplan 的隨鉆扭矩預測方法應用

3.1 隨鉆扭矩精準預測工程案例：東海超深井A1s

A1s 設計完鉆井深5 040 m,定向井軌跡設計自300 m 開始造斜至745 m 達到28°,二次造斜從4 600 m 至4 850 m,造斜至40°,方位角二次造斜時左扭30°中靶,井身結構設計見表1。隨鉆采用扭矩監測、預測技術,具體方法如下。

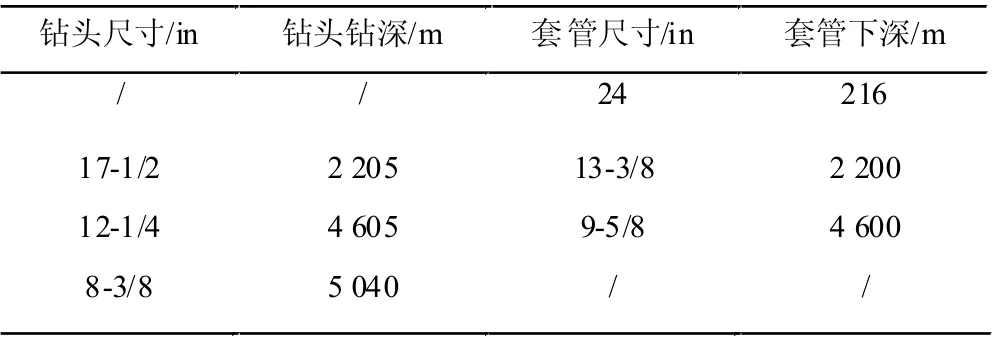
表1 A1s 井身結構設計

3.2 摩阻系數的獲得

摩阻系數和摩擦系數存在差異,但又相互聯系,摩擦系數表征兩個物體之間接觸摩擦產生的阻力系數,是摩擦力和垂直作用力的比值。井筒的摩阻系數是一個廣義的摩擦系數,代表整個井筒內某一段（套管段和裸眼段）的摩擦系數均值。摩阻系數存在時間和空間上的不均一性,時間上隨著井筒內鉆井液性能變化（潤滑性、固相含量）、裸眼段井壁泥餅性質變化而發生變化,空間上因井筒內每一點、每一米表面物理特性不一致,尤其裸眼內砂泥巖層（滲透性導致的泥餅差異、井眼擴大率不一樣）而存在差異。因此推薦采用基于反演的再預測,反演可以是本井目前實際鉆井參數的反演,也可以是周邊相似軌跡、井身結構實際鉆井參數的反演。如圖1,A1s 井反演3 150～3 300 m 時的井筒摩阻系數,可以看出套管內0.29、裸眼內0.38 的情況比較貼近。

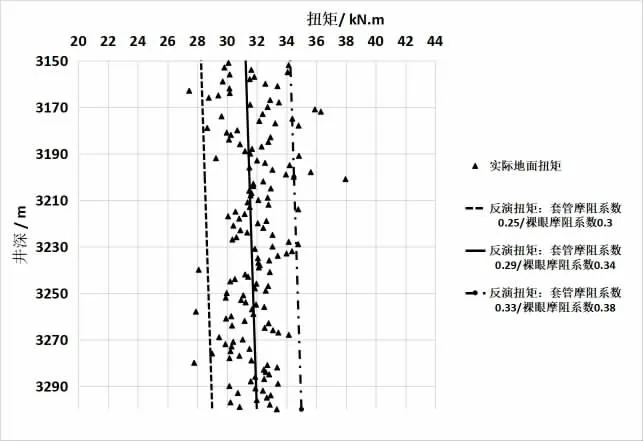
圖1 A1s 井在3 150～3 300 m 的摩阻系數反演

3.3 鉆頭扭摩擦系數的獲得

通過時間軸15 s 導出鉆頭深度和實鉆扭矩的關系散點,根據海上鉆井實際工況：每柱打完倒劃眼2～3遍,因此在二者散點中既有鉆進地面扭矩反應,又有空轉扭矩反應。核心是如何是數據處理中分開實鉆和空轉扭矩,采用的方法是擬合趨勢線法,如圖2 所示,采用線性擬合鉆進扭矩趨勢和空轉扭矩趨勢,獲得線性擬合方程。二者相減獲得實際鉆頭扭矩。

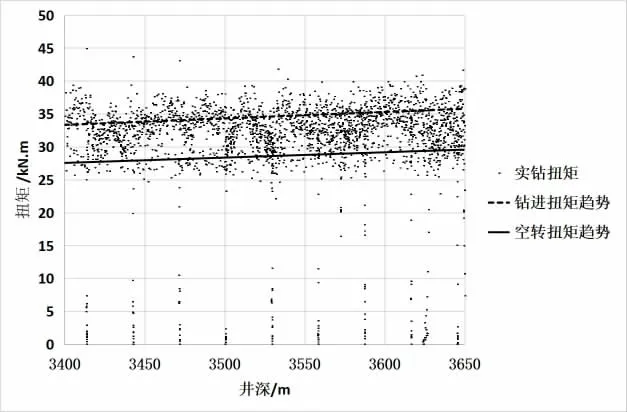
圖2 A1s 井在3 400～3 650 m 的扭矩的分解分析

利用公式（6）以及實鉆鉆壓等參數,計算獲得計算鉆頭扭矩。μ鉆頭取值0.6,擬合度較高。計算誤差率10.37%

3.4 扭矩預測效果

預測是一個不斷反演不斷調整的過程,一口井開鉆的初期采用鄰井的數據反演,鉆進中采用上部或者當前已鉆的反演,預測時既要考慮當前井筒情況,還要參考相鄰下部井段情況,這是一個動態辯證統一的方法。圖3 是A1s 井在整個12.25 in 井段的實際扭矩和預測扭矩的預測情況,可以看出總體預測精度在10%左右。如表2,顯示了整個12-1/4″井段作業過程的井筒摩阻系數反演情況,可以看出,摩阻系數存在各項異性,即便是在同一時間節點,旋轉和上提下放管柱之間存在差異性,因此在工程中建議按照相同操作選擇反演預測。

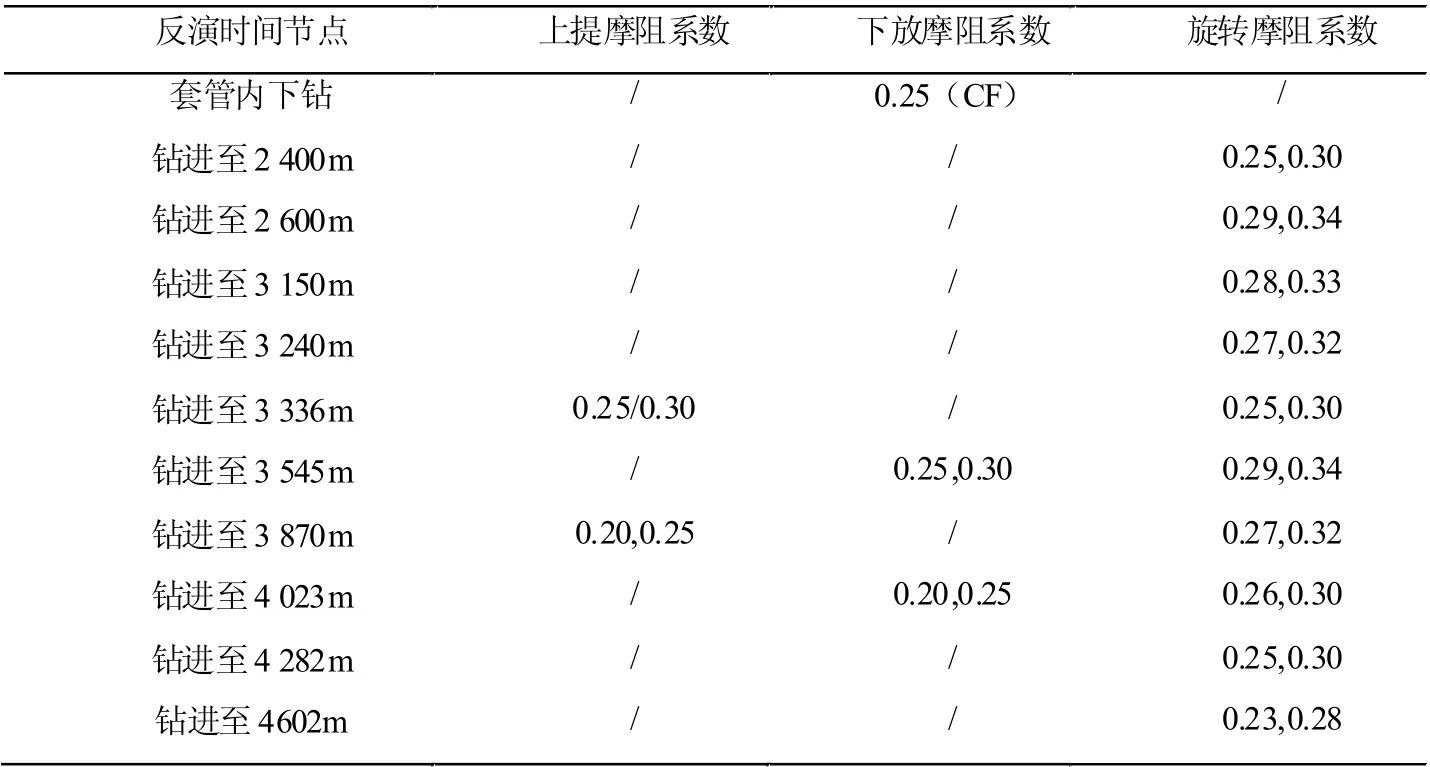
表2 A1s 井在12-1/4″井段的作業過程的井筒摩阻系數反演

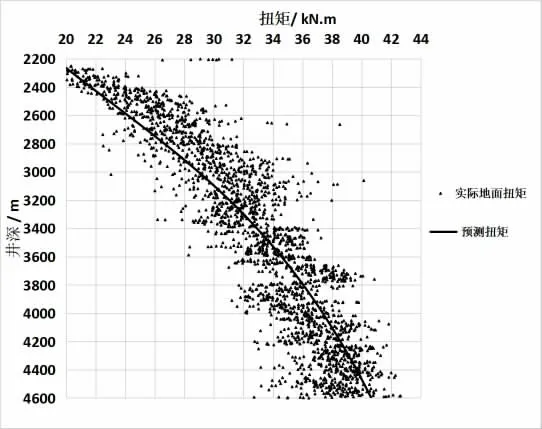
圖3 A1s 井在12-1/4″井段的扭矩預測和實際對比

4 結論

（1） 通過鉆井工程扭矩基本模型的推導,可以看出,隨鉆過程對于摩阻系數的獲得是準確預測扭矩的關鍵。

（2） 摩阻系數不同于狹義的摩擦系數,存在相同條件狀態下的各項異性,也存在時間和空間兩個維度的各向異性。

（3） 通過基于Wellplan的扭矩敏感性和精確技術研究的研究,能夠積極指導現場作業和方案制定,具備廣泛推廣和應用的前景。