基于MGWO-SCN的滾動軸承故障診斷方法*

馮 鈴,張 楚,劉偉渭

（1.四川化工職業技術學院 智能制造學院,四川 瀘州 646000;2.西南大學 人工智能學院,重慶 400715;3.西南交通大學 機械工程學院,四川 成都 610031）

0 引 言

滾動軸承在機械結構中被稱為“工業的關節”,在航空航天、機械制造、風力發電等諸多工業領域中使用廣泛;其運行狀態健康與否對機械設備是否能夠可靠運行有著十分重要的作用[1]。

據相關統計數據表明,旋轉機械的失效案例中,高達45%～55%是由滾動軸承失效引起的[2]。因此,國內外許多學者積極開展了以滾動軸承為典型代表的機械故障診斷研究[3]。

目前,滾動軸承的故障診斷可分為基于模型分析的傳統診斷方法和基于數據驅動的智能診斷方法兩種。其中,基于模型分析的診斷方法是根據第一性原理和軸承失效機制所構建的一種數學或物理模型,以描述軸承的退化過程,因而模型復雜度高且普適性較差。

近年來,隨著人工智能算法和在線監測技術的發展,基于數據驅動的智能診斷方法成為了當前軸承故障診斷領域的研究熱點。

SOUALHI A等人[4]使用自適應神經模糊推理系統估計出了軸承的剩余使用壽命。馬文靜等人[5]基于支持矩陣機（supportmatrixmachine, SMM）數學理論,對基于數據驅動的智能診斷方法進行了改進,提出了一種多分類邊界支持（multi-classification boundary supportmatrixmachine,MBSMM）模型,并將其應用在軸承故障診斷領域中。朱紫悅等人[6]為解決噪聲數據對診斷模型的影響,提出了一種基于ITD-MODMEDA聯合降噪的數據預處理方法,研究結果表明,該方法能夠有效地提高軸承故障診斷模型的準確率。劉飛等人[7]為了提高深度學習訓練效率,提出了一種基于遷移學習和深度殘差網絡的軸承故障診斷模型。DING Xiao-xi等人[8]利用小波變換和相空間重構相結合的方法,重建了振動信號特征,并利用深度卷積網絡實現了軸承故障診斷目的。雖然基于人工智能算法的軸承診斷方法具有很強的普適性,但仍存在著網絡結構難以確定、訓練過程容易陷入局部最優等問題。

為更好地提高模型泛化性能,解決模型結構特異性的問題,越來越多的學者在神經網絡訓練過程中融入隨機學習機制。

1997年,LI J Y等人[9]通過網絡參數隨機生成和輸入層與輸出層直接連接的方式,構建了隨機向量函數連接神經網絡（random vector functional link network, RVFL）。相比于傳統的神經網絡,RVFL訓練效率更高、泛化性能更強。然而,TYUKIN I Y等人[10]的研究表明,RVFL訓練效果易受到隱含層節點數目的影響,若設置不當將導致無法逼近目標函數的最優值。

2017年,WANG Dian-hui等人[11]構建了一種基于不等式約束的監督機制,并利用該機制隨機生成輸入層網絡參數和隱含層節點數,進而提出了一種隨機配置網絡模型。相比于其他神經網絡架構,SCN不僅具有隨機學習的良好泛化特性,并且其隱含層節點數是基于監督機制而逐步生成的,很好地解決了RVFL模型隱含層節點數難以確定的問題。

綜上所述,為提高滾動軸承故障診斷模型的準確率,筆者提出一種基于改進灰狼算法優化隨機配置網絡（MGWO-SCN）的滾動軸承診斷模型。

首先，筆者在SCN中引入L2范數懲罰項;然后,將差分進化策略融入GWO算法中,并將其用來優化SCN的懲罰項系數C;最后,對美國西儲大學的公開數據集進行預處理,選用特征頻率的幅值數據作為MGWO-SCN的特征輸入;為了驗證該模型的有效性,分別從模型診斷性能和算法優化效果的角度,將該模型與BPNN、ELM、SVM以及GWO-SCN、PSO-SCN進行對比仿真測試。

1 正則化隨機配置網絡（SCN）

SCN是一類功能強大的隨機學習模型,與傳統的隨機學習模型相比,其隱含層結構可基于訓練效果自適應生成,因而具有更強的泛化性能[12]。其基本思想是先從一個較小的網絡開始,然后用隨機參數逐步添加新的隱藏節點,直到達到可接受的容差。

對于一個數據集D={（xi,yi）},i=1,…,Ixi∈1×d,yi∈1×m;其中xi表示數據集特征屬性數據,yi表示數據標簽屬性。

L-1個節點的單層前向傳播的神經網絡（SLFN）輸出如下:

（1）

式中:βl=[βl,1,βl,2,…,βl,m]—輸出權重;L—神經網絡層數,為正整數;σI（·）—第l個隱藏神經元的激活函數;wl∈[-v,v]m×d—第l個隱藏神經元的權重;bl∈[-v,v]m×d—第個隱藏神經元的偏置;eL-1=f-fL-1=[eL-1,1,…eL-1,m]—L-1個隱藏層節點的殘差;f—實際標簽類型。

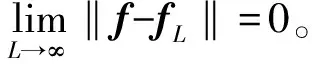
SCN的基本結構圖如圖1所示。

此時,模型根據更新模型輸出權重如下:

（2）

當訓練樣本數量較少時,為避免SCN出現過擬合現象,筆者在模型的目標函數中引入了L2范數懲罰項;同時,最小化經驗風險和結構風險,以此來提高網絡的泛化性能。

此時,SCN的目標函數做出如下改進:

（3）

式中:C—模型的懲罰項權重系數。

根據最小二乘法輸出權值定義為:

β*=（GGT+λI）-1GT

（4）

式中:G=σ（wT·x+b）—隱含層輸出。

2 改進灰狼算法優化（MGWO）

2.1 灰狼算法優化（GWO）

元啟發式優化算法是一種處理實際優化問題的常用方法,其通過模擬自然對未知世界的探索,實現全局尋優[13]。PSO算法是一種比較成熟的優化算法,由于其參數少、收斂速度快,在工程問題上受到廣泛應用[1]。

但PSO的全局搜索能力較差,易陷入局部最優,因此,筆者采用了一種具有良好探測能力的GWO。GWO通過模擬狼群的等級制度和狩獵行為實現全局尋優[2]。

狼群等級排列結構圖如圖2所示。

圖2中,筆者根據灰狼狩獵的能力將群體進行劃分,最終產生3頭能力最強的灰狼個體,依次記作α、β和δ。

個體位置更新通過模擬狼群捕獵食物實現,其數學模型如下[3]:

（5）

（6）

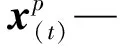
系數和的計算如下:

A=a×（2×r1-1）

（7）

C=2×r2

（8）

隨著迭代次數的增大,a的數值將從2線性減少到0,r1和r2表示在區間[0,1]上的隨機數。

當頭狼發現獵物的位置時,其他狼在頭狼的帶領下朝著獵物移動,其數學表達式為:

Dα=|C×xα-x（t）|
Dβ=|C×xβ-x（t）|
Dδ=|C×xδ-x（t）|

（9）

式中:xα—個體α的當前位置;xβ—個體β的當前位置;xδ—個體δ的當前位置。

基于狼群的捕獵思想,狼群其他個體分別向個體α、β和δ進行逼近,最終獲取更新位置。

其數學模型為:

（10）

式中:x1,x2,x3—分別表示當前個體逼近α、β和δ位置的過程向量。

考慮了3種位置逼近方向下的個體最終更新位置如下:

（11）

2.2 改進灰狼算法優化（MGWO）

GWO算法是首先根據個體適應度值確定α狼、β狼和δ狼的地位,接著將其他個體按照線性方向逼近3只頭狼位置,進而實現全局最優解的探索。

然而,該機制只會讓個體無限趨近于α狼、β狼和δ狼的個體位置,且隨著更新系數A的衰減,算法會陷入局部最優[4]。因此,筆者在α狼、β狼和δ狼之間融入差分進化機制,使得個體位置更新過程中產生更加豐富的個體位置[5]。

其中,個體變異因子向量公式如下:

v（t+1）=xα+W·（xβ-xδ）

（12）

式中:v（t+1）—變異因子;W—差分變異權重系數。

完成個體變異操作后,基于差分進化的思想,要對灰狼個體進行交叉操作。

灰狼個體交叉的數學模型如下:

（13）

（14）

筆者選用模型預測值與真實值偏差的二范數作為MGWO適應度函數,即:

f（x）=‖Y-M（x）‖

（15）

式中:Y—數據真實標簽;M（x）—模型在參數x的預測輸出值。

此處的MGWO算法的流程圖如圖3所示。

3 基于MGWO-SCN的軸承診斷模型

3.1 數據預處理

此處的實驗數據采用來自美國凱斯西儲大學（CWRU）軸承振動信號數據集,以此來驗證MGWO-SCN模型的性能[6]。

實驗平臺由3部分組成,分別為1.5 kW的電動機、功率測試計和扭矩傳感器,其結構如圖4所示。

信號由驅動端傳感器采集,采樣率為48 kHz,電機負載為0時,軸承轉速1 797 r/min。故障軸承被放置在驅動端（driveend, DE）和風扇端（fan end, FE）,利用電火花人工添加故障的方式在軸承滾動體的外圈、內圈上分別加工了0.17 mm、0.35 mm、0.53 mm的3種不同尺寸故障。

筆者對不同運行狀態下的各部位振動信號進行了傅里葉變換,以獲取頻譜圖。

不同運行狀態下的各部位振動信號頻譜圖,如圖5所示。

在圖5中,驅動端和風扇端振動信號的幅頻曲線在不同軸承運行條件下均存在著差異,因此,筆者將不同部位、不同工況下振動信號的特征頻譜成分作為數據集的特征屬性。

12種軸承故障類型選擇的特征頻段篩選結果,如表1所示。

筆者以被測軸承旋轉一圈,傳感器所采集的振動信號作為一組數據,則該樣本數據的大小與傳感器采樣頻率和轉速相關,其計算公式如下[22]:

（16）

式中:nc—樣本點數;m—轉速;fs—采樣頻率。

經過計算可知,旋轉一圈后軸承傳感器采集1 600個點;接著,筆者對軸承旋轉一圈產生的振動信號進行幅頻分析,并根據表1依次選取驅動端和風扇端[23]的特征幅頻,作為該模型的輸入數據。

筆者通過上述方法構建軸承12種運行狀態的樣本空間,并將樣本的70%作為訓練集,20%作為測試集,10%作為驗證集。

各類樣本數目,即軸承振動信號分析數據集樣本數量,如表2所示。

表2 軸承振動信號分析數據集樣本數量

3.2 MGWO-SCN模型

MGWO-SCN軸承故障診斷流程圖如圖6所示。

筆者利用MGWO對SCN模型的懲罰權重系數C進行優化,在搜索空間中,不斷探索最優的系數值,并根據適應度值大小確定全局最優位置。

針對灰狼優化算法容易陷入局部最優、收斂速度較慢的問題,筆者提出了將差分進化機制融入到GWO中的改進策略[7]。

首先,筆者根據適應度計算的結果,將每一代灰狼種群中適應度值最優的前3個個體直接視為新的α狼、β狼和δ狼;其次,為增加更新過程中種群的多樣性,將差分進化機制融入到GWO算法中,有效地彌補了GWO迭代過程中個體位置易陷入局部最優解的缺陷。

筆者將MGWO的種群個體數設置為50、最大迭代次數設為50、交叉概率K設為0.5,個體搜索空間為[0,200]。

此外,為了避免SCN出現過擬合,筆者在網絡中加入正則化懲罰項,以彌補僅依據最小化經驗風險導致的過擬合現象。

4 模型仿真及結果分析

筆者對MGWO-SCN進行30次重復實驗,12種軸承運行狀態的測試集準確率及標準差,如表3所示。

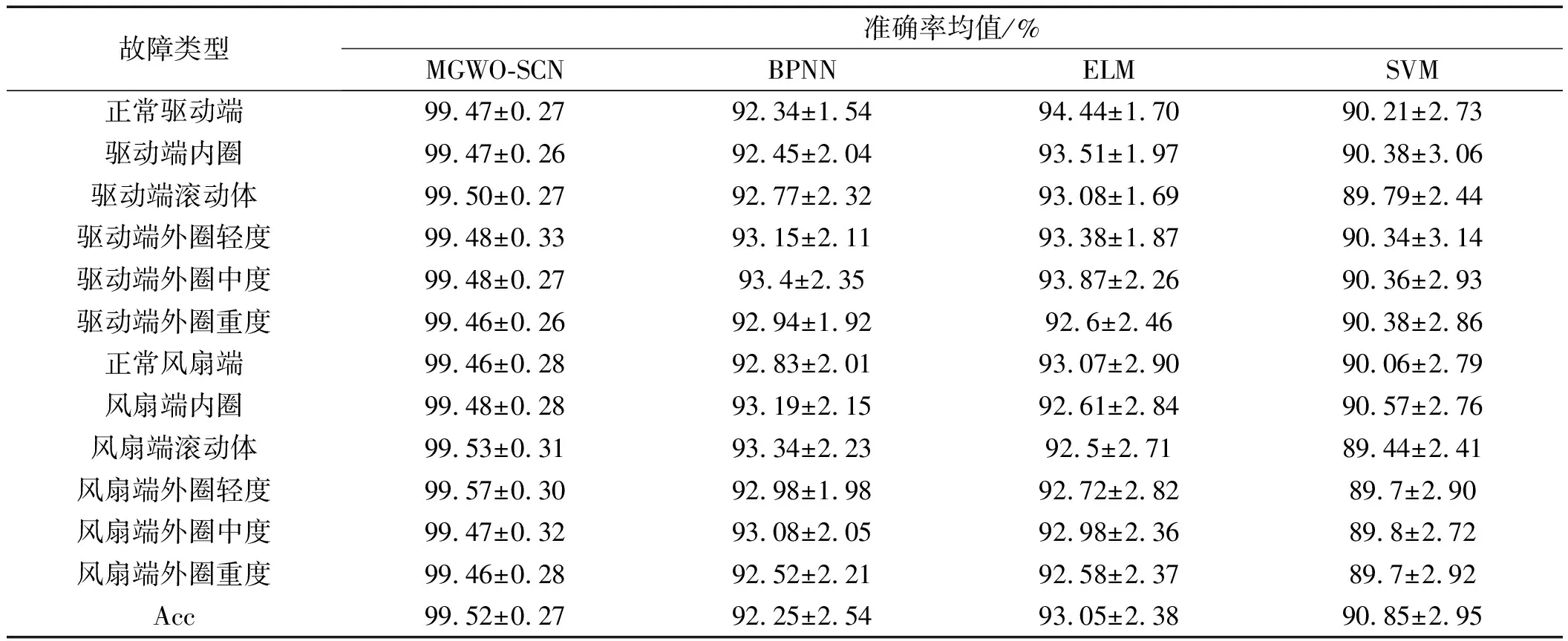
表3 MGWO-SCN、BPNN、ELM、SVM下的準確率和標準差

仿真結果表明:對于正常的軸承樣本,驅動端和風扇端識別準確率分別為99.47%、99.46%,30次重復實驗結果的準確率標準差分別為0.27%、0.28%。

此外,為了驗證筆者所提方法的優越性,筆者分別選取BPNN、ELM、SVM,按照相同的思路進行30次重復實驗,同樣選取其識別準確率均值與標準差進行對比。

由表3可以看出:BPNN、ELM、SVM這3種分類算法的準確率均值均不及MGWO-SCN,其中,SVM對12種軸承故障的識別準確率最低,軸承風扇端內圈故障的準確率僅為90.57%,比MGWO-SCN方法低了8.89%。

為了驗證改進的GWO策略在模型優化問題上的優越性,筆者分別對比了MGWO、GWO和PSO在優化該模型上的性能。

基于控制變量法的思想,將GWO和PSO的個體數目和迭代次數均設置為50,搜索空間為[0,200]。其中,PSO的粒子飛行速度范圍為[-5,5]。

在優化SCN模型過程中,采用3種不同優化算法得到的適應度收斂曲線圖,如圖7所示。

圖7曲線顯示:GWO-SCN和PSO-SCN適應度曲線過早收斂,而MGWO-SCN在迭代26次后才逐步收斂,具有跳出局部最優的能力;隨著迭代次數的增加,MGWO-SCN的適應度逐漸收斂到0.5以下,其余優化算法適應度收斂值均高于0.5。

基于上述數據分析,驗證了筆者提出的改進策略能夠有效地提高GWO的全局搜索性能,并且相比于PSO和GWO,MGWO在優化該模型問題上具有較強的搜索能力[24]。

MGWO-SCN輸出結果圖如圖8所示。

GWO-SCN輸出結果圖如圖9所示。

PSO-SCN輸出結果圖如圖10所示。

通過對比可以發現:MGWO-SCN模型診斷結果在測試集中僅存在2例識別錯誤樣本,而其他2種模型存在大量識別錯誤樣本。

MGWO、GWO和PSO優化SCN模型在不同故障類型診斷準確率的統計數據表,如表4所示。

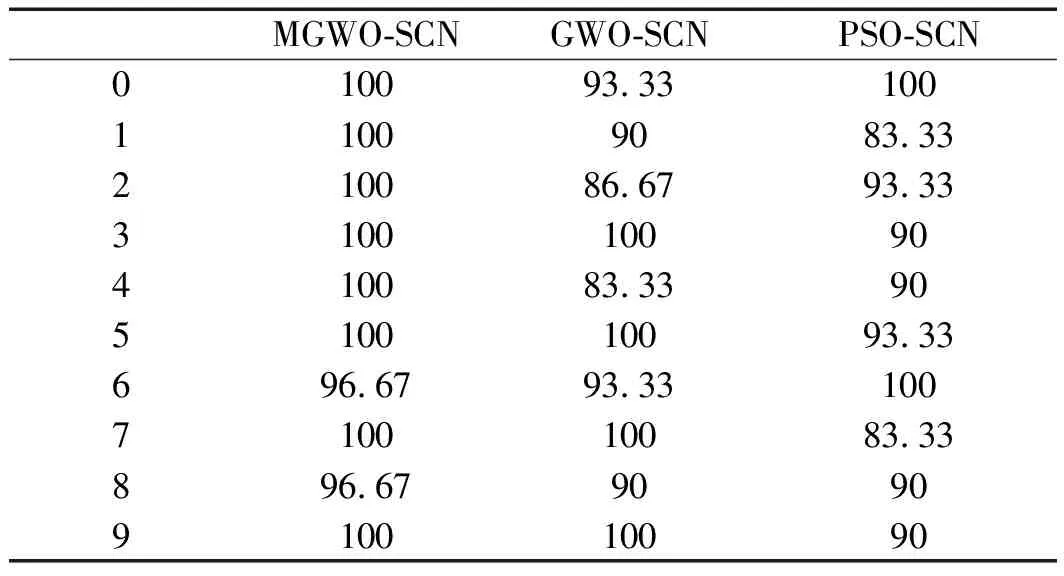
表4 不同優化算法各類故障診斷準確率（%）

表4數據顯示:相比于GWO-SCN和PSO-SCN,MGWO-SCN模型準確率分別提高了6.11%和7.5%,進一步驗證了該模型具有良好的魯棒性,MGWO的改進策略對該模型具有明顯提升性能的作用。

5 結束語

針對非線性、不平穩的滾動軸承振動信號,筆者利用傅里葉變換構建了頻域特征下的軸承振動數據集;為了提高診斷模型的準確率,筆者從算法角度對模型進行了改進和研究;針對優化算法易陷入局部最優的問題,筆者將差分進化機制融入到GWO搜索策略中,構建了MGWO算法;為避免模型出現過擬合的情況,在SCN中加入了正則化懲罰項,以減少模型結構風險對網絡泛化能力的影響。

研究結果表明:

（1）采用基于MGWO-SCN的滾動軸承故障診斷方法,可以準確地識別12種軸承運行狀態,準確率最高為99.57%,在分類精度上優于BPNN、ELM、SVM方法;

（2）相比于PSO和GWO算法,MGWO在優化該模型參數上具有較強的全局搜索能力,診斷準確率分別提高了6.11%和7.5%。

考慮到軸承健康狀態在機械結構中起著至關重要的作用,基于振動信號數據預測軸承狀態發展趨勢將是筆者后續研究工作的重點。