模糊支持張量訓練機及其在滾動軸承故障診斷中的應用*
王勁鋒,薛玉石,山春鳳
(1.江蘇聯合職業技術學院 揚州技師分院,江蘇 揚州 225000;2.國機精工股份有限公司,河南 鄭州 450142;3.洛陽軸承研究所有限公司,河南 洛陽 471039)
0 引 言
目前,滾動軸承在工業領域中得到了廣泛應用。在旋轉機械中,滾動軸承更是最常見的零部件之一。然而,由于滾動軸承惡劣的工作環境,使其易出現疲勞損傷,從而降低設備的可靠性,并可能由此引發事故。因此,國內外相關學者針對滾動軸承故障診斷已經展開了大量的研究[1]。
作為故障診斷最常用的方式之一,基于機器學習的狀態評估方法被廣泛應用于滾動軸承的故障診斷領域。常用的狀態評估分類方法包括:極限學習機(extreme learning machine,ELM)[2]、卷積神經網絡(convolutional neural network,CNN)[3]、寬度學習系統(broad learning system,BLS)[4]和支持向量機(SVM)[5,6]等。學者們采用上述方法,并利用故障特征之間的相互關系,建立了故障預測模型。預測模型在狀態評估時展示了優越的分類性能。
然而,上述方法存在分類效率低、線性不可分等問題。
針對上述問題,相關學者開展了一系列的研究。舒星等人[7]提出了一種改進最小二乘支持向量機,并對其參數進行了尋優,采用該方法實現了鋰離子電池容量的預測。孫禾等人[8]提出了改進孿生支持向量機,并通過求解對偶問題的方式提高了其算法的效率,采用該方法完成了對齒廓圖像邊緣失真分類。劉敬等人[9]提出了單分類支持向量機,并據此分析了不同故障特征的數據關聯性,提高了網絡異常檢測準確率。
同時,采用上述方法還有效地解決了分類效率低、線性不可分等問題[10]。
然而,大多傳統的智能狀態評估方法都是基于特征向量作為輸入數據,難以有效地獲取原始故障振動信號中包含的狀態信息,進而影響其故障診斷的效果。此外,在實際工程中,拾取到的振動信號往往不是由單源傳感器采集,而是由多源傳感器共同采集獲得。
鑒于此,相關學者通過構建高階張量作為輸入,提出了高階支持張量分類模型。比如,HAO等人[11]提出了支持高階張量機(support high-order tensor machine,SHTM),實現了對高階數據的準確分類。DENG等人[12]提出了支持Tucker機(support tucker machines,STuMs),并分析了高維數據的關聯性,提高了其分類性能,解決了多源信號的診斷問題。
但是,上述方法在建模過程中沒有考慮樣本不平衡狀況對模型產生的影響,使得建立的模型容易偏向與樣本較多的一類,這使得所建立的模型還不是準確的預測模型[13,14]。
為了實現不平衡樣本情況下的精確建模與分類,筆者基于張量分解理論提出一種基于模糊支持張量訓練機(FSTTM)的狀態評估方法。在FSTTM中,為了能夠采用高階張量數據進行訓練,筆者引入張量訓練(TT)[15]分解方法進行模型構建,并采用基于TT的核函數解決非線性分類問題;同時,FSTTM在目標函數中引入模糊因子,通過計算不同樣本相對于所有樣本的距離,得到每個樣本對預測模型施加的權重,從而提高模型在不平衡樣本下的分類性能。
綜上所述,在張量分解的基礎上,筆者提出一種FSTTM算法。首先,構建張量樣本,以充分獲取高階張量樣本的特征信息;然后,利用基于TT核函數建立線性不可分下的預測模型,實現非線性數據的分類問題;接著,設計模糊因子,以平衡不同數目的樣本對建模的影響,實現樣本不平衡數據的有效分類;最后,通過在滾動軸承故障數據集上進行實驗分析,驗證FSTTM方法在樣本不平衡情況下的故障診斷性能。
1 模糊支持張量訓練機及其理論
1.1 支持向量機
支持向量機(SVM)是一種經典的二分類機器學習方法[16,17],其訓練集定義為:S={(xi,yi)|i=1,2,…,n}(xi∈I1—向量樣本,yi∈{-1,1}—類別標簽)。
為了對數據集S進行訓練,并得到分類模型,其目標函數為:
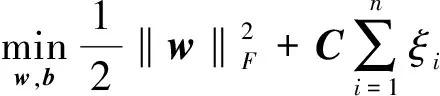
(1)
式中:w—訓練得到的權重向量;b—閾值;ξi,i=1,2,…,n—松弛變量。
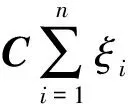
1.2 模糊支持張量訓練機
為了直接對基于張量的多源故障振動信號進行分類,并在訓練數據不平衡的情況下提高其分類性能,筆者提出了一種FSTTM方法。
筆者給定訓練樣本集S={(Xi,yi)|i=1,2,…,n}(Xi∈I1×I2×…×IN—N階張量樣本,yi∈{-1,1}—類別標簽),通過為每個樣本分配不同的模糊因子,建立目標函數,即;
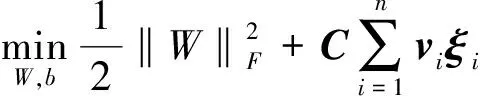
(2)
式中:W—權重張量;b—偏量;ξi—松弛變量;vi—任意樣本模糊因子;C—損失懲罰參數。
利用拉格朗日乘子法,可以得到目標函數(2)的對偶問題為:
(3)
為了充分挖掘和利用張量數據中固有的結構信息,筆者引入一種有效的TT分解方法。
對于張量數據Xi和Xj,TT分解定義為:
(4)
式中:G(n)∈Rn-1×In×Rn(n=1,…,N)—3階張量,稱為TT核;R0,…,RN—TT秩,且滿足張量因子,且有
兩個張量的內積可以表示為:
〈Xi,Xj〉=
(5)
將式(5)代入式(3)中,可得:
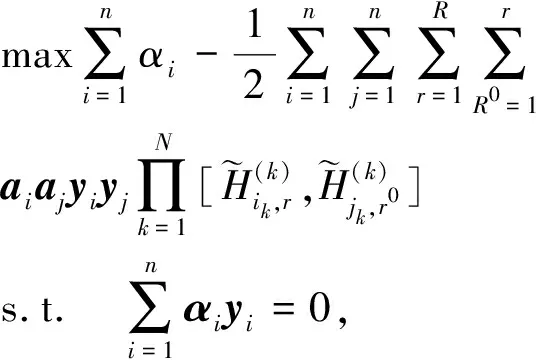
(6)
對于非線性分類問題,張量X可以利用式(7)映射到張量積再生核希爾伯特空間。
映射張量表示為φ(X):
φ:X→φ(X)∈F1×F2×…Fr
(7)
因此,式(6)可以轉化為:
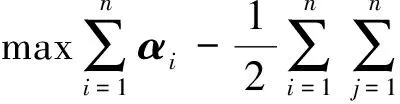
(8)
在式(8)中,2個映射張量〈φ(Xi),φ(Xj)〉的內積定義為κ(Xi,Xj)。
根據TT張量分解,可得:
〈φ(Xi),φ(Xj)〉=κ(Xi,Xj)
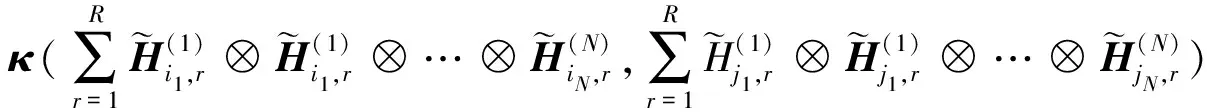

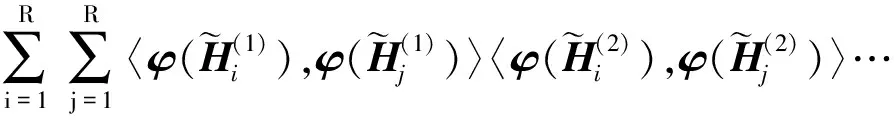
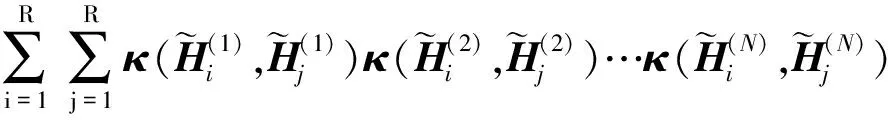
(9)
高斯徑向基核函數為:
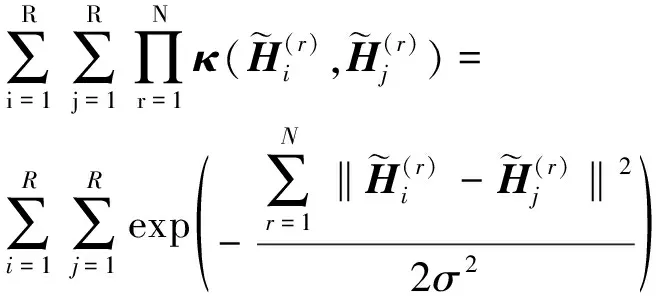
(10)
式中:σ—核參數。
通過式(10),式(9)可以轉化為(即對偶問題):
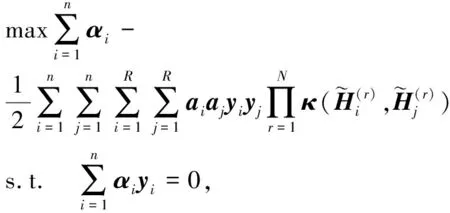
(11)
最后,筆者利用所得參數構造決策方程為:
(12)
2 實驗及結果分析
2.1 錐齒輪-滾動軸承故障模擬實驗
為了驗證FSTTM方法的可行性,筆者采用錐齒輪-滾動軸承振動信號數據集進行實驗測試。
錐齒輪-滾動軸承故障模擬實驗臺如圖1所示。
筆者利用該實驗臺采集滾動軸承在不同狀態下的振動信號,并利用不同狀態的振動信號建立數據集,如表1所示。
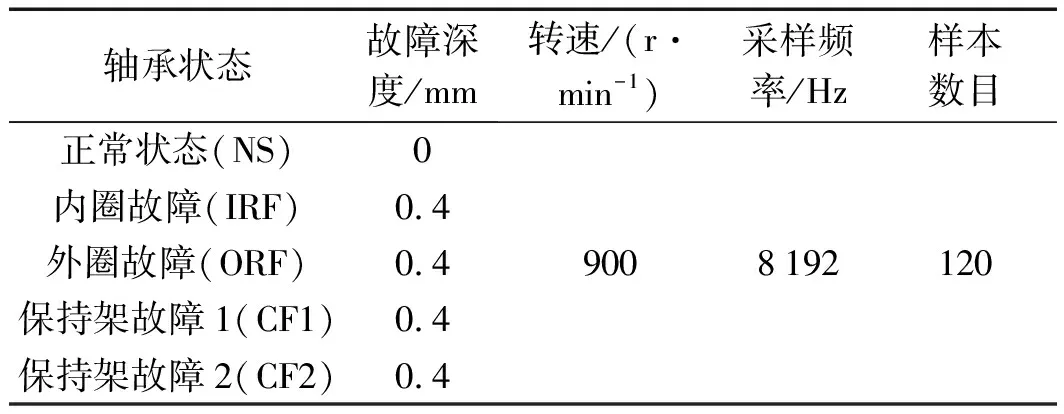
表1 滾動軸承的狀態與實驗樣本的相關信息
表1展示了滾動軸承的不同狀態信息以及后續驗證實驗選取樣本的相關信息。實驗中,筆者選擇SVM、TSVM、STuMs和SHTM方法作為對比方法,以Accuracy和F1-score作為不同方法的對比衡量指標。
為了驗證FSTTM方法在樣本不平衡情況下的故障診斷性能,筆者擬采用該方法進行多組樣本不平衡率下的分類實驗。
由于篇幅限制,筆者采用差位選擇法設定不平衡率,即樣本不平衡率設置為2、4和6(不平衡率為6時,極度不平衡)。當不平衡率為1時,代表正類樣本數目和負類樣本數目相等(等同于樣本平衡);當不平衡率為2時,代表正類樣本數目和負類樣本數目的比值為2,此時樣本出現不平衡現象。以此類推,相繼選擇不平衡率為2、4和6時,完成樣本不平衡分類實驗。
樣本不平衡率設置結果如表2所示。
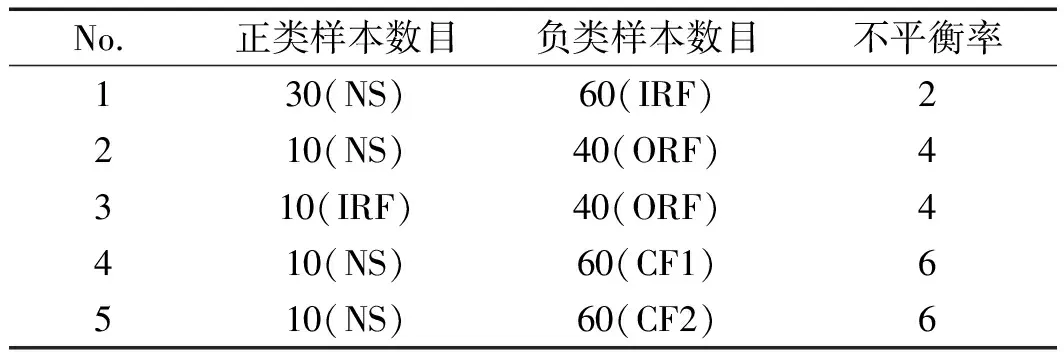
表2 不同的樣本不平衡率
為了構造張量樣本,筆者從三向傳感器采集的3個方向(X、Y和Z)的振動信號中,分別選擇160個樣本構造樣本集,每個樣本包含1 024個采樣點;然后,使用辛幾何相似變換,對每個方向的樣本進行預處理,得到尺寸為32×32的辛幾何系數矩陣。
為了構造不同狀態的張量樣本,筆者將3個方向的辛幾何系數矩陣分別作為張量的水平切片,得到尺寸為32×32×3的張量樣本,并使用不同狀態的滾動軸承振動信號構建3階張量樣本,如圖2所示。
筆者根據表2中的不平衡條件選擇訓練樣本,并從每個狀態下選擇60個樣本構建測試樣本集。為了避免偶然性的問題,筆者采用五折交叉驗證方法對3種方法進行實驗。
在不同不平衡條件下,采用3種方法得到的實驗結果如表3和表4所示。

表3 不同方法的分類結果的Accuracy(%)
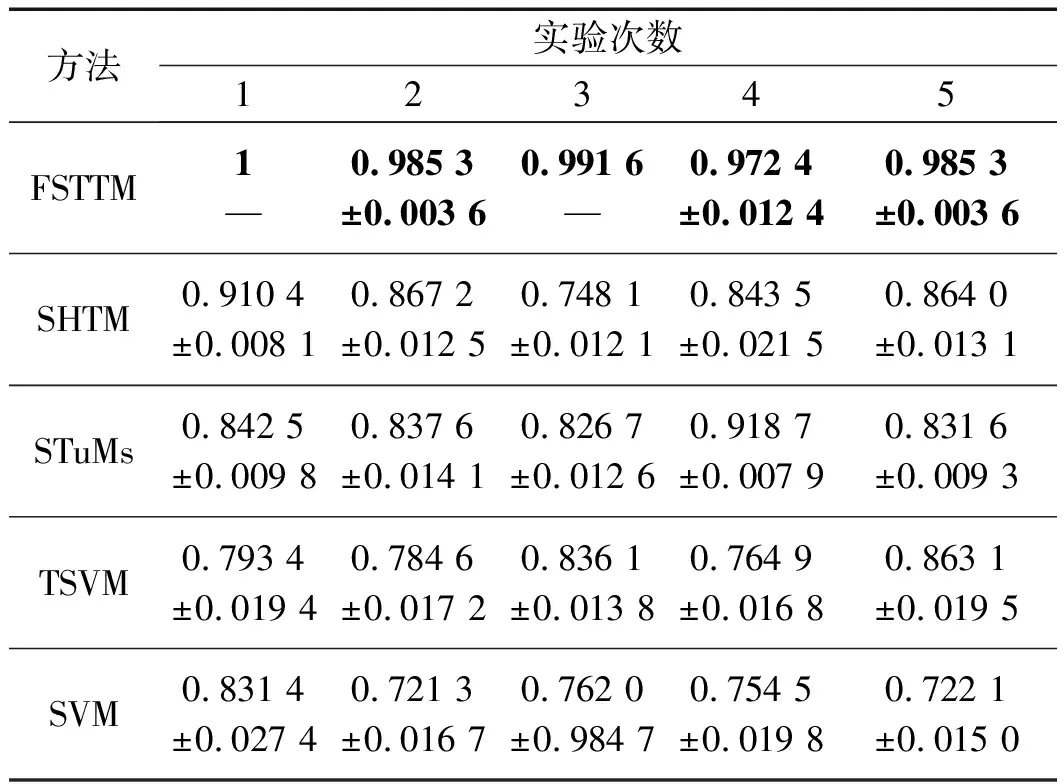
表4 不同方法的分類結果的F1-score
從表(3,4)可以看出:
FSTTM在各種條件下識別率均為最高。在條件1下,其分類正確率為100%,而SVM、TSVM、STuMs和SHTM僅為81.21%、80.32%、85.35%和90.32%;
隨著樣本不平衡率的增加,5種方法的識別率也在改變,但FSTTM的識別率均保持在97%以上。這是因為FSTTM在建模中引入模糊因子,能夠對不平衡樣本進行加權,提高了在不平衡條件下模型的擬合程度;
SVM和TSVM依賴向量作為輸入,無法直接利用高階張量數據的結構信息,使得建模時破壞了張量特有的結構,導致其分類性能低;
SHTM和STuMs盡管能夠直接利用高階張量數據進行建模,但沒有考慮不平衡問題對分類產生的影響,因而制約了其分類性能。
2.2 常規滾動軸承故障模擬實驗
為了再次驗證FSTTM方法的有效性,筆者擬選擇常規滾動軸承故障模擬實驗臺進行實驗和數據分析。
常規滾動軸承故障模擬實驗臺如圖3所示。
不同狀態下的滾動軸承相關信息如表5所示。
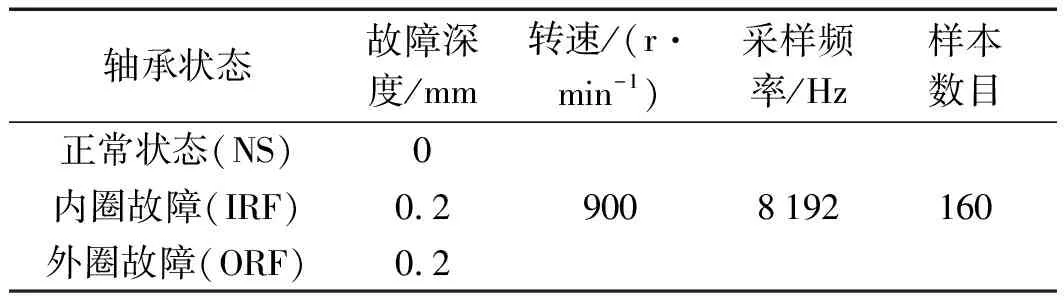
表5 滾動軸承的狀態與實驗樣本的相關信息
同時,為了驗證FSTTM方法在樣本不平衡工況下的分類性能,筆者構建不同的樣本不平衡率,并以此為依據選擇訓練樣本。
筆者構建的樣本不平衡率如表6所示。
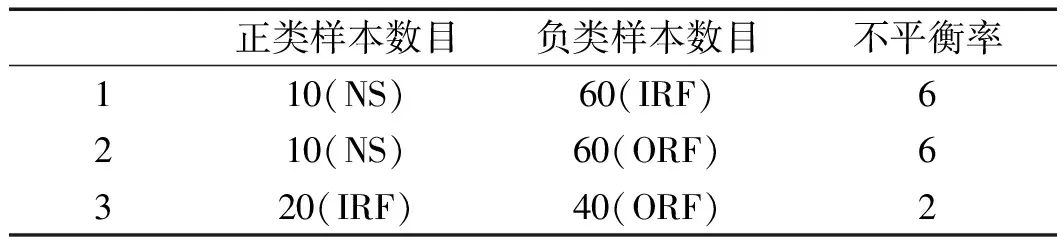
表6 不同的樣本不平衡率
首先,筆者對采集的振動信號構建張量空間。
不同狀態振動信號構造的張量樣本如圖4所示。
然后,筆者利用構建的張量數據,對5種方法進行五折交叉驗證實驗。采用不同方法得到的分類實驗結果(accuracy)如表7所示。
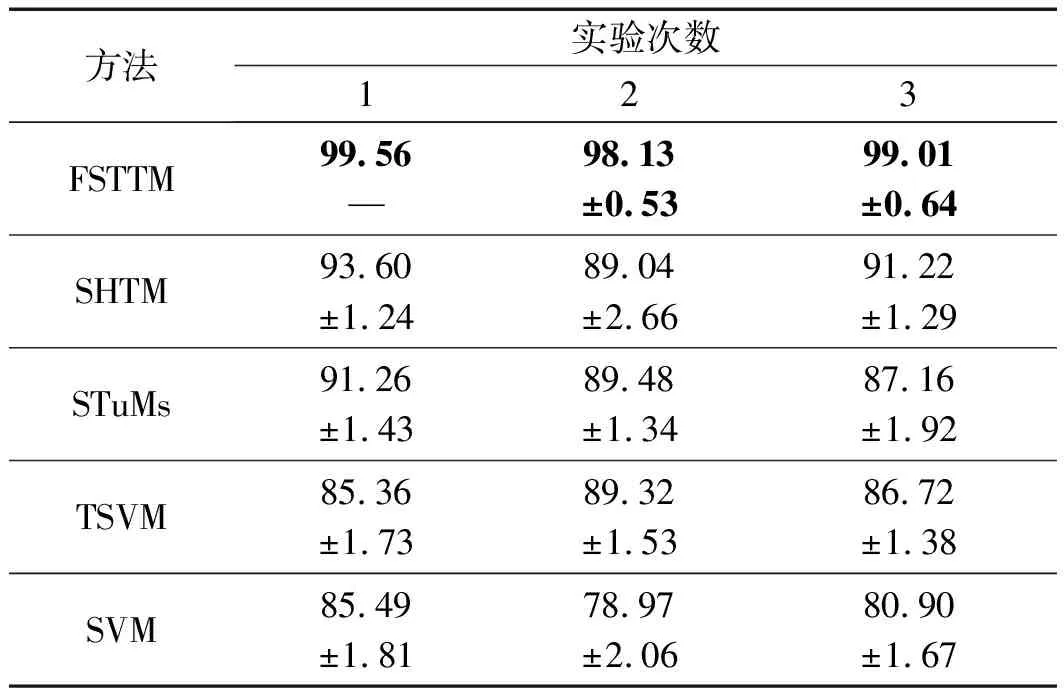
表7 不同方法的分類結果(accuracy)(%)
得到的分類實驗結果(F1-score)如表8所示。
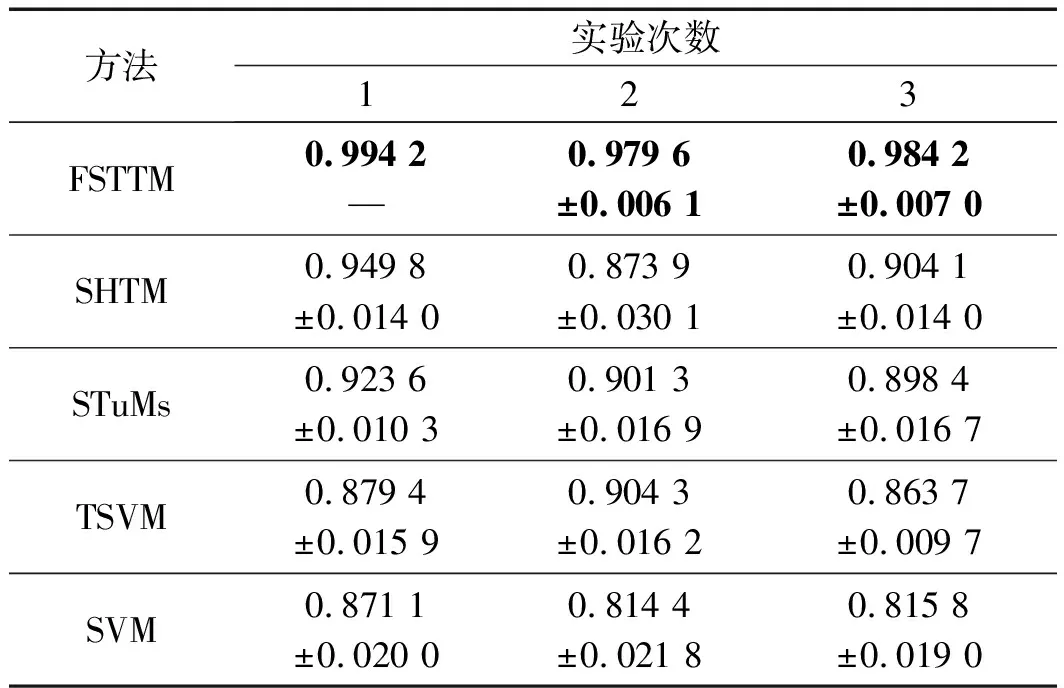
表8 不同方法的分類結果(F1-score)
從表(7,8)可以看出:在不同的條件下,FSTTM的分類正確率均最高。在不平衡條件3下,盡管不平衡度僅為2,FSTTM的分類正確率仍然達到99.01%,此時SVM、TSVM、STuMs和SHTM的分類正確率分別為80.90%、85.36%、91.26%和91.22%。究其原因在于FSTTM采用基于TT的核函數對原始數據進行映射,提高了張量數據的可分性;
同時,FSTTM模型中采用模糊因子,能夠對不同樣本施加不同的權重,弱化不平衡樣本對建模產生的影響。
3 結束語
筆者基于張量分解理論提出了一種基于FSTTM的滾動軸承故障診斷方法。首先,通過構造高階張量,實現了原始信號結構信息的充分利用;然后,基于TT核函數建立了非線性預測模型,以完成復雜數據的有效分割;接著,引入了模糊因子,平衡不同樣本對模型的貢獻度,解決了樣本不平衡數據分類的問題;最后,將FSTTM應用于滾動軸承故障診斷中。
研究結論如下:
(1)FSTTM能夠對原始故障振動信號構建高階張量,在其模型中引入一種TT方法,對張量數據進行了預處理,實現了對高階張量結構信息的提取與分析,完成了非線性數據的分類問題;
(2)在FSTTM中引入了模糊因子,通過對不同樣本施加不同的權重,均衡模型對不同類別樣本的傾向性,進而提高了模型在不平衡樣本下的分類性能;
(3)通過對2個滾動軸承故障診斷實驗結果的分析,FSTTM方法能夠有效地利用高階張量數據進行分類,且在不同的不平衡條件下均能實現優越的診斷效果。
雖然FSTTM方法實現了優異的診斷結果,但依然存在其他可以改進的地方,如張量樣本構建、參數尋優等。
因此,在今后的研究工作中,筆者將針對張量樣本構建問題進行研究,以進一步提高不平衡情況下該方法的故障診斷性能和效率。

