時(shí)滯位置反饋對一類梳齒型微陀螺振動(dòng)系統(tǒng)復(fù)雜動(dòng)力學(xué)行為的控制
尚慧琳, 蔣慧敏, 秦 波
(上海應(yīng)用技術(shù)大學(xué) 機(jī)械工程學(xué)院,上海 201418)
微陀螺以其尺寸小、精度高等特點(diǎn),越來越受到人們的關(guān)注,在汽車導(dǎo)航、移動(dòng)應(yīng)用以及航空航天等領(lǐng)域被廣泛應(yīng)用[1-2]。在應(yīng)用的過程中,發(fā)現(xiàn)其非線性因素的對微陀螺的靈敏度、穩(wěn)定性造成極大的影響,為此,微陀螺的非線性動(dòng)力學(xué)問題引起了國內(nèi)外學(xué)者廣泛關(guān)注[3]。張琪昌等[4]探究了雙極板微諧振器振動(dòng)特性與環(huán)境壓力以及立方非線性靜電剛度的關(guān)系,發(fā)現(xiàn)三次非線性靜電剛度會使微機(jī)械諧振器表現(xiàn)出或軟或硬的非線性特性。Zegadlo等[5]探究了具有線性增益和非線性吸收的兩個(gè)耦合環(huán)形諧振器系統(tǒng)的混沌動(dòng)力學(xué)行為。高嶸等[6]考慮微諧振器空氣阻尼力的非線性因素,得到非線性阻尼力的平板振幅非常接近試驗(yàn)值,驗(yàn)證了非線性阻尼力的存在。Mojahedi等[7]數(shù)值模擬發(fā)現(xiàn)非線性參數(shù)對微機(jī)械陀螺系統(tǒng)吸合不穩(wěn)定和偏轉(zhuǎn)的影響。郝燕玲等[8]研究了多自由度微陀螺的結(jié)構(gòu)參數(shù)對其性能的影響,為多自由度陀螺結(jié)構(gòu)參數(shù)的選取指明了方向。Zhang等[9-10]用數(shù)值模擬研究了驅(qū)動(dòng)電壓和檢測電壓對微陀螺周期運(yùn)動(dòng)及其分岔的影響,并考慮了系統(tǒng)的吸合效應(yīng),結(jié)果表明,在適當(dāng)?shù)臋z測電壓范圍內(nèi),系統(tǒng)可能具有最大的機(jī)械靈敏度和最小的非線性。尚慧琳等[11]利用分岔理論和數(shù)值模擬揭示系統(tǒng)參數(shù)對一類切向梳齒驅(qū)動(dòng)微陀螺驅(qū)動(dòng)和檢測模態(tài)振幅影響,結(jié)果表明,激勵(lì)頻率的變化容易引起微陀螺振動(dòng)系統(tǒng)的多穩(wěn)態(tài)解和概周期等復(fù)雜動(dòng)力學(xué)行為。
為了保障微器件的正常工作,應(yīng)對其振動(dòng)跳躍、吸合不穩(wěn)定和混沌等復(fù)雜動(dòng)力學(xué)行為實(shí)施有效控制。對于微機(jī)電系統(tǒng)來說,在其微小結(jié)構(gòu)上直接施加主動(dòng)控制對本身結(jié)構(gòu)易產(chǎn)生極大影響,是不太可行的。因此,大多數(shù)的控制都是在驅(qū)動(dòng)電路上施加。Li等[12]通過在振動(dòng)式微回轉(zhuǎn)儀的矩形束流四個(gè)表面上增加壓電薄膜,提高壓電交流在穩(wěn)定區(qū)域幅值,使振動(dòng)微梁陀螺儀具有較好的靈敏度。郝淑英等[13]運(yùn)用多尺度法和數(shù)值計(jì)算相結(jié)合方法對微梁幾何非線性設(shè)計(jì)和調(diào)控驅(qū)動(dòng)剛度非線性導(dǎo)致的硬化特性來平衡靜電力帶來的軟化特性,避免了系統(tǒng)頻率失穩(wěn)和振幅跳躍現(xiàn)象。李偉雄[14]探究時(shí)滯速度、位移反饋控制對含剛度非線性的雙驅(qū)動(dòng)雙檢測四自由度微陀螺動(dòng)態(tài)性能的控制作用。李欣業(yè)等[15]提出對敏感質(zhì)量施加時(shí)滯反饋來抑制一類簡諧激勵(lì)兩自由度微陀螺振動(dòng)系統(tǒng)的雙穩(wěn)態(tài)現(xiàn)象多數(shù)控制方法。Luo等[16]研究了微機(jī)電系統(tǒng)(micro electro mechanical systems, MEMS)微諧振器的混沌力學(xué),提出一種自適應(yīng)控制方法抑制系統(tǒng)在主諧振頻率附近混沌振蕩。Zhang等[17]運(yùn)用數(shù)值模擬靜電驅(qū)動(dòng)MEMS諧振器在隨機(jī)擾動(dòng)下的非線性動(dòng)態(tài)和混沌行為,通過Melnikov函數(shù)分析,發(fā)現(xiàn)隨機(jī)噪聲會影響系統(tǒng)非線性特性,增加噪聲強(qiáng)度會擴(kuò)大系統(tǒng)產(chǎn)生混沌的區(qū)域。Li等[18]運(yùn)用Lyapunov穩(wěn)定性和自適應(yīng)控制技術(shù),得到了具有不確定性和擾動(dòng)的分?jǐn)?shù)階混沌系統(tǒng)網(wǎng)絡(luò)化同步的充分條件,通過理論分析和數(shù)值仿真提出的網(wǎng)絡(luò)同步策略能在不影響同步性能的前提下有效地減少網(wǎng)絡(luò)帶寬負(fù)擔(dān)。Masri等[19]研究一種延遲反饋速度控制器,采用非線性單自由度模型對諧振器響應(yīng)進(jìn)行模擬,繪制時(shí)滯反饋控制下諧振器振動(dòng)系統(tǒng)安全域,與比較安全域侵蝕程度來直觀地描述電容型微諧振器吸合不穩(wěn)定現(xiàn)象。這些研究原具有描述微結(jié)構(gòu)吸合不穩(wěn)定現(xiàn)象,但對其發(fā)生控制機(jī)制相關(guān)研究報(bào)道極少,仍有待進(jìn)一步開展。
因此,本文以一類典型的梳齒型微機(jī)械陀螺結(jié)構(gòu)為研究對象,針對其非線性因素導(dǎo)致的振動(dòng)跳躍、吸合不穩(wěn)定等機(jī)理提出時(shí)滯位置反饋控制。結(jié)構(gòu)如下:首先,對微陀螺系統(tǒng)進(jìn)行無擾動(dòng)分析;進(jìn)而,利用多尺度研究系統(tǒng)振動(dòng)跳躍現(xiàn)象及機(jī)制;最后,對微陀螺系統(tǒng)施加時(shí)滯位置反饋控制,研究吸合不穩(wěn)定現(xiàn)象及其控制,并給出結(jié)論與分析。
1 動(dòng)力學(xué)建模
(1)
(2)
式中:n為梳齒數(shù);l為驅(qū)動(dòng)梳齒重疊長度;a為驅(qū)動(dòng)梳齒厚度;sd為驅(qū)動(dòng)梳齒間隙;η為介電常數(shù)。驅(qū)動(dòng)方向右側(cè)和左側(cè)電壓分別為
Ud1=Ud0+Udacos(ωt),Ud2=Ud0-Udacos(ωt)
(3)
式中:Ud0為驅(qū)動(dòng)直流電壓;Uda為驅(qū)動(dòng)交流電壓幅值。驅(qū)動(dòng)方向的靜電力為[20]
(4)
式中:ω為激勵(lì)頻率;Ex與驅(qū)動(dòng)交流電壓幅值和驅(qū)動(dòng)直流電壓成正比,即為驅(qū)動(dòng)電壓相關(guān)參數(shù)。同理,檢測方向兩個(gè)電容表達(dá)式為
(5)
式中:ll和lw分別為檢測電極的長度和寬度;ss為檢測電極間隙;Us為檢測電壓。則檢測方向的靜電力可表示為
(6)
則式(6)中參數(shù)Ey隨檢測電壓Us單調(diào)遞增。在圖2中,設(shè)ad和as分別為驅(qū)動(dòng)方向和檢測方向加速度,則其滿足
(7)
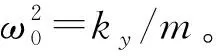
(8)
式中:驅(qū)動(dòng)電壓相關(guān)系數(shù)EX為驅(qū)動(dòng)交流電壓幅值Uda的正比例函數(shù);檢測電壓相關(guān)系數(shù)EY為檢測電壓的單調(diào)函數(shù)。則無量綱系統(tǒng)為
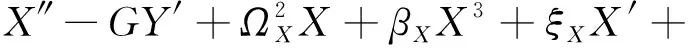
(9)
2 振動(dòng)跳躍現(xiàn)象及機(jī)理
本章主要討論系統(tǒng)的周期振動(dòng),若系統(tǒng)在固定參數(shù)下存在多穩(wěn)態(tài)解,則即便單個(gè)周期解穩(wěn)定,改變初始條件,系統(tǒng)仍會收斂到不同的周期吸引子,特別是初始條件的微小改變即引起系統(tǒng)動(dòng)力學(xué)行為的定性改變,即振動(dòng)跳躍。
首先,運(yùn)用多尺度方法對式(9)進(jìn)行分析,求解系統(tǒng)周期響應(yīng)以及穩(wěn)定性判斷,得出系統(tǒng)最終的幅頻響應(yīng)分岔方程,通過調(diào)節(jié)系統(tǒng)參數(shù)研究幅頻曲線圖的特征。引入小參數(shù)變量ε對系統(tǒng)進(jìn)行重新標(biāo)度,在主共振和1∶1內(nèi)共振情況,σ1和σ為驅(qū)動(dòng)方向的調(diào)諧參數(shù),0<ε?1。具體如下
(10)
將式(9)中常數(shù)項(xiàng)進(jìn)行平移代換,(Xc,Yc)為非零平衡點(diǎn),則可設(shè)
(11)
即滿足
(12)
式中,F(xiàn)Y為高階非線性項(xiàng),且|y|?1,將FY泰勒展開,保留Y的三次方,可得
FY=Y+2Y3
(13)
另外,將系統(tǒng)中檢測電壓相關(guān)參數(shù)EY進(jìn)行重新標(biāo)度,設(shè)
(14)
將式(10)~式(14)代入式(9)中,得到
(15)
在此基礎(chǔ)上,設(shè)方程的解形式為
(16)
式中:T0=T;Ti=εTi,(i=0,1,2,…)。采用多尺度法對系統(tǒng)進(jìn)行攝動(dòng),為使驅(qū)動(dòng)和檢測模態(tài)位移解不出現(xiàn)久期項(xiàng),通過對比ε0和ε1系數(shù),得到
X0=A1(T1,T2)eiT0+CC,Y0=B1(T1,T2)eiT0+CC
(17)
其中,
(18)
得到平均方程
(19)
將式(19)代入原系統(tǒng)參數(shù)還原可得到微陀螺系統(tǒng)關(guān)于振幅a1,b1的分岔方程
(20)
由式(18)和式(20)確定式(15)的近似周期解。根據(jù)式(19),系統(tǒng)周期解所對應(yīng)特征方程為
(21)
由于系統(tǒng)Hopf分岔的臨界條件為式(21)有純虛根,即
g1-g2(ξX+ξY)=0
(22)
其中,
(23)
以下通過分岔方程式(20)來繪制微機(jī)械陀螺幅頻特性響應(yīng)。其中,系統(tǒng)參數(shù)取值如下
G=0.01,Ad=0.4,As=0,ξX=ξY=0.015,
(24)
激勵(lì)幅值對驅(qū)動(dòng)方向系統(tǒng)振幅的影響,如圖3所示。由圖3可知,系統(tǒng)在共振點(diǎn)附近響應(yīng)幅值較大,相對應(yīng)的輸出信號會比較明顯,有利于檢測;然而,當(dāng)電壓頻率大于固有頻率且偏高時(shí),系統(tǒng)出現(xiàn)多個(gè)解支,對應(yīng)圖中兩條縱向虛線之間的三條解支:明顯地,有雙穩(wěn)態(tài)周期振動(dòng)共存;特別地,激勵(lì)頻率從1.025增大到1.03系統(tǒng)的動(dòng)力學(xué)行為對初始條件更敏感,如圖4和圖5所示。在圖4中,當(dāng)Ω=1.025時(shí),存在雙穩(wěn)態(tài)現(xiàn)象,如實(shí)虛兩種線型對應(yīng)的振動(dòng)解所示,其吸引域的投影如圖5(a)和圖5(b)所示。由于[X(0),X′(0),Y(0),Y′(0)]=(0,0,0,0)這個(gè)初始狀態(tài)更受關(guān)注,為直觀描述:當(dāng)繪制檢測方向吸引域時(shí),假定驅(qū)動(dòng)方向X(0)=X′(0)=0;當(dāng)繪制驅(qū)動(dòng)方向吸引域時(shí),假定檢測方向Y(0)=Y′(0)=0。因此,得到圖5在其領(lǐng)域內(nèi)吸引域的投影。在圖5中,不同穩(wěn)態(tài)運(yùn)動(dòng)對應(yīng)的吸引域以黑色或灰色標(biāo)出,系統(tǒng)存在兩種穩(wěn)態(tài)運(yùn)動(dòng),其中振動(dòng)幅值小的穩(wěn)態(tài)吸引域?qū)?yīng)淺灰色,振幅大的穩(wěn)態(tài)吸引域?qū)?yīng)深灰色,并以“+”標(biāo)出相對零平衡點(diǎn)位置。由圖5(a)、圖5(b)可知,零狀態(tài)時(shí)對應(yīng)大振幅周期振動(dòng),但當(dāng)Ω增大到1.03,如圖5(c)和圖5(d)所示,對應(yīng)的是小振幅落到了淺灰區(qū)域,同時(shí),由圖5可知,零初始條件附近,初始條件的微小擾動(dòng)極易造成振動(dòng)跳躍。不僅如此,當(dāng)Ω=1.03時(shí),檢測方向的吸引域出現(xiàn)分形邊界,而在邊界之外對應(yīng)的白色區(qū)域則表示吸合區(qū)域,即檢測方向極板吸合,說明系統(tǒng)容易發(fā)生吸合不穩(wěn)定現(xiàn)象,其行為和機(jī)制將在第3章討論。
3 吸合不穩(wěn)定現(xiàn)象分析
由于吸合不穩(wěn)定現(xiàn)象屬于全局分岔行為,而對于同異宿分岔大多是運(yùn)用Melnikov方法[21]分析其必要條件。因此,以下將討論全局分岔機(jī)理。
3.1 無擾動(dòng)分析
系統(tǒng)參數(shù)取值見式(24),代入式(12)得Yc=0,將式(10)~式(12)代入式(9)中,得
(25)
將式(25)整理成含有擾動(dòng)項(xiàng)的規(guī)范型,得
(26)
(27)
滿足哈密頓系統(tǒng),其哈密頓量函數(shù)為
(28)
在圖6(a)中,只有繞O點(diǎn)的極限環(huán),令
(29)
式中,Qc為常數(shù),則
(30)
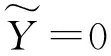
(31)
因此,有
(32)
從而解得對應(yīng)邊界上Qc,如圖6(a)中加粗曲線所示。在該異宿軌道內(nèi)部,圍繞原點(diǎn)中心,軌線閉合有界;封閉異宿軌道外,軌線溢出,即容易發(fā)生過度振動(dòng),對應(yīng)微結(jié)構(gòu)靜態(tài)吸合。
考慮到異宿軌道,有
(33)
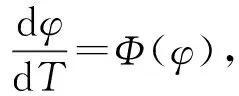
φ(-∞)=0,φ(0)=φ0,φ(+∞)=π
(34)
小擾動(dòng)下異宿軌道精確解析解可設(shè)為三角函數(shù)表示,根據(jù)圖6,對異宿軌道可以設(shè)為
(35)
并結(jié)合式(32)得到
(36)
(37)
根據(jù)式(34)和式(36),異宿軌道可解析表達(dá)為
(38)
且根據(jù)式(33)得
(39)
3.2 異宿分岔?xiàng)l件
將異宿軌道及時(shí)間T關(guān)于φ的表達(dá)式代入Melnikov函數(shù),并還原為式(9),得到Melnikov函數(shù)為
(40)
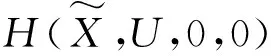
(41)
明顯有I1>0。引起原系統(tǒng)異宿分岔的必要條件是Melnikov函數(shù)存在簡單零點(diǎn),因此,令M2=0,則可將耦合項(xiàng)表達(dá)為
(42)
代入M1,當(dāng)M1當(dāng)存在簡單零點(diǎn),有
(43)
還原系統(tǒng)參數(shù)引起異宿分岔的參數(shù)EX滿足
(44)
4 時(shí)滯反饋控制機(jī)理
為抑制系統(tǒng)振動(dòng)跳躍和吸合不穩(wěn)定現(xiàn)象,通過在式(1)的驅(qū)動(dòng)電壓上施加線性時(shí)滯位置反饋控制,時(shí)滯位置反饋控制系統(tǒng)表達(dá)為
(45)
(46)
則時(shí)滯控制系統(tǒng)成為
(47)
實(shí)施該控制的前提是線性化系統(tǒng)仍不會因時(shí)滯項(xiàng)的出現(xiàn)發(fā)生平衡點(diǎn)穩(wěn)定性切換。這里由于時(shí)滯項(xiàng)加在激勵(lì)項(xiàng)當(dāng)中,因此,并不會引起線性系統(tǒng)平衡點(diǎn)的穩(wěn)定性發(fā)生切換。
數(shù)值模擬式(47)驅(qū)動(dòng)方向幅頻響應(yīng)特性曲線,如圖8所示,其中,給定增益系數(shù)Gp=0.2。在圖8中,明顯可見,隨著時(shí)滯量的增加,從0.3~0.8,盡管系統(tǒng)振幅有所減小,但幅頻響應(yīng)特性曲線由原來的多穩(wěn)態(tài)解共存變成單支連續(xù)周期解,即全局穩(wěn)定,因此,振動(dòng)跳躍現(xiàn)象可以得到有效抑制。
下面將開展對時(shí)滯反饋控制系統(tǒng)異宿分岔行為機(jī)制的研究,從而分析時(shí)滯位置反饋對這類復(fù)雜動(dòng)力學(xué)行為的控制機(jī)理及效果。由于時(shí)滯反饋項(xiàng)并不帶來系統(tǒng)穩(wěn)定性定性改變,因此,將式(47)中時(shí)滯項(xiàng)進(jìn)行二階泰勒展開,其相應(yīng)Melnikov函數(shù)為
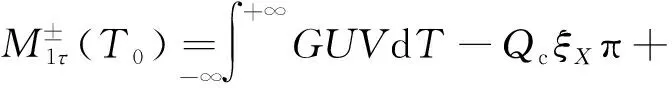
(48)
其中,
(49)
由于本文討論主共振情況,即Ω位于1的領(lǐng)域,因此,I2>0。根據(jù)式(49),Melnikov函數(shù)存在簡單零點(diǎn)的時(shí)滯位置反饋控制下系統(tǒng)驅(qū)動(dòng)電壓幅值滿足
(50)
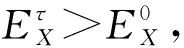
進(jìn)而對該控制效果進(jìn)行數(shù)值模擬,對無量綱控制系統(tǒng)式(47),由于零時(shí)刻前無反饋信號輸入,即當(dāng)-τ≤T<0時(shí)有初始狀態(tài)[Y(T),Y′(T)]=(0,0),則其初始狀態(tài)空間同樣可投影到零時(shí)刻初始狀態(tài)平面[Y(T),Y′(T)]上。不同電壓下系統(tǒng)的安全域隨時(shí)滯量和驅(qū)動(dòng)電壓幅值的變化,如圖10所示。圖10(a)~圖10(c)為當(dāng)τ=0時(shí)無控制微陀螺振動(dòng)系統(tǒng)的安全域演變情況,對比可知,隨著EX增大,安全域分形逐漸明顯,當(dāng)EX=0.02時(shí),見圖10(a),無控制系統(tǒng)安全域開始出現(xiàn)不光滑邊界。當(dāng)τ從0開始增大,分別對比圖10(a)、圖10(d)、圖10(g)和圖10(b)、圖10(e)、圖10(h),可見系統(tǒng)安全域邊界變光滑,而且面積逐漸增大,安全域侵蝕得到有效抑制。而當(dāng)EX=0.6,在不施加控制時(shí),系統(tǒng)安全域被嚴(yán)重侵蝕,對比圖10(c)、圖10(f)、圖10(i),當(dāng)增大時(shí)滯量,即便邊界未變光滑,但安全域侵蝕狀態(tài)也得到明顯改善;原點(diǎn)鄰域逐漸變得安全,表明時(shí)滯量的增大能抑制吸合不穩(wěn)定現(xiàn)象。由此可見,時(shí)滯位置反饋對抑制這類微陀螺結(jié)構(gòu)吸合不穩(wěn)定具有良好的控制效果。
5 結(jié) 論
以一類典型的靜電驅(qū)動(dòng)微機(jī)械陀螺動(dòng)力學(xué)模型為研究對象,首先,建立微陀螺結(jié)構(gòu)的二自由度動(dòng)力學(xué)模型,運(yùn)用多尺度法和分岔理論,結(jié)合數(shù)值驗(yàn)證,分析系統(tǒng)參數(shù)引起的微陀螺多穩(wěn)態(tài)響應(yīng);其次,通過引入獨(dú)立參數(shù),得到異宿軌道的精確表達(dá)式,在此基礎(chǔ)上利用Melnikov方法預(yù)測微結(jié)構(gòu)的異宿分岔?xiàng)l件,從而分析引起微結(jié)構(gòu)檢測方向吸合不穩(wěn)定的機(jī)制,并提出在系統(tǒng)驅(qū)動(dòng)電壓上引入線性時(shí)滯位置反饋,從而抑制該現(xiàn)象,數(shù)值算例與理論算例解析結(jié)果的吻合證明了理論預(yù)測的有效性。主要得到以下結(jié)論:
(1) 在主共振和1∶1內(nèi)共振的情況下,微陀螺系統(tǒng)容易出現(xiàn)多穩(wěn)態(tài)和振幅跳躍現(xiàn)象。
(2) 驅(qū)動(dòng)交流電壓幅值增大容易引起檢測方向極板吸合不穩(wěn)定現(xiàn)象,該現(xiàn)象可歸因于異宿分岔。
(3) 當(dāng)反饋增益系數(shù)大于零時(shí),時(shí)滯位置反饋能夠有效地抑制微結(jié)構(gòu)的振動(dòng)跳躍和吸合不穩(wěn)定現(xiàn)象;時(shí)滯量和反饋增益系數(shù)作為獨(dú)立的兩個(gè)控制參數(shù),具有較大的參數(shù)取值范圍,說明時(shí)滯位置反饋?zhàn)鳛閱瓮ǖ揽刂品椒ǎ强刂七@類靜電驅(qū)動(dòng)微陀螺復(fù)雜動(dòng)力學(xué)行為的良好策略。
本文主要從理論上對微陀螺的振動(dòng)特性進(jìn)行了分析,為微機(jī)械陀螺的設(shè)計(jì)與優(yōu)化控制提供參考依據(jù)。為強(qiáng)化理論研究的實(shí)用性,使現(xiàn)有理論研究更具針對性,在未來的工作中,筆者將從試驗(yàn)角度對相關(guān)的結(jié)論開展進(jìn)一步的關(guān)聯(lián)性分析。

