振動波在質量偏心Timoshenko梁非連續處的傳播特性研究

王 劍， 袁秀峰， 胡永彪

(1. 法蘭泰克重工股份有限公司，江蘇 蘇州 215211； 2. 長安大學 工程機械系，西安 710064)

在分析船舶、艦艇低頻振動問題時，通常將船體、艇體簡化為梁模型[1-2]。由于空間限制或下潛需求，船舶或潛艇內部設備的布置存在非均勻性，導致質心往往在截面形心的下方。這種質量偏心梁模型在縱垂面的彎曲振動，會同時引起梁的縱向振動[3]。由于梁的縱向振動對應圓柱殼周向波數n=0的模態，其在殼體低頻聲輻射中占據主導地位[4]。實際的簡化梁模型中往往存在非連續性，比如支撐、邊界、變截面及轉角等，同時，考慮到振動的物理本質是波的傳播。因此，很有必要開展質量偏心梁的彎-縱耦合振動研究，尤其應從振動波的角度，通過觀測波在非連續處的反射與透射特性，來討論其彎-縱耦合效應。

針對載荷的復雜性[5]，或者梁截面的非對稱性所引起的耦合振動問題，趙曄等[6]針對船體的薄壁開口梁，虞愛民等[7]針對橢圓截面的實心梁，分別研究了彎曲與扭轉的耦合振動。但是，目前關于質量偏心梁在縱垂面彎曲振動引起縱向振動的討論較少。

由于可以更好地從物理角度解釋機理，大量學者研究了梁結構中振動波的傳播。Fahy[8]發現桿中的縱向波為非頻散的傳播波，Timoshenko梁中的彎曲波一組為衰減波；另一組為傳播波，且在梁的截止頻率處發生衰減波向傳播波的轉變。Ji等[9]利用截面變化改變彎曲波的波速，從而提高振動能量收集效率。Mead[10]從波傳播的角度，研究了周期支撐梁結構在對流壓力場下的動力學響應。Cheng等[11]分析了周期梁結構聲子晶體中彎曲波的頻散特性，尤其針對波數為復數的彎曲波進行了詳細討論。Mace等[12]利用有限元法分析了梁模型中的波數、群速度等，作者認為此方法最大的優勢是可以直接使用傳統有限元中梁的質量和剛度矩陣。針對周期支撐的梁結構[13]及包含集中質量塊的周期梁結構[14]，學者們研究了存在裂紋時，結構中振動波的特性。Kalkowski等[15]用試驗測量了變截面梁中的彎曲與縱向波數。Mace[16]及Mei等[17]分別針對Euler和Timoshenko梁，詳細分析了振動波在彈性支撐、邊界、變截面處的傳播特性，為利用行波法研究非連續復雜梁結構的動力學特性打下基礎。

可見，針對質量偏心梁中彎-縱耦合振動波在非連續處的傳播問題，相關研究還比較欠缺。

因此，本文在已經推導了質量偏心Timoshenko梁彎-縱耦合振動控制方程[18]，及上述研究的基礎上，將通過分析彎曲傳播波、彎曲衰減波、縱向波在梁結構非連續處的透射、反射特性，對振動波的耦合及轉變現象進行討論，進而從波的角度提供對復雜偏心梁彎-縱耦合振動的理解，并為其固有特性及響應的求解創造條件。

1 公式推導

在將艦船或潛艇等效為梁模型時，由于設備往往布置在船/艇身水平剖面以下，且其對整體的動力學響應主要影響體現為附加質量。因此，如圖1所示的質量偏心梁截面，偏心梁考慮了附加質量引起的形心與質心不重合。其中：D為形心；G為質量中心；e為梁質心和形心之間的距離。

由于梁的質心和形心不重合，梁的轉動將引起質心的縱向位移。而轉動造成質心的橫向位移屬于二階小量，可以忽略。梁微元轉動引起質心的縱向位移為eθ。同時質心的縱向運動誘使梁微元產生ρAe2dx的附加轉動慣量。

這里直接給出考慮質量偏心的Timoshenko梁彎-縱耦合振動方程如下，具體推導過程見附錄A

(1)

式中：ρ為梁的密度；A為截面面積；I為截面慣性矩；u為縱向位移；v為橫向位移；θ為截面轉角；E為彈性模量；k為截面的剪切系數；G為剪切模量。

采用分離變量法

(2)

代入式(1)得

(3)

若使式(3)有非零解，則其系數矩陣的行列式為零，由此可得到特征方程

E2kGI·S3+Eρω2(EI+2kGI+2kGAe2)·S2+
ρω2(2EIρω2+2EAe2ρω2+kGρIω2+kGρAe2ω2-
kGEA)·S+ρ2ω4[(I+Ae2)ρω2-kGA]=0

(4)

式中：S=λ2；ω為角頻率。

由于本模型不考慮阻尼，計算出的波數λ為實數或者純虛數，即式(4)有三個不等實根[19]，其開平方根后取正值

(5)

即式(4)共可求得六個波數，分為三組，每組內的兩個波數互為相反數，波數為正值時是負行波，為負值時是正行波。其中λ1，-λ1對應彎曲波中的衰減波； iλ2，-iλ2對應彎曲波中的傳播波； iλ3，-iλ3對應縱向波，是一種傳播波。

故而振型函數可表示為

(6)

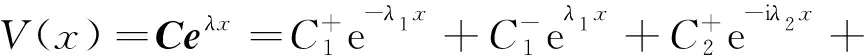
(7)

(8)

可以看出，上述三種位移均由彎曲衰減波、彎曲傳播波和縱向傳播波組成，振型系數Bj，Cj，Dj(j=1,2,3)右上角標取“+”時，為沿x軸正方向傳播的正行波；取“-”時，為沿x軸負方向傳播的負行波。

將振型函數表達式(6)～式(8)代入式(2)，進一步再代入控制方程式(1)，可以得到各組位移系數之間的關系

下面將考察振動波在彈性支撐、邊界、變截面處及轉角處的傳播情況。同時，為了消除同一模型中偏心率變化對振動波傳播特性分析的干擾，下面四個模型中均將偏心率設置為統一數值，即不考慮非連續處左右偏心率的變化。

1.1 彈性支撐處

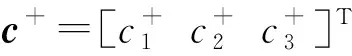
(9)

記x=0左側的位移分別為V-，U-，Θ-，右側分別為V+，U+，Θ+，即

(10)

(11)

(12)

(13)

(14)

(15)

在x=0處給出位移連續條件

V+=V-,U+=U-,Θ+=Θ-

(16)

力學平衡條件

KVV±+Q-=Q+,M--KRΘ±=M+,N++KNU±=N-

(17)

式中：N為軸向力；M為彎矩；Q為剪力。即[20]

(18)

將位移表達式(10)～式(15)代入位移連續條件式(16)，得到

(19)

其中，

將位移表達式(10)～式(15)，內力表達式(18)代入力平衡條件式(17)得

(20)

其中，

結合式(19)、式(20)，得到透射矩陣與反射矩陣

(21)

(22)

1.2 邊界處

如圖3所示，正行入射波c+在彈性邊界處反射，生成負行反射波c-。入射波與反射波之間的關系是

(23)

在x=0處的力平衡條件

Q-+KVV-=0，M--KRΘ-=0，N-+KNU-=0

(24)

將位移表達式(10)～式(12)，內力表達式(18)代入力平衡條件式(24)得

(25)

其中，

因此，彈性邊界處的反射矩陣為

(26)

1.3 變截面處

圖4所示的截面突變發生在x=0處，正行入射波c+在此處產生正行透射波g+及負行反射波c-。

變截面處透射矩陣、反射矩陣與振動波之間的關系見式(9)，變截面處兩端位移關系式見式(16)，力平衡條件為

Q-=Q+，M-=M+，N-=N+

(27)

將式(10)～式(15)代入位移連續條件式(16)得

(28)

其中，

將位移表達式(10)～式(15)，內力表達式(18)代入力平衡條件式(27)得

(29)

其中，

式中：幾何及材料參數下標1為左邊梁，下標2為右邊梁；波數和位移系數比例上標L為左梁，上標R為右梁。

結合式(28)、式(29)，得到透射矩陣與反射矩陣

(30)

(31)

1.4 轉角處

如圖5所示，在橫梁和豎梁90°轉角處，正行入射波c+在此處產生透射波g+及負行反射波c-，選擇轉角處為x=0。

根據圖5中位移及力的分析，在變截面處位移連續條件

力平衡條件

式中：下標1為橫梁的相關參數；下標2為豎梁的相關參數；下標J為連接塊的相關參數，字母J為連接塊的轉動慣量；“··”為對時間求兩階偏導；h1為橫梁截面寬度；h2為豎梁截面寬度。

消去連接塊的量，得到位移連續條件式(32)，力平衡條件式(33)

(32)

(33)

橫梁上的位移由正行波c+和負行波c-組成，因此其表達式為

(34)

(35)

(36)

豎梁上的位移由正行波g+組成，因此其表達式為

(37)

(38)

(39)

式中： 上標H為橫梁的相關參數；上標V為豎梁的相關參數。

將位移表達式(34)～式(39)及內力表達式(18)分別代入式(32)、式(33)，得到內力平衡方程組

(40)

其中，

位移連續方程組

(41)

其中，

結合式(40)、式(41)，得到透射矩陣與反射矩陣

(42)

(43)

2 算 例

表1給出了一個圓形截面梁的幾何與物理參數，其中：υ為泊松比；R為梁截面半徑；剪切因子k是根據Cowper[21]對圓形截面的研究所取。

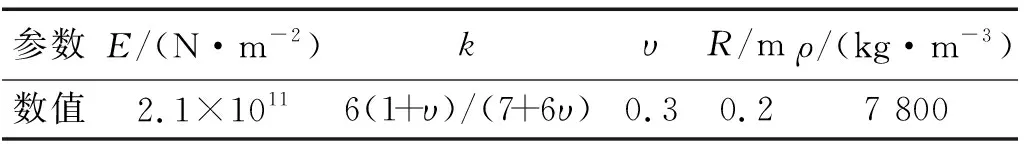
表1 計算模型的參數Tab.1 Parameters of the model

下面的算例基本采用表1中的參數，出現其他參數時會在相應算例中加以說明。

2.1 驗 證

從圖6可以看出，透射矩陣每列元素的幅值相等，反射矩陣每行的元素幅值相等，且本文推導結果與Mei等的研究結果完全吻合，證明了本文推導的正確性。

2.2 彈性支撐處

針對表1所給的模型參數，在其中部模擬簡支支撐。各質量偏心率下透射矩陣元素的幅值如圖7所示，反射矩陣元素的幅值如圖8所示。

由圖7可知，不存在質量偏心時：①彎曲波透射矩陣的每列元素幅值相等，即入射衰減波對透射衰減波和傳播波的貢獻度相等，入射傳播波也具有相同特點；②縱向波完全透射。

存在質量偏心時：①隨著質量偏心率的提高，截止頻率會下降，在ee=0.9時，截止頻率下降到未偏心的1/2左右，在圖7的黑色實線，也就是與透射衰減波有關的曲線中均有所體現；②入射衰減波對透射衰減波貢獻受偏心影響不大，一直處于主導地位，對透射傳播波貢獻度隨偏心率增大而減小，對透射縱向波的貢獻度隨著偏心率增大而增大；③入射傳播波對透射衰減波貢獻受偏心影響不大，超過截止頻率后一直處于次要地位，對透射傳播波及縱向波的貢獻度，隨著偏心率增大而增大；④入射縱向波對透射傳播波及縱向波在低頻時貢獻較大，隨著頻率及偏心率的增大，其對透射的三種波型貢獻明顯減小。

對于反射特性，不存在質量偏心時：①彎曲波反射矩陣的每行元素幅值相等，即入射衰減波及傳播波對反射彎曲波擁有同樣的貢獻度，其中，對反射衰減波的貢獻度均較小，對反射傳播波的貢獻度均較大；②縱向波無反射。

存在質量偏心時：①反射矩陣中每一列的元素幅值相等，也就是說入射的三種波型對反射波有相同的貢獻；②以入射衰減波為例，它對反射衰減波貢獻度受偏心影響不大，但其對反射傳播波及縱向波的貢獻度，隨著頻率及偏心率的增大，分別減小和增大。

2.3 邊界處

針對表1所給的模型參數，在其右端模擬簡支支撐，由于不存在透射，只給出反射曲線，如圖9所示。

從圖9可以看出，反射矩陣對角元素的幅值是1，非對角元素均為零，也就是說三種入射波型并不會產生耦合和轉變，并且質量偏心對此并無影響。

2.4 變截面處

三組入射波從半徑為0.2 m的梁段入射至0.15 m的梁段，其他參數與表1一致，其透射矩陣第1、第2、第3列元素的幅值如圖10所示；其反射矩陣第1、第2、第3列元素的幅值如圖11所示。

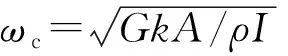
通過圖11可以看出，反射矩陣并不是對角占優矩陣，彎曲衰減波對反射彎曲傳播波的貢獻隨著偏心率的增大而減小，彎曲傳播波對反射彎曲傳播波及縱向波的貢獻，隨著偏心率的增大而增大，在偏心率ee>0.6 時尤為顯著。

2.5 轉角處

三組入射波從半徑為0.2 m的橫梁入射至0.15 m的豎梁，其他參數與表1一致，其透射矩陣第1、第2、第3列元素的幅值如圖12所示。其反射矩陣第1、第2、第3列元素的幅值如圖13所示。

從圖12可以看出，透射矩陣第1列元素的幅值在豎梁截止頻率處均有波谷，即三組入射波在豎梁截止頻率處對彎曲衰減波的貢獻均為極小值，在變截面處，即圖10中亦有此特點。隨著偏心率的增大，彎曲衰減波、傳播波對縱向波的貢獻均變大，而縱向波對彎曲波的貢獻卻變小。

從圖13可以看出，圖13(b)、圖13(c)中黑色曲線在橫梁截止頻率處均有波谷，即彎曲傳播波與縱向波在橫梁截止頻率處對彎曲衰減波的貢獻均為極小值，此特點與變截面處，即圖11中所示亦相同。隨著偏心率的增大，彎曲衰減波、傳播波對縱向波的貢獻均變大，而縱向波對彎曲波的貢獻卻變小。

3 結 論

本文針對質量偏心梁的彎-縱耦合振動，以彎曲衰減波、彎曲傳播波、縱向波這三組波的反射與透射為研究對象，推導了在彈性支撐處、邊界處、變截面處、轉角處的反射、透射矩陣，并給出算例，重點分析了質量偏心下這三組波的耦合與波型轉變。得到以下結論：

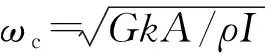
(2) 隨著偏心率或頻率提高，彎曲波對縱向波貢獻變大。通過式(3)得到的系數B和C關系式可以看出，縱向波系數與彎曲波系數之間的比值與eω2成正比。因此，彎曲波在偏心率或頻率提高時，其對縱向波貢獻變大。

(3) 在邊界處，三種入射波型并不會產生耦合和轉變，并且質量偏心對此無影響。

(4) 波入射位置存在截面尺寸變化時，彎曲衰減波的透射系數在新尺寸對應的截止頻率處有極小值。這是由于彎曲衰減波在此截止頻率處轉變為了彎曲傳播波。

附錄A

對于正文圖1中的梁單元，根據縱向力平衡關系

(A.1)

根據剪力平衡關系

(A.2)

根據彎矩平衡關系

(A.3)

式中：Q為剪切力；N為軸向力；M為彎矩；γ為剪切應變；θ為轉動角度；v為梁的橫向位移；u為梁的縱向位移；I為梁截面的截面慣性矩；ρ為梁的密度；A為梁的截面面積，本文研究對象是沿長度方向均勻的梁，因此上述梁的幾何參數和物理參數沿梁的長度方向均為常數。

Timoshenko梁中內力和位移之間的關系為

(A.4)

(A.5)

(A.6)

將式(A.4)～式(A.6)代入式(A.1)和式(A.2)，經過整理，即可得到質量偏心Timoshenko梁的彎-縱耦合控制方程式(A.7)，即正文中的式(1)。

(A.7)