基于改進滑模趨近律的振動基機械臂的有限時間軌跡跟蹤控制
郭宇飛, 許盛悅, 李慧子, 王志剛, 郝志強
(1. 武漢科技大學 冶金裝備及其控制教育部重點實驗室,武漢 430081;2. 武漢科技大學 精密制造研究院,武漢 430081;3. 武漢科技大學 機器人與智能系統研究院,武漢 430081; 4. 中國艦船研究設計中心,武漢 430064)
隨著機器人技術的不斷地發展,機械臂的應用越來越多樣化,人們對其性能寄寓了更高的期望。振動基機械臂[1]是一類安裝基座存在隨機振動的機械系統的總稱,包括:太空自由漂浮機械臂[2]、水下作業機械臂[3]、水面起重機[4]、坦克彈藥傳輸機械臂[5]等。受基座振動帶來的非線性耦合力的影響,振動基機械臂的控制一直都是相關領域的研究的熱點和難點。“如何抑制基座振動的影響,實現機械臂系統的精確位置和軌跡跟蹤控制”,吸引了許多學者的關注。
根據機械臂的任務空間的不同,振動基機械臂通常可以分為以下兩類:一類是全局坐標振動基機械臂,機械臂工作在全局笛卡爾坐標系下,例如太空自由漂浮空間機械臂、水下作業機械臂、水面起重機等;另一類是隨動坐標振動基機械臂,機械臂工作在基座的隨動坐標系下,如坦克彈藥傳輸機械臂等。
對于第一類振動基機械臂,現有控制策略大多基于基座振動可測或可預估的前提,然后進行系統的解耦和補償控制。如Toda等[6]將海浪擾動假設在已知頻率范圍內,簡化了振動基系統并提出了一種基于線性H∞的控制方法,實現了振動基系統的魯棒軌跡跟蹤控制。Küchler等[7]將海上起重機非線性模型的輸入、輸出線性化,并結合卡爾曼濾波方法對波浪運動進行預測,實現了起重機的升降魯棒控制。Chu等[8]為解決船體垂直垂蕩運動對海上起重機運輸的影響,提出用神經網絡的船舶運動預測方法對系統進行主動補償。對于第二類振動基機械臂系統,基座振動產生的非線性耦合力(如離心力、科氏力等)更加復雜,其控制器的設計也更具挑戰。坦克彈藥傳輸機械臂是這類系統的典型代表。如圖1所示,坦克車體(基座)在受到來自火炮后坐力和不平路面的共同激勵,對傳輸機械臂系統產生難以測量和預估的基座振動,因此對控制器的魯棒性要求較高。
對坦克彈藥傳輸機械臂的前期研究中,基于隱式Lyapunov方法的連續型反饋控制方法[9]和基于分段線性反饋控制算法[10],已被證明夠克服車體振動的干擾,具有良好的魯棒性。但是上述方法并未考慮控制器的有限時間性能。有限時間控制是一些振動基機械臂在實際中面臨的另一個難點,如何實現坦克彈藥傳輸機械臂的快準裝填面臨著巨大挑戰。
滑模控制,因為其對系統模型依賴性較小,在系統受到外界干擾和參數攝動時具有不變性,是一種魯棒性、抗干擾性強的非線性控制方法,已被廣泛應用在振動基機械臂的控制器設計中。Kim等[11]將四旋翼無人機和機械臂作為一個組合系統建立動力學模型,設計一種自適應滑模控制器并完成無人機機械臂的拾取控制;Ngo等[12]考慮到海浪等因素對水面起重機產生影響,設計一種新的滑模面并結合電車動力學、船舶動力學與搖擺動力學提出滑模控制方法很好的消除了系統的橫向搖擺干擾;Iwamura等[13]通過引入一個非線性滑模面來實現對振動基機械臂的變增益積分控制。
滑模控制本質上是一種變結構控制方法,系統狀態在達滑模切換面附近時系統慣性必然存在,這也使得在實際中滑模控制系統的抖振必然存在[14]。為了改善滑模控制抖振問題,高為炳院士[15]首先將趨近律運用在滑模控制中,并提出了等速趨近律、指數趨近律、冪次趨近律和一般趨近律。
通過趨近律的設計,除了可以抑制抖振還能調節到達滑模面的速率,進而實現快速控制。廖瑛等[16]提出一種雙冪次的組合趨近律,并利用fal函數的性質加快了趨近速率。王要強等[17]在傳統冪次趨近律的基礎上,加入指數項并且在冪次項指數中引入系統狀態變量,使系統能平穩進入滑模面并解決了冪次趨近律遠離滑模面趨近速度慢的缺點。鄭美茹等[18]利用分數階次積分型符號函數特性,有效解決滑模控制中趨近速度和抖振程度間的矛盾,但控制器設計復雜實現不易。Pan等[19]將冪次趨近律與等速趨近律相結合提出改進的趨近律,來實現變結構控制的全局快速收斂性,但是抖振問題仍然間斷性而存在。
本文以坦克彈藥傳輸機械臂為背景,針對一類基座振動未知的隨動坐標系振動基機械臂,設計了一種快速的軌跡跟蹤控制器。具體上,提出一種新型的對數冪次趨近律,然后結合快速終端滑模面提出一種新型的有限時間滑模控制算法,最后基于雙環控制策略在Labview環境下搭建了系統的控制回路。試驗結果證明了所設計控制器的有效性。
1 系統動力學分析
對于圖1所示的傳輸機械臂系統,將來自車體的強烈擾動視為系統的外部干擾,采用拉格朗日法將其動力學模型由二階非線性微分方程表示為
(1)
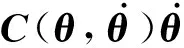
性質1慣量矩陣H(θ)為正定對稱矩陣,且上下有界,即對任意向量λ有
mλ2≤‖λTHλ‖≤Mλ2
式中, 0 性質2系統的慣量矩陣H(θ),其偏微分大小具有有界性,即‖?H(θ)/?θi‖≤N(N>0)。 性質3存在常數S0>0,使得系統的基座擾動力項S滿足‖S‖≤S0。 在滑模變結構控制中,將系統的滑模運動分為兩個過程:趨近運動和滑模運動。趨近運動是指系統在軌跡跟蹤的過程中從任意系統狀態到滑模面的運動。為了提高趨近運動的性能,許多學者將改進的指數[20]、冪次[21]函數以及其他非線性函數[22]應用在趨近律函數中,但是目前對數函數在趨近律的研究中卻極少。本文將對數函數引入趨近律中,提出了一種新的對數冪次趨近函數,趨近律方程為 (2) 式中: 0<α<1;ν為正偶數;K1,K2,K3>0。 由式(2)可知對數冪次趨近律函數由三項組成,式中第一項在滑模狀態遠離滑模面時起主導作用,后二項在滑模狀態趨近于滑模面時起主導作用。通過合理的選擇參數可以提高系統趨近運動的速度并抑制滑模抖振。 為了與不同趨近律函數的比較,將式(2)與下列三種常見的趨近律方程列舉出來,代數式中選擇相同的系數常數并畫出方程曲線。 (1) 指數趨近律 (3) (2) 快速冪次趨近律[23] (4) (3) 雙冪次趨近律[24] (5) 式中:K1=K2=K3=5;α=0.5,β=1.5,ν=4。 在圖2中,橫坐標表示滑模趨近運動的滑模狀態,縱坐標表示趨近運動中的趨近速率。從圖2中四種趨近律函數的比較可以看出,當滑模狀態在σ=0(滑動模態區)附近時,對數冪次趨近函數的值小于其他三種趨近函數,減小了滑模狀態在滑模面上切換時的速率,從而減小系統慣性,使滑模狀態較平滑的進入滑模面來減弱抖振現象;當滑模狀態遠離σ=0附近時,對數冪次趨近函數值大于其他三種趨近律函數,滑模狀態可以更快的趨向滑動模態區。綜上述,合理選擇對數冪次趨近律參數可以使系統提高收斂速度并在滑模態附近有效的緩解系統抖振。 接下來將為對數冪次趨近律的有限時間特性進行驗證。 引理1針對非線性系統,若存在定義在包含原點鄰域U?Rn內的連續可微的正定函數V(x),滿足 (6) 定理1式(2)將在有限時間內收斂至平衡點領域內,有限時間為Tq。 證明:選擇Lyapunov函數為 V(σ)=σ2/2 (7) 將式(2)代入求導后的式(7)得 (8) 由引理1可知c=K32^(3+α/4),κ=(3+α)/4, 式(2)將在有限時間內收斂于平衡點領域,有限時間Tq為 (9) 滑模變結構控制中,滑模運動目的是讓系統的軌跡狀態到達滑模面后能夠漸近趨于原點收斂。傳統的終端滑模面在接近原點時具有快速收斂能力,但是在遠離原點時,收斂速度低于線性滑模面。快速終端滑引入線性項,解決了這一問題。考慮振動基機械臂在外界干擾下系統狀態的不確定性強,選擇傳統滑模面將為機械臂的軌跡控制帶來了許多不可控的問題。所以,本文將采用一種快速終端滑模面,通過對滑模面的參數設計可確定滑模運動的收斂時間上界。滑模面設計如下 (10) 式中:θd為期望軌跡;μ,λ均大于0;l,m,p,r為正奇數且滿足l>m,r>p。給出式(10)的有限時間收斂上界ts[25]。 (11) 結合定理1可知,滑模變結構控制中滑模運動過程和趨近運動過程均可完成有限時間內收斂,由此可知,基于式(2)和式(10)的滑模控制方法可以實現系統的有限時間全局收斂穩定,收斂時間上限為ta=tq+ts具體表達式為 (12) 為得到本文方法的控制項,將式(1)代入求導后的式(10)可得 (13) 使用魯棒項Ur=ξtanh(σ)替代S,其中ξ>S0,將式(2)與式(13)結合,可得出振動基機械臂系統的控制項為 (14) 為了不失一般性,本文根據坦克彈藥傳輸機械臂的工作特性搭建垂直振動基-二連桿機械臂試驗臺來驗證控制方法的有效性。將試驗臺主體分為振動基座、連桿1、連桿2三個部分,在基座下加入垂直振動干擾如圖3所示。 試驗臺所選的關節電機型號為瑞士Maxon514100,控制器為EPOS2數字控制器,通過USB與上位機交換數據。振動基座底部的振動機構可產生振幅為77.05 mm 頻率為1.5 Hz的垂直正弦基座振動干擾。試驗平臺響應時間約3 s。試驗臺的動力學模型圖如圖4所示。 對應式(1)中動力學系統各個矩陣的具體表達式為 式中:連桿質量和長度分別為m2=m3=0.228 kg,L2=L3=0.21 m;電機關節質量md3=0.61 kg;關節的驅動轉動慣量分別為Jd2=0.000 018 1 kg·m2,Jd3=0.000 019 04 kg·m2; 關節1和關節2的相對質心的轉動慣量J2=J3=0.000 005 kg·m2。 為驗證本文控制方法對基座振動干擾和負載變化的魯棒性以及本文控制方法的優越性。設置三組試驗,如表1所示。 表1 試驗分組表Tab.1 Table of experiments 將試驗1設置為標稱試驗組,分別與變負載試驗組(試驗2)和對比試驗組(試驗3)進行對照來驗證所提出控制方法的有效性。設置試驗時長為100 s。期望軌跡為 (sin 0.5t,0.5cos 0.5t,sin 0.5t,0.5cos 0.5t) 試驗1:為了驗證本文所設計的控制器對的有效性,針對振動基試驗臺進行軌跡跟蹤控制,控制參數為K1=13,K2=15,K3=5,α=0.5,ν=2,μ=15,λ=5,l=p=3,ξ=5.5,m=1,r=5,試驗曲線如圖5~圖7所示。 由圖5~圖7可知,本文所設計的控制器,在垂直振動的干擾下表現出良好的跟蹤性能。由圖5(a)可知,電機關節1在啟動后用時0.883 s完成有效的位移軌跡跟蹤控制。跟蹤位移軌跡平穩,在軌跡波峰及波谷處有最大穩態誤差約為0.035 rad;由圖5(b)可知,電機關節2在平臺響應時間內自轉,控制啟動后實際軌跡迅速趨向期望軌跡,用時2.79 s完成有效的跟蹤控制,跟蹤位移軌跡平穩,穩態誤差約為0.02 rad;由圖6可知,在保證機械臂的位置控制前提下,機械臂的速度也能很好的跟蹤期望曲線。由圖7中電流響應曲線可知,并未出現傳統滑模控制中強烈的抖振現象。綜上述,本文所提出的控制器在基座振動的干擾下對機械臂的位移的軌跡跟蹤表現出了具有良好的控制性能,同時對速度也具有良好的跟隨性,在控制過程中未出現強烈的抖振現象。 試驗2:為了驗證本文所提出的控制方法對系統有效載荷具的不確定性具有魯棒性,將負載質量增加0.125 kg加載位置為位于末端連桿即連桿2的質心處,試驗臺和控制器的其他參數與試驗1保持一致。 試驗結果如圖8~圖10所示。試驗響應的試驗結果和預期情況一致,改變負載后,系統達到有效跟蹤時間相比試驗1有所變化,關節1有效跟蹤所用的時間減少了0.383 s,但是關節2有效跟蹤所用的時間增加0.495 s。除此之外,對于系統的穩態誤差和跟蹤表現基本沒有異樣,這表明了該控制方法對負載變化具有較好的魯棒性。 試驗3:為驗證本文所提出的控制方法的優越性,對振動基機械臂系統進行了一組對比軌跡跟蹤控制試驗。保持試驗臺的其他參數不變,將傳統的滑模軌跡跟蹤控制器代替本文的改進滑模控制器,控制器方程為 (15) 式中:μ=3;K1=1;ξ=7。 由圖11可見,在無基座振動干擾的條件下,關節1的位移軌跡跟蹤基本能實現,但曲線在跟蹤過程中具有小幅震蕩現象;在加入基座振動后,關節1無法完成軌跡跟蹤任務,位移跟蹤曲線在35.62 s,48.78 s,88.43 s 處均出現脫離期望軌跡的現象。這可能與關節1電機與振動基座固定安裝,受到的振動影響較直接有關;關節2的位移軌跡跟蹤曲線在有、無基座振動的條件下,試驗曲線相似,主要區別在于加入基座振動后位移曲線在趨近期望軌跡過程中有小幅波動。由圖12和圖13明顯可見,傳統滑模控制方法下,系統的速度響應和電流響應曲線震蕩幅值較大。表明了傳統滑模方法并不能克服基座振動干擾,并且具有明顯的抖振現象。 綜上所述,結合試驗1、試驗2可知,本文提出的控制器對于不確定的有效載荷具有較好的魯棒性,結合試驗1、試驗3可知,本文所提出的改進滑模控制器相比于傳統的滑模控制方法對于基座振動干擾具有更好的魯棒性,且具有較好的控制響應速度和控制精度,并且可以有效地抑制滑模的抖振現象。 (1) 以坦克彈藥傳輸機械臂為背景,研究在基座垂直振動以及有效載荷不確定的條件下機械臂的軌跡跟蹤問題,建立了包含基礎振動干擾項的拉格朗日動力學方程。 (2) 設計了一種新型對數冪次滑模趨近律并結合快速終端滑模面提出了改進型的滑模控制方法,并證明此滑模面和趨近律組合的控制器具有有限時間收斂的特性。 (3) 搭建簡化試驗臺驗證所提出的控制方法的魯棒性和優越性。與傳統的滑模控制方法相比,本文提出的方法對基座的垂直振動干擾的抑制能力較強,響應速度較快,控制精度較高。 (4) 本文控制器的設計方法不僅僅只適用受到強基座振動干擾的坦克彈藥傳輸機械臂,對與其他受到弱基座振動干擾的系統比如移動車載機械臂、無人機機械臂等同樣具有工程參考意義。2 控制器設計
2.1 趨近律的設計
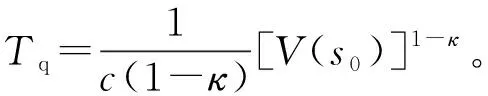
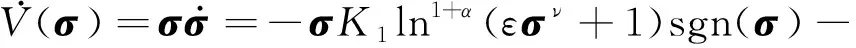
2.2 改進滑模控制器設計
3 試驗設計及驗證
3.1 試驗臺介紹
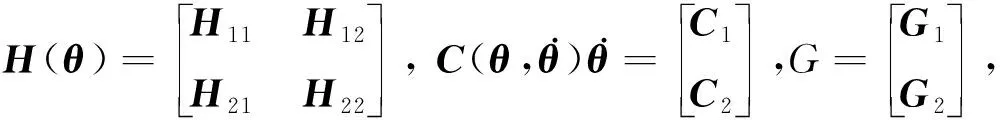
3.2 試驗驗證

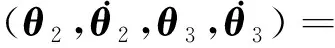
4 結 論

