門式框架結構平面外的動力失穩試驗研究

沈 超， 張 愿， 李遇春

(同濟大學 土木工程學院, 上海 200092)

門式框架是一種常見的工程結構型式，門式框架橫梁可能受到周期荷載的作用，如電機轉子的不平衡產生的周期荷載等。當周期荷載的頻率約等于結構(或子結構)自振頻率的兩倍時，結構系統可能發生動力失穩或參數共振[1]。與普通共振[2]不同，參數共振屬于非線性共振現象，外周期荷載作用方向與結構振動方向垂直，參數共振時，微小的激勵會引發大幅度的動力響應，其危害性巨大。門式框架結構一般在其平面內具有比較大的剛度，但其平面外剛度一般較小，更容易發生參數共振或動力失穩。

關于結構的參數共振研究，Xie、Bolotin[3]與Majorana等[4]研究了不同支撐條件下單跨梁的參數振動問題；Mishra等[5]研究了橫向裂紋梁的參數失穩問題；Fu[6]研究了耦合擺梁系統的參數共振問題，并給出其動力學軌跡；Carboni等[7]等研究了在面內激勵的非線性壓電梁的參數共振問題；Catellani等[8]采用Galerkin法分析了具有幾何缺陷的圓柱殼參數不穩定性問題；鐘子林等[9]對矩形薄板的參數共振失穩進行了理論與試驗分析。

當結構由多個構件組成時，結構系統會產生所謂的自參數共振。Tondl等[10]給出了自參數共振的定義，當結構由兩個子系統組成時：一個子系統稱為主系統；另一個子系統稱為次系統，主系統在外部周期荷載的作用下產生振動，那么主系統的振動將作為次系統的參數激勵，這種次系統在主系統振動激勵下的參數共振稱為自參數共振。在自參數共振系統中，當次系統的固有頻率約為主系統固有頻率的1/2時，自參數系統中存在著自參數內共振現象，即當外力的激振頻率接近主系統的固有頻率時，主系統會產生一個普通的共振，而主系統的共振會激發次系統的參數共振，這就是所謂的自參數內共振，自參數內共振是自參數振動中最危險的一種，可能給結構系統帶來災難性的后果。Xia等[11]研究了斜拉梁系統的自參數振動；陳丕華等[12]對斜拉索的面內參數振動進行了理論和試驗研究；王濤等[13]對大跨度鐵路斜拉橋索-梁的共振與參數共振問題進行了數值模擬分析；Li等[14-15]利用數值和試驗方法研究了框架結構的自參數共振問題。

現有研究主要集中在梁、殼體和斜拉索橋等結構，且多為平面內失穩。關于門式框架結構平面外的動力失穩(參數共振)問題的研究尚未見到相關文獻報道。本文擬采用試驗方法研究門式框架結構平面外的動力失穩問題，鑒于目前的參數振動試驗一般采用接觸式的激振器，約束了結構的位移，難以激發結構系統的內共振現象，本文將采用一種新型的非接觸式激振方法用于激發門式框架的自參數內共振，通過試驗分析門式框架結構出平面外的動態失穩的發生機理并探索其產生共振的不穩定區域，可為工程設計提供參考依據。

1 試驗研究

1.1 試驗模型設計

本試驗擬研究門式框架結構出平面外自參數內共振和非內共振兩種共振工況。試驗采用鉸接式門式框架(見圖1，坐標如圖1所示)，即門式框架橫梁的兩端與框架柱鉸接， 將門式框架橫梁視為主系統，兩個柱視為次系統。設門式框架的橫梁與柱的自振頻率分別為fHL與fSL，作用在橫梁中點上的周期荷載頻率為f，當f=2fSL，但fHL≠2fSL時，橫梁傳遞給柱的軸力頻率為柱彎曲振動頻率的二倍，這時柱將發生z方向自參數共振(為非內共振情形)；當f=fHL=2fSL時，外激勵荷載將激發橫梁的普通共振，由橫梁的普通共振導致柱在z方向的參數共振，此為內共振情形。

為研究平面外自參數共振特性，要保證主系統的受迫振動和其引起的次系統的參數共振不在同一平面內，本試驗設計了如圖1所示的門式框架結構模型，其中橫梁(以下簡稱HL)和兩個柱(以下簡稱SL)所在平面垂直。HL和SL采取鉸接方式，連接處用合頁連接，SL可沿HL的端部截面自由旋轉。SL的另一端通過夾具固定在剛性底板上，模擬固支邊界條件。選用不銹鋼作為模型材料，其密度為7 850 kg/m3，泊松比ν=0.3，彈性模量E=1.549×1011Pa。

自參數內共振和非內共振模型分別如圖1(a)及圖1(b)所示。在圖1(a)中為了保證HL局部(y方向)振動頻率fHL大致為SL出平面外(z方向)振動頻率fSL的兩倍，在HL中間設置了36 g的磁鐵作為集中質量進行調頻，可得fHL≈2fSL；在圖1(b)中為了使fHL≠2fSL，在兩個SL的頂部分別設置144 g的集中質量(磁鐵)調頻，可使fHL遠離2fSL。

1.2 試驗設備

本試驗的工作設備包括激振系統和數據采集系統兩個部分，試驗設備與模型示意圖如圖2所示，試驗設備照片如圖3所示。

1.2.1 激振系統

試驗的激勵信號由信號發生器(型號為：EM32003B)產生，該信號發生器有較高的數字調頻分辨率和頻率穩定度，主波形輸出頻率為1 μHz～5 MHz，擁有多種基本波形，本試驗中采用正弦波；正弦信號被發送給功率放大器(型號為：GF100)放大后，提供給激振器使電磁激振器產生激振力；為保證主系統振動時位移不受激勵裝置約束，本試驗中采用DJ-20型非接觸式電磁激振器對橫梁中點進行非接觸激振。本試驗中非接觸式的電磁力難以直接測量，本文可測量激振點處的位移，可將這個位移看成激勵位移，事實上可根據結構動力學原理，可將這個激勵位移轉化成等效的激勵力。

1.2.2 數據采集系統

試驗采用激光位移傳感器(型號為：HL-G112-S-J)進行測點的位移信號捕捉，位移信號由數據采集儀(型號為：INV306N)采集后傳輸至電腦，對應使用的數據處理軟件為Coinv DASP V10(以下簡稱DASP)，DASP是一個數據采集和信號處理軟件，具有波形、頻譜分析以及數字信號處理等多種功能，通過DASP可以實時觀測和記錄模型的振動位移數據。試驗中可同時測量橫梁中點y方向的位移(可看成位移激勵)及柱中點z方向的位移。

1.3 模態分析

開始試驗前需對模型結構進行模態分析，研究結構動力特性。本文采用ANSYS軟件進行理論模態分析和試驗模態分析結合的方式，對比驗證得到各模態的模態振型、固有頻率和阻尼比。

1.3.1 ANSYS計算模態

使用ANSYS建立模型，進行模態分析，自參數內共振模型和自參數非共振模型的分析結果如圖4和圖5所示， 兩個模型的一階振型均為出平面外(z方向)整體振動(實為柱的振動)，二階振型為橫梁上下(y方向)局部振動。對應的計算頻率如圖中所示。

1.3.2 試驗模態

用“自由衰減法”測定門式框架各部分的自振頻率及阻尼比系數，即在結構上施加一個初位移，使結構發生自由衰減振動。根據ANSYS計算的模態結果，分別對結構施加水平初位移和對HL施加豎向初位移測量一階、二階自振頻率及阻尼比系數。在HL和SL中點處放置激光位移計，記錄衰減振動位移時程曲線，對位移時程曲線進行FFT分析后，可得到的頻響函數曲線，在頻響函數曲線中讀取的振幅峰值對應的頻率即結構的自振頻率；根據衰減位移曲線可得到對應阻尼比系數，具體測量方法可參見2017年Li等的研究。經過五次測量，得到實測頻率的平均值，將兩模型的實測值與ANSYS計算的理論值列于表1和表2，可見頻率的實測值與理論值吻合度良好。

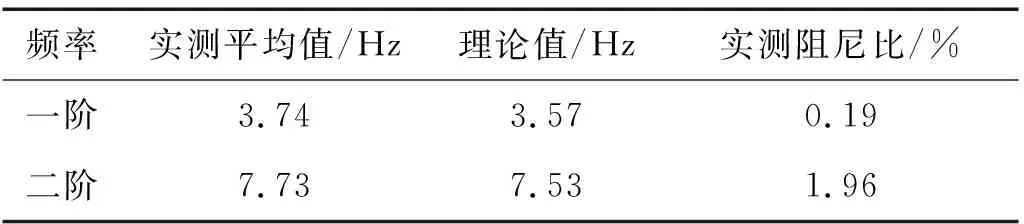
表1 自參數內共振模型自振頻率與阻尼比

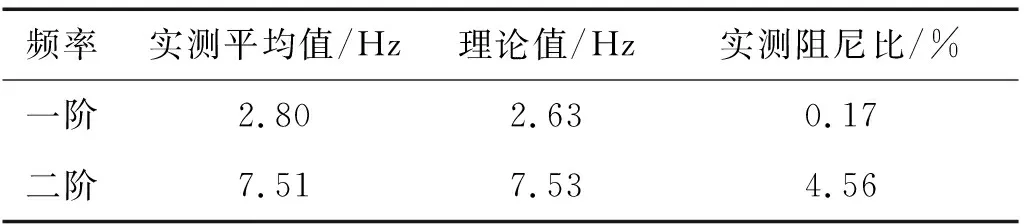
表2 自參數非內共振模型自振頻率與阻尼比

2 試驗結果

2.1 自參數內共振試驗

本模型中HL作為主系統，SL作為次系統，橫梁自振頻率比較接近二倍的柱自振頻率，即fHL≈2fSL。試驗時調節支架并固定電磁激振器，使激勵源正對橫梁中部，并在HL和SL的中點處分別放置激光位移計，記錄位移數據。根據頻率測量結果，設置激振頻率為f=7.50 Hz，即滿足f≈fHL≈2fSL，保持頻率不變，逐漸增大激勵，直到結構發生動力失穩，記錄下失穩的整個過程。圖6～圖8為模型動力失穩過程中HL和SL的位移時程曲線，因為HL的位移響應幅值在之后近似保持穩定在3.13 mm左右，此處僅展示0～15 s的曲線，并截取0～2 s曲線如圖7所示，從圖7可以明顯看到開始時HL的位移響應幅值在短時間內線性增長，為典型的普通共振曲線，表明HL在外部激勵作用下發生了普通共振，將共振的穩態激勵振幅3.13 mm(見圖7)可看成是SL參數共振的位移激勵幅值。圖8顯示在HL共振產生的位移激勵作用下，SL的位移響應非線性(指數)增長，在SL的位移時程曲線中截取30個周期，計算出SL的響應頻率為3.75 Hz，其響應頻率為激勵頻率f=7.50 Hz的一半，說明SL發生了主參數共振。且SL的位移響應增長經歷了較長一段時間，在57 s后幅值達到穩定，開始進行穩態運動，這種穩態運動稱為參數共振的“極限環運動”。整個自參數內共振失穩的過程可以見鏈接視頻https:∥www.bilibili.com/video/BV12A411g71w。

2.2 自參數非內共振試驗

與自參數內共振試驗相似，根據試驗測量結果，柱(一階)振動頻率fSL=2.80 Hz，設置激振器激勵頻率f=2fSL=5.60 Hz，得到的HL和SL的位移時程曲線分別如圖9和圖10所示，截取0～5 s內HL的位移時程曲線如圖9所示，得到HL響應頻率為5.60 Hz，說明HL在外激勵作用下受迫振動，其中HL振幅近似為5.54 mm作為SL振動的位移激勵。圖10顯示SL位移幅值非線性增長后達到穩定，進行穩定的“極限環運動”，其響應頻率為2.80 Hz，等于結構一階自振頻率，且為激勵頻率的一半，說明SL在HL位移激勵的作用下發生了主參數共振。該工況中結構發生動力失穩的全過程可見鏈接視頻https:∥www.bilibili.com/video/BV1J5411g7EE。

2.3 不穩定邊界測量和對比

根據非線性動力學的理論，當激勵頻率f在次系統自振頻率(fSL)2倍附近時，激勵位移大于失穩的激發值時，才會觸發結構的自參數共振，因此存在使得結構剛好失穩的臨界頻率-振幅，即不穩定邊界。為測量不穩定邊界，可以在2fSL附近設置掃頻區間，從低頻到高頻對結構逐次施加周期性激勵，對同一頻率的激勵，從小到大逐漸增加激勵幅值的大小，直到柱結構產生動力失穩。當激勵振幅較大時，動力失穩的現象十分明顯，柱會發生大幅劇烈振動，激勵頻率越接近2fSL，臨界激勵振幅越小。試驗中，觀察到柱振動幅值較大，且響應頻率與激勵頻率滿足1 ∶2的關系時，認為結構發生了自參數共振。

首先進行自參數內共振模型的不穩定邊界測量。已知fSL=3.74 Hz，因此設置掃頻區間為7.45 Hz～7.59 Hz，步長為0.01 Hz進行掃頻試驗，位移激勵的幅值按圖7的方式近似讀取。測得邊界上的激勵頻率f-激勵振幅A如表3所示，將得到的數據散點繪制成圖并進行曲線擬合，得到實測激勵頻率f-激勵振幅A的散點及擬合結果如圖11所示。

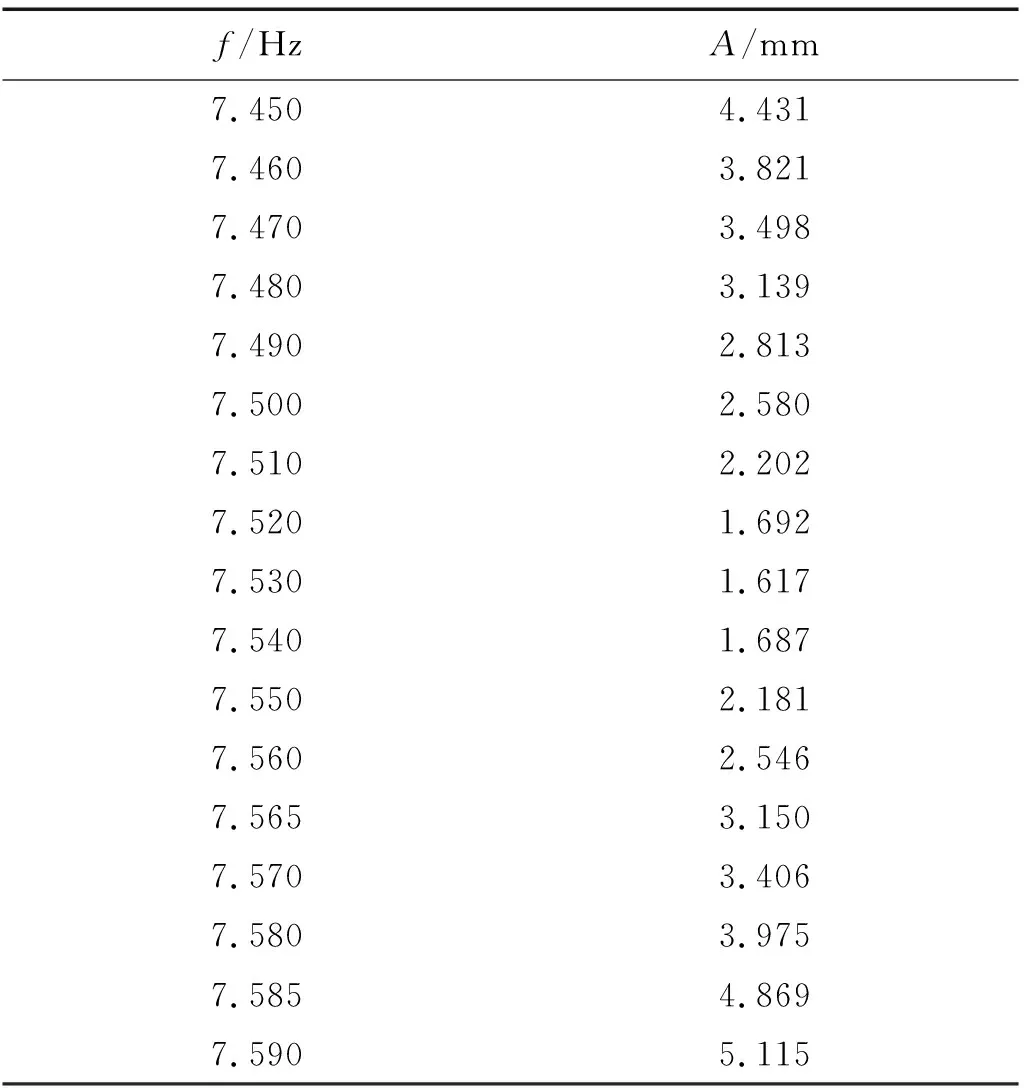
表3 內共振模型不穩定邊界測量結果

同理，對于自參數非內共振模型的不穩定邊界測量，已知fSL=2.80 Hz，設置掃頻區間5.55 Hz～5.65 Hz進行掃頻試驗，步長為0.01 Hz，測得的激勵頻率f-激勵振幅A如表4所示，并進行曲線擬合，得到實測激勵頻率f-激勵振幅A點及擬合結果如圖12所示。

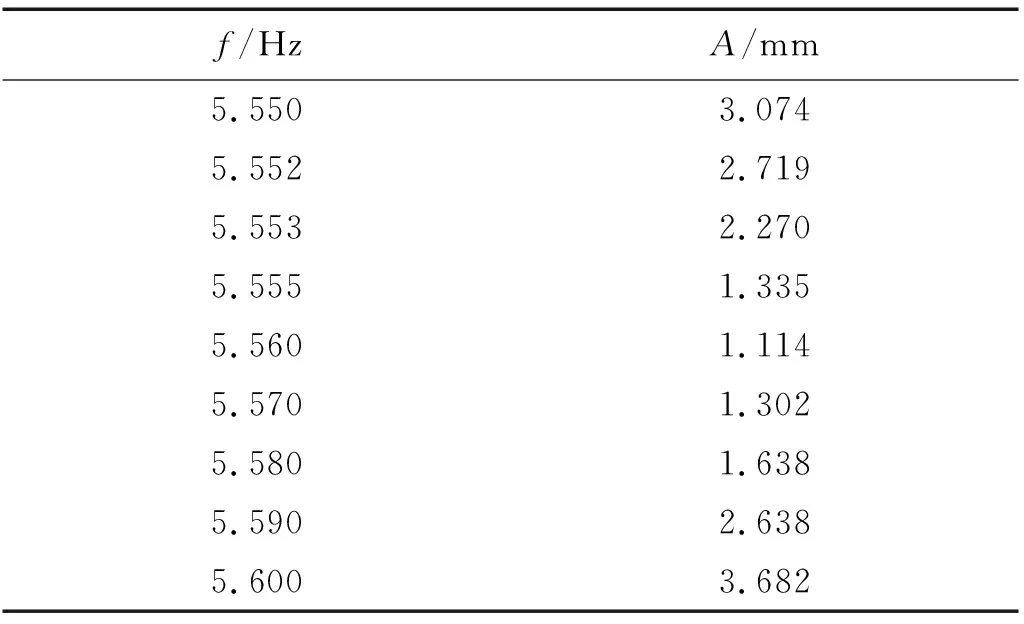
表4 非內共振不穩定邊界測量結果

對比圖11和圖12，自參數內共振的動力不穩定域明顯更寬，即在較大一段頻率區間內都可能發生動力失穩，實際上自參數內共振工況下的振幅是由HL共振引起的，所需外激勵力比非內共振(HL為一般的強迫振動)要小很多(這一問題的理論說明見2021年Li等的研究，此處不再贅述)，表明自參數內共振具有更大的危害性。

3 結 論

本文通過試驗的方法研究了(鉸接式)門式框架結構平面外動力失穩問題，分別對門式框架結構自參數內共振和非內共振模型進行了試驗分析。試驗結果表明:

(1)在門式框架結構中，在橫梁上施加相當于柱自振頻率兩倍的周期性激勵時，橫梁的振動會作為參數激勵引起柱在垂直于作用力的平面內發生主參數共振失穩，即發生自參數共振，且在自參數共振失穩后，柱位移響應呈非線性(指數)增長，最后趨向于“極限環運動”，振幅維持穩定。

(2)當門式框架發生自參數內共振時，橫梁發生普通共振，位移響應呈線性增長后穩定在某個值，這個值作為參數激勵能夠激發柱在垂直于外激勵的平面內發生主參數共振，且柱位移響應呈非線性(指數)增長，柱參數振動的增長滯后于橫梁普通共振的增長，說明參數共振存在能量積攢的過程。

(3)對比門式框架結構自參數內共振和非內共振的不穩定邊界，發現自參數內共振的動力不穩定區域更寬，即更易發生動力失穩。

自參數共振尤其是自參數內共振對門式框架結構的動力穩定性影響極大，在工程設計中應結合不穩定區域考慮在使用過程中結構是否存在失穩風險，并通過調整結構參數對其進行規避，減少門式框架結構動力失穩的發生。