金屬/陶瓷功能梯度懸臂板的振動抑制研究

呂書鋒， 李宏潔， 張 偉， 宋曉娟

(1. 內蒙古工業(yè)大學 力學系，呼和浩特 010051；2. 北京工業(yè)大學 材料與制造學部 機械結構非線性振動與強度北京市重點實驗室, 北京 100124；3. 內蒙古工業(yè)大學 機械工程學院，呼和浩特 010051)

航空航天領域中的很多結構都可以簡化為懸臂板模型，如飛機機翼、火箭翼和太陽能帆板等，在外部激勵作用下，這類結構極易發(fā)生由于振動導致的失穩(wěn)等問題，對飛行穩(wěn)定性和工作精度等造成重大影響。功能梯度材料(functionally graded material ，F(xiàn)GM)具有較高的強度和韌性，可作為飛行器的蒙皮材料以提高壁板結構的剛度，再結合有效的控制策略可以極大改善懸臂板結構的動力學穩(wěn)定性。因此，開展功能梯度懸臂板結構的動力學特性及振動抑制研究具有非常重要的理論和工程應用價值。許多學者已經(jīng)對FGM板殼的振動特性問題進行了研究。尹碩輝等[1]基于一階剪切變形板理論，采用等幾何有限元法，討論了體積分數(shù)指數(shù)、邊界條件及長厚比對金屬陶瓷功能梯度板自由振動頻率的影響。周鳳璽等[2]運用打靶法數(shù)值求解了功能梯度矩形板自由振動特性。Yang等[3-4]運用一維微分求積法、伽遼金法，分析了熱環(huán)境下初始應力功能梯度板的自由振動和強迫振動特性，以及在分布脈沖橫向荷載作用下初始應力功能梯度矩形薄板在彈性基礎上的動態(tài)響應。Huang等[5]基于高階剪切變形板理論，研究了帶有壓電層的功能梯度板在熱環(huán)境下的非線性振動和動力響應。Zhang等[6]采用Rayleigh-Ritz方法，分析了具有復雜邊界條件功能梯度矩形板的振動特性。Katili等[7]基于有限單元方法研究了功能梯度材料板的自由振動特性。Talha等[8]研究了功能梯度板的隨機振動特性。

在現(xiàn)有研究中，對抑制功能梯度材料板振動的研究大多集中在運用速度反饋控制器、機械載荷反饋控制器、LQR控制器、以及自適應模糊控制器等策略進行振動控制，采用魯棒控制器開展功能梯度懸臂板振動抑制的研究較少。由于建模方法、測量誤差或外部擾動影響，智能結構模型總會存在各種不確定性，這將會直接影響振動主動控制的效果，相比其他控制方法，魯棒控制可以在保證系統(tǒng)穩(wěn)定的條件下，控制系統(tǒng)對外部擾動具有相當大的穩(wěn)定裕度。因此本文運用魯棒控制策略，研究功能梯度懸臂板的振動抑制問題，其創(chuàng)新之處首先在于考慮了系統(tǒng)存在不確定性，其次是引入了全維狀態(tài)觀測器對魯棒控制策略進行改進，以達到抑制振動的作用。

1 功能梯度懸臂板的動力學方程

假設該懸臂板長為a，寬為b，厚為h。在板的上下表面分別貼有厚度為hp的壓電片，中間層的Ti-6Al-4V/Aluminum oxide(鈦合金/氧化鋁)沿厚度方向按體積分數(shù)冪律進行梯度分布。考慮氣動載荷作用下，附有作動器和傳感器的功能梯度懸臂板模型如圖1所示。

由于功能梯度板組成材料具有溫度依賴性，因此材料有效性能是關于溫度和坐標z的函數(shù)，具體表示為

Peff(T,z)=PM(T)VM(z)+PC(T)[1-VM(z)]

(1)

式中：Peff為功能梯度材料的有效性能；VM為Ti-6Al-4V的體積分數(shù)；PC和PM分別為Aluminum oxide和Ti-6Al-4V的熱物參數(shù)，隨溫度的變化規(guī)律為[24]

P=P0(P-1T-1+1+P1T+P2T2+P3T3)

(2)

式中，P0，P-1，P1，P2和P3為溫度相關系數(shù)。

VM符合冪率分布形式為

(3)

式中，n(0≤n≤∞)為體積分數(shù)指數(shù)，在體積分數(shù)指數(shù)不同的條件下，VM隨無量綱厚度的變化由圖2給出。

由圖2可以發(fā)現(xiàn)，隨著體積分數(shù)指數(shù)n的增加，Ti-6Al-4V的體積分數(shù)隨之下降。當n=0時，懸臂板由Ti-6Al-4V材料組成，而當n趨近于無窮時，懸臂板由Aluminum oxide材料組成。

應用經(jīng)典層合板理論構建功能梯度復合懸臂板位移場[25]

(4a)

(4b)

w(x,y,z,t)=w0(x,y,t)

(4c)

式中，u0，v0，w0為中面沿x，y，z坐標方向的任意點的位移分量。

FGM懸臂板的位移-應變關系可表示為

(5)

忽略結構的彎扭耦合效應，功能梯度懸臂板的本構方程可表示為

(6)

式中：Qij(z)(i，j=1，2，6)為功能梯度復合材料懸臂板的剛度矩陣；α11=α22=αf(T,z)為功能梯度復合材料懸臂板的熱膨脹系數(shù)；ΔT=T-T0為無熱應變T0的參考溫度的溫度增量。

在忽略熱效應和磁效應的情況下，給出壓電片的本構方程為

(7a)

Ei=-hklεk+βijDj

(7b)

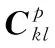
利用Hamilton原理推導功能梯度懸臂板的運動微分方程可表示為

(8)

式中：K為動能；U為勢能；δW為外力虛功。

功能梯度懸臂板的動能表示為

(9)

式中，I=ρh+2ρphp，ρ和ρp分別為功能梯度懸臂板和壓電片的密度。

FGM懸臂板的應力勢能具體表達式為

(10)

假設壓電作動器和傳感器是各向同性材料，具有相同的幾何參數(shù)。因此，將式(7)代入壓電片的應力勢能δUP表達式為[26]

(11)

氣動力作用下功能梯度懸臂板的虛功δw表示為[27-28]

(12)

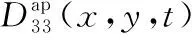
(13)

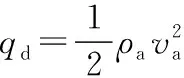
利用變分法，將式(9)～式(12)代入式(8)，可以得到以下5個表達式

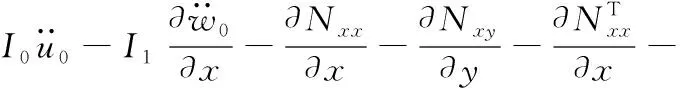
(14)

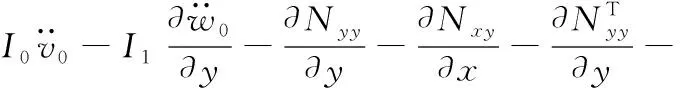
(15)

(16)

(17)

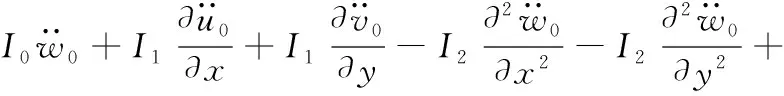
(18)

其中，

式中：上標a和ap均為壓電作動器；上標s和sp均為壓電傳感器。

考慮到結構以橫向振動為主，本文主要研究了功能梯度懸臂板的橫向線性振動，為方便求解控制方程，引入如下無量綱變量

(19)

當滿足懸臂板邊界條件下，給出如下二階橫向振動位移模態(tài)函數(shù)

w0=w1(t)X1(x)Y1(y)+w2(t)X2(x)Y2(y)

(20)

式中，w1(t)和w2(t)分別為一階和二階振動模態(tài)的無量綱幅值。

利用Galerkin方法，得到懸臂板的兩自由度運動控制方程

(21)

式中：M為系統(tǒng)的質量矩陣；Z為系統(tǒng)的阻尼矩陣；K為系統(tǒng)的剛度矩陣；F為系統(tǒng)外部載荷矩陣。

2 功能梯度懸臂板的主動振動控制

2.1 壓電傳感器的建模

壓電傳感器作為實際控制系統(tǒng)所需的重要元件，可為控制器提供與系統(tǒng)響應相關的控制信號，從而決定控制系統(tǒng)性能，因此有必要對壓電傳感器進行建模。

定義一個狀態(tài)變量X，表達式如下

(22)

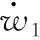
將懸臂板的兩自由度運動控制方程寫為狀態(tài)變量形式

(23)

式中，

式(23)描述了在輸入Va(t)作用下系統(tǒng)內部狀態(tài)的演化。同樣運用狀態(tài)變量X來描述系統(tǒng)輸出，即對壓電傳感器建模，則輸出方程

Y=[C]X

(24)

式中：Y為反饋信號；C為輸出系數(shù)矩陣。

2.2 魯棒控制器的設計

本節(jié)將設計魯棒控制器來抑制FGM懸臂板的振動。由于模型中機電耦合的復雜性，控制系統(tǒng)的參數(shù)一般存在一定的不確定性。因此，在設計控制系統(tǒng)時，有必要考慮參數(shù)不確定性的影響，則控制方程如下

(25)

Y=[C]X

(26)

式中，ΔA和ΔB為系統(tǒng)參數(shù)不確定部分，具體表達式如下

(27)

式中：M，E1和E2為具有適當維數(shù)的常數(shù)矩陣；G(t)為滿足以下條件的時變矩陣函數(shù)

G(t)TG(t)≤I

(28)

狀態(tài)反饋控制器如下所示

Va(t)=-KaX(t)

(29)

式中：X(t)為可測的狀態(tài)變量；Ka為狀態(tài)反饋控制器的反饋增益矩陣。

由于不可能測量所有的狀態(tài)變量，狀態(tài)反饋控制器的控制效率將受到影響，為此在反饋封閉系統(tǒng)中引入了全維狀態(tài)觀測器。全維狀態(tài)觀測器的表達式如下[29]

(30)

式中：X(t)0為觀測狀態(tài)變量；L為觀測器增益矩陣。

將全維狀態(tài)觀測器引入到狀態(tài)反饋控制器中，式(29)可以改寫為

Va(t)=-KaX(t)0

(31)

利用狀態(tài)矢量誤差矩陣e=X(t)-X(t)0，由式(25)、式(26)、式(30)得到閉環(huán)回路控制方程

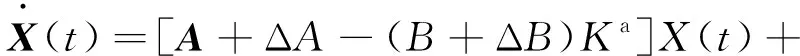
(32)

(33)

為實現(xiàn)對懸臂板振動的抑制，需求解式(32)、式(33)中的反饋增益矩陣與觀測增益矩陣，為此引入定理1進行求解。

定理1如果存在矩陣Mi(i=1, 2, 3 )，Ni(i=1, 2, 3 )和正定標量εi(i=1～5 )，且滿足下列矩陣不等式，則系統(tǒng)的控制方程是漸進穩(wěn)定的。

(34)

在設計控制系統(tǒng)時，總是需要保證系統(tǒng)是漸近穩(wěn)定。由于滿足定理1的條件等價于系統(tǒng)是漸近穩(wěn)定的，為此需要運用李雅普諾夫直接法結合引理1來證明該系統(tǒng)滿足定理1的條件，且趨于漸進穩(wěn)定。

證明利用反證法，假設振動控制系統(tǒng)是漸進穩(wěn)定的，構建一個標量函數(shù)，具體表示為

V=eTQe+XTPX

(35)

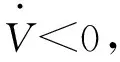
(36)

引理1對于合適維度的定常矩陣H與R，若有任意ε>0，那么下列不等式成立

(37)

將式(27)、式(32)以及式(33)分別代入式(36)，并利用引理1與式(28)，可以得到如下不等式矩陣方程

(38)

其中，

ξ=P(A-BKa)+(A-BKa)TP+

P[(ε3+ε5)MMT+ε4BBT]P+

(39)

將式(39)前后乘以P-1，利用Schur補引理，可得如下形式

(40)

證明完畢。

2.3 線性二次型最優(yōu)控制

LQR是一種最優(yōu)化控制方法。在最優(yōu)控制中，反饋控制系統(tǒng)的設計目的是為了使得與需要的系統(tǒng)響應成比例的性能指標最小化。從代數(shù)的角度來說，可定義響應的二次型作為性能指標，這樣將在很大程度上簡化最優(yōu)化問題。性能指標為

(41)

式中：Q為狀態(tài)變量的加權矩陣；R為輸入變量的加權矩陣。

結合式(23)、式(24),最優(yōu)控制的輸入表示為

U(t)=-GLX(t)

(42)

式中，GL為反饋增益矩陣，具體表達如下

GL=R-1BTλ(t)

(43)

式中，λ(t)為拉格朗日乘子矢量。

假設：

λ(t)=PX(t)

(44)

可以得到反饋增益矩陣GL=R-1BTP。其中，P為待定矩陣，滿足如下Riccati方程

PA+ATP-PBR-1BTP+CTQC=0

(45)

由于可能存在不完全可控的系統(tǒng)狀態(tài)，二次型性能指標函數(shù)無法達到最優(yōu)。因此需要驗證系統(tǒng)的可控性。所謂系統(tǒng)狀態(tài)完全可控或可控是指對于一個狀態(tài)變量X屬于n維實空間的線性定常系統(tǒng)，若在tf>t0有限的時間內，存在一個能在tf內使n維實空間任意狀態(tài)X(t0)轉移到X(tf)的控制輸入U(tf,t0)。系統(tǒng)狀態(tài)完全可控的條件是如下n維的可控矩Qc陣的秩為n

Qc=[BABA2B…An-1B]

(46)

3 算例分析

由Ti-6Al-4V/Aluminum oxide組成的FGM懸臂板，長為a=1 m，寬為b=1 m，板厚為h=0.004 m，壓電片厚為hp=0.1 mm。Aluminum oxide材料常數(shù)：ρ=3 750 kg/m3，其溫度相關系數(shù)如表1所示。Ti-6Al-4V材料常數(shù)：ρ=4 429 kg/m3其溫度相關系數(shù)如表2所示。G_1195N壓電作動器/傳感器材料常數(shù)為：Ep=63×109N/m2，ρp=7 600 kg/m3，νp=0.3，β33=6.667×107m/F，h31=h32=-39.37×108V/m，d31=d32=254×10-12m/V。

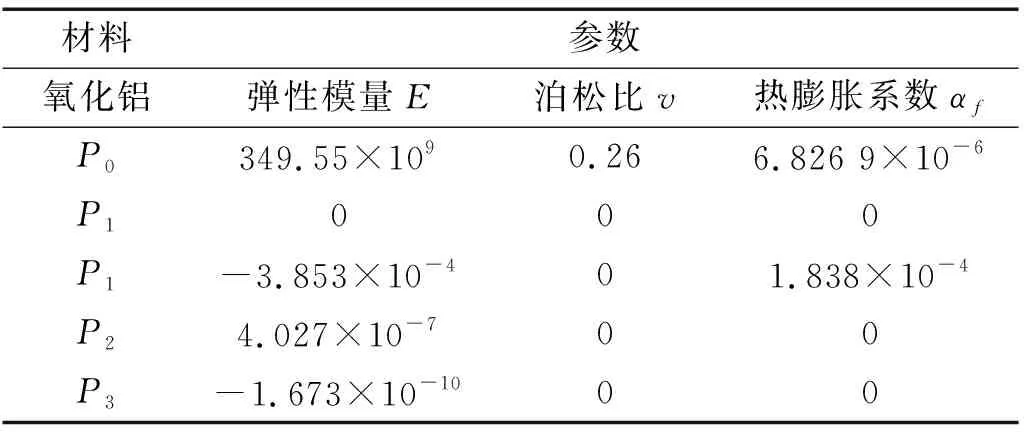
表1 Aluminum oxide的溫度相關系數(shù)

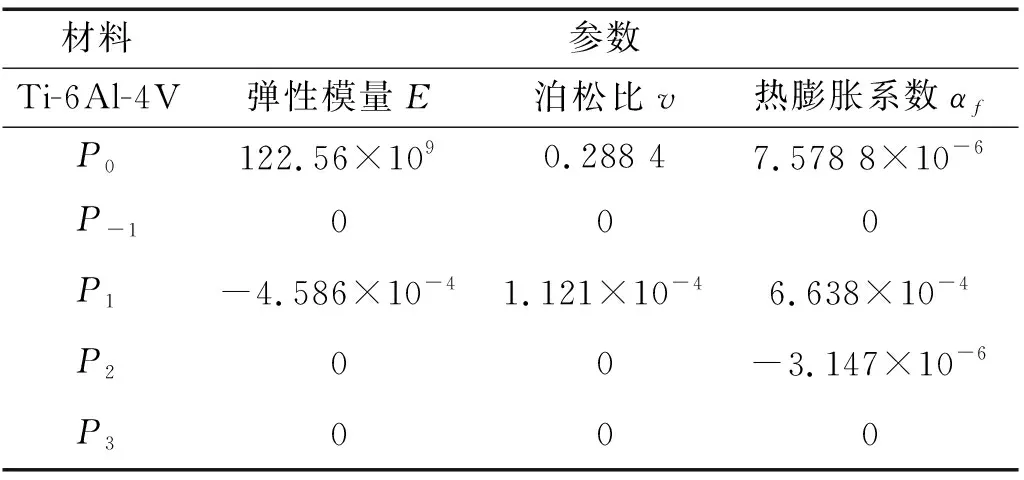
表2 Ti-6Al-4V的溫度相關系數(shù)

3.1 算例對比

在相同參數(shù)下，將含壓電層的FGM懸臂板與He等研究中的前兩階固有頻率進行了比較分析。板的長和寬均為0.4 m，厚度為5 mm，壓電片厚度為0.1 mm。懸臂板的前二階固有頻率如表3所示。由表3中可知，本文所得結果與He等的研究結果基本一致。

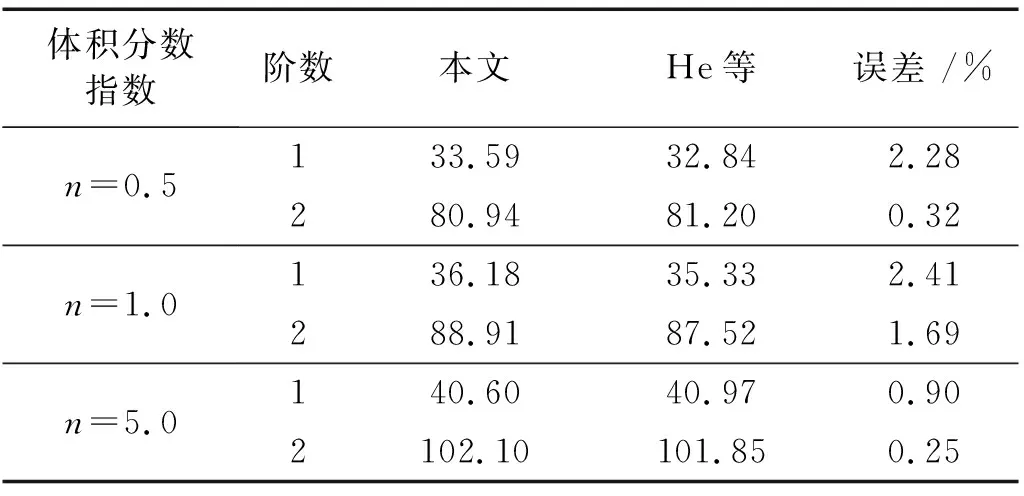
表3 功能梯度懸臂板一階與二階固有頻率

3.2 不同參數(shù)對懸臂固有頻率的影響

本節(jié)采用數(shù)值方法研究體積分數(shù)指數(shù)和長寬比等不同參數(shù)對FGM懸臂板動力學特性的影響。表4給出了不同體積分數(shù)指數(shù)和長寬比下的FGM懸臂板前兩階無量綱固有頻率值。

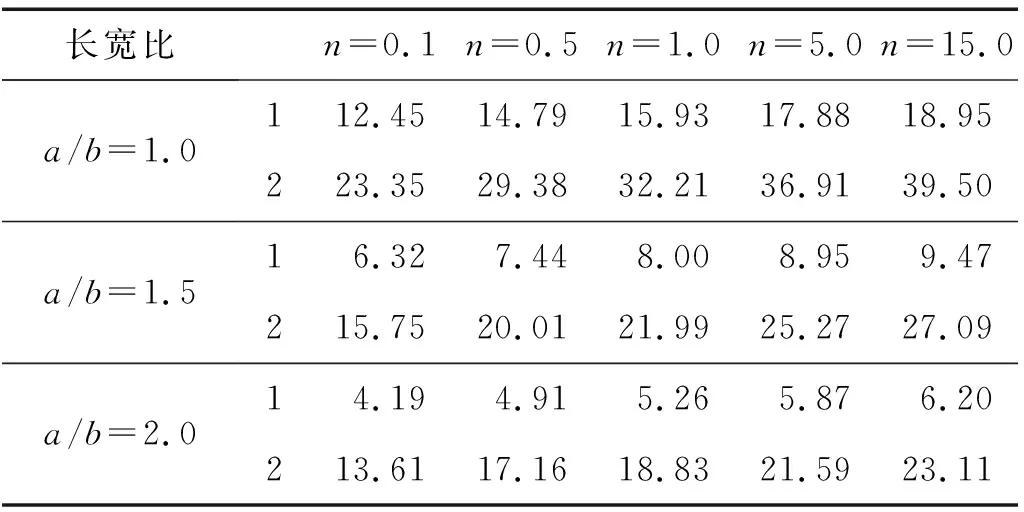
表4 不同體積分數(shù)指數(shù)和長寬比下FGM懸臂板無量綱固有頻率

從表4可以得出，對于不同的體積分數(shù)指數(shù)下，F(xiàn)GM懸臂板的一階與二階無量綱固有頻率隨體積分數(shù)指數(shù)的增加而增大。這是由于隨著體積分數(shù)指數(shù)n增大，Aluminum oxide體積分數(shù)增高，故懸臂板剛度不斷增大，進而FGM懸臂板的一階與二階固有頻率增加。在同質量情況下，三種不同的長寬比(a/b=1.0,a/b=1.5和a/b=2.0)，板的一階與二階無量綱固有頻率隨長寬比的增加而減小，這是因為隨著長寬比的增加，結構的剛度減小，進而造成板的固有頻率降低。

3.3 不同參數(shù)下控制器的有效性

本節(jié)在參數(shù)不同的條件下，驗證魯棒控制器的有效性。圖3和圖4分別給出了長寬比a/b=1.0，體積分數(shù)指數(shù)n=0.5,n=1.0和n=5.0時，功能梯度懸臂板振動控制前后的一階無量綱時間歷程圖和在兩種控制器下的控制電壓圖。

從圖3可以看出，當體積分數(shù)指數(shù)為n=0.5,n=1.0和n=5.0，所設計的魯棒控制與LQR相比，系統(tǒng)衰減到穩(wěn)定狀態(tài)所需時間相對較長，控制效果相對較弱。但相比于控制前的一階模態(tài)的無量綱振動幅值，施加控制策略后的無量綱振動幅值在經(jīng)過一段時間后均呈衰減趨勢，直至收斂為零。

從圖4可以看出，所設計的魯棒控制器的控制電壓比LQR的控制電壓小，即控制作用的成本相對較小，整個控制過程中所消耗的能量相對較低。原因在于采用LQR控制的系統(tǒng)衰減到穩(wěn)定狀態(tài)所用的時間短，但是這是以犧牲控制電壓為代價的，從而增加控制成本。

綜合圖3和圖4可以得出，在不同體積分數(shù)指數(shù)下，所設計的控制器能夠有效地抑制FGM懸臂板在氣動力下的振動幅值。

圖5和圖6分別給出了體積分數(shù)指數(shù)n=5，長寬比a/b=0.75，a/b=1.00和a/b=1.50時，功能梯度懸臂板振動控制前后的一階無量綱時間歷程圖和在兩種控制器下的控制電壓圖。

從圖5和圖6可以看出，當長寬比為a/b=0.75,a/b=1.00和a/b=1.50時，所設計的魯棒控制與LQR相比，控制響應的速率相對較慢，控制效果相對較弱，但所需的輸入控制電壓相對較小，即控制過程所耗能量相對較低。且相比于控制前一階模態(tài)的無量綱振動幅值，施加控制策略后的無量綱振動幅值在經(jīng)過一段時間后均呈現(xiàn)收斂趨勢，直至收斂為零。即改變結構長寬比，所設計的控制器仍可以有效地抑制FGM懸臂板在氣動力下的振動幅值。

FGM材料溫度相關性在FGM板振動問題中起重要作用，因此，有必要討論溫度變化的影響。圖7和圖8分別給出了當體積分數(shù)指數(shù)n=5，溫度T=300 K，T=400 K和T=500 K情況下，控制前后功能梯度懸臂板一階無量綱時間歷程圖和在兩種控制器下的控制電壓圖。

從圖7和圖8可以看出，在溫度參數(shù)不同的情況下，所設計的控制器相較于LQR，其控制效果較弱但所需要的輸入控制電壓較少。應用控制策略后的無量綱振幅均呈遞減趨勢至趨近于零，由此可見，考慮溫度影響時，所設計的控制器可以有效地抑制FGM懸臂板在氣動力下的振動幅值。

3.4 材料參數(shù)不確定下控制器的有效性

本節(jié)在考慮材料參數(shù)不確定情況下，驗證所設計控制器的有效性。假設功能梯度懸臂板與壓電層的材料參數(shù)值有一定的偏差，其中壓電材料的密度ρp、彈性模量Ep和功能梯度懸臂板的彈性模量E1，E2，剪切模量G12均為原材料參數(shù)值的90%。

圖9和圖10分別給出了材料參數(shù)不確定情況下功能梯度懸臂板一階無量綱時間歷程圖，以及在兩種控制器下的控制電壓圖。

從圖9和圖10可以看出，當材料參數(shù)不確定時，與原系統(tǒng)相比，施加控制魯棒策略后，系統(tǒng)達到穩(wěn)定的時間變長，控制速率降低，需要的輸入控制電壓逐漸減少，系統(tǒng)的控制效果明顯減弱，無量綱振幅仍呈衰減趨勢，最終收斂至零。而施加LQR后，控制電壓無變化，控制器失效。因此，在材料參數(shù)不確定情況下，當前設計的魯棒控制器可以抑制功能梯度懸臂板的振動。

4 結 論

本文提出了一種抑制金屬/陶瓷功能梯度懸臂板振動的魯棒控制方法。運用Hamilton原理和Galerkin方法，推導出功能梯度懸臂板受氣動力作用的動力學方程，研究了體積分數(shù)指數(shù)和長寬比對FGM懸臂板振動特性的影響。算例分析表明，隨著體積分數(shù)指數(shù)的增加，功能梯度懸臂板的一階與二階無量綱固有頻率增大。當改變結構幾何參數(shù)時，功能梯度懸臂板的一階與二階無量綱固有頻率隨著板長寬比的增大而減小。

基于得到的動力學方程，構造全維狀態(tài)觀測器，設計魯棒控制器，形成控制系統(tǒng)閉合回路，從而達到抑制FGM懸臂板振動的目的。在控制策略上，引入LQR，并分析兩種控制器的控制效率。同時通過比較施加控制策略前后懸臂板的一階無量綱時間歷程圖，發(fā)現(xiàn)所提出的控制器在不同體積分數(shù)指數(shù)、長寬比、溫度以及材料參數(shù)不確定情況下均能有效抑制結構振動幅值。且所設計的魯棒控制器的控制電壓比LQR的控制電壓小，即控制作用的成本相對較小，整個控制過程中所消耗的能量相對較低。