基于被動引射的大擴張比噴管流動數值研究

吳超，黃興

中國航發湖南動力機械研究所，湖南 株洲 412002

噴管是發動機主要的部件之一，其方案設計對于吸氣式發動機的性能有著重大的影響[1-3]。隨著飛行高度增加，環境壓力減小，為實現最佳性能，噴管達到臨界工作狀態時的擴張比也增加。在大擴張比噴管地面試驗過程中，過膨脹會造成高溫燃氣在噴管內的分離流動現象，從而對試車結果的評定、結構傳熱等產生影響，嚴重時可能對噴管和發動機結構造成破壞[3-4]，因此受到廣泛的關注和研究。

針對噴管流動分離問題，國內外開展了大量的研究。對分離流動的模型進行了分析，通過試驗和仿真表明了存在兩種流動模式[5-8]。胡海峰[9]等采用數值方法詳細研究了噴管流動中出現氣流分離模態的變化情況，并對大擴張比噴管流動特性與噴管結構耦合的氣動彈性問題進行了分析；王一白[10]針對拋物線噴管研究了型面參數對流動分離模態轉換的影響；王曉輝[11]開展了固體火箭發動機噴管分離流動及其數值模擬研究，分析了噴管在不同入口總壓情況下的流場參數分布；周文清[12]為研究氣流分離對噴管性能的影響，開展了理論計算與數值模擬分析，獲得了分離點位置及推力系數的變化；賈睿東[13]對超聲速噴管中激波分離誘發流場對稱破缺的機理進行了深入研究，并提出控制方法。這些研究工作對大擴張比噴管的分離流動進行了全面深入的分析，為噴管設計及地面試驗提供了參考。

為避免大擴張比噴管地面試驗中分離流動帶來的不利影響，通常需要在高空臺下開展試驗[14]。但高空模試車臺系統復雜，受發動機尺寸影響，費用昂貴且時間周期長，對于試驗條件提出了較高的要求。引射技術是一種在流體流動控制中常用的技術，其在高空臺設計中也得到了應用[15]，但是研究相對較少，且在高空臺中的實現過程較為復雜。

針對大擴張比噴管地面試驗中的分離流動問題，本文開展了基于簡單幾何結構引射筒進行流動控制的研究，基于數值建模方法，研究了分離流場的參數分布規律，在此基礎上針對引射方案，分析了不同參數對流場的影響，研究基于被動引射方案實現地面試驗過程中噴管滿流工作的可行性，為地面試驗提供一種分離抑制的技術途徑。

1 計算模型

1.1 幾何模型及計算條件

以軸對稱噴管為研究對象，噴管包含收縮段、喉道和擴張段，壁面型線由圓弧及相切的幾何關系組成，擴張比為45.2。

被動引射方案主要由噴管和引射筒組成，引射筒為等直徑圓筒，直徑略大于噴管出口截面直徑，前緣與噴管出口截面齊平，兩者幾何位置關系如圖1 所示。圖1 中，A 為噴管進口，B為對稱軸，C為壁面，D為出口邊界。噴管主要設計參數和計算條件見表1。

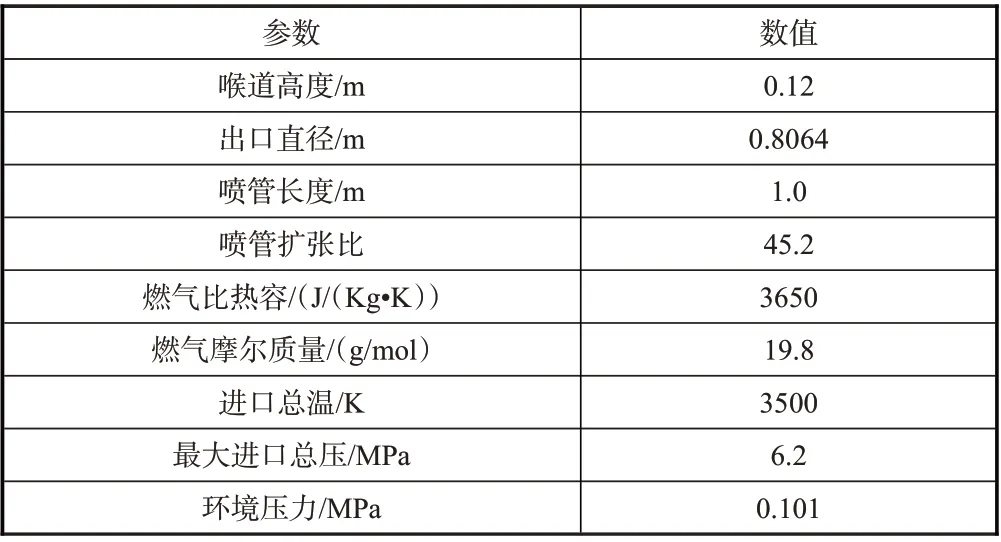
表1 計算參數Table 1 Calculation parameters

1.2 網格劃分及邊界條件

根據噴管的流動特點，過膨脹時在較高的反壓作用下會產生流動分離，近壁面邊界層區域網格對于分離點的預測十分關鍵。建模過程中，對近壁面區域網格進行加密，第一層網格Y+約為1。根據分離流場特點，會在中心區域形成馬赫盤，對對稱軸區域網格也進行加密。由于噴管和引射筒幾何模型相對簡單，流場全部生成結構化網格，共約42萬。

計算模型的主要邊界條件包括4類，如圖1中所示。噴管進口為壓力進口邊界，指定進口燃氣的總溫和總壓值，由于流動為亞聲速，靜壓只作為初始條件，數值與總壓一致。實際工作過程中發動機的壓力是隨時間變化的，采用UDF函數指定進口壓力隨時間的變化關系，模擬壓力建立過程。數值計算時間步長0.01s，共計算800 時間步。計算模型的幾何對稱軸為對稱軸邊界條件，噴管壁面、引射筒壁面均為壁面邊界條件，無需指定參數。計算過程中，外部區域邊界為壓力出口邊界，模擬環境大氣參數，給出壓力和溫度值。

1.3 控制方程與數值解法

流場控制方程為微分形式的N-S方程。在噴管流動仿真中，燃氣和空氣的物性參數有很大的差別，組分模擬計算時，通過求解第i種組分的對流擴散方程預測每一種組分的局部質量分數Yi

式中，Ri是第i種組分的生成率，Si是在此條件下控制方程中用戶自定義的源相導致的附加生成率，噴管流動過程中，燃氣與空氣不產生化學反應，僅計算組分擴散過程。

湍流條件下，質量擴散按照式（2）計算

式中，Sct為湍流施密特數；Di,m為第i中物質的擴散系數。

氣體黏性由Sutherland公式計算，采用三系數方程

式中，μ為氣體黏性；T為靜溫；μ0和T0分別為黏性和溫度的參考值；S為常數。

基于有限體積法，采用與時間相關的耦合隱式解法求解控制方程。對控制方程中的擴散項和對流項分別采用二階中心差分格式和二階迎風格式離散。湍流模型對于分離流動的預測十分關鍵。根據文獻研究選擇S-A 模型，以更好地計算逆壓梯度下的分離流動[9]。

1.4 分離位置經驗公式

試驗結果表明，當噴管出口壓力（壓強）與環境大氣壓力比大于0.3時，噴管中燃氣流動正常；當此比值小于0.3～0.4時，噴管中將出現激波分離現象。過膨脹噴管中是否出現分離可以用式（4）進行判斷[16]

式中，pi為分離點壓力；pa為環境壓力；而pc則為燃燒室壓力。

2 仿真計算與分析

2.1 噴管流場分析

針對典型工況進行數值計算，分析噴管在不同的進口壓力下的流動特征。圖2 和圖3 分別給出了進口壓力1.3MPa 和6.2MPa 不同工況下的流場馬赫數及燃氣組分分布。可以看到，兩種工況下噴管中均產生了分離流動和馬赫盤。高溫燃氣經過喉道后加速到超聲速狀態壓力不斷降低，外界環境壓力相對較高。根據激波理論，噴管出口截面的壓力理論值分別為1041Pa 和4964Pa，遠低于環境壓力。在較大的逆壓梯度下，燃氣從壁面附近邊界層開始分離，并向上游傳播，產生了曲面的激波流動現象。激波分為內外兩層，內激波中心主流在對稱軸附近產生了由正激波組成的馬赫盤，而外激波氣流向中心匯聚，并沿著馬赫盤外側流動。兩個不同工況下的流動特征相似，但是隨著進口壓力的提高，在環境壓力不變的前提下，分離點和馬赫盤的位置均向噴管出口移動，與之對應，噴管中流動最大馬赫數也提高。

對應于馬赫數分布，由圖3燃氣組分分布規律來看，分離區域從進口發展而來，氣體組分以空氣為主。在大范圍的分離區域，空氣將燃氣流“壓制”在中心區域。在空氣和燃氣之間，存在相互擴散的過渡區域，隨著與分離點距離的增加，擴散邊界越來越寬。

2.2 分離位置計算

針對不同進口壓力條件進行計算和分析，將噴管壁面分離區域壓力進行對比，如圖4所示。可以看到，噴管進口壓力變化對于分離點的位置具有決定性的影響。進口壓力越低，燃氣通過噴管喉道擴張流動過程中壓力下降越快，氣流更容易從壁面分離。在最小壓力點后壁面壓力迅速上升，此后壓力值緩慢上升，直至在噴管出口位置與環境壓力接近。隨著進口壓力的提升，分離點不斷向出口方向移動，最小壓力點的位置也后移。另外，通過曲線對比可以發現，壓力曲線在前半段的下降速率大，不同進口條件下壁面壓力最低值基本相同，分離區域壓力曲線平直，數值接近環境壓力。

將數值計算的分離位置對應的擴張比ξ計算結果，與按照式（4）計算的結果進行對比（見圖5），可見數值計算的分離點擴張比變化規律與經驗公式一致，隨著進口壓力p增加，分離點擴張比ξ增大，曲線進行呈現線性變化的特點。在較低的壓力下，兩個計算結果的曲線一致性較好；當壓力增大到4MPa以后，數值計算結果略低于經驗公式的數值，但最大誤差在10%以內。上述結果對比表明，本文數值模型能夠較好預測建模方法的可行性。

2.3 引射參數影響及流場分析

噴管流場計算結果表明，由于按照高空使用要求設計的噴管擴張比大，地面試驗時，即使在最大工作壓力下，噴管仍然處于過膨脹工作狀態，噴管內產生了分離流動。為此，開展了通過被動引射實現噴管內正常流動的可行性研究。在被動引射方案中，引射筒的長度Li和直徑Di是主要的幾何參數，作為影響流場的主要參數加以研究，計算過程中噴管進口壓力均取值6.2MPa。

（1）引射筒長度Li的影響

從圖6的馬赫數分布圖來看，隨著引射筒長度增加，對噴管的引射作用增強，流場的參數分布和噴管內流動過程也發生變化。與無引射筒馬赫數分布對比，當引射筒長度為0.5m時，兩者之間相似，燃氣在噴管的中后部開始分離，在對稱軸附近產生了明顯的馬赫盤，噴管未達到滿流狀態，但是分離位置向出口方向移動，馬赫盤的位置xi也明顯向后移動。

當引射筒長度為1.0m時，壁面分離區位置已經靠近噴管出口，基本可以保證噴管的滿流工作狀態，消除了壁面分離現象。此時，第一級馬赫盤繼續向后移動。隨著長度進一步增加，在引射筒內燃氣逐漸變成緊靠筒壁的貼壁流動，經過一段距離后，燃氣從引射筒壁面分離。與分離位置的變化相對應，隨著引射筒長度Li增加，噴管中心區域形成的馬赫盤也向后移動，尤其是引射筒長度為2.0m 時，相對于其他狀態而言，明顯的特征是馬赫盤基本消失。

根據計算結果，將第一級馬赫盤位置xi隨引射筒長度Li的變化關系進行對比，如圖7所示。可以看到，兩者之間近似呈拋物線關系。隨著馬赫盤向后移動，噴管流場的最大流動速度有所增加，但變化量較小。根據計算，引射筒長度Li由0 增加到2m 時，噴管流動最大速度由Ma4.16 增加到Ma4.38。

圖8給出了長度2.0m工況下引射筒前端局部區域流場速度及流線變化。此時噴管內流動達到滿流狀態，從噴管中噴出的高速氣流與引射筒壁面存在一定夾角，在等直徑的引射筒前端產生了一道內收縮激波，激波后氣流流線偏轉到水平方向并在引射筒內流動。在高速低壓燃氣流摩擦和剪切作用下，外部空氣通過引射筒與噴管出口之間的間隙進入引射筒內，并沿著筒壁向后流動。在筒內逆壓梯度作用下，經過一段距離燃氣流從引射筒壁面分離后向中心匯聚，并產生一道弱斜激波，氣流流線向中心偏轉，同時誘導分離區產生逆時針的回流現象。此工況下引射筒的中心區域基本沒有產生馬赫盤。

表2中對比了不同引射長度下流經引射筒與噴管出口間隙的流量。可以看到，隨著引射筒長度的增加，通過間隙的流量也增加，但兩者之間為非線性關系。引射筒長度超過1m后，流量增加的趨勢減緩，長度為1.5m和2.0m時噴管均為滿流狀態，間隙區域的流場參數已基本保持不變，引射筒內的分離區未影響到縫隙流動，此時引射流量也不變。

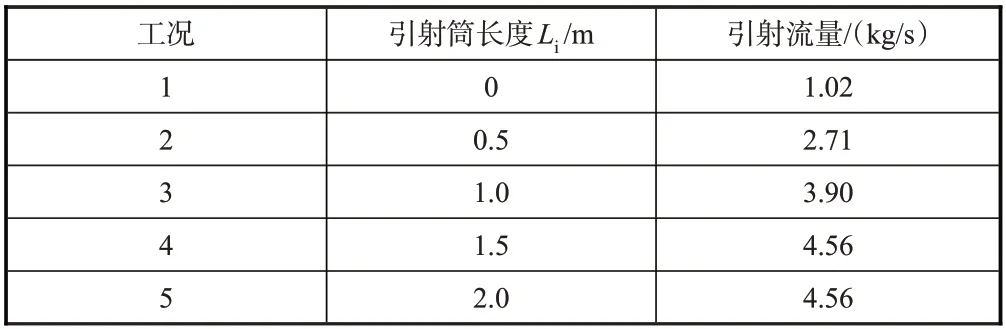
表2 不同引射長度下經過縫隙的流量對比Table 2 Comparison between flow through gap under different ejection lengths

（2）引射筒直徑Di的影響

直徑Di的變化改變了引射筒和噴管出口位置的間隙，對引射的流場和通過縫隙的流量產生影響，從而可能對流場產生影響，需要對此加以分析。

針對噴管進口壓力6.2MPa的狀態，固定引射筒長度為2m，分別對引射筒直徑0.8264m、0.8464m 和0.8664m 三種工況的流場進行分析。

對比圖9 中的流場參數變化，三種工況下均可保證噴管內的滿流工作狀態，引射筒直徑的不同對流場的影響主要表現在引射筒內。當引射筒直徑為0.8264m 時，對應的間隙高度為10mm，流場中消除了馬赫盤流動現象。直徑為0.8464m 時，間隙為20mm，流場馬赫數分布與間隙為10mm時基本一致，但引射筒的分離位置略向前移動，中心區域的馬赫盤尺寸很小。間隙進一步增加到30mm（直徑為0.8664m）時，引射筒內燃氣已經不能貼壁流動，而是發展到噴管的出口截面位置，氣流從噴管出口處就開始向中心匯聚。與此同時，馬赫盤的位置朝向噴管進口方向移動，且間隙為30mm時中心馬赫盤已經十分明顯。

從表3 的流量來看，引射筒直徑對于馬赫盤的位置有一定的影響，間隙越大則馬赫盤的位置越向前移動。與之對應，隨著間隙的增加，引射流量顯著增大。從數值上看，間隙為300mm 時的流量是間隙為10mm 時流量的3.09 倍，兩者之間接近線性關系。

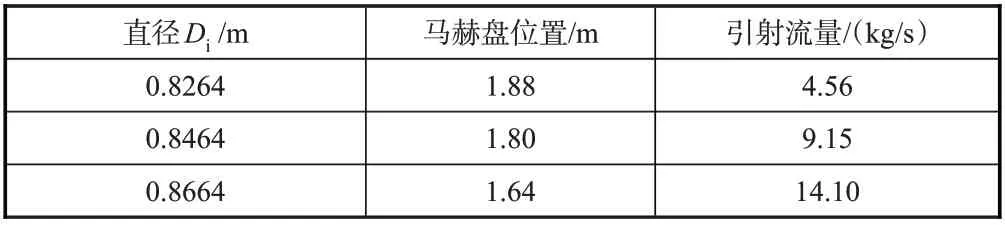
表3 不同引射筒直徑下引射流量Table 3 Ejection flow under different ejector cylinder diameters

3 結論

本文針對大擴張比噴管地面工作過程中，由于過膨脹而產生的局部分離流動問題，建立了基于等直引射筒的被動引射方案數值仿真模型，開展了不同引射筒長度和直徑下的流場參數計算，并對計算結果進行分析，得出以下結論：

（1）基于本文建立的數值仿真模型，可以較好地計算大擴張比噴管流動狀態及預測分離流動現象，仿真計算與經驗公式計算分離點結果較為接近，表明建模方法可行。

（2）引射筒的長度對引射效果和流場參數分布有重大影響。針對進口壓力6.2MPa的工況計算結果表明，當引射筒長度達到1.0m 以上時，可以實現噴管的滿流工作狀態，消除噴管內分離流動現象。

（3）增加引射筒的直徑，會增加通過引射筒和噴管間隙的引射流量，同時造成馬赫盤前移。在給定的典型工況下，直徑增加間隙增大到30mm時還可保證噴管的滿流工作狀態，相對于間隙10mm 的工況，出現了明顯的馬赫盤，且引分離位置前移到引射筒前端，引射效果下降。

本文的研究表明，增加引射筒長度和減小引射筒與噴管出口的間隙，有利于實現噴管的滿流工作狀態。通過合理控制引射筒尺寸參數，可以實現對大擴張比噴管地面試驗時過膨脹產生的分離流動現象的抑制，被動引射是一種可行的技術途徑。