在小學數學教學中滲透分類思想例談
——以“數學廣角——搭配（二）”教學為例

哈爾濱市花園小學 孫 寧

數學課要使學生真正理解和掌握基本的數學知識與技能、數學思想與方法，得到必要的數學思維訓練，獲得廣泛的數學活動經驗。小學數學課堂一項重要的內容就是數學思想方法的滲透，而分類思想又是其中尤為重要的思想方法之一。教學中滲透分類思想，不僅可以培養學生有順序地、有層次地、全面有邏輯性地思考，還能培養學生良好的數學思維品質。從知識的層面而言，發展分類思想能讓學生由淺入深不斷地分類學習，既要把握全局，又能細致入微，形成系統的認知結構。

以三年級下冊“數學廣角——搭配（二）”例1的教學為例，研究如何在教學中有效滲透分類思想，讓學生在類比、分析、概括中實現對分類思想的運用。

1.教學目標

（1）掌握排列兩位數的簡單方法，會用四個數字組成沒有重復數字的兩位數。

（2）經歷探索簡單事物排列規律的過程，體會分類思想，培養有序思考的習慣，提升觀察推理的能力。

（3）感受數學與生活的緊密聯系，激發學生學好數學的信心，培養學生從數學的角度看待周圍事物，提升全面思考問題的意識。

2.設計理念

借助問題情境、新舊知識聯結、自主探究式學習促進學生思考交流，用畫圖列表等方式直觀呈現解決問題的方法，在思維碰撞中不斷感受提升，將學生思維引向深處，逐步掌握有序、全面思考問題的方法。

3.上掛下聯

教材中這部分內容是在二年級上冊“數學廣角”的基礎上進行學習的，學生已初步接觸了一些簡單的排列和組合內容，初步感受了排列組合的思想和方法。本單元的例1教學，引導學生嘗試稍復雜的排列，這里的例題不僅排列的數字多了1個，而且還增加了“0”這個特殊的數字，體現思維的有序性和全面性，滲透分類思想。

4.教學活動

（1）復習舊知，引入新課

師：前面我們學習過簡單的數字組合，你們還記得嗎？課前老師要考考你們，請想一想用1、3、5 這三個數字能組成多少個沒有重復數字的兩位數？

生：可以組成的兩位數有13、15、31、35、51、53 六個數字。

師：你們是怎么做到準確又沒有遺漏呢？

生：可以先確定十位上的數字，個位上的數字逐一替換，如十位上是1，個位可以是3或5，組成的兩位數是13和15。

師：同學們真不簡單，把幾個數字進行有序排列，就能產生不同的數字，今天我們繼續來研究有關數字組合的問題。（板書課題：數學廣角搭配例1）

數學是有結構的，有系統的，更是有機的整體，復雜的知識中一定會有內在聯系。例1的內容對學生來說還是比較抽象，距離二年級的學習也間隔較遠，此時學生解決這類問題的經驗和方法，依然停留在二年級具體操作的層面上。因此整節課在導入部分，教師有意識地從二年級數字排列問題入手，引導學生回顧舊知，用1、3、5 這三個數字組成沒有重復的兩位數。在這樣的活動中喚醒學生已有認知，找到學生學習最近發展區，從而為數學排列中有0的問題做鋪墊。

（2）自主探索，合作交流

活動一：展示排列，體會有序

出示例1：用數字0、1、3、5能組成多少個沒有重復數字的兩位數？把你想到的數字寫下來。

（學生自主嘗試，教師巡視。）

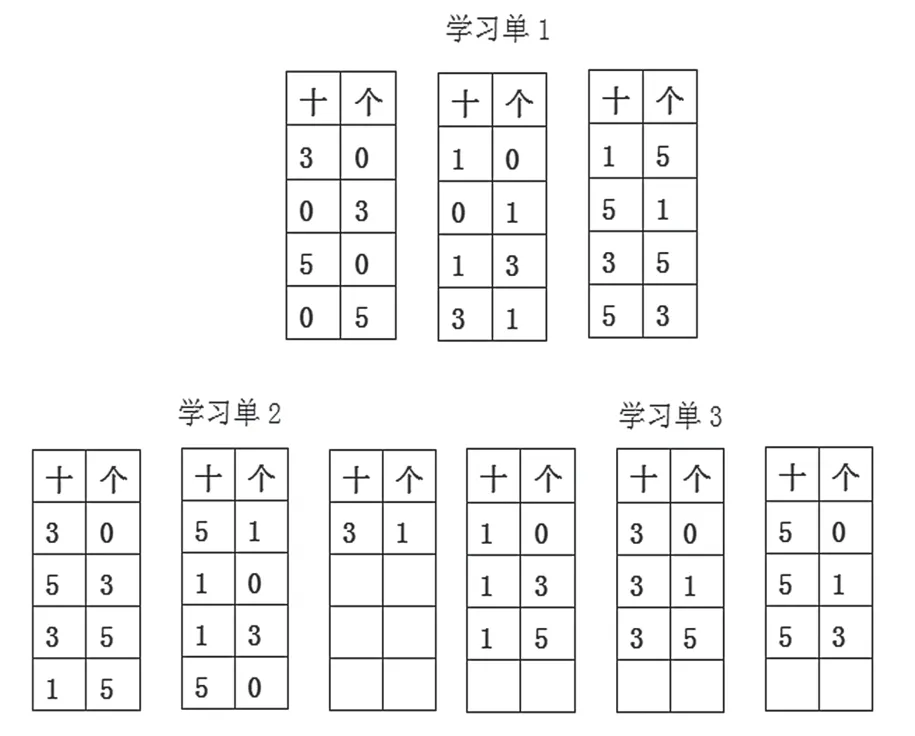
師：我在同學們的作品中找到了幾個有代表性的，我們來看一看，請同學們觀察下面的學習單，說說你有什么發現？

生：學習單1 是錯誤的排列，因為0 不能在十位。

生：學習單2 雖然出現的兩位數都對，但是缺少順序，容易遺漏。

生：學習單3 的排列有順序，用固定十位的方法組成了9個兩位數，有順序、不重復、不遺漏。

師：剛才大家一直說在排列的過程中要有順序不遺漏，具體應該怎么做呢？

生：先固定個位，然后依次進行排列。個位是0，然后十位就可以是 1、3、5，兩位數就有 10、30、50；個位是 1，符合條件的兩位數有31、51；個位是3，符合條件的兩位數有13、53；個位是 5 ，符合條件的兩位數是 15、35，共 9 個兩位數。

生：先固定十位，然后依次進行排列。如十位上是1，個位可以是 0、3、5，兩位數就有 10、13、15；十位是 3 ，符合條件的兩位數有30、31、35；十位是5，符合條件的兩位數有50、51、53，一共9 個兩位數。這樣出現的數字還能保證從小到大的排列。

師：看來為了使我們的思考更加有序，我們可以固定某一位，十位或個位，使另外的幾個數字按照從小到大的順序依次進行搭配，做到有序思考、不重復不遺漏，同時還要關注十位上不能出現0。（板書：有序思考 不重復不遺漏）

通過任務單提供學習性支架，引導學生在實踐中發現排列的多種可能。通過學習單的展示，發現問題，引發學生更加關注有序思考的重要性。

活動二：觀察對比找策略

師：用數字1、3、7、9能組成多少個沒有重復數字的兩位數？請你在學習單上寫一寫。

（學生獨立嘗試，教師搜集學情。）

匯報：他們的方法你看懂了嗎？請你說一說。

展示不同學情，全班進行交流。

生：先固定個位，然后將剩下的數字放到十位上，依次進行排列。個位是1，然后十位就可以是3、7和9；個位是3，符合條件的兩位數有 13、73、93；個位是 7，符合條件的兩位數有17、37、97；個位是9，符合條件的兩位數是19、39、79，共 12 個兩位數。

生：先固定十位，然后將剩下的數字放到個位上，依次進行排列。十位是1，然后個位就可以是3、7和9；十位是3，符合條件的兩位數有31、37、39；當十位是7的時候，找出的兩位數有71、73和79；當十位數是9的時候，找出的兩位數是 91、93、97，共 12個兩位數。

追問：兩種方法看似不同，但思考的本質是相同的。都是先固定一個數位上的數字，再按順序排列另幾個數。你更喜歡哪一種方法呢？請結合著你自己的理解適當修改完善你的學習單，然后把你排列的方法跟同桌說一說。（同桌再次交流方法。）

師：對比這兩次活動，要求相同，為什么結果不同呢？

生：0 是一個特殊的數字，0 不能在十位出現，所以十位上只能是 1、3、5。所以用 0、1、3、5 只能組成 9 個沒有重復數字的兩位數。

師：確實0 的出現讓我們看到了新的問題，在有0的排列中我們首先要思考0不能在十位，然后再用固定數位的方法依次進行搭配，做到有序思考、不重復、不遺漏。（板書：0不能在十位）

本環節教師借助有梯度的學習活動，引導學生的思維活動逐步走向深入，從而掌握有序、全面思考問題的方法。設計中的兩個重要活動，都是用不同的數字組成兩位數，然而在教學目的和層次上又是不同的。在活動一中，先讓學生自主嘗試解決例1的問題，在交流對比中發現問題，體會有序思考的必要性，進而探究有序思考的方法。在活動二中，引導學生運用所學策略，嘗試有序思考解決問題，同時在兩次活動的比較中，發現4個數字中有0的情況。通過活動二的再次對比，借助直觀表格，呈現數字排列規律，運用數形結合思想，引導學生形成正向遷移提煉方法策略，促進思維發展。

（3）鞏固練習，提升運用

基礎練習 ：“做一做”第 1 題：用 0、3、5、7 可以組成多少個沒有重復數字的兩位數？

變式練習：“做一做”第2題：把5 塊巧克力全部分給小麗、小明、小紅，每人至少分一塊，有幾種分法？

拓展練習：用 1、3、5、8 組成沒有重復的兩位數，組成多少個個位是單數的兩位數？

數學思想方法是數學的靈魂，它反映著數學知識的本質與核心價值。練習中教師精心設計有梯度的習題應用，關注基礎知識和基本技能的理解與掌握。強化有0 的數字搭配，進一步鞏固本節課的學習方法，引導學生在解決問題中反復感悟、體驗領悟分類的數學思想。

從上面的教學中，我們不難發現要讓學生掌握一種思想方法，就要先充分了解學情，找到學生最近發展區，挖掘教材把握教學契機，設計符合學情的活動。分類思想要逐類逐級討論，適時為學生提供學習支架，幫學生建立新舊知識之間的聯系，讓學生體會到現在所學內容，就是在以往的知識和方法上又添了一些新情況而已，滲透分類思想。讓學生在類比中發現和總結新的方法，逐漸完善知識的整體結構，體會分類思想在解決問題中的作用。