統(tǒng)計分析理論在大學(xué)生學(xué)習(xí)成績分析中的應(yīng)用
江志冬
(福州大學(xué)至誠學(xué)院經(jīng)濟管理系,福建 福州 350002)
0 引言
現(xiàn)階段,各高等院校正著力推進本科教育內(nèi)涵式發(fā)展[1],本科生培養(yǎng)質(zhì)量是教育部門、高等院校關(guān)注的重點.大學(xué)生的學(xué)習(xí)成績是檢驗課程學(xué)習(xí)成果的重要指標(biāo),作為高等院校的教務(wù)部門不能僅僅關(guān)注學(xué)習(xí)成績的及格率,更應(yīng)該分析隱藏在這些成績背后的現(xiàn)象,為提高教學(xué)質(zhì)量奠定基礎(chǔ).何韻竹等采用數(shù)據(jù)挖掘算法分析了大學(xué)生成績,研究發(fā)現(xiàn)計算機網(wǎng)絡(luò)、操作系統(tǒng)及英語是影響軟件工程專業(yè)學(xué)生能否獲得獎學(xué)金的重要科目[2];黃蕙等采用關(guān)聯(lián)規(guī)則方法研究學(xué)生成績,建議教務(wù)管理部門根據(jù)關(guān)聯(lián)規(guī)則分析結(jié)果調(diào)整排課順序,提升教學(xué)效率[3];賈連廣等采用相關(guān)性檢驗發(fā)現(xiàn)線性代數(shù)成績與高等數(shù)學(xué)成績具有很強的相關(guān)性,建議對線性代數(shù)成績不高的學(xué)生應(yīng)多加指導(dǎo),以便更好地學(xué)習(xí)高等數(shù)學(xué)[4].此外,大學(xué)生成績分析的常用方法還有決策樹算法、聚類方法、回歸分析方法、主成分分析方法等.
通過以上分析可知,許多學(xué)者正嘗試用統(tǒng)計學(xué)理論、數(shù)據(jù)挖掘技術(shù)、機器學(xué)習(xí)方法等研究大學(xué)生成績,并取得了良好成果.大部分教務(wù)管理人員采用Excel對成績進行分析,但計算步驟較為繁瑣;而如果采用數(shù)據(jù)挖掘技術(shù)、機器學(xué)習(xí)方法,則要求教務(wù)管理人員掌握數(shù)據(jù)分析技術(shù).基于此,本文結(jié)合成績分析的總體思路,采用常用的統(tǒng)計分析方法對學(xué)生學(xué)習(xí)成績進行分析,并以某學(xué)院A專業(yè)學(xué)生學(xué)習(xí)成績?yōu)槔M行實證研究.
1 學(xué)習(xí)成績分析思路
首先,確定分析對象并導(dǎo)出學(xué)習(xí)成績,必要時對數(shù)據(jù)進行清洗,確保分析數(shù)據(jù)的準(zhǔn)確性;其次,采用描述統(tǒng)計方法對成績進行描述統(tǒng)計分析,計算課程成績的及格率,對于成績及格率較低的課程,考查其成績結(jié)構(gòu)分布情況;再次,采用差異分析方法研究成績在性別、班級等方面的差異,采用相關(guān)性分析方法研究課程成績的相關(guān)性;最后,根據(jù)成績分析結(jié)果提出教學(xué)優(yōu)化措施.
2 統(tǒng)計分析方法
本文采用的統(tǒng)計分析方法有兩獨立樣本T檢驗、單因素方差分析、Mann-Whitney U檢驗、多獨立樣本Kruskal-Wallis檢驗和皮爾遜相關(guān)性分析.
(1)兩獨立樣本T檢驗.該方法利用來自兩個獨立總體的樣本推斷兩個總體的均值是否存在顯著性差異,使用的前提是兩個樣本相互獨立,并且樣本來自的總體應(yīng)服從或者近似服從正態(tài)分布.
(2)單因素方差分析.該方法用于檢驗兩個以上總體的均值是否相等,要求數(shù)據(jù)服從或者近似服從正態(tài)分布.當(dāng)總體存在差異時,可采用多重比較技術(shù)分析各組之間的均值是否存在顯著性差異.
(3)Mann-Whitney U檢驗.該方法是一種雙獨立樣本的非參數(shù)檢驗方法,兩組的觀測值被合并,而后賦予秩,如果秩和檢驗的差值較大,可認(rèn)為兩個樣本來自不同分布[5].
(4)多獨立樣本Kruskal-Wallis檢驗.該方法用于檢驗多個(兩個以上)總體的分布是否存在顯著差異,是一種非參數(shù)統(tǒng)計方法,適用于數(shù)據(jù)呈非正態(tài)分布的情況[6].
(5)皮爾遜相關(guān)性分析.皮爾遜相關(guān)系數(shù)可用于度量兩個變量之間線性相關(guān)性的密切程度及方向.如果計算得到的P值小于給定顯著水平a(一般默認(rèn)為0.05),表明變量之間存在顯著的線性相關(guān)關(guān)系,否則認(rèn)為變量之間不存在顯著的線性相關(guān)關(guān)系.
3 實證分析
3.1 數(shù)據(jù)來源
以某學(xué)院A專業(yè)148名學(xué)生學(xué)習(xí)成績作為數(shù)據(jù)來源.該學(xué)院為地方普通本科高校,A專業(yè)的人才培養(yǎng)目標(biāo)為基礎(chǔ)扎實、適應(yīng)面寬、應(yīng)用能力強的高級應(yīng)用型人才.分析數(shù)據(jù)為A專業(yè)某個年級大一學(xué)年通過正常考試獲得的成績(不包含補考、重修).
3.2 結(jié)果與分析
3.2.1 課程成績描述統(tǒng)計分析
對各門課程成績進行描述統(tǒng)計分析,整理結(jié)果如表1所示.軍事訓(xùn)練是大一新生的必修課程,通過該門課程則成績記為60分;體育成績包含早晨、晚上的體育鍛煉成績,如未通過規(guī)定 測 試則記0分.結(jié)合極差、標(biāo)準(zhǔn)差統(tǒng)計量可發(fā)現(xiàn)學(xué)生成績差異較大,高數(shù)是及格率最低的科目.
3.2.2 及格率較低科目成績結(jié)構(gòu)分析
高數(shù)(上)的及格率為84.82%,高數(shù)(下)的及格率只有67.86%,說明下降幅度較大.究其原因,是由于高數(shù)(下)是高數(shù)(上)的延續(xù),難度系數(shù)會有所增加,對于高數(shù)(上)沒通過的學(xué)生而言,學(xué)習(xí)難度更是會劇增;而且,平均成績排名靠前的學(xué)生也出現(xiàn)了高數(shù)(下)不及格的情況,如某學(xué)生上學(xué)期平均分位列第12名(位列年級前10.7%),但卻出現(xiàn)高數(shù)(下)不及格的現(xiàn)象.通過進一步分析還發(fā)現(xiàn),高分段人數(shù)較少,主要集中在60~70分;從分布結(jié)果上看,數(shù)據(jù)呈負(fù)偏態(tài)分布,說明學(xué)生成績受到試卷結(jié)構(gòu)的影響.
線性代數(shù)的及格率為75%,高分段學(xué)生的人數(shù)較為正常,但低分段學(xué)生的人數(shù)偏多.通過進一步分析發(fā)現(xiàn),學(xué)生學(xué)習(xí)水平的差異很大.
3.2.3 成績在不同維度的差異分析
學(xué)生某一學(xué)期各門課程的平均分是衡量該學(xué)生學(xué)業(yè)水平的重要指標(biāo),其計算以課程的學(xué)分為權(quán)重.從及格率的分析可以看出,大學(xué)英語(上)、計算機(上)、高數(shù)(上)、高數(shù)(下)、線性代數(shù)、微觀經(jīng)濟學(xué)、大學(xué)英語(下)和計算機(下)的及格率具有較大的提升空間,因此以下重點分析這8門課程的平均分在性別、班級維度上的差異.在進行差異分析前,采用單樣本K-S檢驗方法判斷8門課程的成績是否服從正態(tài)分布.經(jīng)過檢驗發(fā)現(xiàn),當(dāng)顯著性水平為0.05時,計算機(上)、線性代數(shù)、大一上平均分、大一下平均分近似服從正態(tài)分布,其余成績均不服從正態(tài)分布.
3.2.3.1 成績在性別維度上的差異分析
對服從正態(tài)分布的成績采用兩獨立樣本T檢驗,對不服從正態(tài)分布的成績采用Mann-Whitney U檢驗,分析成績在性別維度上是否存在差異.
兩獨立樣本T檢驗結(jié)果見表2.從表2可以看出,當(dāng)顯著性水平為0.05時,可認(rèn)為計算機(上)成績在性別維度上不存在顯著性差異;女生線性代數(shù)成績顯著高于男生;大一上平均分女生顯著高于男生,但是大一下平均分在性別上不存在顯著性差異.

表2 兩獨立樣本T檢驗結(jié)果
表3顯示的是Mann-Whitney U檢驗結(jié)果,采用中位數(shù)度量不服從正態(tài)分布的成績水平.由表3可見,在顯著性水平為0.05時,可認(rèn)為女生的大學(xué)英語(上)成績顯著高于男生,其他成績不存在顯著性差異.
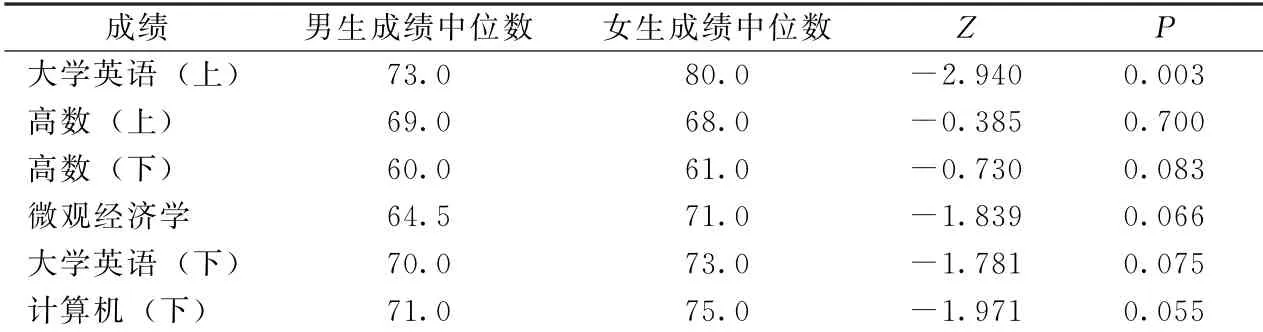
表3 Mann-Whitney U檢驗結(jié)果
3.2.3.2 成績在班級維度上的差異分析
本次分析的A專業(yè)有3個班級,因此對服從正態(tài)分布的成績采用單因素方差分析,對不服從正態(tài)分布的成績采用多獨立樣本Kruskal-Wallis檢驗,分析成績在班級維度上是否存在差異.
單因素方差分析結(jié)果如表4(12頁)所示.由表4可見,當(dāng)顯著性水平為0.05時,可認(rèn)為計算機(上)成績、線性代數(shù)成績在不同班級不存在顯著性差異;大一上平均分、大一下平均分在不同班級存在顯著性差異.進一步采用多重比較技術(shù)可以發(fā)現(xiàn),1班大一上平均分、大一下平均分顯著高于其他兩個班級.

表4 單因素方差分析結(jié)果
表5顯示的是多獨立樣本Kruskal-Wallis檢驗結(jié)果.由表5可見,當(dāng)顯著性水平為0.05時,可認(rèn)為高數(shù)(上)成績在班級維度上存在顯著性差異,采用中位數(shù)度量成績水平可發(fā)現(xiàn),1班的高數(shù)(上)成績顯著高于2班、3班,其他成績在班級維度上不存在顯著性差異.
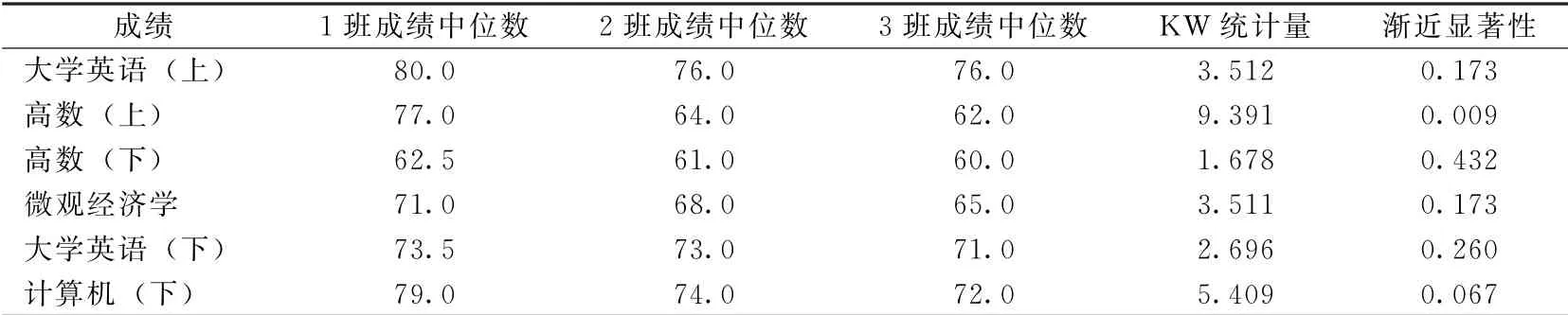
表5 Kruskal-Wallis檢驗結(jié)果
所選取的A專業(yè)3個班級中,學(xué)生的劃分是隨機的,而且3個班級的學(xué)生高考成績沒有顯著差異.經(jīng)過一學(xué)年的學(xué)習(xí),總體來看,1班的成績優(yōu)于其他兩個班級.根據(jù)后續(xù)的調(diào)查及座談發(fā)現(xiàn),1班的班委更為團結(jié),注重加強班級學(xué)風(fēng)建設(shè),學(xué)習(xí)氛圍良好,這也是影響班級總體成績的重要因素.
3.2.4 課程成績的相關(guān)性分析
采用皮爾遜相關(guān)性分析研究高數(shù)(上)成績與高數(shù)(下)成績和線性代數(shù)成績的相關(guān)性,課程間的相關(guān)性分析結(jié)果如表6所示.由表6可見,當(dāng)顯著性水平為0.05時,可認(rèn)為高數(shù)(上)成績與高數(shù)(下)成績、線性代數(shù)成績存在顯著正線性相關(guān)關(guān)系.因此,對高數(shù)(上)不及格或者分?jǐn)?shù)較低的學(xué)生要加強輔導(dǎo),從而有利于學(xué)生學(xué)好高數(shù)(下)和線性代數(shù)課程.

表6 課程間的相關(guān)性分析
4 結(jié)論
利用常用的統(tǒng)計分析方法對某學(xué)院A專業(yè)學(xué)生的學(xué)習(xí)成績進行實證研究,得到以下研究結(jié)果:(1)數(shù)學(xué)類課程的及格率偏低;(2)部分課程成績在性別維度上存在顯著性差異,班級學(xué)習(xí)氛圍是影響學(xué)習(xí)成績的重要因素;(3)從相關(guān)性分析角度看,高數(shù)(上)成績與高數(shù)(下)成績、線性代數(shù)成績存在顯著正線性相關(guān)關(guān)系.可見,采用統(tǒng)計分析方法能夠識別成績分布情況,分析成績在性別、班級維度上的差異,以及測算課程成績的相關(guān)關(guān)系.
基于以上分析結(jié)果,該專業(yè)教學(xué)活動可從以下方面進行優(yōu)化:(1)提高學(xué)生對數(shù)學(xué)類課程的學(xué)習(xí)興趣,可從多方面、多角度展示數(shù)學(xué)的重要性,培養(yǎng)學(xué)生數(shù)學(xué)思維,同時開展多樣化的輔導(dǎo)活動,加強對數(shù)學(xué)底子較弱學(xué)生的輔導(dǎo);(2)營造良好的班級學(xué)習(xí)氣氛,建立定期查課制度、隨堂聽課制度、學(xué)風(fēng)督查通報制度,促使學(xué)生養(yǎng)成自主學(xué)習(xí)的良好習(xí)慣,以利于提升學(xué)習(xí)成績;(3)重視數(shù)學(xué)類前置課程的學(xué)習(xí),專業(yè)負(fù)責(zé)人應(yīng)向?qū)W生闡述前置課程與后置課程之間的內(nèi)在關(guān)系,引導(dǎo)學(xué)生重視前置課程的學(xué)習(xí),要重點關(guān)注前置課程掛科的學(xué)生.
本文嘗試采用統(tǒng)計分析方法對大學(xué)生成績進行分析,為大學(xué)生成績分析提供了可借鑒的路徑.下一步,可增加成績樣本量,如分析多屆學(xué)生同一門課程學(xué)習(xí)成績的差異,分析學(xué)生在參加社團活動、擔(dān)任班干部等情況下學(xué)習(xí)成績的差異,從而拓展統(tǒng)計分析理論在大學(xué)生成績分析領(lǐng)域的應(yīng)用范圍.

