基于3D-MUSIC和波疊加的聲場重建方法*

孫玲莉 楊 超 郭 輝 胡定玉 顧汝彬

（1.上海工程技術大學機械與汽車工程學院 上海 201600）（2.上海工程技術大學城市軌道交通學院 上海 201600）（3.中國人民解放軍32128部隊 濟南 250000）

1 引言

近場聲全息（Near-filed Acoustic Holography，NAH）作為一種聲源定位和聲場可視化技術，可為振動、噪聲源分析提供豐富的聲源和聲場信息，對噪聲源控制及聲輻射研究具有重要價值。近場聲全息技術包含多種實現方法［1～4］，其中，波疊加法對各類聲場的適應性較好，且不用處理復雜積分問題，而得到廣泛運用。如：楊殿閣等［5］提出動態波疊加法計算運動聲源的聲場；Bai等［6］將粒子濾波算法與波疊加法相結合，提出從正向求解等效源源強；為減少空間采樣點數，Bi等［7］提出一種壓縮模態等效點源法，Hu等［8］在壓縮感知框架下對等效源法進行了改進。

利用波疊加法重建聲場，其計算精度取決于對等效源強度的求解，這屬于聲學逆問題，需采用正則化進行求解，已提出多種較為成熟的解決方法［9～10］。除此之外，等效源點的布置對等效源強度的求解起重要作用，影響波疊加法重建聲場的精度。李加慶等［11］提出利用波束形成進行聲源定位，指導等效源配置，再用波疊加法重建聲場。該方法是已知聲源與測量面的距離，在二維平面上進行聲源定位，對于聲源空間位置完全未知的情況，重建精度會受到影響。楊超等［12］提出用統計最優近場聲全息兩次定位聲源二維平面的位置，再通過三角函數定理求解聲源z軸距離，實現聲源的三維定位，再配置等效源。為進一步提高重建精度，Yang等［13］提出多次轉動全息面進行聲源三維定位，獲得足夠多的聲源位置信息，用卡爾曼濾波提高聲源定位精度。該方法將多種算法聯合，提高了波疊加法重建聲場的精度，但其計算分析較復雜，在實際應用中受到一定限制。

針對上述問題，提出一種基于3D-MUSIC算法和波疊加法的局部聲場重建方法。3D-MUSIC算法通過空間譜矩陣的求解及譜峰搜索，獲得聲源的俯仰角、方位角和距離等空間位置數據，可直接準確定位聲源的三維位置。根據3D-MUSIC算法搜索的位置信息，確定等效源的配置策略，利用波疊加法重建聲場。

2 理論基礎

2.1 3D-MUSIC算法

MUSIC算法是一種基于子空間特征分解的高分辨率譜估計算法，根據信號子空間和噪聲子空間的正交特性，構造出空間譜矩陣，通過空間譜矩陣的求解及譜峰搜索估計出信號的DOA參數。但經典MUSIC算法［14］僅適用于二維遠場聲源定位。改進的3D-MUSIC算法［15～16］可計算近場噪聲源的俯仰角、方位角和距離，實現聲源的三維空間定位。

如圖1所示，假設坐標原點o為參考點，任一聲源sd與參考點o的連線在xoy平面的投影oc與x軸的夾角θd為方位角，聲源sd與參考點o的連線與z軸的夾角ψd為俯仰角，rd為聲源sd到參考點o的距離，rmd為第m個傳聲器到聲源sd的距離。

圖1 傳聲器陣列接收信號示意

假設空間有D個近場窄帶信號源(s1(t)，…，sD(t))，輻射到由M個傳聲器組成的陣列上，第m個傳聲器接收到的信號表達式為

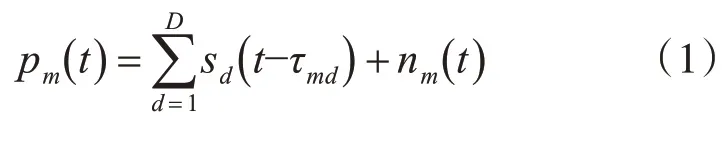
其中，d=1，2，…，D，m=1，2，…，M，nm(t)表示第m個傳聲器在t時刻接收到的高斯白噪聲。整個傳聲器陣列的接收信號表達式為

式中，S(t)為聲源，A是陣列方向矢量，N(t)是高斯白噪聲。其中：

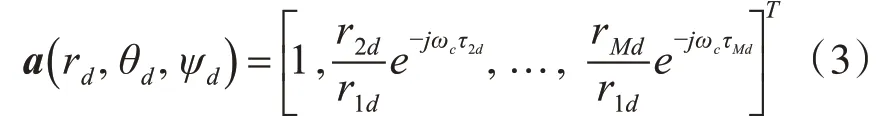
由圖1的幾何關系可知：

其中，rmd代表第m個傳聲器與第d個聲源與的距離；ωc為聲源的中心角頻率；τmd為第m個傳聲器接收到第d個聲源信號的相對時延。

對傳聲器陣列接收到的數據進行協方差運算，根據信號和噪聲互相獨立的特性，協方差矩陣可以將信號和噪聲分離。定義測量聲壓P(t)的協方差矩陣R(t)為

式中，ARs(t)AH為信號部分，σ2I為噪聲部分，Rs(t)為原始信號的協方差矩陣。對R(t)進行特征分解可得：

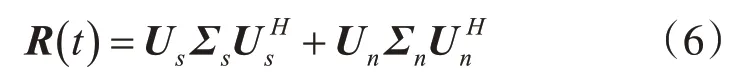
式中，Us為信號子空間，Un為噪聲子空間。由噪聲子空間與信號子空間相互正交可得：

構造空間譜函數為

3D-MUSIC算法對空間譜函數進行網格搜索，進而輸出空間譜函數為極大值的ψ，θ，r值，即空間聲源信號的俯仰角、方位角和距離。根據該聲源定位信息指導等效源的配置，進而利用波疊加法重建聲場。

2.2 波疊加算法

波疊加法的基本思想是將聲源輻射聲場用聲源內部分布的一系列等效源產生的聲場疊加替代，由全息面測得聲壓反求出等效源的強度，從而實現整個聲場的重建與預測。其中聲源面、重建面和全息面的位置關系如圖2所示。

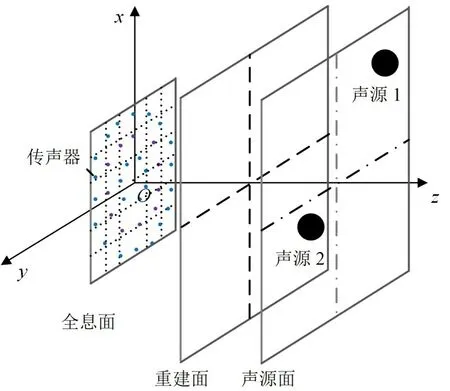
圖2 聲場空間位置示意

由式（2）可知，全息面上M個傳聲器測量的聲壓信息為P(t)，是時域信號，經過傅里葉變換為頻域信號，再進行下一步計算。假設等效源面上布置N個等效源，則全息面上的聲壓可表示為

式中，P?=[p(r1)p(r2)…p(rM)]T，Q為各等效源源強組成的列向量。G為等效源到全息面的傳遞矩陣，其中元素：

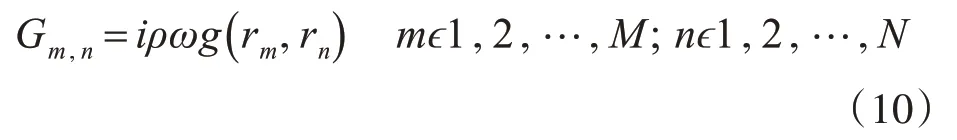
其中，g(rm，rn)為全息面上第m個傳聲器到第n個等效源的格林函數。

由式（9）可反解出源強：

式中，G+為G的廣義逆矩陣。為了保證解的唯一性，等效源的總數N應小于等于全息面上的測量點數M。采用Tikhonov正則化方法求解等效源強度，正則化參數由Hald經驗公式［17］確定。

由此，可計算出重建面聲壓：

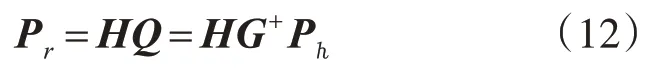
式中，H為等效源面到重建面的傳遞矩陣。

3 數值仿真

3.1 仿真設置

數值仿真參數設置如下：選取兩個振動頻率為1400Hz的非相干脈動球聲源，聲源半徑為0.005m，表面脈動速度為0.02m/s。根據3D-MUSIC算法定位特點，聲源可設在距傳聲器陣列中心0.01m～1m、俯仰角1°～90°、方位角1°～360°的任意位置，設置兩個聲源在笛卡爾坐標系下的位置分別為s1=（-0.4m，0.2m，0.6m）、s2=（0.2m，-0.1m，0.6m）。由傳聲器組成的全息面位于坐標原點所在平面，傳聲器陣列如圖1中的全息面所示，采用36個傳聲器組成三個同心圓的面陣列，三個同心圓半徑分別為0.07m、0.18m、0.25m。重建面位置在0.59m處，面積為1×1m2，網格點間隔為0.1m。

仿真過程中，重建誤差的計算公式如下：

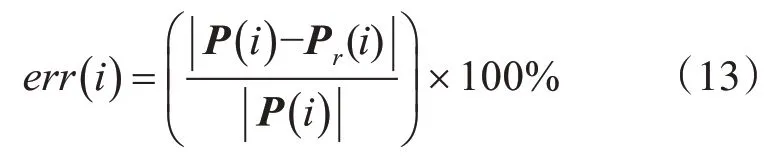
式中，P(i)為聲壓理論值；Pr(i)為聲壓重建值。

3.2 聲源定位

由3D-MUSIC算法定位聲源位置，其俯仰角、方位角和距離隨信噪比變化的均方根誤差曲線如圖3所示。隨著信噪比的增加，均方根誤差越來越小，這是因為3D-MUSIC算法中噪聲子空間和信號子空間的分離更加徹底。根據圖3的定位誤差分析，選擇在信噪比為20dB的條件下進行仿真。表1為在笛卡爾坐標系下，聲源理論坐標與算法定位結果的數值對比，兩個聲源的x軸定位誤差絕對值分別為0.009m和0.002m，y軸定位誤差絕對值均為0.001m，z軸定位誤差絕對值分別為0.017m和0.011m。由表1可以看出，在xoy平面上誤差在1cm以內，z方向上誤差在1cm～2cm之間，滿足定位精度要求。

圖3 均方根誤差曲線

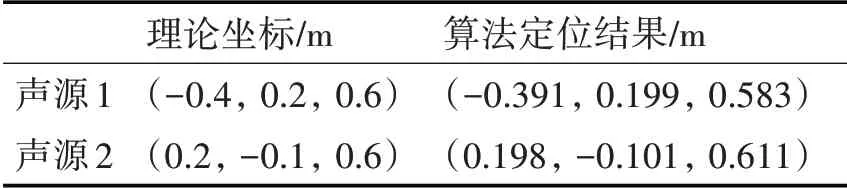
表1 理論位置與定位結果對比

3.3 聲場重建

由3D-MUSIC算法定位結果可知，聲源估計位置分別為（-0.391m，0.199m，0.583m）和（0.198m，-0.101m，0.611m）。根據該定位信息配置等效源，文獻［18～19］指出：等效源配置最好能與振動體表面共形，且等效源球面半徑與脈動球半徑之比在0.8以下，有較好的重建效果，另一方面，當等效源數目增加時，重建誤差會隨之減小。由此制定等效源配置策略：等效源面是一個以定位聲源位置為中心、0.01m為半徑的球面，在兩個聲源的等效源球面上分別布置16個等效源點。

圖4、5給出了兩種方法的重建效果。圖4是在z軸為0.61m的平面，等效源面大小為0.5×0.5m2，均勻布置6×6個等效源點的情況下，傳統波疊加法的重建值與理論值的對比結果，可以看出傳統波疊加法重建聲場的精度不高，這是因為等效源均勻分布在平面上時，等效源強度被均分，聲源位置處沒有重點布置等效源，重建值的峰值小于理論值。圖5是本文所提方法的重建值與理論值的對比結果，其重建值與理論值幾乎重合，重建精度較高。由此說明：利用3D-MUSIC算法對聲源位置進行估計，在聲源估計位置處密集布置等效源，聲場的重建值更接近理論值。圖6是兩種方法的重建誤差值隨頻率的變化趨勢，傳統波疊加法在1300Hz～3000Hz范圍內的相對誤差均大于15%，而本文所提方法的誤差在10%以下，重建誤差對比明顯。由此可以看出，本文所提方法可有效降低重建誤差，對聲場進行準確重建。

圖4 傳統波疊加法重建結果

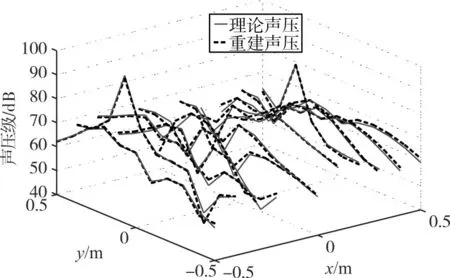
圖5 本文所提方法重建結果

圖6 重建誤差對比

4 實驗驗證

為進一步檢驗算法的可行性與準確性，在半消聲室進行實驗驗證。實驗設置如圖7所示。半消聲室尺寸為9.8m×8.6m×3.5m，背景噪聲為18dB（A），截止頻率為125Hz。采用兩個音箱模擬噪聲源，音箱位置分別為s1=（-0.4m，0.2m，0.6m）、s2=（0.2m，-0.1m，0.6m）。以傳聲器陣列的中心位置為坐標系原點，確定水平坐標x軸、豎直坐標y軸和測量坐標z軸，傳聲器陣列離地面高度為1.2m。傳聲器陣列為三個同心圓組成的面陣列，其參數與仿真設置一致。兩個音箱發出的聲信號是頻率為1400Hz的非相干聲源，利用傳聲器陣列和數據采集系統采集數據，再利用本文所提方法進行實驗驗證。

圖7 實驗布置

笛卡爾坐標系下，聲源理論坐標與3D-MUSIC算法定位結果的數值對比如表2所示。由表2可得，實驗中兩個音箱的算法定位誤差絕對值在x軸分別為0.019m和0.028m，在y軸分別為0.020m和0.012m，在z軸 分 別 為0.017m和0.004m。利 用3D-MUSIC算法進行聲源定位的實驗誤差在可接受范圍內，能夠較為準確地定位出聲源的空間三維坐標。以聲源定位坐標（-0.381m，0.220m，0.583m）和（0.172m，-0.112m，0.596m）為中心，以0.01m為半徑的球面上，分別配置16個等效源，利用波疊加法進行聲場重建，重建面在z=0.59m處，重建面大小為1×1m2，網格點間距為0.1m。

表2 理論位置與定位結果對比

聲場重建結果如圖8、9所示，圖8為傳統波疊加法重建值與理論值對比，圖9為本文所提方法重建值與理論值對比。實驗結果表明，傳統波疊加法的聲場重建值與理論值相差較大，這是因為平面上均勻配置等效源時，沒有對聲源位置處有針對性的布置等效源，使得重建峰值與理論峰值相差較大；而本文所提方法可以較為準確地重建聲場，說明在聲源估計位置處密集布置等效源，可提高聲場重建精度。圖10為兩種方法的重建誤差對比，可以看出，在1300Hz～3000Hz頻率范圍內，本文所提方法的重建誤差明顯低于傳統波疊加法的重建誤差，能夠更好地重建聲場，保證重建精度，驗證了本文所提方法的可行性與準確性。

圖9 本文所提方法重建結果

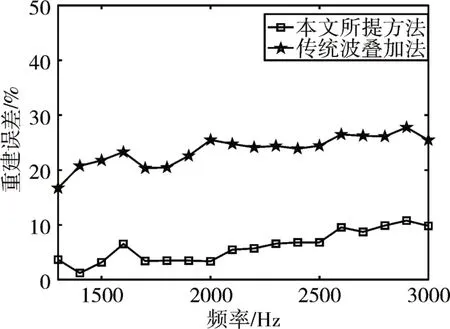
圖10 重建誤差對比

5 結語

為解決等效源配置不確定性問題，提出了基于3D-MUSIC和波疊加的聲場重建方法。數值仿真和實驗研究結果表明，該方法在1300Hz～3000Hz頻率范圍內，可有效定位聲源三維位置，準確重建聲場且重建誤差不高于10%。結論如下：

1）與傳統波疊加法的均勻分布方式相比，基于3D-MUSIC和波疊加的聲場重建方法的等效源布置是非均勻的，重點聲源布置更多的等效源點，能夠更好地模擬輻射聲場。

2）該方法精準配置等效源，降低了不必要的等效源數目，降低了求解方程的難度，提升了求解效率。

3）與現有的復雜三維定位方法相比，該方法利用3D-MUSIC算法直接定位聲源的空間位置信息，在保證準確重建聲場的基礎上，降低了計算復雜度，易于實現。

此外，本文實驗所用為兩個音箱模擬輻射聲場，后續可用板聲源或其他型聲源進行深入研究；本文采用36個測點進行聲場數據采集，在保證定位結果及重建精度的情況下，可進一步研究如何減少采樣點數，如引入壓縮感知理論等。