基于LSTM-BPNN-SVR的地鐵車輛軸箱溫度預測方法*

張瑋東

（上海地鐵維護保障有限公司車輛分公司 上海 200031）

1 引言

為了實現軌道交通智慧化運維［1］，上海地鐵車輛率先安裝了自發電式軌道車輛軸箱溫度在線感知及安全預警系統，該系統通過對列車運行過程中振動能量的捕獲，實現軌道車輛軸箱溫度自感知及數據預測。由于列車在運行過程中外部輪軌激勵呈現隨機性，使得該系統存在對軸箱溫度采樣頻率非線性問題，嚴重影響了軸箱溫度的預測精度及系統的可靠性。

目前針對樣本數據非等距預測研究中，主要通過對樣本數據的等距化處理，達到對目標數據的預測。如文獻［2］通過利用三次插值方法實現采樣數據的等距化處理實現了數據的預測；文獻［3］利用自然三次樣條插值法對滑坡位移數據進行等時距處理，達到了有效預測的效果；文獻［4］通過采用Lagrange插值函數將不等時距沉降序列轉換為等時距序列并建立預測模型，實現了對路基沉降的預測。然而，現有方法的樣本數據之間往往缺少關聯性分析，存在描述對象狀態變化特征有限的問題。為了增加數據集內部特征信息，文獻［5］通過將彼此關聯的多個監測點納入整體建模，使預測更為準確。文獻［6］通過合理地選擇多源空間相關數據，進行滑坡信息提取和分析并建立預測模型，達到了對滑坡災害信息的預測。文獻［7］針對掘進機振動信號、電流信號和油缸壓力信號非平穩、噪聲大的特點，對數據集特征提取和融合，有效提高了預測精度。然而，列車運行時各軸承溫度表現為強互相關性，且受牽引力等多個因素的影響，具有明顯動態性，造成傳統方法難以對其數據間的動態關系進行提取［8］。在預測模型方面，文獻［9］使用隨機森林構建了交通擁堵預測模型，實現了交通擁堵狀態的預測；文獻［10］通過建立多層LSTM預測模型實現了對軸溫的預測；文獻［11］使用BP神經網絡實現了對軸溫的預測；文獻［12］使用SVR預測模型實現了對地鐵咽喉區小凈距隧道圍巖位移的預測。但這些模型并未考慮到輸入特征與輸出特征關聯性，預測精度不高。且樣本數據本身不具有穩定和線性特性，使得單一模型預測方法往往效果不佳。組合預測模型因盡可能多地利用了各種預測子模型的全部信息，而逐漸被人們所接受［13］。為了實現對自發電式軌道車輛軸溫監測系統中的非線性采樣頻率所獲取的軸箱溫度數據的高精度預測，本文構建了一種基于LSTM-BPNN-SVR的地鐵車輛軸箱溫度預測方法。

2 數據等距化處理

利用K均值聚類［14］的方法分別對各監測傳感采樣數據集的差分結果(Δti，Δxi)進行可視化分析，以獲得簇中心所在位置(tI，u，xI，u)的采樣數據特征tI，u，作為分段三次Hermite插值［15］樣本點間隔長度Δξ的設定依據［5］。K均值聚類算法模型如式（1）～（3）所示，分段三次Hermite插值法如式（4）所示。

式中，E表示最小化平方誤差；k表示類（簇）的個數；m為簇中對象的總個數；( ΔtI，j，ΔxI，j)表示第I簇的第j個數據對象；(tI，u，xI，u)是類CI的均值向量，也稱為第I簇的均值中心；Δti表示數據集第i個樣本點時刻ti與第i-1個樣本點時刻ti-1的差值；Δxi表示數據集第i個樣本點數據xi與第i-1個樣本點時刻xi-1的差值。CI表示對差分結果劃分為的類，其中I=1，2，…，k。xi和x′i是樣本點ti處的函數值和一階導數值；插值節點tδ=t1+n·Δξ；四個插值基函數φi(tδ)，φi+1(tδ)，φi(tδ)，φi+1(tδ)如式（5）～（8）：

3 LSTM-BPNN-SVR預測模型構建

LSMT-BPNN-SVR預測模型構建流程如下。

第一步：對等距樣本Zq進行數據分組得到樣本矩陣Wq，如式（9）所示。使用Wq對組合模型進行訓練，其中訓練集的樣本數量為g個；

第二步：將樣本矩陣Wq中每組數據（行）依次輸入LSTM模型，構建出雙重時間序列。其中LSTM模型的輸入和輸出如式（10）、（11）所示，雙重時間序列，如式（12）所示；

第三步：將構造出的雙重時間序列，作為BP神經網絡的輸入，完成對Zq中第i+1個樣本數據zi+1的預測，BP神經網絡的輸入和輸出如式（13）、（14）所示；

第四步：BP神經網絡的輸出結果，通過SVR模型對BP神經網絡輸出結果與Zq數據集中對應樣本點數據構建的回歸模型，得到混合模型的最終預測結果。其中，SVR模型的輸入和輸出為和如式（15）所示，最終預測結果如式（16）所示。在預測結果中，表示為LSTM-BPNNSVR預測模型對Zq中第i個樣本數據的預測結果。最后，對基于多源融合有效數據集Zq構建的組合模型記為LSTM-BPNN-SVR預測模型。

上式中，為由LSTM模型對Zq中第i+1個樣本數據zi+1的預測值，表示BP神經網絡對Zq中第i+1個樣本數據zi+1的預測值。

4 實驗驗證

為了驗證基于LSTM-BPNN-SVR的地鐵車輛軸箱溫度預測方法的有效性，實驗數據均來自上海地鐵的軌道車輛軸箱溫度監測及預警系統，該系統結構圖由如圖1所示，該系統由安裝于轉向架上的溫度監測傳感器以及設置在車廂內的數據中繼器模塊和車載主機構成。在列車運行過程中將列車振動能量轉換為電能為傳感器供電，由于外界振動激勵的隨機性，導致樣本數據存在非等距化的問題。選取地鐵車輛軸承故障易發的6月至7月間同一節車廂下8個軸箱溫度的監測數據［16］，并以1傳感器采集到的數據為目標數據集。為了量化預測效果，將LSTM-BPNN-SVR預測方法與常規的6種預測方法進行對比，采用平均絕對百分比誤差（MAPE）、平均絕對誤差（MAE）、均方根誤差（RMSE）和擬合度（R-squared）［17］四個評價指標如式（17）～（20）：

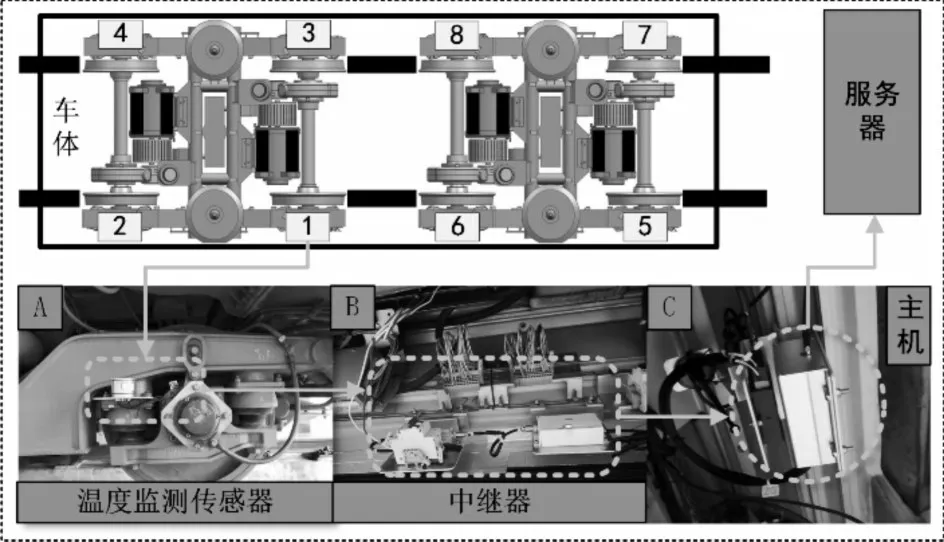
圖1 自發電式軸溫監測系統結構圖

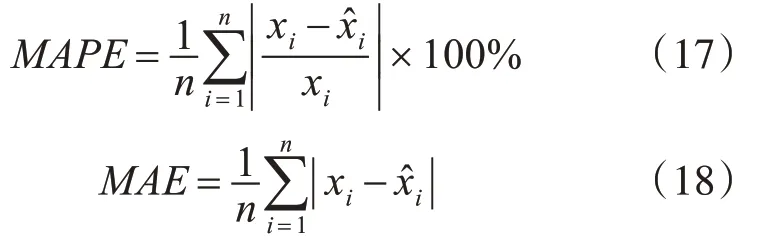
式中，xi為樣本數據，為預測數據，為xi的均值，n為樣本數量。其中R-squared越接近1，表示回歸擬合度越好，MAPE、MAE、RMSE這三項數值越小說明算法的精確度越高。

LSTM-BPNN-SVR預測結果如圖2所示，從圖2可以看出，LSTM-BPNN-SVR預測值與實測值數據一致偏差較小；由圖2進一步可以看出LSTM-BPNN-SVR預測輸出曲線與實測溫度數值曲線都呈鋸齒狀的線型且擬合度較高，說明預測結果可以較精確反映出軸箱溫度變化情況，達到對軸箱溫度的有效預測。

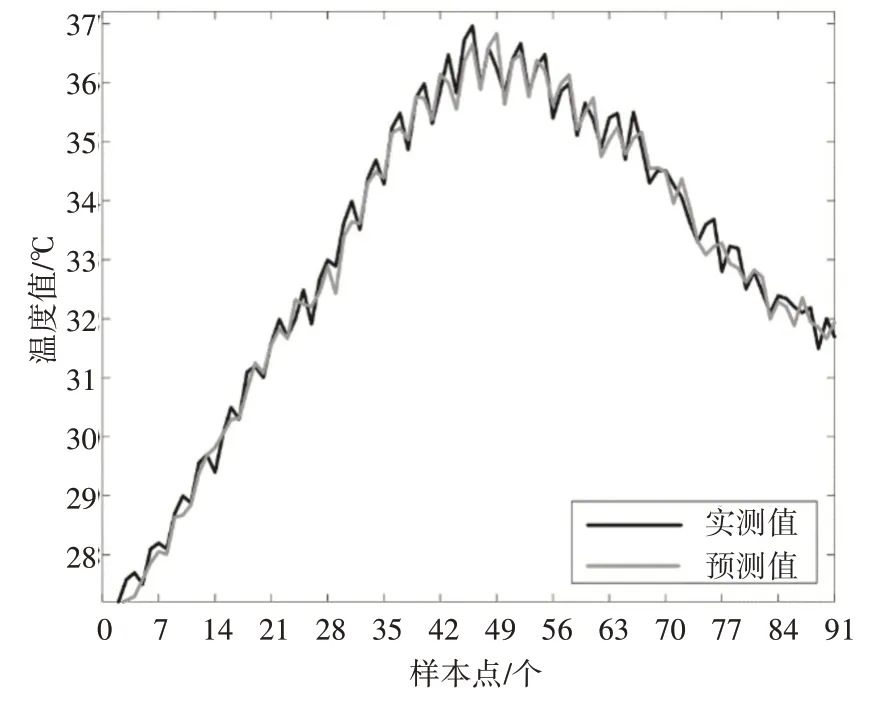
圖2 LSM-BPNN-SVR預測模型預測結果曲線對比圖

表1為各預測方法的評價指標，從表1可以看出，LSTM預測模型R2為0.95，與其他算法相比預測精度偏低。而LSTM-BPNN-SVR預測模型在MAPE/MAE/RMSE/R2四項評價指標均優于LSTM、BP神經網絡和SVR預測模型，并且與其他隨機森林、Arima、RNN相比各項評價指標均有提升，其中擬合度R2達到0.9915，說明LSTM-BPNN-SVR組合預測模型有效融合了多個預測模型的優勢，具有較好的預測效果。

表1 各種預測方法的評價指標

5 結語

通過利用K均值聚類和分段三次Hermite插值法對上海地鐵車輛自發電式軌道車輛軸箱溫度在線監測及安全預警系統的樣本數據進行等距化處理，基于此數據集構建了LSTM-BPNN-SVR組合預測模型，實現了軌道車輛軸箱溫度零碳感知及溫度預測，結果表明預測精度可達到99.15%。