Fe 原子吸附的銻烯/WS2 異質結的磁電子性質及調控效應*

何鑫 李鑫焱 李景輝 張振華

(長沙理工大學,柔性電子材料基因工程湖南省重點實驗室,長沙 410114)

為研究非磁性二維范德瓦耳斯異質結吸附磁性原子的誘發磁性機理及磁電子特性,構鍵了銻烯(Sb)/WS2異質結,并考慮Fe 原子的多種吸附.計算的吸附能表明: TW,TS_m 及VSb 吸附方式是Fe 原子分別吸附于異質結下方、層間以及上方的最可能吸附位置,產生的磁性與Fe 原子被吸附后其電子構型(VEC)擴展以及電荷轉移使得電子自旋重排有關.TW,TS_m 吸附使無磁半導體性的異質結成為半-半導體(HSC),而VSb 吸附對應雙極化磁性半導體(BMS).特別是,計算的磁化能表明: 層間TS_m 吸附使異質結具有最高的磁穩定性,足以抵抗常溫熱起伏對磁性的影響.量子調控能使異質結產生豐富的磁性,特別是磁相的靈活改變,如施加外加電場可使異質結實現HSC,HM(半金屬)及BMS 等磁相轉換,而垂直應變則可使異質結發生HSC,HM 及MM(磁金屬)等磁相的轉換.這一研究表明利用異質結能增加過渡金屬原子的吸附區域(下方、層間以及上方),從而產生豐富的磁性,特別是層間吸附過渡金屬,其磁性的溫度穩定性能顯著提高.

1 引言

范德瓦耳斯異質結[1-5],即通過范德瓦耳斯相互作用將兩種或多種不同的二維層狀材料堆疊在一起而得到的新的層狀材料,因具有兩種單層材料單獨存在時不具備的優異物理性質,而引起研究者的廣泛研究興趣.按照兩單層能帶對齊方式不同,異質結可分為三類[6]: Ⅰ-型,Ⅱ-型及Ⅲ-型.其中Ⅰ-型異質結的導帶底(CBM)和價帶頂(VBM)均來自于同種單層材料,因此能使電子和空穴高效復合,該類異質結可廣泛應用于光電納米器件,例如:WSe2,石墨烯與hBN 三者構成的Ⅰ-型異質結能通過納米腔使其電致發光強度提高4 倍,電致發光速度可達1 MHz,這對于制備發光二極管具有明顯地潛在優勢[7,8].Ⅱ-型異質結的CBM 與VBM分別由兩種不同單層材料所貢獻,由于能帶偏移,導致兩材料的CBM 與VBM 分別錯開,這有利于在場效應晶體管、光催化和能量轉化、壓電效應等方面的應用,如銻烯/WS2異質結[9]具有較高的開關比和BP/MoS2p-n 異質結[10]具有較強的整流效應,使得他們在邏輯電路中具有重要應用.HTiO2/MoS2(WS2)異質結[11]具有較高的光吸收強度,可用于光催化分解水和太陽能轉換器件[12].Ⅲ-型異質結由于一種材料的CBM 與VBM 與另一種材料的CBM 與VBM 完全錯開,故在隧穿場效應晶體管和光波探測儀方面具有重要的應用前景,例如: WTe2/HfS2[13],BP/ SnSe2[14]及BP/ReS2[15]異質結,外加正向電場作用能使其隧穿窗口變大,有望研發高性能隧穿二極管.負電場可以實現磷烯/SnS2(SnSe2)異質結[16]能帶對齊方式之間的轉化,有利于實現多功能納米電子及光電子器件.

然而,目前研究的異質結大都為無磁結構,限制它們在自旋電子器件方面的應用,因此,在異質結的基礎上如何誘導磁性,最近也有一些研究,例如: 過渡金屬原子(V,Cr,Mn,Fe,Co,Ni)吸附于MoS2/h-BN 異質結,能誘導磁金屬(Cr)、半-半導體(V,Mn,Fe)及半金屬(Co)性質[17].而Sc,Ti,V,Cr,Mn 吸附于Blue P/MoS2異質結導致無磁半導體轉變成磁金屬[18].研究表明,缺陷也能誘發磁性,如: 缺陷能使雙層磷烯出現磁性[19].過渡金屬摻雜也構成誘發異質結磁性的重要方法,如: Mn摻雜MoS2/SiC 異質結能導致層間出現反鐵磁(AFM)耦合,計算的磁各向異性能表明其磁性與a軸方向平行,在拉應變下始終保持AFM 耦合,而在外加壓力下能使AFM 耦合變為鐵磁(FM)耦合[20].雖然Sc,Ti,V,Cr 和Mn 摻雜InSe/磷烯異質結導致體系是AFM 基態,但是Fe 摻雜為FM耦合,Co 摻雜為弱的順磁耦合[21].總之,對二維異質結誘發磁性已構成二維材料研究的重要課題.

構鍵Sb/WS2異質結,細節研究了Fe 原子吸附于Sb/WS2異質結誘發磁性的機理及磁電子特性.計算表明: 如此吸附能產生半-半導體(HSC)及雙極化磁性半導體(BMS).特別是,層間TS_m吸附使異質結具有最高的磁穩定性,足以抵抗常溫熱起伏的影響.量子調控能使異質結產生豐富的磁性,特別是磁相的靈活改變,如施加外加電場可使異質結實現HSC,HM(半金屬)及BMS 等磁相轉換,垂直應變則可使異質結發生HSC,HM 及MM(磁金屬)等磁相的轉換.這些發現對于異質結誘發磁性的研究基礎及實際應用都有一定的意義.

2 計算方法

模型的幾何優化、結構穩定性的評估和磁電子學特性的計算采用基于密度泛函理論(DFT)的第一性原理方法.所有這些計算都是在Atomistix ToolKit(ATK)軟件包中實現,該軟件已被廣泛應用于低維材料電子及磁電子性質的研究[9,22-30].為了求解Kohn-Sham 方程,交換關聯勢采用廣義梯度近似(GGA)中的Perdew-Burke-Ernzerhof(PBE)近似計算無磁結構,而對有磁結構,交換關聯勢采用自旋依賴性的廣義梯度近似(SGGA).用Troullier-Martin 模守恒贗勢代表原子核,并用原子軌道的線性組合展開價電子波函數,基函數組選為DZP(Double ζ+Polarization),截斷能設置為400 eV.對于模型優化和磁電子性質的計算,其布里淵區的k點采樣分別采用7×7×1 和9×9×1.在垂直二維平面的z軸方向上設置一個大于20 ?的真空層以消除模型與“像”之間的相互作用.并采用Grimme DFT-D2 函數來修正層間的范德瓦耳斯相互作用[31].其幾何優化的收斂標準為作用在每個原子上的殘余應力小于10-2eV/?,能量收斂標準為10-5eV.另外,之前的研究發現在不考慮自旋-軌道耦合(SOC)作用的情況下也能對Sb/WS2[9]異質結的電子光學性質進行很好的描述,因此在本文中為了節約計算成本,不考慮SOC 作用.所有的計算都在幾何結構優化之后進行,為了簡單起見,系統的費米能級設置為零.

3 計算結果與分析

3.1 Sb/WS2 異質結的幾何結構與電子性質

首先,分別構建并優化兩個單層的單胞,在此基礎上組合成Sb/WS2異質結,為了減少兩個單層之間的失配率,采取3×3×1 的銻烯矩形胞(a=12.319 ?,b=21.336 ?,包含36 個原子)和4×4×1的WS2矩形超胞(a=12.613 ?,b=21.846 ?,包含96 個原子)來構建Sb/WS2異質結單胞,計算得到在a和b方向的晶格適配率分別低至2.361%與2.362%.考慮了4 種堆垛方式,如圖1(a)-(d)所示,A1: 考慮最右上邊的Sb 原子與W 原子對齊;A2: 考慮最右上邊的Sb 原子位于W-S 原子之間向左下1/4 處;A3: 考慮最右上邊的Sb 原子位于W-S原子之間向左下1/2 處;A4考慮:考慮最右上邊的Sb 原子與S 原子對齊.總之,把WS2當作是固定不動的襯底,可以通過沿水平方向滑動Sb 層實現各種堆垛模型之間的相互轉換.構成異質結并優化之后,4 種堆垛模型都很好地保留了各自單層時結構的完整性,無任何顯著形變發生.理論上可以通過計算結合能[32]、內聚能[33]等來評估異質結的能量穩定性,這里我們利用面結合能加以說明,其定義為[32,34]

其中,ESb/WS2,ESb,EWS2分別代表異質結、Sb單層以及WS2單層的總能量,A表示異質結的面積,計算結果如圖1(e)所示.顯然,它們介于-16.7 meV/?2至-17 meV/?2之間.由于優化前后銻烯和WS2的晶格基本沒有變化,則(1)式可以表示異質結形成的難易程度,即負值越大,異質結越容易實現[35].而負的Eb,對應一個能量穩定的結構,所以這4 種異質結在能量上都是穩定的.其中,A2是結合能是最低的情況,對應最穩定的堆垛方式,是實驗上最可能實現的異質結.所以,下文中我們只對A2堆垛方式的異質結進行研究.在圖1(e)中,也可看出不同堆垛的層間距d有一定的差別,對于這4 種異質結,層間距分布在3.413-3.512 ?范圍內.

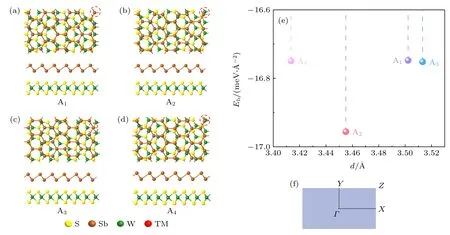
圖1 (a)-(d)優化之后Sb/WS2 異質結的四種堆垛方式的主視圖和側視圖;(e)優化后不同異質結的層間距與結合能;(f)異質結單胞對應的布里淵區Fig.1.(a)-(d)Top and side views of the four stacking patterns of optimized Sb/WS2 heterostructures;(e)the binding energy and interlayer distance of the optimized heterostructures;(f)Brillouin zone corresponding to heterostructure unit-cell.

圖2 所示為異質結相關單層及Sb/WS2異質結(A2)的電子結構.PBE 計算(見圖2(a)-(c))表明: Sb 單層為間接帶隙半導體,其帶隙為1.219 eV,CBM 位于Γ點,VBM 位于Z點,雖然在數值上多體微擾GW方法比GGA 方法得到的帶隙值更準確一些,但計算成本也比GGA 方法高出很多,并且GGA 方法得到的能帶結構總體上與GW方法得到的是一致的,且結果都為間接帶隙半導體,因此,采用GGA 方法來對銻烯的電子性質進行研究也是可行的[9,36,37].而WS2單層則為直接帶隙半導體,其帶隙值為1.949 eV,CBM 和VBM 都位于Γ-X之間.形成異質結之后,雖然得到的是一個與Sb 單層一樣的間接帶隙半導體,但是其CBM 位于X-Z,VBM 位于Z點,且帶隙相對于兩單層減少,變為1.043 eV.這是由于銻烯與WS2構成的異質結為Ⅱ-型能帶對齊,即兩個單層的CBM 與VBM 互相錯式,且異質結的CBM 來自WS2,而VBM 來自銻烯,因此帶隙變小.這些結果與之前的研究結果相一致[9,11,37].小帶隙半導體有利于電子從價帶躍遷導帶,從而提高對光的吸收.另外,之前的研究已經證明PBE 計算會低估帶隙值[9,31],所以作為比較,利用HSE06 也計算了Sb 單層、WS2單層以及Sb/WS2異質結的能帶結構(見圖2(d)-(f)),發現PBE 計算相對HSE06計算,的確低估帶隙的大小,但整個帶結構非常相似,特別是費米能級附近的能帶結構與帶隙類型(直接或間接)幾乎完全一樣.眾所周知,HSE06計算的機時成本較大.所以為了在計算精度與計算效率之間取得平衡,在接下來的研究中,僅采用PBE 計算預測異質結的電子及磁性質.

圖2 PBE 計算的(a)Sb 單層、(b)WS2 單層和(c)Sb/WS2 異質結的能帶結構;HSE06 計算的(d)Sb 單層、(e)WS2 單層和(f)Sb/WS2 異質結的能帶結構Fig.2.Band structures by PBE calculation:(a)Sb monolayer;(b)WS2 monolayer;(c)Sb/WS2 heterostructure.The band structures by HSE06 calculation:(d)Sb monolayer;(e)WS2 monolayer;(f)Sb/WS2 heterostructure.

3.2 Fe 原子吸附的Sb/WS2 異質結的幾何結構與磁電子性質

如圖3 所示,考慮在異質結上吸附Fe 原子來誘發磁性,且一個異質結單胞吸附一個Fe 原子.為了系統研究吸附情況,將吸附模型大致分為三類,第一類如圖3(a)所示,Fe 原子僅吸附于WS2單層,其中TW: Fe 原子吸附于W 原子正下方;TS:Fe 原子吸附于S 原子正下方,: Fe 原子吸附于WS2中W-S 的六連環正下方;: Fe 原子吸附于W-S 鍵中點正下方.第二類如圖3(b)所示,Fe 原子吸附于異質結的層間,其中: Fe 原子吸附于WS2中W-S 的六連環正上方,TS_m:Fe 原子吸附于S 原子正上方,VSb_m: Fe 原子吸附于Sb 層底層Sb 原子的正下方,HSb_m: Fe 原子吸附于Sb 六連環的正下方.第三類如圖3(c)所示,Fe 原子僅吸附于Sb 單層上方,其中VSb: Fe 原子吸附于Sb 層的底層Sb 原子的正上方;TSb: Fe 原子吸附于Sb 層的頂層Sb 原子的正上方;HSb:Fe 原子吸附于Sb 層中Sb-Sb 的六連環正上方;BSb: Fe 原子吸附于Sb-Sb 鍵中點的正上方.

圖3 過渡金屬原子Fe 吸附于Sb/WS2 異質結的四個高對稱位置(a)底層WS2 下方;(b)兩單層層間;(c)上層Sb 上方Fig.3.Four highly symmetrical adsorbed sites of Fe atom for Sb/WS2 heterostructure:(a)Bellow the bottom WS2 monolayer;(b)between two monolayers;(c)above the top Sb monolayer.

對于三類吸附模型的不同吸附位置分別計算吸附能,其定義為

其中Etotal,,EFe分別代表吸附之后系統的總能量,吸附之前Sb/WS2異質結的總能量,自由狀態下Fe 原子的能量,根據定義可知,負的Ea對應一個放熱反應,正的Ea對應一個吸熱反應,計算結果發現所有的吸附模型都為放熱反應,即Fe 原子吸附有利于提高結構的穩定性.三類吸附中,吸附能最低的模型是TW,TS_m及VSb,其吸附能分別為-7.087 eV(TW),-7.754 eV(TS_m),及-7.668 eV(VSb),分別對應三類吸附中的最穩結構.所以下面僅對這三種最穩吸附結構的磁電子特性進行研究.

利用自旋極化的交換關聯函數分別計算三種最穩吸附體系的鐵磁態(FM)和反鐵磁態(AFM)能量,以發現體系的磁耦合特性及磁基態.首先將單個的Fe 吸附異質結之后的體系擴胞兩倍,再將該超胞中所有Fe 原子的自旋方向設置為同一方向,這即為FM 態,而將體系中兩兩相鄰Fe 原子的自旋方向設為相反方向,這即為AFM 態.通過計算發現,FM 態與AFM 態的能量基本一致,這是由于我們采用的是一個極低的吸附濃度(0.76%),即兩個相鄰Fe 原子之間的吸附距離較遠,導致他們之間的磁耦合很弱,其反鐵磁耦合可以忽略不計[32].換言之,在如此理論模型下,我們的研究可以看作是異質結與磁矩指向同一方向的完全分離的磁性Fe 原子的作用.

為了發現磁性分布,計算了體系在FM 態下的自旋極化密度,其定義如下:?ρ=ρα-ρβ,其中ρα和ρβ分別代表α-自旋(品紅色)和β-自旋(黑色)的電荷密度,計算結果如圖4 所示.不難看出,對于異質結下方的TW吸附(圖4(a)),磁性主要分布在Fe 原子,與之共價結合的W 原子與S 原子也有少量貢獻,而Sb 原子基本無磁性.對于異質結層間的TS_m吸附(圖4(b)),磁性也主要分布在Fe 原子上,與之共價結合的Sb 和S 原子、以及與該S 原子共價結合的兩個W 原子也有少量磁性分布.而對于異質結上方的VSb吸附(圖4(c)),與前2 種情況基本類似,即磁性主要分布在Fe 原子上.與之共價結合的3 個Sb 原子也有少量磁性,WS2基本沒有磁性.總的來說,吸附之后系統的磁性主要是由Fe 原子所貢獻,與之共價結合的原子也會誘發少量磁性,這說明磁性原子在二維異質結中誘發的磁性具有高度局域化特性.

圖4 FM 態自旋極化密度分布,對應的吸附方式分別為(a)TW,(b)TS_m,(c)VSb.等值面取為0.002 e/A3Fig.4.Spin-polarized density(magnetic distribution)in the FM state,and corresponding adsorbed manners are:(a)TW;(b)TS_m;(c)VSb.The isosurface is set as 0.002 e/A3.

為了探究磁性根源及磁機理,計算吸附的Fe 原子和體系的總磁矩,其結果如表1 所列.顯然,對于TW,TS_m及VSb三種吸附方式,Fe 原子磁矩分別為2.002 μB,2.002 μB及2.004 μB,體系的總磁矩分別為2.313 μB,2.290 μB,2.023 μB,這說明Fe 原子是系統磁矩的主要貢獻者,與上文看到的磁分布(圖4)完全一致.然而,相對孤立狀態的Fe 原子磁矩(4 μB),Fe 原子被吸附之后其磁矩都減少了2 μB左右.如何理解這種現象? 這是由于Fe 原子被吸附后其電子構型(VEC)擴展以及電荷轉移發生使得電子自旋重排所致[32-34].Fe 原子電子構型(VEC)發生擴展是因為Fe 原子受到異質結作用所致,包括Fe 原子與異質結的軌道雜化及耦合效應.計算的吸附前后Fe 原子的VEC以及利用Bader 電荷分析計算的電荷轉移ΔQ如表1 所列.孤立Fe 原子的電子態為3d64s2,而吸附之后,對于TW,TS_m及VSb三種吸附方式,3d 軌道都得到了電子,4s 軌道失去電子,孤立狀態本來無電子占據的4p 軌道吸附后卻出現了電子占據,這說明吸附后Fe 原子的4s 電子轉移到了3d 軌道及4p 軌道,還有部分電荷轉移至Sb/WS2異質結的其他原子上,分別為0.423|e|,0.119|e|,0.065|e|.為什么不同吸附方式(TW,TS_m及VSb)中電荷轉移不同呢? 這是由于Fe 原子與成鍵原子(Sb,W,S)的電負性存在差異所致.對于VSb吸附,由于Fe 原子僅與Sb 層發生直接相互作用,且Fe 原子的電負性(1.83)小于Sb 原子的電負性(2.05),所以導致電荷從Fe 原子轉移到Sb 層,而Fe 原子與底層的WS2層相距較遠,二者之間不發生電荷轉移.而對于TW吸附方式,與VSb相似,只是Fe 原子僅與WS2層發生直接相互作用,W 原子(2.36)與S 原子(2.58)的電負性都比Fe 原子的電負性大得多,因此,W 原子、S 原子都從Fe 原子得到電子,特別是,相對于Fe 原子與Sb 原子的電負性差值而言,Fe 原子與W,S 原子的電負性差值更大,導致TW吸附位置時的電荷轉移是最多.而對于TS_m吸附,Fe 原子位于兩單層層間,Fe 與S,W,Sb 原子之間存在電負性差異,這導致Fe 原子的電荷不僅會轉移到Sb 層上,也會轉移到WS2層.假定Fe 原子首先轉移電荷到Sb 層后,Fe 離子與S,W 原子間的電負性差值會相應減小,導致轉移到WS2層的電荷減少,即Fe 原子失去電子后,使得原子核對電子的束縛作用增強,導致Fe 離子失去電子(轉移到WS2層)難度增大,反之亦然,或者說Fe 原子轉移出去的電子取決于Sb,S 及W 原子的平均電負性.因此TS_m方式吸附時,Fe 原子失去的電子介于TW與VSb吸附方式之間.

表1 磁矩、TM 原子電子構型、電荷轉移和磁化能.μ0 為孤立Fe 原子的磁矩,μ為Fe 原子吸附后磁矩,括號中M 為超元胞磁矩.VEC 為孤立Fe 原子價電子構型(valence electron configuration),VEC*為Fe 原子吸附后價電子構型.ΔQ 為吸附之后Fe 原子所轉移的電荷,“-”代表 Fe 原子失去電荷.EM 為磁化能Table 1. Magnetic moment,electron configuration of TM atom,charge transfer and magnetization energy.μ0 is the magnetic moment of isolated Fe atoms,μ is the magnetic moment after adsorption of Fe atoms,M in parentheses is the magnetic moment of the supercell.VEC is the valence electron configuration of isolated Fe atoms,and VEC*is the valence electron configuration of Fe atoms after adsorption.ΔQ is the charge transferred by Fe atom after adsorption,where “-” means that the Fe atom loses its charge.EM is the magnetization energy.

為了比較不同吸附方式的磁穩定性,計算體系的磁化能,定義為

其中ENM和EFM分別表示Fe 吸附之后體系在無磁(NM)態和鐵磁(FM)態時的總能量,而n代表該體系中磁性原子數目,計算結果如表1 所列.顯然,對于三個吸附位置而言,FM 態均為體系的基態.EM越大意味著磁基態越穩定.顯然,TS_m具有最高的EM(146.46 meV/磁性原子),如此大的EM足以抵抗室溫下的熱起伏(T=300 K,kBT=26 meV),即在遠高于室溫條件下,磁性體系也具有磁穩定性,在這種情況,Fe 原子與上下單層成鍵,從而增加了異質結的磁穩定性是不難理解地.對于VSb吸附,磁化能只有10.02 meV/磁性原子,即在室溫條件下,體系不能保持磁穩定性,材料受熱起伏的影響發生磁基態轉變,變為無磁態.而TW吸附,系統磁化能為75.3 meV/磁性原子,這說明在室溫下系統的磁性仍是穩定地,但比TS_m吸附情況低很多.

圖5(a)-(c)所示為TW,TS_m,VSb三個吸附位置時異質結自旋極化的能帶結構.據此,能確定磁性異質結的吸附位置依賴性的不同磁相.顯然,TW與TS_m吸附方式使異質結從無磁半導體轉變為磁性半-半導體(HSC),即一種自旋的帶隙落在另一種自旋的帶隙內.對于本文情況,異質結α-自旋的CBM 與VBM 構成的帶隙落在β-自旋的CBM與VBM 構成的帶隙內,但TW吸附時α-自旋的CBM 與VBM 都出現在Γ點,帶隙值為0.454 eV,而TS_m吸附時α-自旋的CBM 與VBM 皆位于Z點,帶隙值為0.209 eV.然而,VSb吸附的情況是不同的,它誘導雙極化磁性半導體(BMS)性質,其β-自旋的CBM 位于Γ點,α-自旋的VBM 位于Y點,對應的自旋翻轉帶隙(spin-flip gap)為0.249 eV.眾所周知,不同磁相的材料對于制備不同功能的納米磁器件都有重要應用.

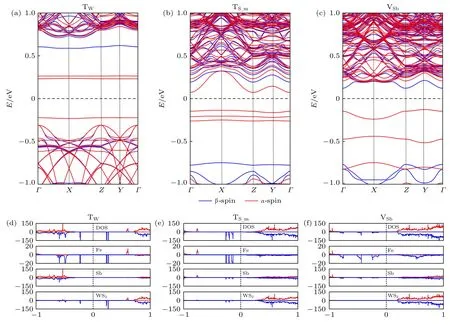
圖5 對應最穩三種吸附位置的異質結能帶結構、態密度以及投影態密度(a)-(c)能帶結構;(d)-(f)態密度和投影態密度Fig.5.Band structure,density of states and projected density of states of the heterostructures corresponding to three most stable adsorption sites:(a)-(c)Band structure;(d)-(f)density of states and projected density of states.

為更細節討論磁性分布及來源,計算系統的總態密度(DOS)以及投影態密度(PDOS),如圖5(d)-(f)所示,其中PDOS 為將DOS 分別投影到Fe 原子、Sb 單層及WS2單層的態密度.明顯地,它們的α-自旋與β-自旋態密度是非對稱的,對應自旋極化即磁性,特別是,Fe 原子的PDOS 具有高度非對稱性,所以磁性主要是來源于Fe 原子.同時,能看到Fe 吸附使Sb 單層和/或WS2單層的PDOS也出現非對稱性,即本征無磁的單層也誘發出磁性.但不同的吸附位置,DOS 及PDOS 也有明顯差異,例如,對于Tw吸附(圖5(d)),費米能級附近的α-自旋DOS 由Fe 原子及WS2層所貢獻,Sb層基本沒有貢獻,同時我們發現在費米能級附近Fe 原子與WS2層α-自旋的PDOS 峰能很好對齊,這意味著兩者有強的軌道耦合及自旋轉移.對于TS_m吸附(圖5(c)),費米能級附近α-自旋DOS由Fe 原子、Sb 層及WS2層共同所貢獻,這三者α-自旋的PDOS 峰的對齊意味著它們之間均有強的軌道耦合及自旋轉移.而對于VSb吸附(圖5(f)),靠近且在費米能級以下的α-自旋DOS 由Fe 原子及Sb 層所貢獻,靠近且在費米能級以上的β-自旋DOS 由WS2層所貢獻.從圖5(d)-(f)還可以看出,吸附Fe 原子后在本征異質結能帶(見圖2(c))帶隙內產生的子能帶(gap-state,見圖5(a)-(c)),來源于Fe 原子以及Fe 原子與單層的相互作用(軌道雜化與耦合).

3.3 量子調控效應

下面,簡單討論Fe 原子吸附的異質結磁性的量子調控效應,本工作僅考慮兩種情況: 施加垂直電場及垂直應變.眾所周知,外加垂直電場(Eext)是一種有效調節納米材料電子特性及磁性的重要手段,這里,以磁穩定最高的TS_m方式吸附的異質結為例,說明外加電場對體系磁電特性的調控效應.將相關體系置于相距10 ?的兩極板之間,Sb層靠近上極板(正極),而WS2層靠近下極板(負極),由此產生一個從Sb 層指向WS2層的外加正電場,如圖6(a)所示,若外電場反向則稱為負電場.為了檢驗外電場對結構穩定性的影響,計算體系的電場能,定義為: ΔE=EV-E0,其中EV(E0)代表施加(未施加)外電場時體系在FM 態的總能量,計算表明: 不管Eext為正或為負,ΔE總為負值,且為開口向下的拋物線,如圖6(b)所示,說明外加電場能使系統的穩定性提高.特別是,外加電場能有效地調節體系的帶隙,如圖6(b)所示.在正電場范圍內,帶隙首先減小(0 V/?＜Eext＜0.5 V/?),在Eext=0.5 V/?時,帶隙減小為0,且保持至0.6 V/?,之后帶隙上升直至Eext=0.9 V/?,再繼續增加電場強度,其帶隙急劇減小為0.而在負電場范圍內,帶隙首先增大,當Eext=-0.2 V/?時帶隙達到最大值,之后帶隙緩慢下降,直至Eext=-0.9 V/?時,帶隙又變為0.伴隨帶隙的非規則性變化,磁相也做相應變化,如圖6(b)所示,在-0.3 V/?＜Eext≤0.4 V/?時,體系保持原有的HSC 性質.在其他正電場范圍內,當滿足0.4 V/?＜Eext≤0.6 V/?時,體系變為半金屬(HM),若滿足0.6 V/?＜Eext≤0.9 V/?時,體系又變為HSC,在Eext≥0.9 V/?時,體系又變回HM.而在其他負電場范圍內,當滿足-0.5 V/?＜Eext≤-0.3 V/?時,體系變為BMS,當滿足-0.8 V/?≤Eext≤-0.5 V/?時,體系為HSC,在Eext＜-0.8 V/?時,體系變為HM.

圖6 (a)外加電場示意圖;(b)電場能、帶隙值及磁性隨加電場變化;(c)-(j)Eext=-0.1,-0.3,-0.7,-1,0.2,0.5,0.8 和1.0 V/?時的能帶結構,其中圖(d)中綠色區域代表該陰影部分的能帶放大圖Fig.6.(a)Schematic diagram of applied external electric field on heterostructure.(b)Electric field energy,band gap,and magnetic phase versus the external electric field.(c)-(j)The band structures for Eext=-0.1,-0.3,-0.7,-1,0.2,0.5,0.8,and 1.0 V/?,where the green region in panel(d)represents the enlarged partial band structure.

為了更清楚地呈現Eext對體系磁電子特性調控效應,特別是磁相過渡的細節,畫出Eext=-0.1,-0.3,-0.7,-1,0.2,0.5,0.8 和1.0 V/?時能帶結構,如圖6(c)-(j)所示.在負電場范圍內,Eext=-0.1 V/?,這個小的外電場僅導致能帶發生微小改變,所以帶隙略有增加,但體系仍為HSC;當Eext=-0.3 V/?時,體系的CBM 及VBM 來源于兩種不同的自旋,所以體系變為BMS;在Eext=-0.7 V/?時,體系能帶的CBM 與VBM 都來源于α-自旋,體系又變成HSC;當Eext=-1.0 V/?時,體系有α-自旋子能帶穿過費米能級,此時體系變為HM.而在正電場范圍內,當Eext=0.2 V/?,由于CBM 與VBM 向費米能級靠近,體系帶隙會變小,但體系能帶的CBM 與VBM 都來源于α-自旋,所以體系仍為HSC;在Eext=0.5 V/?時,體系有α-自旋子能帶穿過費米能級,使得體系轉變為HM;而之后,在Eext=0.8 V/?時,原穿過費米能級的α-自旋子能帶向上移動,體系重回HSC;增加電場到Eext=1.0 V/?時,體系又轉變為HM.

最后,研究垂直應變對異質結的磁電子特性的調控效應.仍以TS_m方式吸附的異質結為例,施加的應力如圖7(a)所示,其應變定義為:ε=d-d0,其中d和d0分別代表施加應變前后Sb 單層與WS2單層的層間距.為評估應力對異質結能量穩定性的影響,計算系統的應變能,其定義為: ΔES=ES-E0,其中ES(E0)為應變發生后(前)體系在FM 態的總能量,計算結果如圖7(b)所示.不難看出,施加應力后,系統能量上升,即結構的能量穩定性降低,但ΔES隨ε變化為一光滑的拋物線型,這說明在我們計算的應變范圍內(-0.5 ?≤ε≤0.5 ?),體系處于彈性形變,即Fe 原子與兩單層所成的化學鍵沒有斷開或重構的情況.我們計算的帶隙隨應變的變化也呈現在圖7(b),可以看出,在拉伸范圍內(ε＞0),帶隙下降,在ε=0.3 ?后,帶隙為0(HM或MM).而在壓縮范圍內(ε＜0),體系的帶隙上升.這說明應變能對體系的帶隙實施有效的調節.此外,圖7(b)也畫出不同應變下系統的磁相,即當應變滿足-0.5 ?≤ε≤0.3 ?時,體系保持HSC性質不變,而當應變滿足0.3 ?＜ε≤0.4 ?時,體系從HSC 轉變為HM,而取0.4 ?＜ε≤0.5 ?時,體系又變成MM.這說明應變能明顯調節磁性且獲得不同的磁相.

為了更清晰地展現應變對異質結磁電子性質的調控細節,圖7(c)-(f)給出ε=-0.3,0.2,0.35,0.4 ?時的能帶結構.與未施加應變時的能帶(見圖5(b)所示)相比較,我們發現ε=-0.3 ?時,能帶分布并未發生顯著變化(其他壓縮情況基本類似,未呈現),而ε=0.2,0.35,0.4 ?時,能帶分布發生了較為明顯的變化,因此,大致得出一個結論,即壓縮對整個能帶分布的影響較小,它只改變體系的帶隙;而拉伸應變,不僅能調節帶隙,而且對費米能級附近的能帶分布有較顯著的影響.這是由于,在施加應變之前,Fe 吸附在Sb/WS2層間,與Sb 原子和S 原子之間形成共價鍵結合在一起,而當施加壓力時,三者依然保持共價結合特性,因此體系的能帶結構不會發生顯著改變,而當施加拉力時,隨著層間距的增大,原共價結合的Fe,Sb 及S 原子不斷增加離子鍵成分,導致晶體場較大的改變,使能帶結構發生明顯改變,尤其是費米能級附近的能帶.此外,從圖7(b)-(f)可以清楚地看到,應變從ε=-0.5 ?到0.5 ?過程中,異質結的層間距單調增大,導致帶隙單調減小,成一反變關系,怎樣解釋這種現象? 如前所說,對于Fe 原子按TS_m方式吸附的異質結,α-自旋的最低導帶主要來源于WS2層的貢獻,而α-自旋的最高價帶主要來源于Fe 原子的貢獻(見圖5(e)),且Fe 原子失去電子,WS2層得到電子,所以存在一個從Fe 原子指向WS2層的內電場Ein.當異質結的層間距單調增大時,從Fe 原子到WS2層的電子轉移減少,導致Ein減弱,且Ein是Fe 原子到WS2層靜電勢能差的決定因素,所以這個靜電勢能差隨層間距增大單調變小,使最高價帶與最低導帶不斷靠近,即帶隙單調減小.

圖7 (a)施加的拉力與壓力示意圖;(b)應變能、帶隙及磁相隨應變變化;(c)-(f)ε=-0.3,0.2,0.35和0.4 ?時的能帶結構,其中圖(e)與圖(f)中綠色區域代表該部分的能帶放大圖Fig.7.(a)Schematic diagram of stretching and compressing heterostructure;(b)the strain energy,band gap and magnetic phase as versus strain;(c)-(f)band structure at ε=-0.3,0.2,0.35,and 0.4 ?,where the green region in panel(e)and(f)represent the enlarged partial band structure.

4 結論

我們構鍵Sb/WS2異質結,通過計算和比較結合能,確定最穩堆垛方式(S2),并進行系統研究.PBE 和HSE06 計算均表明: As 單層、WS2單層以及Sb/WS2異質結(S2)三者都為半導體,且構成Sb/WS2異質結后,其帶隙明顯變小.PBE 計算雖然低估帶隙,但對系統的電子特性能給出與HSE06計算基本類似的結果.考慮計算成本,僅利用PBE計算對Fe 原子吸附異質結誘發的磁特性進行了細節研究.計算的吸附能表明: TW,TS_m及VSb吸附是Fe 原子分別吸附于異質結下方、層間以及上方的最可能吸附位置,都能使異質結產生磁性,這是由于Fe 原子被吸附后其電子構型(VEC)擴展以及電荷轉移使得電子自旋重排所致,而電荷轉移的數量與Fe 原子相對附近原子的電負性密切相關.TW,TS_m吸附使異質結為磁性半-半導體(HSC),而VSb吸附使異質結為雙極化磁性半導體(BMS).特別是,計算的磁化能表明: TS_m具有最高的磁穩定性,在常溫下足以保持磁穩定性,而VSb的磁性在常溫下容易受到熱起伏的影響而轉為無磁狀態.量子調控使異質結產生豐富的磁性,特別是磁相的靈活改變,如施加外加電場可使異質結實現HSC,HM 及BMS 等磁相的轉換,應變則可使異質結發生HSC,HM 及MM 等磁相的轉換,同時使得異質結的帶隙隨層間距增大而單調減小.這些結果表明Fe 吸附的Sb/WS2異質結對于研發納米磁器件有潛在應用.