等離子體性質對磁泡的影響

彭國良 張俊杰 王仲琦 任澤平 謝海燕 杜太焦

1)(北京理工大學機電學院,北京 100081)

2)(西北核技術研究所,西安 710024)

利用三維混合模擬程序計算了大量超熱碎片離子在低密度背景等離子體中爆炸膨脹的過程.通過定量計算磁泡的變化過程和磁泡對碎片云運動的約束效果,分析了背景等離子體電荷密度、背景離子原子量、碎片離子荷質比等參數對磁泡的影響.計算結果表明,背景電荷密度對磁泡和碎片云的運動有重要影響.在碎片云擴張早期,背景離子原子量對磁泡擴張影響較小,但對后期碎片云的運動有一定影響.當碎片離子荷質比較小時,離子回旋半徑大于磁泡半徑,此時磁泡半徑較小,且磁泡無法約束碎片云.當碎片離子荷質比較大時,離子回旋半徑小于磁泡半徑,如果此時背景電荷密度較低,磁泡和碎片云的早期擴張幾乎不受碎片離子荷質比影響,但對系統后續演化有一定影響,如果此時背景電荷密度較大,碎片離子荷質比對磁泡和碎片云的運動有較大影響.

1 引言

大量超熱碎片離子在低密度背景等離子體中爆炸膨脹時,如果存在背景磁場,磁場中會產生磁泡(magnetic bubbles or diamagnetic cavities),即磁場強度極低的區域,此時碎片離子形成的碎片云,在一定條件下能被約束在磁泡內部.這一現象在高空核爆炸[1]、天體物理[2]和激光等離子體實驗[3]等領域廣泛存在.高空核爆炸產生的磁泡是形成晚期核電磁脈沖的重要機制,磁泡的發展過程對晚期電磁脈沖的強度有重要影響[4],爆炸產生的碎片云含有放射性元素,其運動狀態對大氣電離、人造輻射帶、極光等很多地球物理現象均有重要作用[5].天體物理和激光等離子體實驗中,磁泡與等離子體的Rayleigh-Taylor 不穩定性直接相關.因此研究磁泡在工程和學術領域都具有重要意義,也引起了很多學者們的關注[6].當碎片離子運動時,一部分能量傳遞給磁場,形成磁激波,另一部分傳遞給背景等離子體,導致背景等離子體運動.Berezin 等[7]的研究表明,碎片能量傳遞機制取決于阿爾芬馬赫數MA(碎片速度與阿爾芬波速度之比).當MA?1時,能量主要傳遞給磁場;當MA?1 時,能量主要傳遞給背景等離子體.對MA?1 的情況,Ripin等[8]忽略背景離子的影響,將磁壓等效為流體的壓力,利用能量守恒得到磁泡最大半徑計算公式,該公式沒有考慮磁泡實際的三維形狀,也沒有考慮各種耗散機制.Gisler 等[9]和Winske[10]針對三維形狀在Ripin 等[8]的基礎上各自給出了修正系數[11,12].修正的公式有助于估算磁泡尺寸的上限,但考慮到實際問題比較復雜,磁泡的發展歷程更多依賴實驗和模擬得到[13-16].在實際的高空核爆問題中,環境離子密度、碎片離子和環境離子的種類存在很大的不確定性,這種不確定性對磁泡和碎片云分布的定量計算均有一定影響.本文利用三維數值模擬方法研究了背景等離子體電荷密度、背景和碎片離子荷質比等因素對磁泡的影響,并分析了磁泡對碎片云的約束效果.

2 計算模型和方法

2.1 物理模型

以高空核爆炸問題引起的磁泡問題為例,爆炸碎片離子的典型速度約為1.5×106m/s,如用一價鐵離子等效碎片離子,地磁場典型值取0.3 G(1 G=10-4T),則對應的運動尺度(回旋半徑)約為數十千米量級,相應的電子運動尺度為米量級.流體的適用條件是網格尺度遠大于粒子自由程,故對網格尺度千米量級的問題,離子不能用流體描述,可采用PIC(particle-in-cell)模型描述;而電子可作為流體處理,這就是著名的混合模型[17-19].等離子體無碰撞近似滿足的條件為[20]

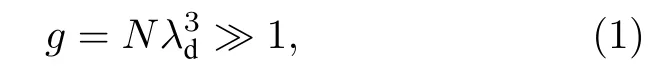
式中,g為等離子體參數,N為電子數密度,λd為德拜長度.

電中性近似需滿足的條件為[21]

式中,Δl為網格尺度.無質量電子近似滿足條件:

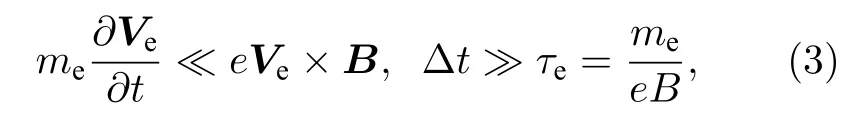
式中,Δt為時間尺度,τe為電子回旋時間,e為電子電荷,me為電子質量,Ve為電子的流體速度,B為磁場.

典型的高空核爆炸碎片云散開到千米尺度時,等離子體密度下降到 1×1012cm-3,則等離子體的德拜長度約為0.005 m,遠小于千米級網格尺度,故滿足電中性近似;等離子體參數g＞1×1011,滿足無碰撞近似;關心的時間尺度為0.1 s 級,遠大于電子回旋時間尺度0.1 ms 級,故滿足無質量電子近似.此時可以得到無碰撞離子的運動方程為

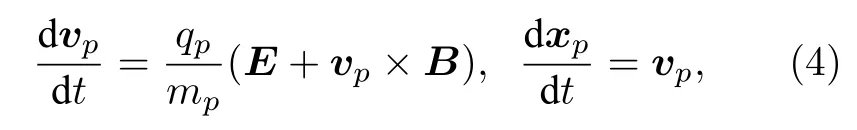
式中,v,q,m,x分別為宏粒子的速度、電荷量、質量和位置坐標;下標p代表第p個宏粒子;E和B為宏粒子感受到的電場和磁場.

若忽略電子的質量,由電子動量方程可得到電場的表達式

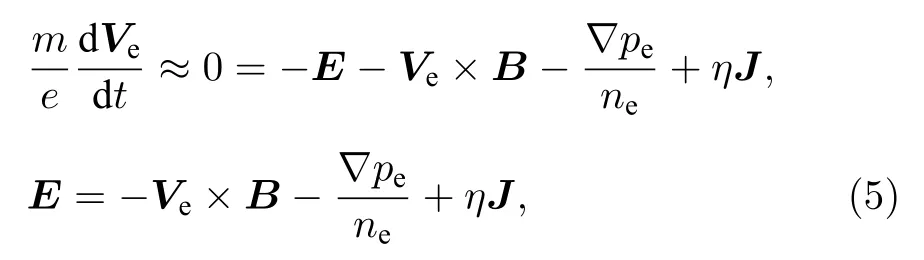
式中,ne為電子電荷密度,在電中性近似下等于離子電荷密度;pe為電子壓強;η為電阻.在電子溫度和密度較小時,可忽略電子壓力和電阻,此時電場的表達式進一步簡化為

其中,電子的流體速度可以由電流的定義式給出:

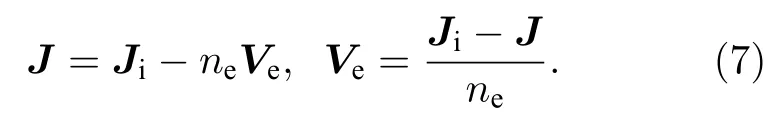
在電子流體速度遠小于光速時,滿足低頻Darwin近似,可忽略麥克斯韋方程的位移電流項,得到簡化的電磁場方程:

為便于計算,重新定義電磁場變量以消去磁導率常數μ0:

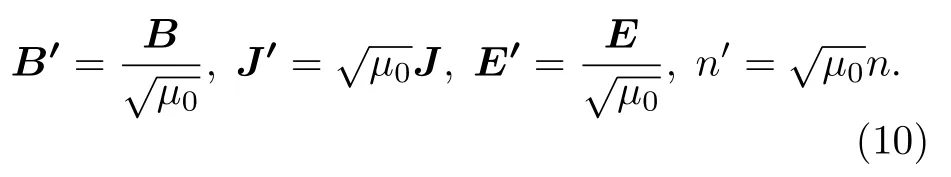
于是電磁場方程可寫為

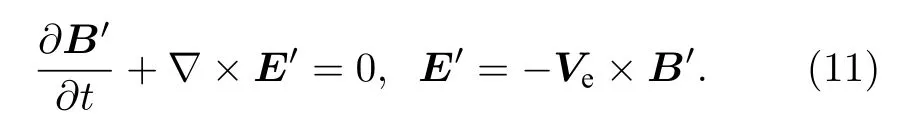
為保證計算的磁場散度為0,采用廣義拉格朗日乘子方法[22],方程(11)修正為

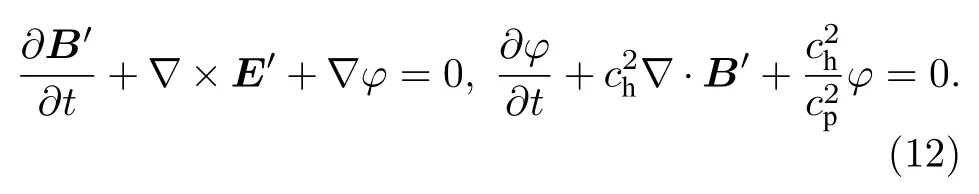
式中,ch和cp為控制參數,建議的取值可參考文獻[22].

2.2 計算格式

粒子運動方程采用Boris 時間推進格式[23]計算:

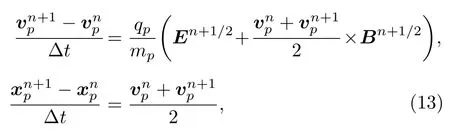
式中,上標n表示當前時間步,n+1 表示下一時間步.(5)式為線性方程組,求解可得到下一時刻宏粒子的位置和速度.記離子的電荷密度為ni和電流密度為Ji,則

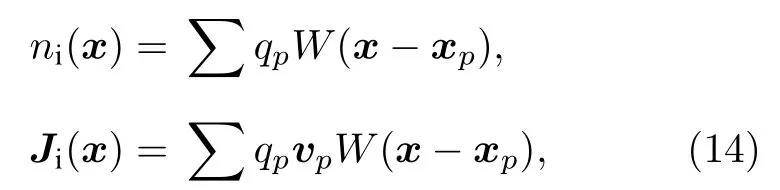
式中,W為權函數,可使用CIC(cloud-in-cell)權函數模型給出[24].

求解(11)式的空間積分采用有限體積格式,時間積分利用二階顯式龍格-庫塔方法求解,可得到電磁場隨時間的演化.

將場方程改寫為守恒格式:

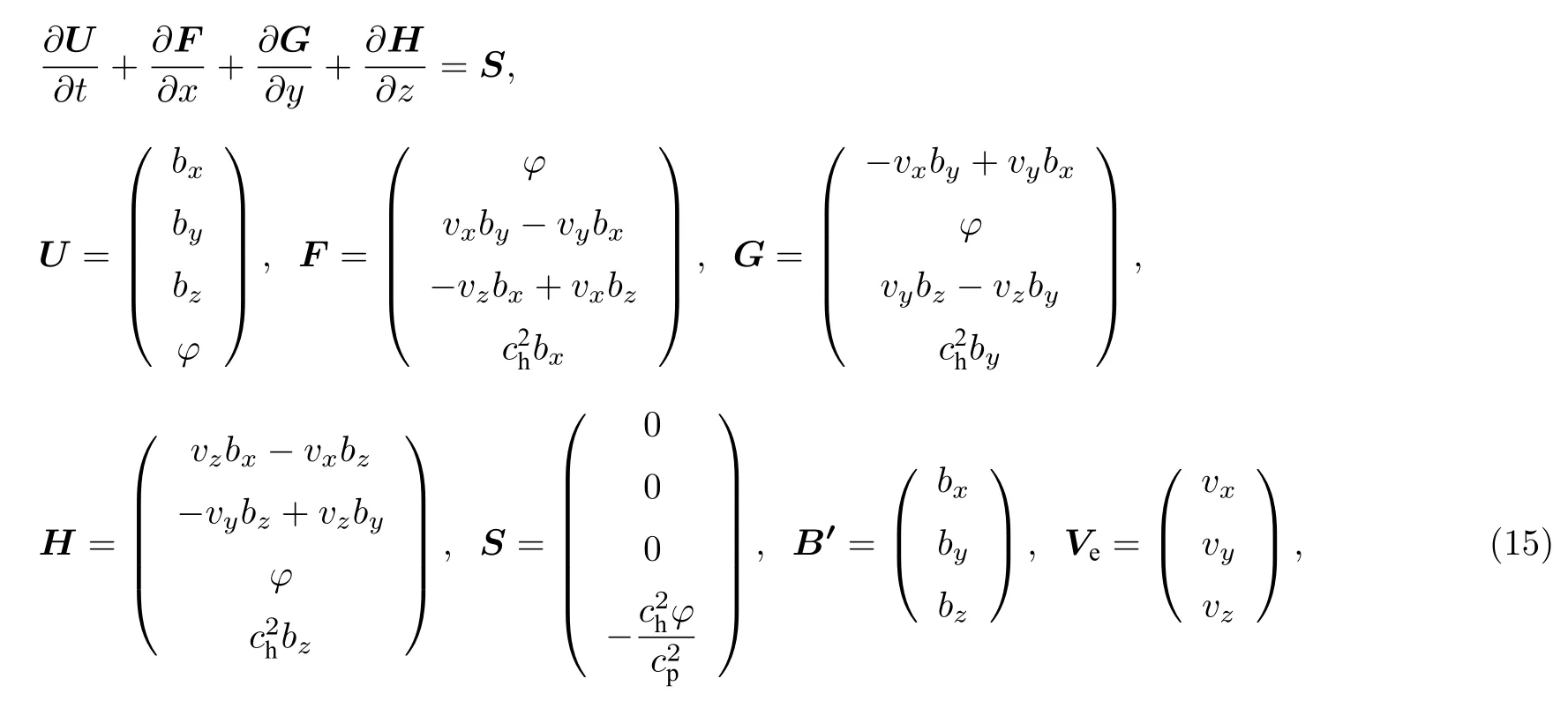
利用有限體積方法可以求解(15)式.含Van-Leer 限制器的二階守恒重構格式為[25]

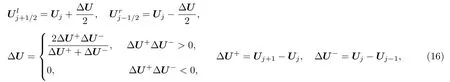
通量F,G,H用Lax-Friedrichs 格式計算[26].場變量時間推進格式用龍格-庫塔格式:

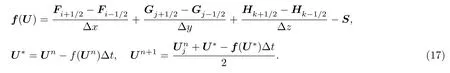
2.3 程序驗證

2.3.1 場方程求解器測試

電荷密度和磁場滿足的方程為

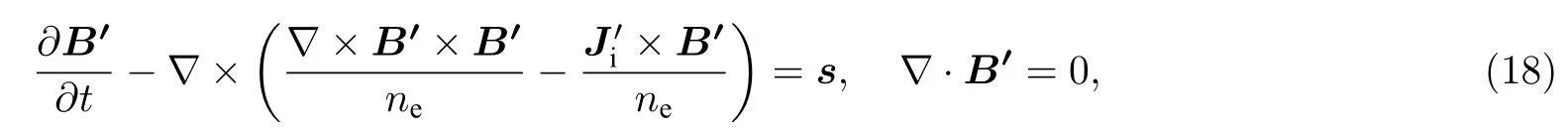
式中,s為磁場方程的配平源項,方程的一組人造解為

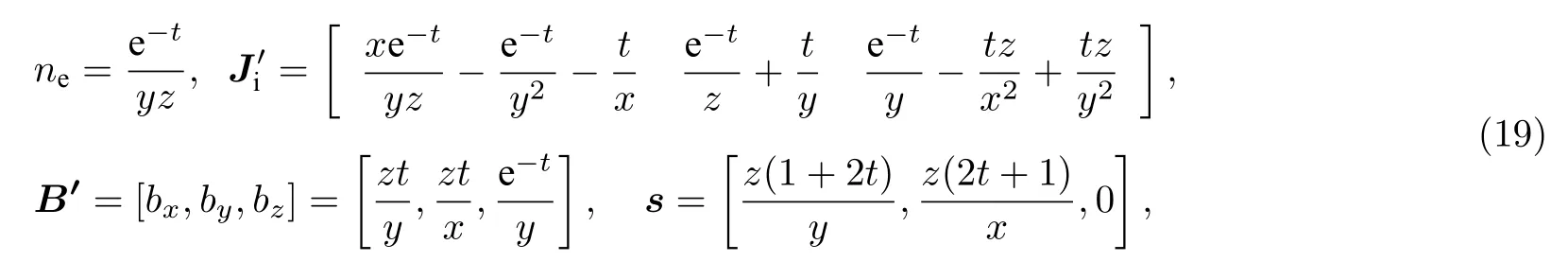
通過程序計算得到一組解Bc=,設置誤差函數為

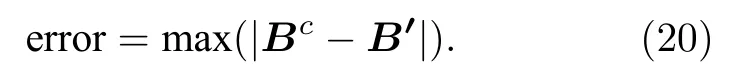
計算區域為 [0,1]3,網格數 10×10×10,CFL 數取0.25,計算的誤差隨時間的變化如圖1 所示.從圖1 可以看出,計算的磁場誤差很小,程序能正確模擬磁場的演化.

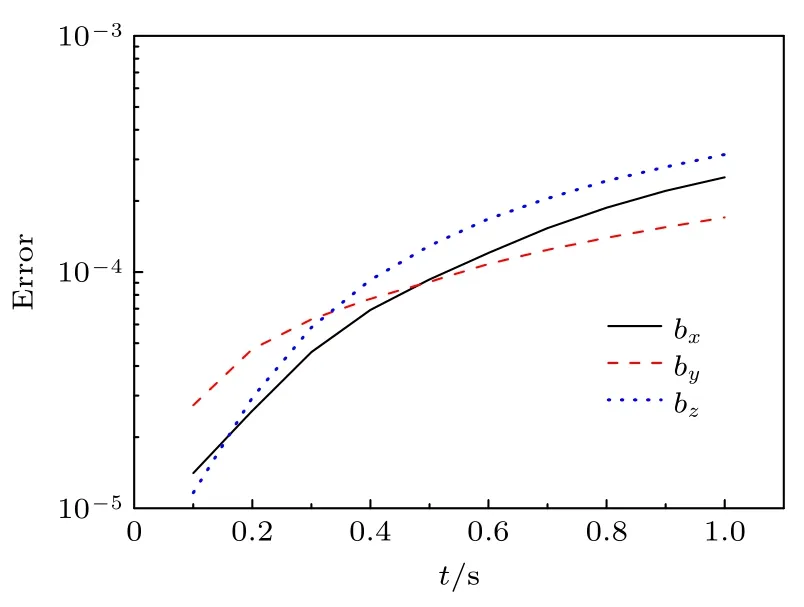
圖1 磁場誤差隨時間的變化Fig.1.Variation of magnet field variables error with time.

2.3.2 粒子求解器測試

考慮線性的粒子相對漂移問題.僅考慮時間微分,并假設兩種粒子均勻分布,因而所有的空間導數項為0,對應的速度方程可簡化為

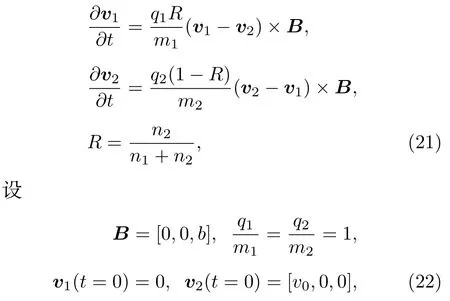
則問題的解析解為

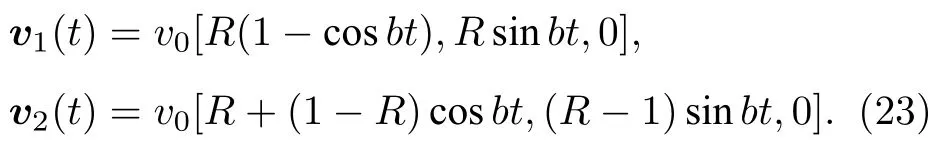
設置誤差函數為

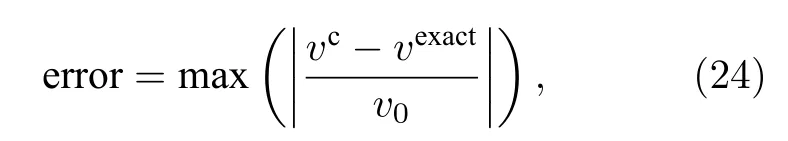
式中,上標c 表示程序計算值,exact 代表解析解.

程序計算中取b=2π,v0=5,R=1/2,計算區域為 [0,1]3,計算網格為 10×10×10,兩種宏粒子在每個網格上設置1 個,采用周期邊界條件,計算得到的誤差如圖2 所示.由于程序計算中保持嚴格的動量守恒,兩種粒子的誤差函數是一樣的,因此僅展示了類型1 粒子的誤差.可以看出,計算誤差很小,程序能正確計算粒子的運動.

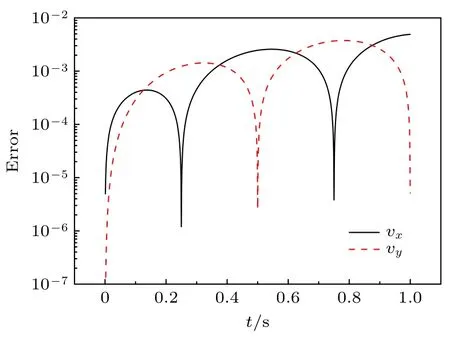
圖2 粒子速度誤差隨時間的變化Fig.2.Variation of particles velocity error with time.

3 分析與討論

Ripin 等[8]由能量守恒給出:

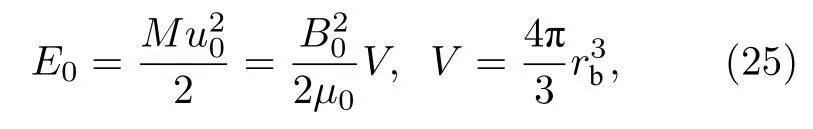
式中,E0為碎片總動能,M為碎片總質量,u0是碎片初速度,B0是背景磁場強度,V為磁泡體積,rb為最大磁泡半徑.(25)式給出的最大磁泡半徑是全部動能轉化為電磁能時磁泡總體積對應的等效半徑.實際上在有背景離子存在時,有部分碎片動能轉化為背景離子動能,磁泡半徑會小于(25)式給出的估計值.由能量守恒得到

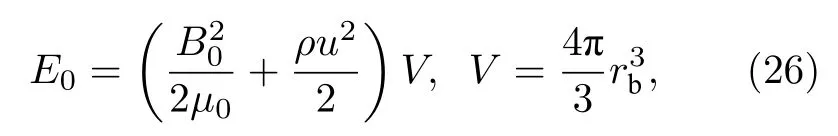
式中,ρ為背景離子密度;u為背景離子速度,由于動量守恒的限制,一般不會超過碎片初速度.當背景離子密度很大、背景離子速度等于碎片初速度時,得到文獻[13]中提到的等質量半徑:

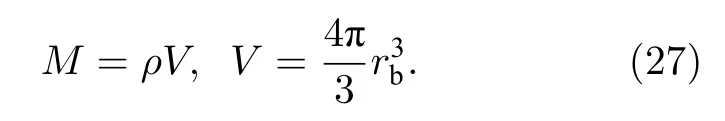
這里M為碎片離子的總質量.實際的背景離子速度尚無解析結果,需要借助數值模擬計算磁泡半徑.數值計算得到磁場分布后面臨的問題是如何計算磁泡半徑.Winske 等[6]指出磁泡是磁場中場強極小的區域(|B|≈0),由于對極小沒有明確定義,這個定義公式在實際應用時存在不確定性.為定量分析等離子性質對磁泡和碎片云分布的影響,需對磁泡半徑和碎片云分布給出定義.

典型的磁泡云圖(即磁場強度大小密度云圖)如圖3 所示,在圖3 中,爆炸發生在中心位置,隨著碎片離子向外擴展,逐漸形成磁場強度較低的區域.垂直于磁場的截面一般為圓形,其半徑與碎片初始速度垂直于背景磁場方向的分量有關,垂直初速度分量越大,磁泡半徑越大;平行于磁場的截面為紡錘形.這里定義磁泡半徑Rb為垂直于磁場方向的最大半徑:

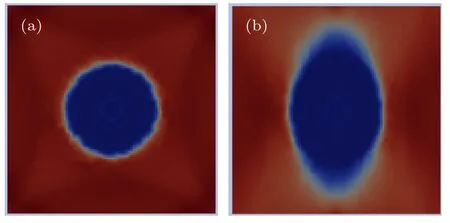
圖3 磁泡云圖(a)垂直于背景磁場的截面;(b)平行于背景磁場的截面Fig.3.Magnetic bubbles contour:(a)Cross section perpendicular to background magnet;(b)cross section parallel to background magnet.

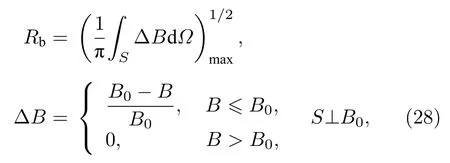
式中,B0為背景磁場,S為垂直于背景磁場的平面.碎片云分布的定義可以參照文獻[13]的作法,即將包含98%碎片離子的區域定義為碎片離子擴展半徑Rd:

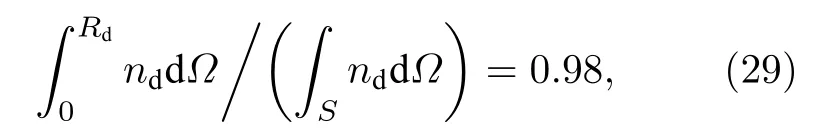
式中,nd為碎片云離子數密度.碎片離子的平均半徑Ravg定義為

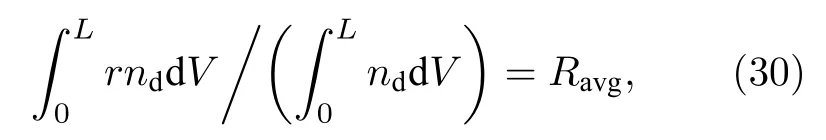
其中L通常取計算區域的大小.另外為便于比較,定義歸一化的磁泡半徑δb、碎片云擴散半徑δd和碎片云平均半徑δavg:

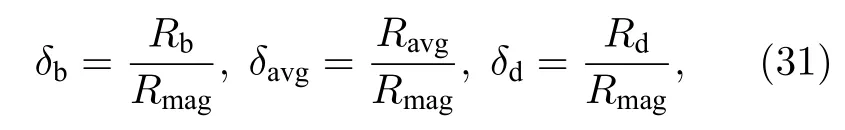
式中,等能量最大磁泡半徑Rmag的計算公式為[10]

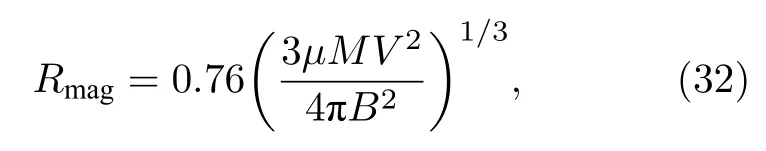
其中,MV2/2 為碎片離子的初始總動能.

計算中設碎片離子和背景離子的電荷數為1,背景離子原子量記為Ab,碎片離子原子量記為Ad,背景電荷密度記為N.設碎片離子總質量M=1 kg,初始均勻分布在半徑1 km 的球內,初始速度滿足麥克斯韋分布,且平均值vd=1000 km/s,背景磁場B0=0.3 G,則Rmag≈52.7 km,阿爾芬馬赫數為

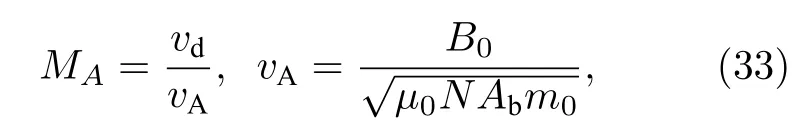
其中,m0為單位原子質量.設計算區域為[-100,100]×[-100,100]×[-60,60].

3.1 背景電荷密度的影響

將背景離子原子量Ab取為16,碎片離子原子量Ad取56,背景電荷密度N分別取1010,1011,1012和1013m-3,對應的阿爾芬馬赫數分別為0.61,1.93,6.09 和19.3.其他條件不變,計算背景電荷密度對磁泡半徑和碎片云分布的影響.

圖4 給出了不同背景電荷數密度下磁泡半徑隨時間的演化.從圖4 可以看出,背景等離子體的電荷數密度越大,最大磁泡半徑越小,磁泡的發展越慢.從磁流體角度分析,背景等離子體密度越高,由碎片離子傳遞給背景離子的能量越多,從而導致磁泡擴張變得困難,磁泡半徑變小.另外,背景等離子體密度增大后導致碎片離子平均速度變慢,相應的磁泡發展速度也變慢.從圖4 還可以看到: 背景電荷密度較小時,磁泡首先快速擴張到最大值,然后收縮,做周期運動;當背景電荷密度較大時,磁泡擴張到一定大小后,可以較長時間保持相對穩定狀態.

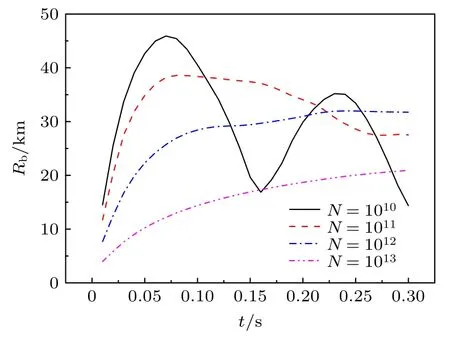
圖4 不同背景電荷數密度下磁泡半徑隨時間的演化Fig.4.Magnetic bubbles radius vs. time under different background charge number density.

圖5 給出了不同背景電荷數密度下歸一化磁泡半徑和碎片云半徑隨時間的變化.從圖5 可以看出碎片云在磁泡中進行周期運動,當背景電荷密度較小時,碎片云的運動周期較大,頻率較低.由于低電荷密度下磁泡本身也進行周期運動,碎片云的運動會受磁泡運動的影響,其周期(約0.17 s)也與磁泡運動周期(約0.16 s)相當.電荷密度較大時,磁泡的發展較為穩定,碎片云的運動周期主要受碎片離子的回旋周期的影響.從圖5 還可以看到,不同背景電荷數密度下碎片云的最大擴展半徑都在1.2Rm左右,變化較小,但平均半徑差別較大,這可能暗示碎片云的最大半徑主要由不與背景等離子體相互作用的碎片離子在背景磁場中的回旋運動決定.當背景電荷密度較小時,碎片云的平均半徑與磁泡半徑基本相當,這表明碎片云的分布更多集中在磁泡邊緣,隨磁泡的運動而運動;背景電荷密度較大時,碎片云的平均半徑在磁泡內振蕩,這表明碎片云在磁泡邊緣和中心來回振蕩,這與文獻[15]的現象一樣.

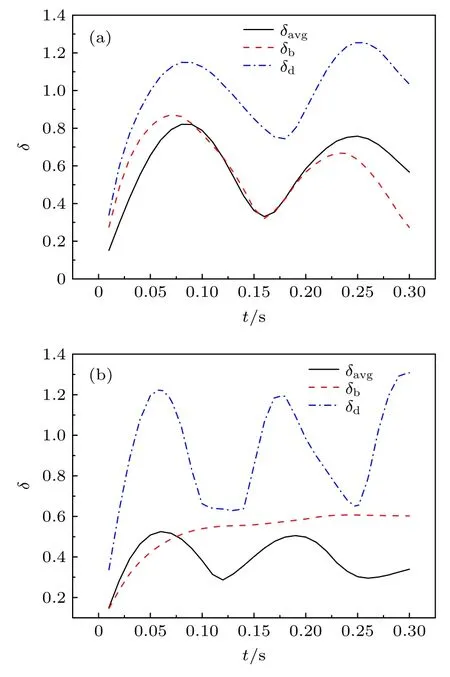
圖5 歸一化磁泡半徑和碎片云半徑隨時間的變化(a)N=1×1010 m-3;(b)N=1×1012 m-3Fig.5.Normalization debris radius and magnetic bubbles radius vs.time:(a)N=1×1010 m-3;(b)N=1×1012 m-3.

3.2 背景離子原子量的影響

改變背景離子的原子量會影響背景離子的質量密度和阿爾芬波速,還會影響背景離子的回旋半徑和周期.取背景電荷密度N分別為1010和1012m-3,背景離子的原子量Ab分別取16,32 和64,碎片離子原子量Ad取56,其他條件不變,計算此時背景離子原子量對磁泡半徑和碎片云分布的影響.

圖6 所示為不同背景離子原子量下磁泡半徑隨時間的變化.由圖6 可知,背景離子原子量較大時,早期磁泡發展速度變慢,高背景電荷密度下,這種影響更顯著.從圖6 還可以看到,低背景電荷密度下,背景離子原子量較大時,最大磁泡半徑較小,振蕩的幅值也較小;高背景電荷密度下,背景離子質量的變化對最大磁泡半徑的影響較小.

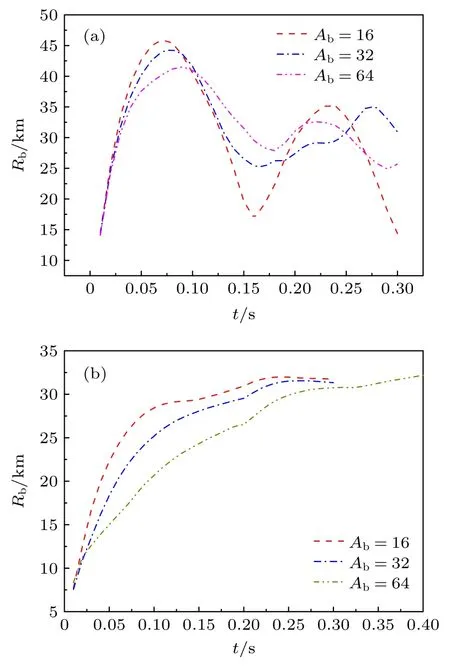
圖6 不同背景離子原子量下磁泡半徑隨時間的變化(a)N=1×1010 m-3;(b)N=1×1012 m-3Fig.6.Magnetic bubbles radius vs. time with different background ion atomic weight:(a)N=1×1010 m-3;(b)N=1×1012 m-3.

圖7 給出了N=1010m-3時不同背景離子原子量下碎片云半徑隨時間的變化.從圖7 可以看到,低背景電荷密度下,背景離子原子量越大,碎片云的平均半徑和擴展半徑的最大值都會減小.第1 個擴張-收縮周期內不同背景離子原子量對碎片云的分布影響較小,第1 個周期后影響較大.

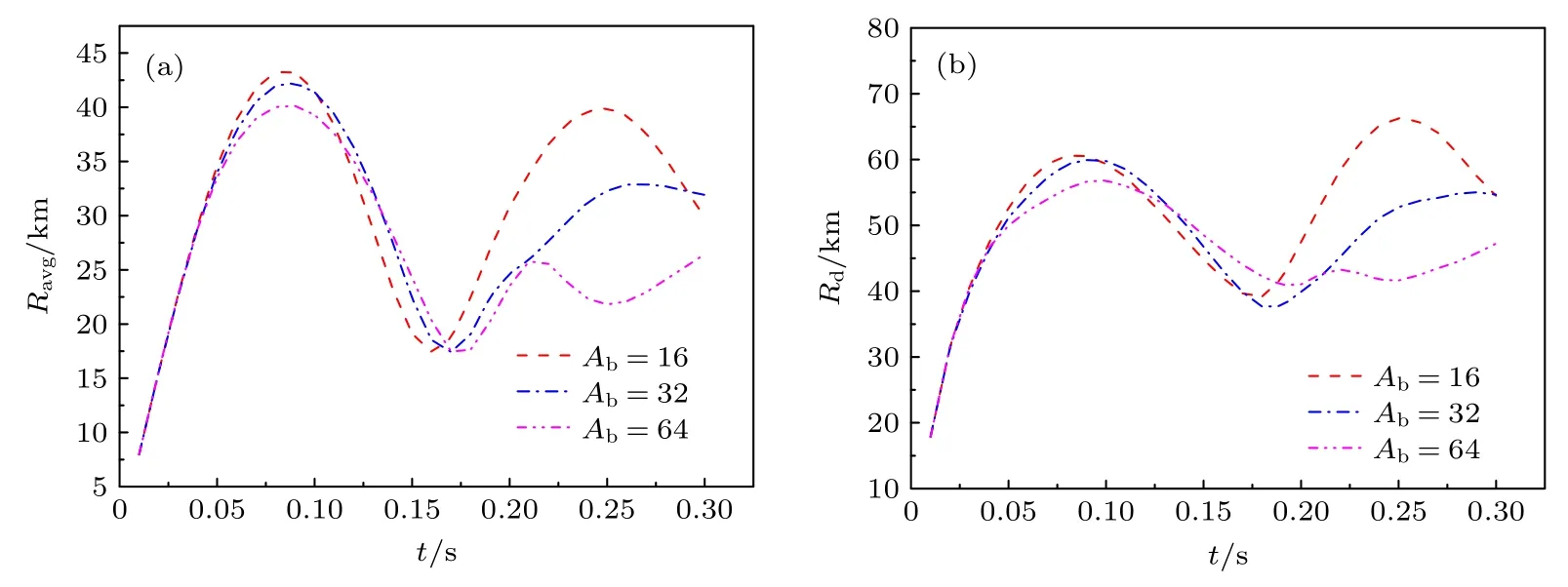
圖7 N=1×1010 m-3 時不同背景離子原子量的碎片云半徑隨時間的變化(a)Ravg;(b)RdFig.7.Debris radius vs.time at N=1×1010 m-3 under different background ion atomic weight:(a)Ravg;(b)Rd.

圖8 所示為N=1012m-3時不同背景離子原子量下碎片云半徑隨時間的變化.由圖8 可知,高背景電荷密度下,背景離子原子量對碎片云第一次擴張的影響很小,對碎片云開始收縮后的影響較大,Ab值越大,第1 個波谷的碎片云半徑越小.這表明背景離子的原子量對碎片云半徑的影響主要在背景離子密度較低時顯現.

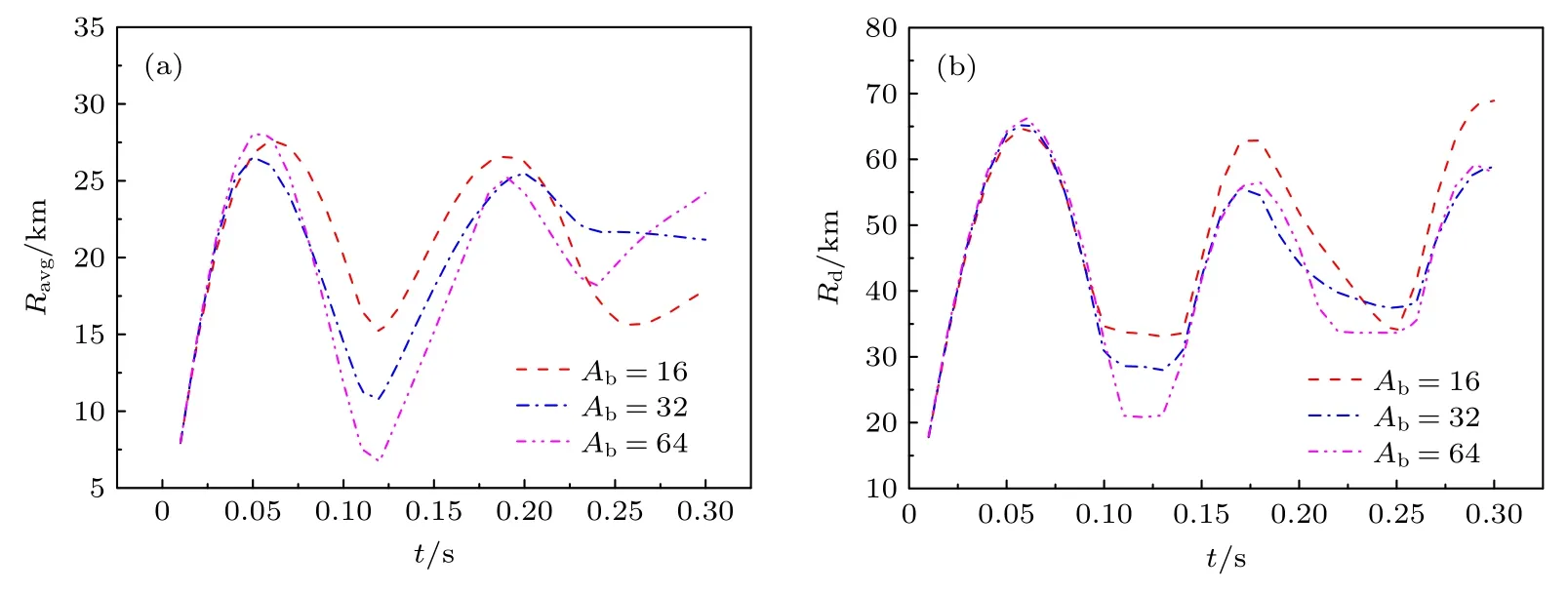
圖8 N=1×1012 m-3 時碎片離子半徑隨時間的變化(a)Ravg;(b)RdFig.8.Debris radius vs.time at N=1×1012 m-3 under different background ion atomic weight:(a)Ravg;(b)Rd.

3.3 碎片離子荷質比的影響

固定電荷數,增大碎片離子的原子量相當于減少荷質比.在總質量一定時,改變碎片離子的荷質比會影響碎片離子的總電荷數,還會影響碎片離子的回旋半徑和周期.取背景等離子體電荷密度分別為1010和1012m-3,背景離子的原子量Ab為16,碎片離子原子量Ad分別取為14,28,56 和235,對應的回旋半徑分別為4.84,9.68,19.4 和81.3 km,其他條件不變,計算背景電荷密度對磁泡半徑和碎片云分布的影響.

圖9 所示為不同碎片離子原子量下磁泡半徑隨時間的變化.由圖9 可知,無論電荷密度高低,如果碎片離子原子量過大,荷質比過小,則離子回旋半徑大于最大磁泡半徑,此時最大磁泡半徑會顯著減小.對離子回旋半徑小于最大磁泡半徑的情形,當背景離子電荷密度較低時,荷質比對最大磁泡半徑影響較小,但對磁泡后續的收縮過程有一定影響,Ad越大,磁泡收縮時波谷半徑越小,磁泡的周期也會略微延長;當電荷密度較大時,Ad越大、荷質比越小,最大磁泡半徑越大.

圖10 和圖11 分別給出了低背景電荷密度和高背景電荷密度時不同碎片離子原子量下碎片云半徑隨時間的變化.可以看出,當碎片離子原子量較大時,碎片云平均半徑明顯超出磁泡半徑,擴展半徑很快超出計算域,這表明磁泡約束失效,部分碎片離子已逃逸出計算域.因此只考慮磁泡約束有效的情形.低電荷密度下,碎片離子原子量對碎片云的第1 次擴張的影響很小,但對后續的振蕩過程有影響;Ad增大時,振蕩周期變長,幅值增大.高電荷密度下,碎片離子質量增大時,碎片云最大平均半徑和擴展半徑都會增大,振蕩周期變短,幅值增大.

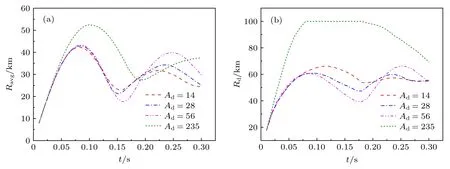
圖10 N=1010 m-3 時不同碎片離子原子量下碎片云半徑隨時間的變化(a)Ravg;(b)RdFig.10.Debris radius vs.time at N=1010 m-3 under different debris ion atomic weight:(a)Ravg;(b)Rd.

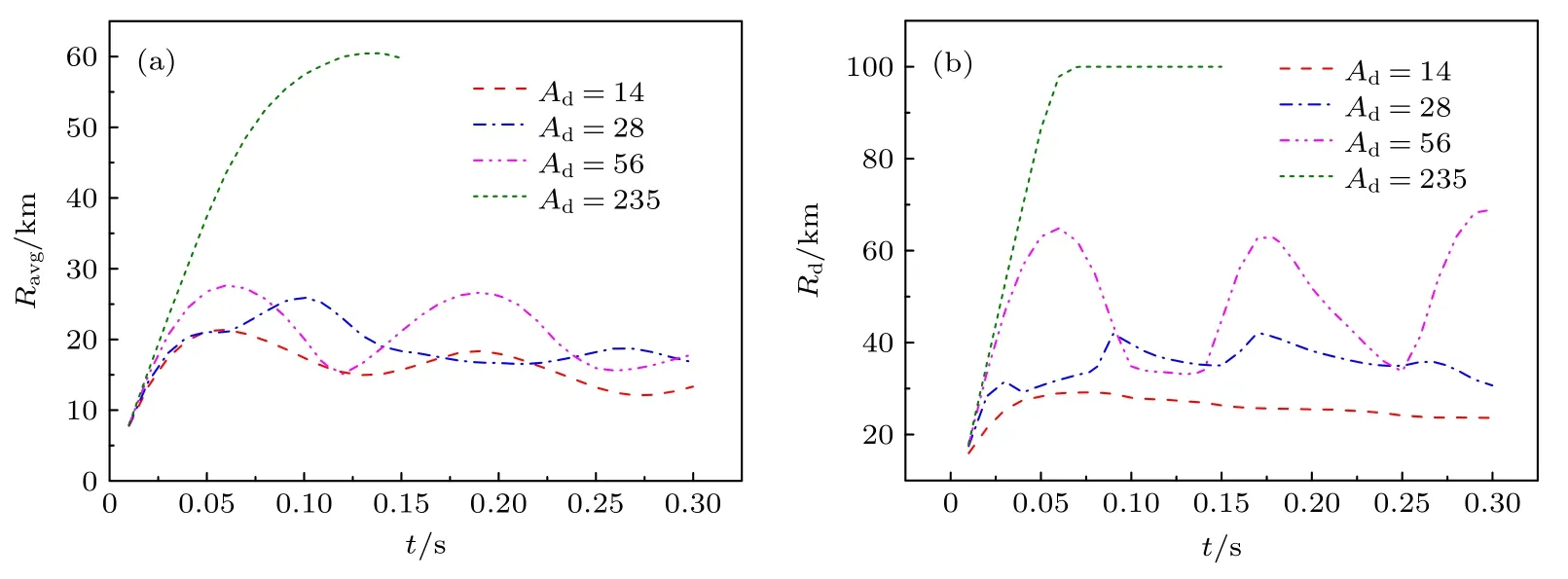
圖11 N=1×1012 m-3 時不同碎片離子原子量下碎片云半徑隨時間的變化(a)Ravg;(b)RdFig.11.Debris radius vs.time at N=1×1012 m-3 under different debris ion atomic weight:(a)Ravg;(b)Rd.

圖12 所示為歸一化碎片云平均半徑和磁泡半徑隨時間的變化.由圖12 可知,在低電荷密度下,不同碎片離子原子量的碎片云平均半徑與磁泡半徑相當,表明碎片云一直集中在磁泡邊緣.高電荷密度下,在磁泡穩定期,碎片離子原子量較小的碎片云平均半徑遠小于磁泡半徑,表明碎片云集中在磁泡內部;碎片離子原子量較大的碎片云平均半徑的波峰與磁泡半徑相當,波谷遠小于磁泡半徑,表明碎片云在磁泡邊緣與內部振蕩,這與Winske 等[13]在二維計算得到的結論一致.

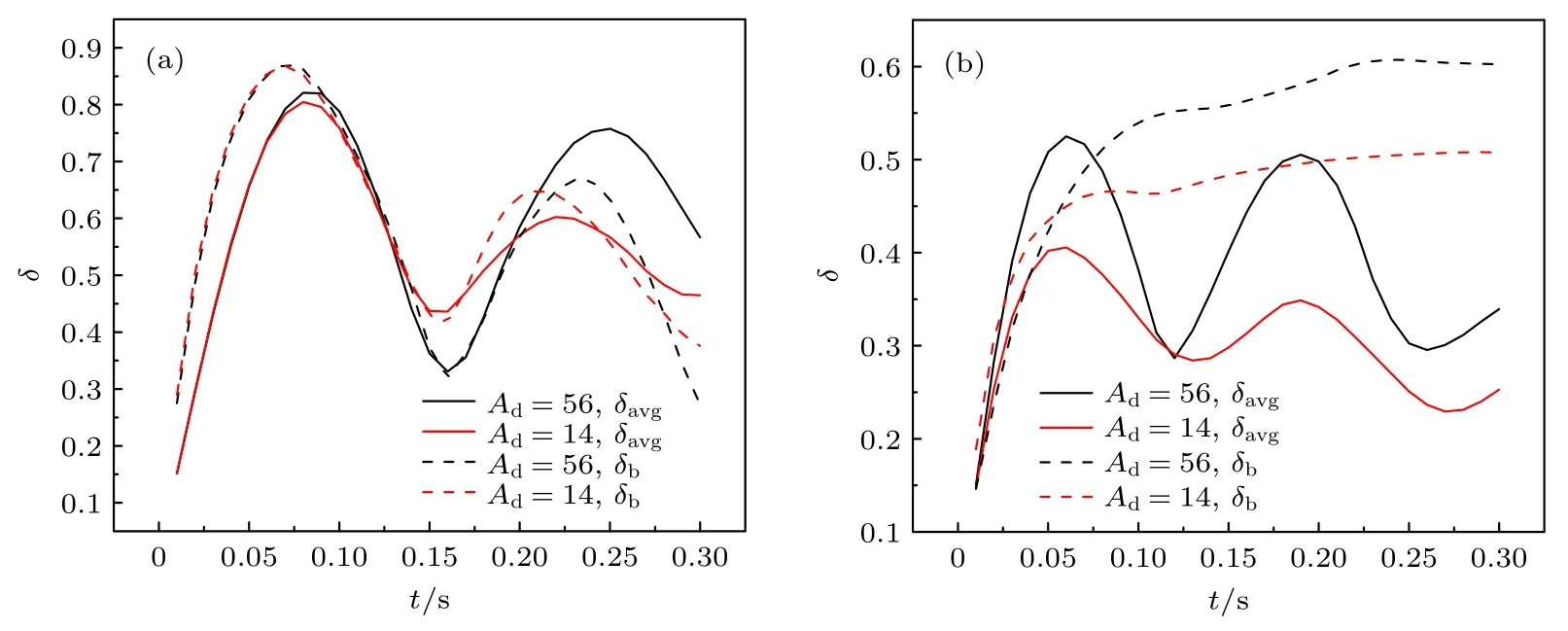
圖12 不同碎片離子原子量下歸一化碎片云半徑和磁泡半徑隨時間的變化(a)N=1×1010 m-3;(b)N=1×1012 m-3Fig.12.Normalization debris radius and magnetic bubbles radius vs.time under different debris ion atomic weight:(a)N=1×1010 m-3;(b)N=1×1012 m-3.

4 結論

本文用三維混合粒子模擬程序研究了大量超熱碎片離子在含背景磁場的低密度背景等離子體中爆炸膨脹過程.通過定義磁泡半徑、碎片云擴張半徑和平均半徑,研究了背景等離子體的電荷密度、背景離子原子量和碎片離子荷質比對磁泡發展過程的影響,并分析了磁泡對碎片云的約束效果.計算結果表明,背景等離子體的電荷數密度越大,最大磁泡半徑就越小,磁泡的發展越緩慢;當背景電荷密度較小時,磁泡做周期振蕩,碎片云集中在磁泡邊緣并跟隨磁泡做周期運動.如果背景電荷密度較大,當磁泡擴張到一定大小后,其可以較長時間保持相對穩定狀態,此時碎片云在磁泡內部和邊緣振蕩.如果保持背景等離子體電荷密度一定,當背景離子原子量增大時,磁泡發展速度變慢,該現象在背景電荷密度較高時會更顯著.在低背景電荷密度下,當背景離子原子量較大時,最大磁泡半徑較小,磁泡振蕩的幅值也較小;在高背景電荷密度下,背景離子原子量的變化對最大磁泡半徑的影響較小.背景離子原子量對碎片云早期的擴張影響不大,但對后期的碎片云分布有一定影響.當碎片離子荷質比過小時,離子回旋半徑大于磁泡半徑,此時磁泡半徑會顯著減小,且磁泡無法約束碎片云.當碎片離子荷質比較大時,如果此時背景離子電荷密度較低,碎片離子荷質比對最大磁泡半徑影響較小,但對磁泡后續的收縮過程有一定影響;當背景離子電荷密度較大時,碎片離子荷質比越小,最大磁泡半徑越大.低背景等離子體電荷密度下,碎片離子荷質比對碎片云早期擴張的影響很小,但對后續的振蕩過程有影響.高背景等離子體電荷密度下,荷質比較大時,碎片云集中在磁泡內部;荷質比較小時,碎片云在磁泡邊緣和內部之間振蕩,碎片離子荷質比減小后,碎片云最大平均半徑和擴展半徑都會增大,振蕩周期變短,幅值增大.