基于多孔金膜的太赫茲導模共振生化傳感特性仿真*

楊澤浩 劉紫威 楊博 張成龍 蔡宸 祁志美?

1)(中國科學院空天信息創新研究院,傳感技術國家重點實驗室,北京 100190)

2)(中國科學院大學電子電氣與通信工程學院,北京 100049)

仿真設計了一種高靈敏度太赫茲(THz)導模共振生化傳感結構.該結構由硅棱鏡、介質薄膜和多孔金膜組成,多孔金膜同時作為THz 導波層和生化分子富集層,能夠增強THz 導模與生化分子間的相互作用,從而提高探測靈敏度.當采用棱鏡全反射方法激勵THz 橫電(TE)或橫磁(TM)導模后,多孔金膜的吸收使得THz 反射頻譜出現尖銳的共振吸收峰,由此可確定THz 導模的共振頻率及其對液體折射率和生化分子吸附量的靈敏度.調節介質層的厚度和折射率可進一步提高上述THz 傳感結構的靈敏度和品質因數.在45°入射角下的仿真結果指出,TE 和TM 導模的共振頻率隨著液體折射率或生化分子吸附量的增大而線性變化,TM 導模的折射率靈敏度可高達13.42 THz/RIU,品質因數達到167.70/RIU,TE 導模對液體折射率的靈敏度小于TM 導模,但對分子吸附量的靈敏度大于TM 導模,究其原因是TE 導模透出多孔金膜的消逝場比TM導模弱.

1 引言

太赫茲(terahertz,THz)技術是近二十年來發展最快的技術之一,THz 波在電磁波譜中位于微波波段與紅外波段之間,是頻率為0.1-10 THz的電磁波.THz 波在電磁波譜中特殊的位置使其具有一些獨一無二的性質,例如光子能量低,因此不會對生物樣品造成損傷,同時其穿透性很強,更重要的是THz 頻段覆蓋了許多生物大分子的振轉能級[1,2],利用該性質可以對大分子進行“指紋譜”檢測.這些特性使得THz 傳感技術在物質表征、公共安全、生物醫學和生化檢測等領域具有良好的應用價值[3-5].目前,THz 傳感技術還未能在痕量生化物質探測方面獲得廣泛的應用,這主要受限于現有常規THz 傳感技術靈敏度的不足,以及THz 源和探測器發展的滯后.為了提高THz 探測靈敏度,科研人員提出了THz 表面等離激元共振傳感技術,設計制備了不同周期性結構的THz 超表面,這些超表面具有顯著的THz 場增強效應,起到了極大的增敏作用[6-10].但現有的THz 超表面傳感技術的靈敏度仍然沒有高到足以探測痕量生化物質.

利用SPR 的場增強效應可以提高THz 傳感器件的靈敏度,因此THz 技術與SPR 技術的結合在生化檢測方面有著很大的應用前景.THz 波段的SPR 并不是可見光波段SPR 的簡單移植,廣泛應用于可見光波段SPR 結構中的金、銀等貴金屬在THz 波段不再直接適用,這是因為貴金屬等離子體頻率在紫外波段,與THz 波段相距較遠,THz波段下貴金屬的介電常數太高,且趨膚深度很小,THz 波段的貴金屬類似于完美導體,因此THz 波很難直接在金屬-介質表面激發SPP,而且THz 表面等離子體波在金屬-介質界面處束縛能力較弱,這就導致了其場增強效應很弱.通過深入的研究,科學家提出了各種替代光滑金屬表面的方案,例如摻雜半導體[11,12]、石墨烯[13]和亞波長周期型陣列結構[14,15]等.其中研究最為廣泛的是亞波長周期型陣列結構,自2004 年,Pendry 團隊[16]發現穿孔的高導電性表面可以激發人工表面等離激元(spoof surface plasmon polariton,SSPP)起,科研人員開始對該結構進行了深入研究.亞波長金屬孔陣列“透射增強”(extraordinary optical transmission,EOT)效應對周圍介電環境十分敏感,利用該特性已經對化學制劑[17]、蛋白質[18,19]、分子結合過程[20]、DNA[21]、同位素[22]、異形體[23]和有機溶劑[24]等物質進行探測.但是與THz 波長相比,待測分子的吸收截面很小,導致分子和THz 波輻射之間的相互作用相當弱.另一方面,受限于探測器敏感特性差、THz 源衍射光斑直徑大等問題[25],透射式THz傳感技術的檢測靈敏度不高,因此研究人員將研究方向著眼于基于棱鏡全反射耦合的Otto 和Kretschmann 結構來激發THz-SPP,通過棱鏡滿足相位匹配條件將THz 波耦合到SSPP,從而解決了THz 波與物質間相互作用弱的問題.2013 年,Ng等[26]使用Otto 結構對液氮、汽油、甘油等物體進行了探測,并在理想條件下獲得了 0.47 THz/RIU 的靈敏度.2020 年,Huang 等[27]對亞波長光柵結構的THz-SPR 相位檢測方法進行了研究,并得到了一種高測量精度的THz 相位跳變型傳感器.在上述報道中,基于亞波長金屬周期結構的透射式和棱鏡反射式SSPP 傳感系統均受限于復雜的制備工藝,并且其靈敏度較低.

為了解決上述問題,本文提出了一種基于多孔金膜/介質薄膜非周期性結構的THz 導模共振生化傳感結構,通過棱鏡耦合的方式滿足波矢匹配條件,在THz 波段下激發THz 導模.與傳統的平行板波導(parallel-plate waveguide,PPWG)不同[28],本文將多孔金引入到太赫茲傳感領域,利用其可填充待測物和富集小分子的能力,增大導模與待測物的作用范圍,打破了光滑致密金屬膜表面敏感特性的限制,從而提高了導模傳感結構的靈敏度.本文首先介紹了THz 導模共振傳感結構和原理,分析了介質層最佳厚度及其折射率對THz 波到THz導模耦合效率的影響.在此基礎上,研究了導模共振結構對待測物質折射率變化的響應情況,進而得到該結構對不同物質的探測靈敏度和品質因子,并對其進行了對比分析.最后,本文還驗證了利用多孔金膜富集小分子的能力可以對溶液中低濃度小分子進行較高靈敏度的探測.

2 THz 導模共振傳感結構的結構設計及傳感機理研究

2.1 結構設計及原理

基于多孔金膜/介質薄膜的非周期性結構THz導模共振生化傳感結構如圖1 所示,該結構很容易與太赫茲時域光譜(THz time-domain spectroscopy,THz-TDS)技術結合來得到出射光的光譜信息.用于滿足波矢匹配條件的硅棱鏡(n=3.416)與多孔金膜之間夾有一層介質層來增強金屬-介質界面對表面波的束縛能力[29,30],以實現局域場增強效應.入射角θ在滿足全反射條件時(θ≥θc=arcsin(n2/n1)),在高折射率硅棱鏡和介質層界面處會發生全反射,產生倏逝波,當倏逝波的波矢與表面模波矢相等時,可以將倏逝波的能量耦合到表面模.與常規的SPR 傳感結構不同,我們沒有使用可見光波段傳統的光滑致密金膜或者常用于THz波段帶有亞波長周期結構的金膜,而是將多孔金膜引入到該結構當中.

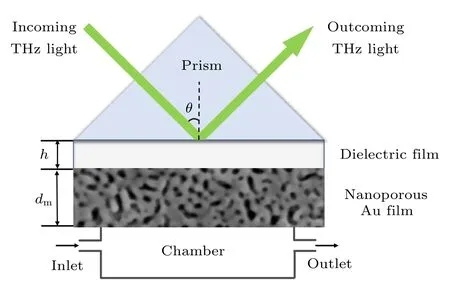
圖1 THz 導模共振生化傳感結構示意圖Fig.1.Schematic diagram of the THz waveguide resonance biochemical sensing structure.

多孔金膜與亞波長金屬周期結構不同,通常情況下,多孔金膜孔隙尺寸(約為 50—100 nm)[31]遠小于探測波長,因此在THz 波段下可以等效為一種均勻介質,即:εx=εy=εz=εm,εm是多孔金膜的等效介電常數.此外,它也有別于傳統致密金膜,由于多孔結構的存在,可以通過調節孔隙率和填充物來改變多孔金膜的等效折射率nm,根據Bruggeman 公式[32]可以得到其等效折射率nm的表達式:

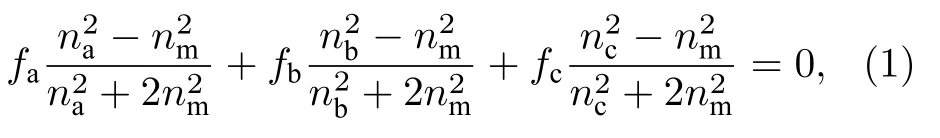
式中,fa,fb,fc分別是多孔金骨架、孔內介質和孔內吸附小分子所占的體積分數,且fa+fb+fc=1.在孔內未富集小分子情況下,fc=0.na,nb,nc分別對應著三者的折射率.其中,金的折射率na是個復數,可以通過計算其介電常數的實部和虛部而獲得.基于Drude 模型,金屬介電常數的實部(εr)和虛部(εi)作為電磁波角頻率的函數可以表示為

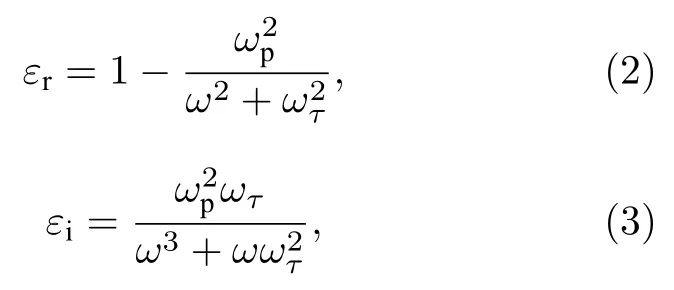
式中,ωp和ωτ分別為金屬的等離子體頻率和阻尼頻率,對于金而言,ωp=1.367×1016rad/s,ωτ=4.072×1013rad/s[33].多孔金膜的引入,可以使待測物填充到孔隙中,同時借助其大比表面積的特性達到富集小分子的作用[34,35],從而充分利用場增強效應來探測溶液中低濃度的生物小分子.

為了能夠更加規范地評價本文中導模共振結構的性能,通過靈敏度和品質因數(figure of merit,FOM)這兩個參數來對其進行量化分析:

1)頻率檢測型THz 導模共振傳感結構的靈敏度可以通過共振頻率(fr)的改變量 δfr與待測物折射率改變量(δn)或吸附小分子體積分數改變量(δfc)的比值來定義:

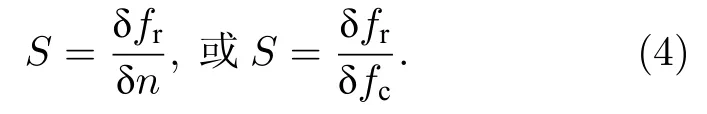
2)FOM 可以用于對導模共振結構綜合性能的評判,其定義為該結構靈敏度S與反射頻譜半高峰寬(FWHM,ΔλFWHM)的比值,即:

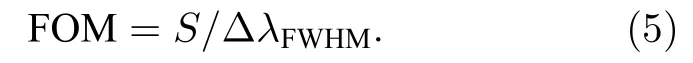
2.2 仿真及傳感機理分析

多孔金膜的介電常數依賴于頻率,并且對fr和反射頻譜的性質有著很大的影響,其實部決定了fr的移動,而虛部會影響反射頻譜的FWHM.由(4)式和(5)式可知,頻移和FWHM 影響著導模共振結構探測的靈敏度和FOM,這兩個參數直接決定著該結構的探測性能.除了頻率,多孔金膜的介電常數也依賴于孔隙率和待測物質的折射率,通過調節金銀合金中各成分的比例和腐蝕時間,可以得到不同孔隙率的多孔金膜.由Bruggeman 公式計算可得在空氣條件下,不同孔隙率的多孔金介電常數εNPG實部和虛部隨頻率的變化情況,如圖2 所示.從圖2 可以清楚地看到,為了解決THz波段下貴金屬介電常數虛部過高的問題,需要較大孔隙率的多孔金,通過研究發現多孔金膜孔隙率在0.7 附近可以滿足介電常數實部遠遠大于虛部的條件,這表明在該條件下多孔金膜有能力在THz 波段下支持緊束縛的表面波[36].而當孔隙率超過0.7,多孔金介電常數虛部過小,實部占據了主導地位,導致共振吸收作用減小,難以產生尖銳的共振吸收峰,因此本文的仿真均以孔隙率p=0.7 為前提進行研究.

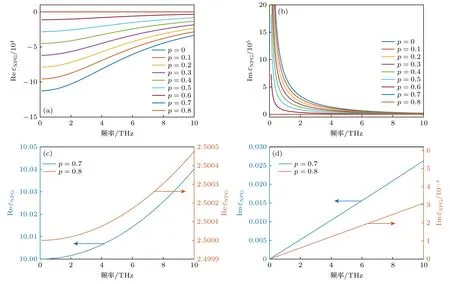
圖2 (a)不同孔隙率情況下,多孔金介電常數εNPG 實部隨頻率的變化;(b)不同孔隙率情況下,多孔金介電常數εNPG 虛部隨頻率的變化;(c)孔隙率為0.7 和0.8 時,多孔金介電常數εNPG 實部隨頻率的變化;(d)孔隙率為0.7 和0.8 時,多孔金介電常數εNPG 虛部隨頻率的變化Fig.2.(a)Variation of real part of εNPG as a function of frequency for different porosity;(b)variation of imaginary part of εNPG as a function of frequency for different porosity;(c)variation of real part of εNPG as a function of frequency for different porosity p=0.7 and 0.8;(d)variation of imaginary part of εNPG as a function of frequency for different porosity p=0.7 and 0.8.

在此基礎上結合2.1 節推導的等效介質近似,可以使用菲涅耳公式對多孔金膜界面上傳播的表面模式進行分析.菲涅耳公式給出了入射波、反射波和透射波之間振幅和相位的關系.透射系數t和反射系數r不僅取決于入射角度,還與入射波的偏振態有關.

1)TM 偏振光(偏振方向平行于入射面),其反射系數r和透射系數t可以表示為

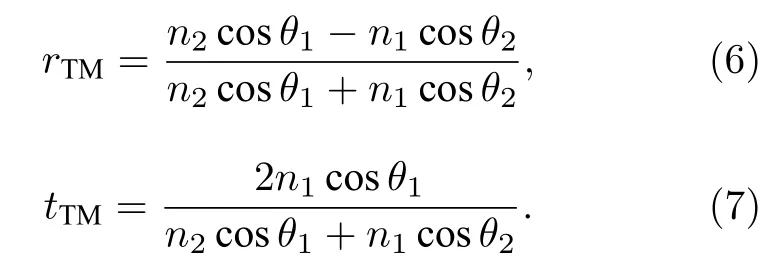
2)TE 偏振光(偏振方向垂直于入射面),其反射系數r和透射系數t可以表示為

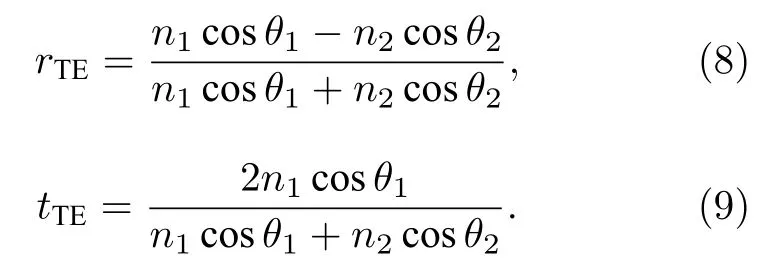
如圖1 所示,該導模共振結構可以近似為一個由棱鏡、介質層、多孔金膜和待測物組成的四層結構,其反射系數為

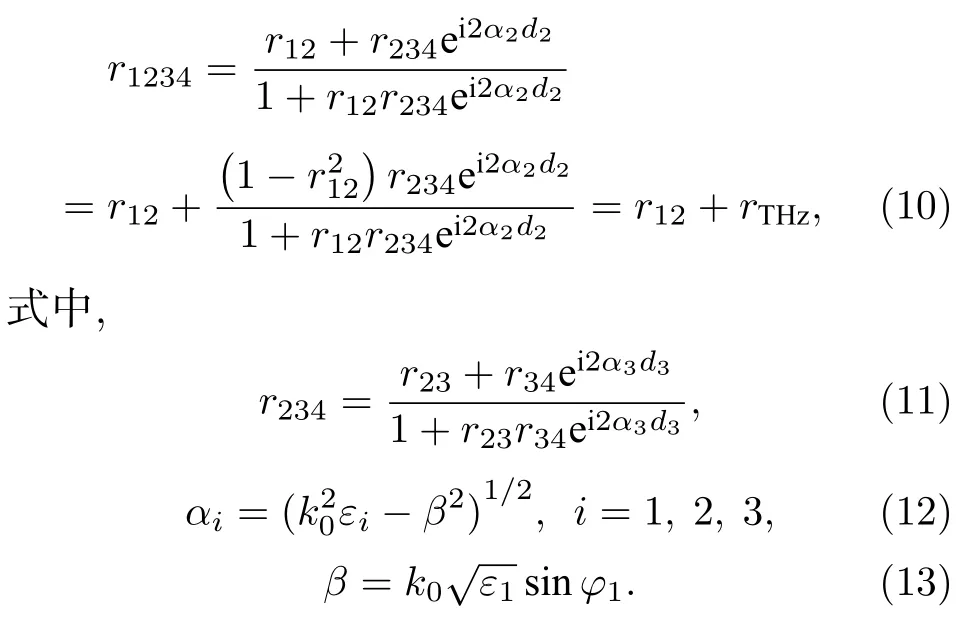
r12,r23,r34和rTHz分別為棱鏡-介質層、介質層-多孔金膜、多孔金膜-待測物界面和THz 導模的反射系數,d2和d3分別是介質層和多孔金膜的厚度,而ε1,ε2和ε3分別是棱鏡、介質層和多孔金膜的介電常數.最終得到四層介質結構的反射率為

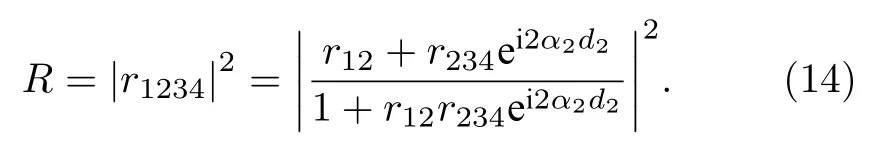
基于菲涅耳公式計算得到該模型TM 偏振光的反射率和相位曲線如圖3(a)所示,可以清楚地看到,反射率最小值出現在頻率為 1.996 THz 的位置,并伴隨著相位的突變.TE 模式通過上述公式同樣可以得到相似的結果,只是結構參數、共振頻率和靈敏度略有不同,為了統一,文中2.2 和3.1 節的仿真均以TM 偏振光為前提計算得到.為了進一步驗證該結構的可行性,使用基于有限元分析方法的COMSOL multiphysics 軟件(使用Floquet周期邊界條件和默認網格劃分)計算多孔金膜在該共振頻率下的場分布情況,其中介質層厚度h=13 μm,多孔金膜厚度dm=10 μm.在計算過程中,使用到了前文所述的Drude 模型來對金膜的色散分布進行計算,多孔金的等效折射率可以通過(1)式求得,從而仿真得到如圖3(b)所示的電場分布.可以清楚地看到,電場集中分布于多孔金膜和待測物質、介質層的交界面處,這說明該結構具有支持THz導模在其表面傳播的能力.同時,因為多孔金膜對表面波的束縛作用,所以在該界面處有很強的場增強效應,這是對樣品進行高靈敏檢測的重要保障.

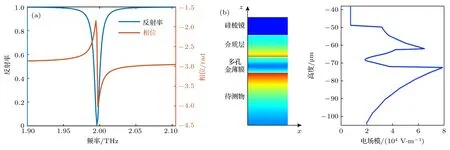
圖3 TM 模式下,(a)在介質層折射率 nd=1,厚度 h=13 μm,多孔金孔隙率為0.7 且厚度 dm=10 μm 時,頻率-反射率曲線及其頻率-相位曲線;(b)在介質層折射率 nd=1,厚度 h=13 μm,多孔金孔隙率為0.7 且厚度 dm=10 μm 時,該結構在頻率為1.996 THz 情況下的電場強度二維分布Fig.3.In TM mode:(a)Frequency-reflectivity curve and frequency-phase curve for a dielectric layer with refractive index nd=1,thickness h=13 μm,nanoporous gold film with porosity of 0.7 and thickness dm=10 μm;(b)two-dimensional distribution of the electric field strength of this structure,at 1.996 THz,for a dielectric layer with refractive index nd=1,thickness h=13 μm,nanoporous gold film with porosity of 0.7 and thickness dm=10 μm.

3 THz 導模傳感特性研究及性能改善

3.1 介質層厚度及折射率對耦合效率的影響

通過反射頻譜不僅得到了準確的共振頻率,還發現了介質層厚度h和折射率nd影響著THz 波到THz 導模的耦合效率,當反射率R=0 時耦合效率最高.為了進一步提高導模共振結構的精度和準確性,本節將對介質層厚度h及其折射率nd對耦合效率的影響進行深入的研究.在第2 節的基礎上,首先對介質層厚度的影響進行了研究,得到不同厚度情況下的反射頻譜,如圖4(a)所示.從圖4(a)可以看到,隨著介質層厚度h的增加,反射率會逐漸變小,并且先達到一個最小值,此后反射率會隨著厚度h的增加而越來越大.這說明在該結構中,存在一個最佳的介質層厚度hopt來使得THz 波到THz 導模的耦合效率達到最高.除此之外,隨著介質層厚度h的增加,共振頻率也會稍稍藍移.而在達到最佳厚度之后,隨著厚度的增加,反射率最小值變大的趨勢比頻移現象明顯得多,這說明當介質層厚度很大時,表面模成為多孔金膜的本征共振模式,耦合效率受到棱鏡的影響較小.圖4(c)(自左向右)分別是介質層厚度為9,13 和17 μm情況下的能量密度時間均值,比較三個仿真結果可以看出,在最佳厚度13 μm 的情況下,能量主要約束在多孔金膜之中,而在非最佳厚度的情況下,能量逐漸向兩側擴散.這可以通過倏逝波場與THz 導模場重疊范圍來解釋,當介質層厚度較小時,很大一部分的倏逝波會被金膜表面反射,而當厚度較大時,倏逝波則無法到達THz 導模場的范圍,在這兩種情況下兩個場的重疊范圍較小,因此造成能量向金膜兩側擴散的現象.在最佳厚度hopt的條件下,兩個場的重疊部分最大,使得倏逝波模場與THz導模場的耦合效率最高.為了進一步確定介質層厚度對導模共振結構靈敏度和精度的影響,分別對不同介質層厚度(厚度h范圍為5-21 μm)的傳感結構進行了仿真,得到如圖4(b)所示的介質層厚度對導模共振結構靈敏度和精度的影響.從圖4(b)可清楚地看到,折射率靈敏度隨著介質層厚度的增大而逐漸減小,但變化量很小,對該結構探測靈敏度的影響較小.但是介質層厚度會對導模共振結構的FOM 產生很大的影響,首先,FOM 會隨著厚度的增加明顯提升,在最佳厚度hopt處達到最大,之后FOM 會隨著厚度的增加稍稍降低.由此可知,為了提高THz 波到THz 導模的耦合效率和檢測精度,在最佳厚度hopt條件下進行探測是很有必要的.如圖4(d)所示,當耦合效率達到最大時,r12=1.0e-i2.95,rTHz=0.95ei0.13,兩個反射系數的振幅幾乎相等,相位差接近π,使得反射光強近似為零,因此反射率的最小值可以看作是由棱鏡-介質層反射波與THz 導波通過相消干涉得到的,這種干涉受到很多因素的影響,例如入射角、棱鏡的折射率和介質層的折射率及厚度等.

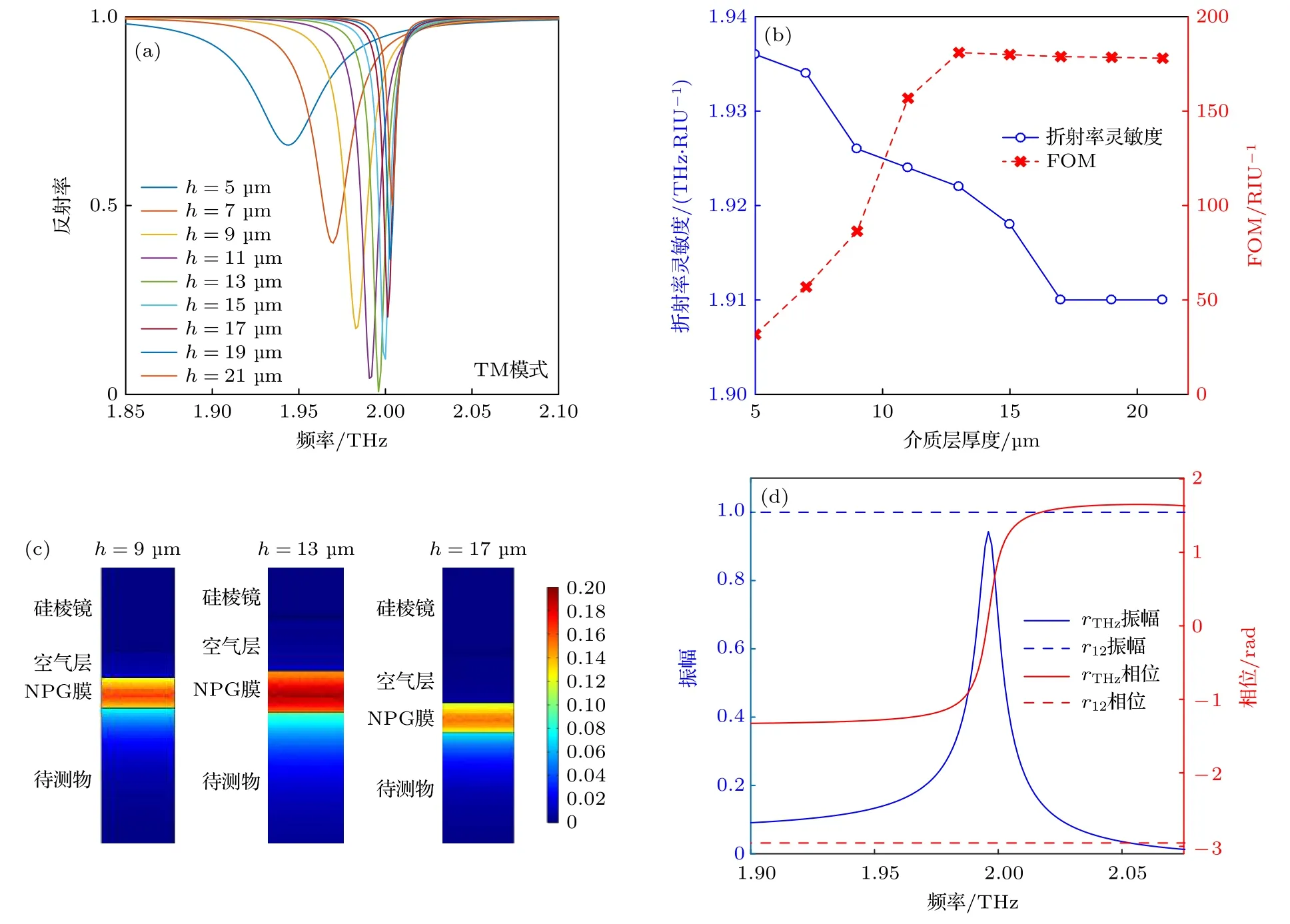
圖4 TM 模式下,在介質層為空氣(nd=1)時,(a)不同介質層厚度h 條件下的頻率-反射率曲線;(b)不同介質層厚度h 條件下折射率靈敏度和FOM 的變化;(c)三張圖(自左向右)分別是介質層厚度為9,13 和17 μm 情況下的能量密度時間均值(單位J/m3);(d)當介質層折射率 nd=1,厚度 h=13 μm 時,r12和rTHz 的振幅及其相位隨頻率的變化Fig.4.In TM mode,for a dielectric layer with refractive index nd=1,(a)frequency-reflectivity curves for different dielectric layer thicknesses h.(b)Variation of refractive index sensitivity and FOM for different dielectric layer thicknesses h.(c)The three pictures(from left to right)show the time-average energy density distribution at h=9,13,17 μm,respectively.(d)The variation of the amplitudes and phases of r12 and rTHz with frequency for a dielectric layer with refractive index nd=1,thickness h=13 μm.

除了介質層的厚度,其折射率nd也是影響導模共振結構靈敏度和精確度的重要因素之一,分別對介質層折射率nd為1,1.06,1.13,1.19,1.25,1.31,1.38,1.44 和1.5 的情況進行仿真,得到如圖5(a)所示的反射頻譜.由圖5(a)可以清楚地看到,隨著nd的增大,共振頻率會發生紅移,因此可以通過設計不同折射率的介質層來選擇工作頻段.除此之外,反射頻譜的最小值也會隨之增加,可以通過改變介質層的厚度得到不同折射率nd情況下的最佳耦合效率,如圖5(b)所示.從圖5(b)可以清楚地看到,當介質層折射率nd變為1.25 和1.5 時,介質層最佳厚度hopt分別增大到 19 μm和27 μm.如前所述,耦合效率是由反射波與THz 導波相消干涉所決定的,所以當介質層折射率增大時,需要更大介質層厚度來滿足干涉相消的條件,從而實現最高的耦合效率.為了進一步分析介質層折射率對導模共振結構靈敏度和FOM 的影響,分別對不同介質層折射率的傳感結構進行了仿真,得到如圖5(c)所示的折射率對導模共振結構靈敏度和FOM 的影響.從圖5(c)可以清楚地看到,折射率靈敏度隨介質層折射率的變化與隨介質層厚度的變化相似,也會隨著折射率的增大稍稍降低.但是在非最佳介質層厚度情況下(同為13 μm),FOM 隨著介質層折射率的增大而明顯變小,這會降低導模共振結構的探測精度.仿真結果指出當介質層厚度處于最佳值時,FOM 大幅提高,這有利于提高該結構的探測精度.

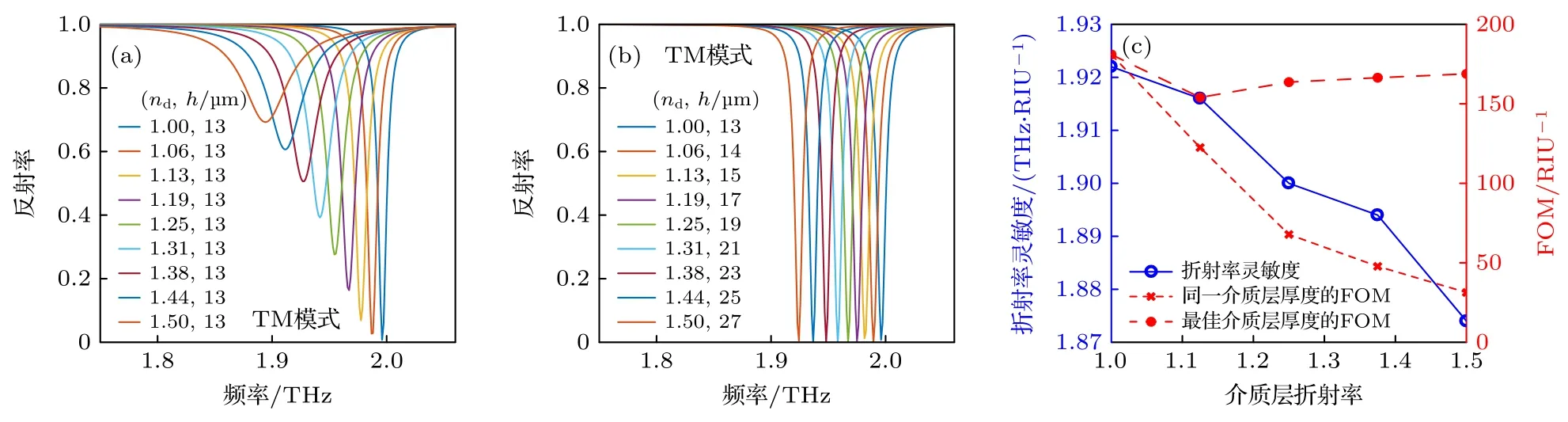
圖5 TM 模式下,(a)在介質層厚度 h=13 μm 條件下,介質層折射率 nd 不同時的頻率-反射率曲線;(b)在不同介質層折射率nd 和相應的最佳介質層厚度情況下的頻率-反射率曲線;(c)在介質層厚度 h=13 μm,不同介質層折射率 nd 條件下,折射率靈敏度和FOM 的變化及各自最佳介質層厚度情況下的FOMFig.5.In TM mode,(a)simulated reflectivity spectra for the same dielectric layer thicknesses h=13 μm and different dielectric layer refractive indices nd;(b)simulated reflectivity spectra for the respective optimum dielectric layer thicknesses hopt in different dielectric layer refractive indices nd;(c)in the case of dielectric layers with different refractive indices nd,variations in refractive index sensitivity and FOM for the same thickness h=13 μm and for the respective optimum dielectric layer thickness hopt,respectively.

通過上述研究發現當介質層厚度和折射率與最佳情況出現偏離時,會引起THz 波到THz 導模耦合效率的降低和FWHM 的增大,從而導致反射率的增大和FOM 的降低,使得傳感精度大大降低,所以找到所需波段對應的最佳介質層參數尤為重要.

3.2 待測物質與導模共振結構靈敏度的關系

3.2.1 待測物質折射率與靈敏度的關系

在前文中,通過仿真證明了本文提出的導模共振結構可以支持THz 導模的傳播,并且具有很強的場增強效應,這意味著該結構在用于生化傳感時具有高靈敏度的特性.本節以此為基礎,首先研究了待測物為水溶液時,該結構對周圍折射率環境變化的靈敏度及品質因數.為了獲得該結構的折射率靈敏度,選取了一些不同折射率的溶液(n=2.10,2.15,2.20,2.25,2.30),并且分別使用TM 和TE 兩種模式來進行仿真,兩種模式的反射頻譜如圖6(a)和圖6(b)所示.可以觀察到隨著待測物折射率的變大,共振頻率產生了明顯的紅移,說明該結構產生的THz 導模對周圍折射率環境變化是敏感的.此外,隨著待測物折射率的增大,共振曲線的FWHM稍有變寬且谷值逐漸變大,這是因為待測物折射率n的改變影響了導模的色散關系,從而減少了導模場和倏逝波場的重疊范圍.因此,在給定的結構條件下,待測物折射率與最佳折射率差距越大,耦合效率越低.為了獲得該結構的靈敏度,通過線性擬合可以得到如圖6(c)所示的折射率-共振頻率關系.當待測物質為不同折射率溶液時,在TM 模式下,該導模共振結構的靈敏度高達 1.92 THz/RIU,同時FOM 值高達 180.98 RIU-1;而在TE 模式下,該結構的靈敏度為 1.79 THz/RIU,同時FOM 值為55.45 RIU-1;可以清楚地看出在不同折射率溶液條件下,TM 模式的靈敏度和FOM值均優于TE 模式.從圖6 可以明顯觀察到,TE模式的共振頻率高于TM 模式,這是因為在該模型中TE 模式的有效折射率低于TM 模式,因此需要更大的共振頻率來滿足TE 模式較低的有效折射率.

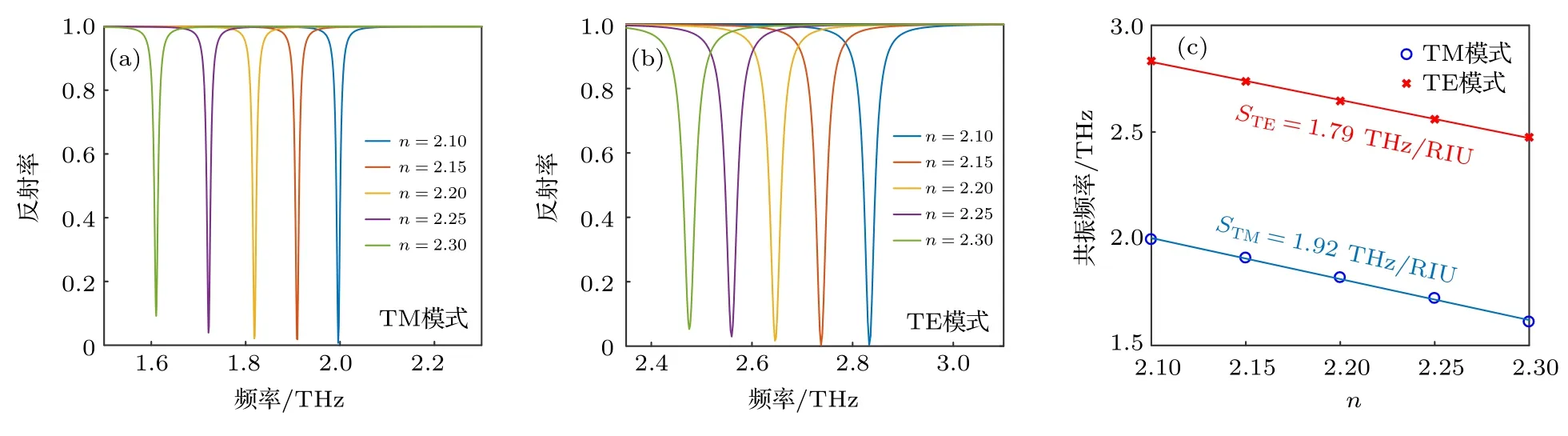
圖6 待測物為不同折射率溶液時,(a)TM 模式下,頻率-反射率曲線;(b)TE 模式下,頻率-反射率曲線;(c)在TM 和TE 模式下,折射率-共振頻率的線性擬合曲線Fig.6.(a)Reflectivity spectra for different refractive indexes of solutions in TM mode;(b)reflectivity spectra for different refractive indexes of solutions in TE mode;(c)refractive indexes of solutions-resonance frequency linear fitting curve for different refractive indexes of solutions in TM and TE mode.

為了驗證該結構具有寬動態探測范圍的特點,即可以對較大折射率范圍內的待測樣品進行探測.使用該導模共振結構對氮氣(n=1)、汽油(n=1.41)、乙醇(n=1.45)和液態石蠟(n=1.49)[37]進行仿真,得到不同待測物對應的共振頻率,分別為6.834 THz(氮氣,n=1),3.476 THz(乙醇,n=1.45)和1.996 THz(水,n=2.10).同時可以得到介質層最佳厚度及其靈敏度,如圖7 所示(汽油、乙醇和液態石蠟折射率接近,靈敏度變化可以忽略不計,因此圖中只給出氮氣、乙醇和水的數據).從圖7 可以清楚地觀察到,隨著待測物質折射率的變小,共振頻率會發生藍移,共振頻率的藍移是因為隨著待測物質折射率的減小,需要更小等效折射率的多孔金膜來滿足波矢匹配條件.此外,與前文的推測一致,當待測物折射率n發生變化時,介質層最佳厚度會發生相應的改變.通過仿真研究發現,最佳厚度hopt會隨著待測物折射率n的變小而逐漸變小,在覆蓋層為氮氣情況下最佳厚度hopt為3 μm;而在待測物質為汽油、乙醇和液態石蠟(折射率在1.45 附近)的情況下,最佳厚度hopt為7 μm.介質層最佳厚度的減少,是因為隨著共振頻率的藍移,THz 導模在垂直方向上衰減得更快,在棱鏡倏逝波傳播深度有限且一定的情況下需要更小的間隙來滿足耦合條件.通過線性擬合可以得到待測物質為氮氣時,折射率靈敏度高達 13.42 THz/RIU,FOM值為 167.70 RIU-1;而待測物質為汽油、乙醇和液態石蠟時,折射率靈敏度為 3.64 THz/RIU,FOM 值為 145.50 RIU-1.從圖7 仿真結果可以清楚看到,待測物質的折射率n對探測的靈敏度和精度有著很大的影響.隨著待測物質折射率n的減小,該結構的靈敏度會逐漸提高,這是因為小折射率的物質會引起等效折射率更大的變化.但總的來說,導模共振結構對折射率為1-2.3 范圍內的待測物質均保持著高折射率靈敏度和高探測精度的特性.

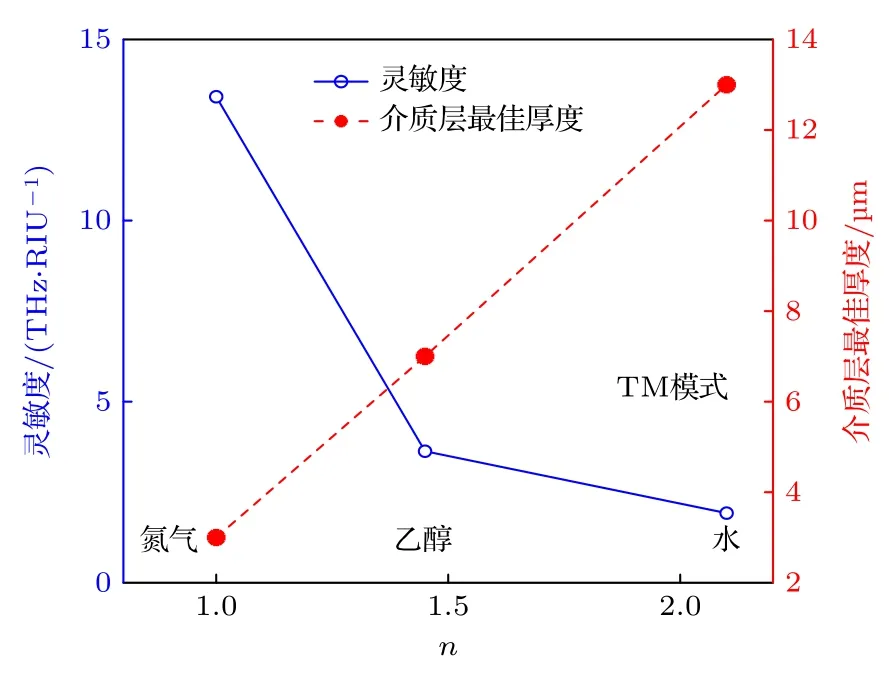
圖7 TM 模式下,不同待測物對應的導模共振結構靈敏度及介質層最佳厚度Fig.7.Sensitivity and optimum thicknesses of dielectric layers of the waveguide resonance structure for different analyses in TM mode.

3.2.2 對生物小分子的探測

除了上述常規應用外,利用多孔金膜富集小分子的能力還能對液體中低濃度的生物小分子進行探測,低濃度的生物小分子意味著它的引入對待測溶液折射率引起的變化很小,使用原有的THz-SPR 傳感器無法對其進行探測.而本文提出的多孔金膜因其孔隙具有富集生物小分子的能力,改變了填充物的比例,即: 吸附生物小分子的體積分數fc不再等于0,因此多孔金膜的等效折射率會發生變化從而引起共振頻率的移動,最終實現對低濃度生物小分子的探測.以酪氨酸為例進行研究,酪氨酸是人體必需的氨基酸之一,且易溶于水和乙醇,在THz波段下其折射率為1.507[38].分別使用TM和TE 模式對吸附體積分數fc=0,0.05,0.10,0.15和0.20 的酪氨酸進行仿真,得到的共振曲線如圖8(a)和圖8(b)所示.從圖8(a)和圖8(b)可清楚地看到,隨著吸附小分子體積分數fc的增大,共振頻率發生藍移,通過線性擬合可以得到如圖8(c)所示的體積分數fc-共振頻率fr的關系.在TM 模式下,導模共振結構靈敏度為 0.81 THz/單位體積分數,而在TE 模式下,該結構靈敏度為 1.18 THz/單位體積分數,從圖8(c)可以明顯看出,TE 模式較TM 模式在探測低濃度酪氨酸小分子方面具有更高的靈敏度.與探測純物質時線性擬合得到的負斜率不同,探測酪氨酸時擬合得到的正斜率是因為酪氨酸的折射率低于水的折射率,當多孔金吸附酪氨酸之后,等效折射率nm會下降,所以會導致共振頻率藍移.研究結果驗證了本文引入的多孔金膜可以對低濃度生物小分子進行檢測的猜想,并且具有較高的探測靈敏度.此外,利用該導模共振結構實時檢測和原位探測的特點,可以對生物小分子的富集過程和分子間的反應進行探測,這使得該結構在生化檢測方面有著巨大的應用潛力.

圖8 (a)TM 模式下,在不同體積分數(fc)酪氨酸情況下的頻率-反射率曲線;(b)TE 模式下,在不同體積分數(fc)酪氨酸情況下的頻率-反射率曲線;(c)TM 和TE 情況下,在不同體積分數(fc)酪氨酸情況下,體積分數(fc)與共振頻率(fr)的線性擬合圖Fig.8.(a)Simulated reflectivity spectra for tyrosine in TM mode at different volume fractions(fc);(b)simulated reflectivity spectra for tyrosine in TE mode at different volume fractions(fc);(c)volume fraction-resonance frequency linear fitting curve for tyrosine in TM and TE mode at different volume fractions(fc).

表1 總結了本文提出的多孔金THz 導模共振傳感結構與不同亞波長金屬周期結構THz 傳感結構在結構尺寸和性能參數方面的對比結果,可以看出本文中提到的基于多孔金/介質雙層膜結構的導模共振結構不僅在尺寸上較亞波長金屬周期結構[26,27,37,39]小很多,更便于集成,還對周圍折射率環境變化更為敏感,即具有高靈敏度的特性.該結構的高靈敏度要歸功于多孔金膜的多孔結構及其大孔隙率,這使得待測物質能夠填充到多孔金膜孔隙之中,在此基礎上,利用多孔結構富集小分子的能力,能夠充分利用場增強效應來提高檢測的精度和靈敏度,這在檢測溶液中低濃度生物小分子方面具有很大的應用潛力.此外,本文所提出的導模共振結構還解決了參考文獻[39]中折射率探測范圍小的缺點,從前文的仿真結果可知,該結構對折射率在1-2.3 范圍內的物質均保持著較高的檢測靈敏度和探測精度.同時,待測物折射率n在一定范圍內的變化不會引起反射頻譜FWHM 較大的展寬,可以精確得到共振頻率的變化,無需再引入相位變化.為了簡化仿真過程,本文的所有結果均忽略了待測物對THz 波的吸收作用,實際情況下,對具有吸收THz 波特性的待測物質進行探測時得到的結果會受到較大的影響,在本文中不詳細討論該部分內容.

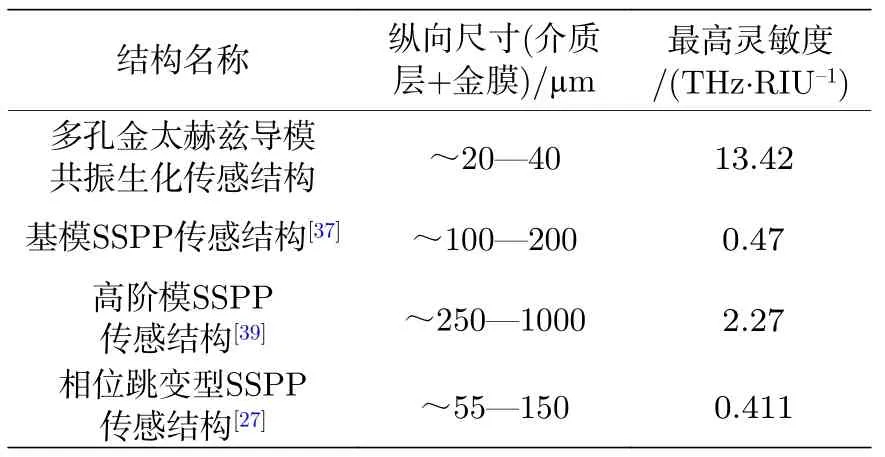
表1 各類基于金膜的太赫茲傳感結構尺寸和性能參數比較Table 1. Au-based terahertz sensing structure dimensions and performance parameters.

4 結論

本文首次提出了基于棱鏡耦合并在非結構化多孔金膜表面激發THz 導模的傳感結構.通過棱鏡產生倏逝波來滿足波矢匹配條件,引入多孔金膜代替原有的亞波長周期金屬結構,多孔金膜不僅可以支持THz 導模傳播,還可以填充待測物質,充分利用局域場增強效應來對物質進行探測.研究發現,棱鏡和多孔金膜之間的介質層厚度和折射率對導模共振結構的性能有很大的影響,在折射率固定的情況下,存在最佳的介質層厚度,即在該厚度下THz 波耦合到THz 導模的效率最高.同時該結構具有寬光譜可調諧的特點,通過改變介質層折射率可以選擇需要的工作波段.在此基礎上,對不同折射率的物質進行了研究,發現該結構對折射率在1-2.3 范圍內的物質均保持著高折射率靈敏度和高探測精度的特性.并且利用多孔金膜比表面積大的特點,在孔隙中富集小分子,通過改變多孔金膜的等效折射率來對溶液中低濃度生物小分子進行探測.除此之外,太赫茲導模存在TE 和TM 兩種模式,因為TE 導模透出多孔金膜的消逝場比TM 導模弱,所以TM模式對純物質的探測更加靈敏,而TE 模式在探測低濃度小分子時更加占優,這不僅拓寬了探測物質的種類,還大大增加了探測的準確性.總的來說,本文引入的多孔金膜打破了傳統太赫茲結構材料種類的束縛,不僅可以將待測物填充到孔隙中,還能對生物小分子進行吸附,增大待測物與THz導模場的作用范圍,從而提高了檢測的靈敏度和精度,這使得該導模共振結構在氣體和液體檢測領域有著巨大的應用前景.