計及暫態模式切換下垂控制逆變器故障下同步穩定分析

馬堰泓，付立軍，胡祺，王光宇，劉陳瑞揚

(海軍工程大學 艦船綜合電力技術國防科技重點實驗室，湖北 武漢 430033)

0 引 言

近年來，風力發電、光伏發電等可再生能源發電技術得到了快速發展，分布式電源大規模接入，使得現代電力系統中傳統的同步發電機所占比例不斷降低，非同步機電源所占比例則逐步增加，而大多數非同步機電源均通過逆變器接口接入大電網[1]。

逆變器的控制方式可分為多種，例如虛擬同步機控制[2]、基于鎖相環的控制方式[3]和下垂控制等。相比其他控制方式而言，下垂控制具有結構簡單、安裝維修便捷、易于控制、系統擴容方便、成本低等優勢[4-5]。

對于并網或孤島運行的下垂控制逆變器，頻率同步是維持有功功率穩定的必要條件。與傳統同步電機具有旋轉質量塊不同[6]，下垂控制的逆變器屬于靜態功率變換裝置，不存在同步電機的“功角”搖擺過程[7-8]，應把經典定義中表征電機受到擾動后與電網保持同步能力的暫態穩定性擴展為同步穩定性[9-11]，依據擾動大小可分為小擾動(靜態)與大擾動(暫態)兩類[12]。

其中，小擾動下的穩定性可在時域或復頻域線性化分析，已初步形成理論體系[13]；而大擾動同步穩定性只能通過時域分析，無法對擾動前平衡點進行線性化處理，分析方法更加復雜，是目前學術研究的熱點。對此，文獻[14]針對大擾動對交流微電網安全運行產生影響的問題，分別從微電網電流特性與穩定運行特性兩個角度進行了分析，但僅僅只是對國內外研究基礎的概括與總結，并沒有提出具體的控制策略；文獻[15]指出，由于電力電子設備的弱應力承受性，在大擾動下逆變器存在因電流過大被燒毀的風險，但并沒有對如何限制過電流進行深入分析；文獻[16]通過在下垂控制的逆變器系統中添加電流限制，使得大擾動下逆變器的輸出電流飽和，逆變電源由電壓源切換為電流源，但并沒有對暫態切換過程進行深入分析。因此，含有電流限幅的逆變器同步穩定性分析方法有待提出。

能量函數法是評估電力系統暫態穩定性最常用的方法之一，而Lyapunov暫態能量函數法能快速分析微電網系統在預想大擾動下的暫態穩定度[17]。目前，基于Lyapunov能量函數的方法，如波波夫絕對穩定性準則[18]、散耗系統理論[19]、基于T-S模糊模型的方法[20]等等，均已被用于評估逆變器的同步穩定性。文獻[21]利用Lyapunov直接法構建了單相逆變器的能量函數，但該方法存在一定的局限性，并未考慮電流限幅對逆變器同步穩定性的影響。

為此，文章對基于下垂控制的逆變電源開展研究。首先建立下垂控制逆變器同步動態動力學模型，分析以電網電壓驟降為例的電網故障下，電壓源/電流源暫態模式切換對等效功角曲線的影響；然后利用Lyapunov直接法分析電壓驟降對系統吸引域的影響，并通過等面積法分析在電流飽和與不飽和情況下系統的同步穩定性，仿真驗證分析的正確性；最后，提出一種基于切換有功與無功控制方式的優化控制策略，理論分析該策略的可行性，仿真驗證該策略的有效性。

1 系統結構

下垂控制的基本控制原理主要是通過模擬同步發電機的頻率和電壓調節特性，從而達到對微電源更加方便有效的控制，實現有功功率和無功功率在并聯逆變器之間的平均分配。

基于下垂控制的三相電壓源型逆變器的拓撲圖如圖1所示。逆變器采用旋轉坐標系下的矢量控制，控制結構可分為三層。最外層為有功調頻、無功調壓下垂控制，有功調頻下垂控制通過結合輸出有功功率及額定角頻率得出角頻率參考值，無功調壓下垂控制通過結合輸出無功功率及額定電壓得到電壓參考值，用于多逆變器間并聯功率均分。中層的dq軸電壓控制用以調節輸出電壓跟隨指令值，其檢測dq軸電壓反饋與指令值的偏差，通過PI控制器調節輸出電流指令，驅動電壓反饋跟隨電壓指令，防止過流，往往加限幅值。內層的dq軸電流控制用以調節輸出電流跟隨指令值，其檢測dq軸電流反饋與指令值的偏差，通過PI控制器調節輸出電壓，驅動電流反饋跟隨電流指令，并產生電壓調制波，通過PWM模塊以驅動半導體開關。

值得注意的是該級聯控制結構下，為保證逆變器動態響應特性與穩定性，功率下垂環、電壓環、電流環三環控制的響應時間有所不同，一般情況下電流環控制的響應速度快于電壓環控制，而由于在功率下垂環控制中往往會添加低通濾波，所以功率控制環響應速度最慢，時間最長。針對系統同步穩定問題，主要與下垂控制相關，因此可重點關注下垂控制動態影響，電壓環與電流環的響應時間可暫時忽略不計。

由于逆變器的弱應力承受性，為保證故障等大擾動下不過流，電流指令往往進行飽和限幅設計，使得限幅前dq電流指令由dq電壓控制調節，限幅后dq電流指令由限幅值決定。下垂控制逆變器常采用基于d軸優先的電流參考限制策略，這種策略描述為：

(1)

(2)

根據式(1)，將電流飽和模式定義為逆變器輸出電流幅值達到Imax并受電流限制策略限制的場景，而電流不飽和模式定義為逆變器輸出電流幅值小于Imax的場景。

綜上所述，由于電流指令飽和限幅，下垂控制逆變器存在電壓源/電流源暫態模式切換過程。系統正常工作時，逆變電源可等效為串聯輸出阻抗的受控電壓源。由于逆變器承受過壓過流能力較弱，故障下逆變器可能會進入電流飽和模式，這使得電流環失去控制，導致逆變電源由電壓源切換為電流源，如圖2所示。這種電壓源/電流源暫態模式切換的情況，導致逆變電源的同步穩定問題分析復雜。

2 同步穩定性分析模型

下垂控制逆變器采用有功調頻、無功調壓下垂控制策略，即：

(3)

其中：V0為無功-電壓下垂控制的電壓給定值；Pref和Qref分別為逆變器的有功功率與無功功率的給定值；PE和QE分別為逆變器的輸出有功功率和無功功率；Kp和Kq分別為有功-頻率和無功-電壓下垂控制系數；ω為逆變器的角頻率參考值；ω0為無窮大電網的角頻率、即額定角頻率。

為濾除高頻擾動，通常對功率檢測值進行低通濾波，表達式為

(4)

其中：濾波后逆變器的輸出有功功率為Pf；T為低通濾波時間常數。

結合式(3)和式(4)，有功調頻下垂控制動態可表示為

(5)

基于式(5)可得

(6)

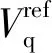
(7)

其中：XΣ表示LCL濾波器電網側阻抗與線路阻抗之和；U表示電網電壓的大小；V表示逆變器輸出電壓的大小。

故障下，逆變器輸出電流變為飽和，逆變電源由電壓源切換為電流源，基于d軸優先級的電流參考限制策略，當逆變電源切換為電流源后，電流幅值由限幅值決定，相位定位于d軸。暫態飽和切換的向量圖如圖3所示。

因此，電流飽和時逆變器有功功率PE可計算為

PE=ImaxUcosδ=Psmcosδ。

(8)

其中：Imax表示電流限幅值；U表示電網電壓的大小。根據式(5)、式(7)和式(8)可繪制出下垂控制的逆變器中有功-頻率控制的動態響應，如圖4所示。

3 同步穩定機理研究

3.1 基于Lyapunov直接法構造能量函數

根據圖4可以得到下垂控制的逆變器系統在電流不飽情況下的狀態方程為

(9)

結合式(9)和式(6)可得

(10)

基于式(7)，通過將PE賦為Pref可得逆變器在故障前的穩定平衡點δs表達式為

(11)

為了采用Lyapunov直接法構造能量函數，需要將穩定平衡點從(δs，ω0)平移到(0，0)，定義：

(12)

因此，狀態方程(10)可以寫作：

(13)

對其構造Lyapunov能量函數為

(14)

在電網電壓驟降這類電網故障情況出現后，由于逆變電源存在從電壓源切換為電流源、電流非飽和切換為飽和的過程，因此不同時刻的穩定平衡點δs、不穩定平衡點δu也將發生改變。平衡點的改變過程將在3.2節具體分析。

從數學角度講，構造Lyapunov能量函數的目的在于研究在故障清除時系統的狀態變量是否在吸引域內，從而判斷系統能否回到穩定狀態。因此需要計算不同時刻的臨界能量。臨界能量Vcr定義為系統處于不穩定平衡點時，以穩定平衡點δs為參考點系統所具有的勢能。

首先通過系統功角特性曲線得到故障發生后系統的穩定平衡點與不穩定平衡點，分別用(δs，ω0)和(δu，ω0)表示，然后將不穩定平衡點(δu，ω0)代入式(14)即可計算出臨界能量Vcr。根據上述步驟，可以得到臨界能量函數表達式為

Vcr=V(δu,ωg)。

(15)

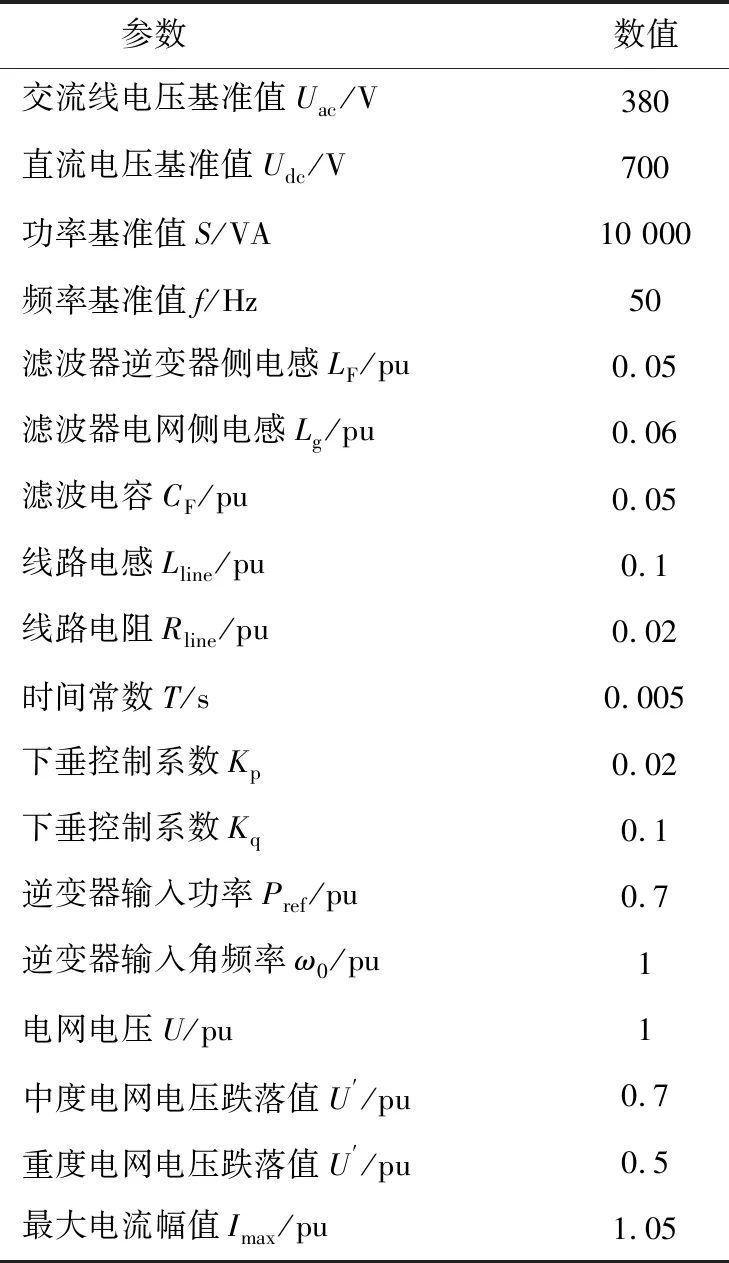
故障發生后，通過計算故障清除時系統的角頻率ωc與功角δc，將其帶入式(14)中可以得到故障后系統的總能量Vc。當Vc

考慮到電壓源/電流源暫態模式切換過程，在故障發生時，逆變器輸出有功功率表達式由式(7)切換為式(8)，能量函數表達式(14)將會變為

ImaxU(sin(x1+δs)-sinδs)+

(16)

3.2 系統同步穩定分析

在3.1節的分析中，逆變器功角變化率與輸出有功功率之間的關系式如式(10)所示。直接繪制系統功角特性曲線，利用能量函數法來對系統的穩定性進行分析。

由式(7)和式(8)繪制出下垂控制逆變器在電流飽和與非飽和情況下的功角特性曲線，如圖5所示。

結合所建模型以及動力學方程(10)可知，逆變器的輸出有功功率PE與功率給定值Pref的偏差可以驅動逆變器角頻率的加速或減速。因此，在功率給定值Pref下方的區域可定義為加速區域，功率給定值Pref上方的區域可定義為減速區域。如果系統工作點在經過加速區域和減速區域后沒有出現不穩定性，那么系統就會穩定在一個平衡點，這個平衡點就是功角特性曲線與功率給定值的交點。

由圖5可知，電網電壓U跌落程度決定了故障后的飽和功角特性曲線是否與功率給定值Pref相交。因此可定義中度電網電壓跌落的情況為：飽和功角特性曲線與功率給定值存在交點；重度跌落的情況則沒有交點。可描述為：

(17)

下文將分兩種情況對電網故障時逆變器的同步穩定性進行分析。

3.2.1 重度電網故障的情況

在重度電網故障的情況下，電網電壓幅值從U突降為U′時，逆變器的功角特性曲線如圖6所示。其中，P(1)與P(2)分別為電壓驟降前后飽和功角特性曲線。當功率給定為Pref，且系統處于穩態時，工作點穩定在A點。

當電壓驟降發生時，逆變器進入電流飽和模式，工作點從A點突變至A′點。A′點的輸出有功功率PE小于Pref，此時系統進入加速區域，逆變器功角沿著飽和功角特性曲線P(2)持續增大。由圖6可知，故障期間系統不存在平衡點，因此也就無法達到平衡狀態。

設E′點為故障恢復點，故障恢復后，工作點由E′點突變至E點，故障恢復時的功角特性曲線如圖7所示。

故障切除過程中，系統的加速面積是S1，減速面積是S2。加減速面積的表達式如下：

(18)

假設在F點切除故障時，加減速面積相等，即S1=S2，稱F點為臨界清除點。通過臨界清除點可將故障切除分為3種不同的情況，如圖7所示，下文將分別進行分析。

1)當δE≤δF時，故障切除后逆變器的輸出有功功率PE>Pref，系統進入減速區域，逆變器的功角沿著飽和功角特性曲線P(1)減小。

此時系統的加速面積S1小于減速面積S2，由等面積法則可知，系統最終將會穩定在A點。

2)當δF<δE≤δD時，故障切除后逆變器輸出有功功率PE仍然大于功率給定值Pref。但由于δE>δF，導致系統的加速面積S1大于減速面積S2，因此系統不會穩定在A點。逆變器的功角會沿著飽和功角特性曲線P(1)持續減小，最終穩定工作在C點。值得注意的是，C點不是理想的工作點，因為C點處電流仍然飽和，電壓仍然不受控制，在工程實踐中要盡可能避免。

上述兩種情況，由于切除時間的不同，導致故障切除時系統的能量發生變化，使得系統穩定平衡點由A點切換到C點。

根據Lyapunov能量函數(14)可計算出該過程的吸引域的變化情況，如圖8所示。其中，Vcr1和Vcr2分別表示故障修復后回到平衡點A點和C點吸引域的臨界能量。由圖可知，故障切除時系統運行點回到穩定平衡點A點要比回到C點更加困難。

圖9用Lyapunov直接法展示了故障切除時系統能量與臨界能量的對比。臨界能量Vcr1和Vcr2與圖8中的曲線一致。由圖9可知，故障發生后，系統總能量隨時間增加。當能量超過Vcr1后，系統的穩定平衡點由A點切換到C點。若故障清除時系統的總能量低于臨界能量，則系統能保持同步穩定。反之，若故障切除時系統的能量超過了臨界能量，則無法保持穩定。

根據表1的數據構建仿真模型，首先計算臨界清除角δF。由式(18)可得，當S1=S2時，δF=0.69 rad。

仿真結果如圖10所示，其中Tc表示從故障切除時間。根據仿真結果可知，當Tc=0.48 s時，對應逆變器的功角δ=0.681 rad，滿足δE<δF條件，系統能夠回到穩定平衡點A點。當Tc=0.49 s時，逆變器的功角δ=0.698 rad，滿足δE>δF，加速面積大于減速面積，系統的工作點最終穩定在C點。因此，仿真結果與理論分析一致，證明了同步穩定分析的正確性。

表1 仿真模型的參數

3)當δE>δD時，逆變器的輸出有功功率PE

在MATLAB/Simulink中，用仿真驗證上述Lyapunov直接法的正確性，結果如圖11所示。當故障在0.45 s被清除時，功角δ能回到穩定平衡點A點。當故障在0.55 s被清除時，功角δ能回到平衡點C點。當故障在0.65 s被清除時，系統狀態變量發散，無法達到平衡點。仿真結果與Lyapunov直接法的結論相一致。

3.2.2 中度電網故障的情況

中度電網故障下系統的的功角特性曲線如圖12所示，當功率給定為Pref，且當系統處于穩態時，工作點穩定在A點，其功角為δA。

在中度電網電壓跌落的情況下，逆變電源進入電流飽和模式，由電壓源切換為電流源。系統的工作點從A點突變至A′點，且A′點的輸出有功功率PE>Pref，由前文的分析可知，此時系統處于減速區域，逆變器的功角將減小，沿著飽和功角特性曲線P(2)移動，最終到達穩定平衡點C′。

故障清除后，系統的工作點將從C′點跳變到C″點。由于C″點的有功功率輸出仍然大于Pref，系統仍處于減速區域，逆變器的功角將繼續減小并達到飽和功角特性曲線P(1)上的穩定平衡點C。

故障清除的過程，使得系統的穩定平衡點發生切換，導致故障切除前后臨界能量發生變化。整個過程的能量與臨界能量對比如圖13所示，其中Vcr1和Vcr2分別表示故障切除前后的臨界能量。由圖13可知，故障發生后，系統的能量突增，但沒有超過臨界能量Vcr1，隨后隨時間漸漸降低至0，由此判斷系統能保持同步穩定。故障切除后，系統的能量遠低于臨界能量Vcr2，因此仍然能保持穩定。因此，故障切除時間并不會對系統保持同步穩定產生影響。

為了驗證上述理論分析，在MATLAB/Simulink平臺構建了如圖1所示的仿真模型，仿真模型參數配置如表1所示。

仿真結果如圖14所示，逆變器正常運行時，工作點為A點。當電網電壓幅值U從1.0 pu突降至0.8 pu時，逆變器的功角將持續減小，工作點由A點移動至不穩定平衡點C′。故障清除后，系統將穩定在C點運行，無法返回到A點。仿真結果與結論一致，驗證了結論的有效性。

4 提高同步穩定性的優化策略

根據3.2節的分析可知，在電網發生嚴重故障期間，逆變器輸出電流飽和，逆變電源由電壓源切換為電流源。由于此時逆變器輸出有功功率PE恒小于Pref，系統處于加速區域，功角持續增大，無法達到平衡狀態，逆變器發生同步失穩。

3.2節通過Lyapunov直接法構造系統的能量函數，詳細分析了故障切除時間對系統同步穩定性的影響。然而，在某些特定的情況下，無法及時切除電網發生的故障，需要采用一些特殊的控制方式使系統保持同步穩定。

針對以上問題，提出一種暫態同步控制策略，在逆變器輸出電流飽和階段，通過將有功調頻控制切換為無功調頻控制，使故障期間逆變器功角穩定，以此增強系統同步穩定性。

4.1 優化控制策略的描述

圖1中線路動態方程為：

(19)

其中：XΣ為網側濾波電抗與線路電抗之和；LΣ為對應的電感值；RΣ為對應的電阻值，在電路呈感性的條件下，RΣ可忽略不計，并且LΣ≈XΣ。

逆變器輸出功率計算方程為：

(20)

電流飽和的情況下，Id=Imax，Iq=0代入式(19)、式(20)可得：

(21)

由式(21)可知，在電流飽和的情況下，逆變器輸出無功功率與功角存在一定的數學關系，由此繪制無功功角特性曲線如圖15所示。

由圖15可知，由于下垂控制中無功-電壓下垂部分功率給定值Qref的存在，逆變器穩定工作時，系統的無功工作點穩定在C點。

在重度電壓跌落的情況下，逆變電源由電壓源切換為電流源，系統發生同步失穩，功角持續增大。無功工作點由C點突變至C′點，且無功功率也會隨功角的增大而呈正弦規律振蕩，無法保持穩定。

因此，提出一種優化控制策略，具體描述為：故障發生后，在逆變器電流飽和階段，將有功調頻控制切換為無功調頻控制，通過給定無功功率限制QL，使逆變器的功角保持穩定，從而使得有功功率不會發生同步失穩。這種控制策略的原理與控制方式如下式和下圖所示：

(22)

根據式(22)繪制帶有優化控制策略的逆變器飽和功角曲線如圖17所示。

由圖17可知，故障發生后，逆變器發生飽和切換，進入電流飽和模式，有功工作點由穩定平衡點A′點突變為A′點。由于優化策略的存在，逆變器轉為無功功率控制，工作點切換為無功功角特性曲線上的C′點，隨后穩定在無功功角特性曲線與無功功率限制QL的交點處，即圖中的C″點。由于此時逆變器的功角已趨于穩定，不再變化，因此對應的輸出有功功率同樣能維持穩定，不發生振蕩。有功功率工作點穩定在圖中A″點。

4.2 仿真驗證

為了驗證該策略對提高系統同步穩定性的作用，在MATLAB/Simulink平臺構建仿真模型，仿真參數見表1，其中QL=0.5。

仿真結果如圖18所示。由圖可知，在未添加優化控制的情況下，電網發生故障的瞬間，有功與無功功率均發生突變，并沿著功角特性曲線變化，與前文分析一致。

添加優化控制后的功角特性曲線如圖19所示。由圖可知，在電網故障后，功率控制方式發生切換，由于添加了無功功率限制QL，使得逆變器輸出有功功率與無功功率能保持在一個定值，功角不再發生變化，保持穩定。

綜上所述，沒有采用優化策略的系統，在電網故障時發生了暫態功角失穩，由于此時不存在平衡點，系統無法保持穩定；而采用優化控制策略后的逆變器，在電網故障后，能使逆變器輸出有功功率與無功功率維持恒定。因此，該優化控制策略能提高下垂控制逆變器的功角穩定性。

5 結 論

電網故障下，三相電壓源型逆變電源電流指令飽和限幅使得其會發生電壓源/電流源模式切換過程，給其同步穩定性帶來考驗。計及該暫態模式切換影響，首先建立了下垂控制逆變器同步動態動力學模型，分析了電壓源/電流源模式切換對其同步動態的影響。進而運用Lyapunov直接法建立了電壓源/電流源兩種運行模式下系統的暫態能量函數，從加減速面積和系統能量變化的角度分析了電網故障下系統同步穩定性及影響因素，并提出了一種基于功率改進控制的優化控制策略以增強同步穩定性，得到結論如下：

1)重度電網故障的情況下，下垂控制的逆變器故障期間不存在平衡點，發生同步失穩，而根據故障切除時間的不同，切除后系統存在3種不同的工作狀態，并且切除時間越長越難保持穩定。

2)中度電網故障的情況下，故障期間系統仍存在穩定平衡點，并且無論何時切除故障，系統總會工作在電流飽和的穩定平衡點。

3)提出的基于功率改進控制的優化控制策略可以解決采用下垂的控制逆變器在電網嚴重故障下失穩的問題，有效提高系統暫態同步穩定性。